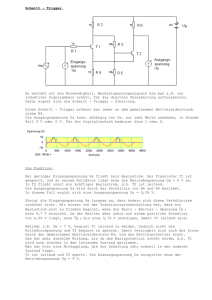
Messung nichtsinusförmiger Größen

Institut für Energiesysteme, Energieeffizienz und
Energiewirtschaft
Prof. Dr.-Ing. Christian Rehtanz
Praktikumsversuch
V211
Messung nichtsinusförmiger
Größen
Stand: 06.05.2015
Inhaltsverzeichnis
Inhaltsverzeichnis ....................................................................................................................... 2
1
Versuchsthematik ................................................................................................................ 3
2
Theoretische Grundlagen .................................................................................................... 3
2.1
Kenngrößen für Wechselstrom- und Mischsignale ..................................................... 3
2.1.1
Linearer Mittelwert .............................................................................................. 4
2.1.2
Effektivwert .......................................................................................................... 4
2.1.3
Crest-Faktor .......................................................................................................... 5
2.1.4
Formfaktor ............................................................................................................ 5
2.1.5
Gleichrichtwert ..................................................................................................... 6
2.2
Schaltungstechnische Realisierung.............................................................................. 7
2.2.1
Diode, Thyristor, Triac ......................................................................................... 7
2.2.2
Operationsverstärker ............................................................................................ 9
2.2.3
Zweiweggleichrichtung mit Diodenbrücke (Graetz-Brücke) ............................. 11
2.2.4
Wechselstromsteller mit Phasenanschnittsteuerung........................................... 11
2.2.5
Magnetisierungsstrom eines Transformators im Leerlauf ................................. 13
2.2.6
Spitzenwertgleichrichtung .................................................................................. 14
2.2.7
Präzisions-Spitzenwertgleichrichtung ................................................................ 16
2.3
Versuchsausstattung .................................................................................................. 16
2.3.1
Bauteile............................................................................................................... 17
2.3.2
Trenn- und Regeltransformator .......................................................................... 18
2.3.3
Oszilloskop ......................................................................................................... 18
2.3.4
Multimeter .......................................................................................................... 19
3
Verständnisfragen ............................................................................................................. 20
4
Versuchsdurchführung ...................................................................................................... 21
5
4.1
Grundeinstellungen .................................................................................................... 21
4.2
Brückengleichrichter mit ohmscher Last ................................................................... 21
4.3
Wechselstromsteller mit Phasenanschnittsteuerung und ohmscher Last .................. 27
4.4
Transformator im Leerlauf ........................................................................................ 30
4.5
Einfacher Spitzenwertgleichrichter ........................................................................... 31
4.6
Präzisions-Spitzenwertgleichrichter mit Operationsverstärker ................................. 35
Anmerkung zur Ausarbeitung (Wirt-Ings.) DIGITAL als PDF an jonas.von-haebler@tu-
dortmund.de.............................................................................................................................. 37
2
1 Versuchsthematik
In der Praxis treten häufig Spannungen und Ströme auf die nicht einer idealen Form
entsprechen. Ideale sinusförmige oder gleichgerichtete Spannungen und Ströme können zum
Beispiel durch nichtlineare Bauteile stark in ihrer Form verändert werden. Des Weiteren kommt
es vor, dass sich Wechsel‐ und Gleichanteile überlagern und so Mischsignale entstehen. In dem
Versuch werden die wichtigsten Kenngrößen der Signale erläutert und Schaltungen vorgestellt
um sie zu messen. Neben grundlegenden Schaltungen aus der Praxis zur Messung des
Effektivwertes von sinusförmigen Signalen, werden auch Schaltungen zur Bestimmung von
Spitzenwerten beliebiger Signale analysiert. Im weiteren Verlauf wird auch gezeigt wie man
durch den Einsatz von Operationsverstärkern in Präzisionsschaltungen Verbesserungen bei
Störungen durch nichtlineare Bauteile erreichen kann.
2 Theoretische Grundlagen
2.1 Kenngrößen für Wechselstrom- und Mischsignale
In der Fachliteratur und der Versuchsanleitung werden für die Strom‐ und Spannungswerte der
verschiedenen Signalarten zur genauen Differenzierung unterschiedliche Symbole verwendet. In
Tabelle 2.1 werden die hier verwendeten Symbole beschrieben.
Symbole für
Sinusförmige Signale
Nichtsinusförmige
Wechselstromsignale
Mischsignale
Momentanwerte
𝑢(𝑡), 𝑖(𝑡)
𝑢(𝑡), 𝑖(𝑡)
𝑢(𝑡), 𝑖(𝑡)
Scheitelwerte
̂, 𝐼̂
𝑈
̂, 𝐼̂
𝑈
̂, 𝐼̂
𝑈
Mittelwerte
-
-
Effektivwerte
𝑈, 𝐼
𝑈𝑒𝑓𝑓 , 𝐼𝑒𝑓𝑓
𝑈𝑒𝑓𝑓 , 𝐼𝑒𝑓𝑓
Gleichrichtwerte
̅̅̅̅
̅̅̅
|𝑢|, |𝑖|
̅̅̅̅
̅̅̅
|𝑢|, |𝑖|
̅̅̅̅
̅̅̅
|𝑢|, |𝑖|
Tabelle 2.1: Syntax
Momentanwerte sind die Augenblickswerte 𝑢(𝑡) bzw. 𝑖(𝑡) des Verlaufes von Spannung bzw.
Strom. Scheitelwerte sind die maximalen bzw. minimalen Werte und werden auch Spitzenwerte
oder Amplitude genannt.
Nichtsinusförmige Wechselstromsignale haben beliebige andere periodische Verläufe, enthalten
jedoch in jeder Periode gleich viele positive wie negative Anteile. Ihr Mittelwert (siehe unten) ist
Null.
3
Mischsignale haben beliebige Verläufe, aber sie besitzen einen Gleichstrom‐ bzw.
Gleichspannungsanteil. Ihr Mittelwert ist ungleich Null.
Abbildung 2.1: Augenblickswert, linearer Mittelwert, Gleichrichtwert und Spitzenwert a) einer sinusförmigen
Spannung; b) einer Mischspannung
2.1.1 Linearer Mittelwert
Der lineare Mittelwert, arithmetische Mittelwert oder die Gleichstromkomponente einer
beliebigen periodischen Spannung u(t) ist definiert als:
1 𝑇
𝑢̅ = ∫ 𝑢(𝑡)𝑑𝑡
𝑇 0
[2.1]
2.1.2 Effektivwert
Definition im Zeitbereich: Eine Definition des Effektivwertes über den zeitlichen Verlauf des
Signales ist:
1 𝑇
𝑢𝑒𝑓𝑓 = √𝑢̅² = √ ∫ 𝑢² 𝑑𝑡
𝑇 0
[2.2]
̂ ∙ sin(𝜔𝑡) gilt mit der Umformung
Für sinusförmige Größen 𝑢 = 𝑈
1
(sin(𝑥))2 = (1 − 𝑐𝑜𝑠(2𝑥))
2
und 𝜔 = 1
[2.3]
̂2 1
̂
1 2𝜋
𝑈
1
2𝜋
𝑈
̂ sin(𝜔𝑡))2 𝑑(𝑡) = √ [ 𝑡 −
𝑈𝑒𝑓𝑓 = √ ∫ (𝑈
sin(2𝜔𝑡)]
=
2𝜋 0
2𝜋 2
4𝜔
0
√2
[2.4]
Definition im Frequenzbereich (Bildbereich): Ein anderer Weg zur Bestimmung des
Effektivwerts geht von seinem Frequenzspektrum aus. Mit Hilfe der Fourieranalyse lässt sich
jede
beliebige
(auch
nichtsinusförmige),
periodische
Spannung
in
die
Gleichspannungskomponente 𝑢̅ und in eine Reihe von sinusförmigen Spannungen
4
𝑢1 , 𝑢2 … 𝑢𝑘 ,
den
sogenannten
Harmonischen,
Fourier‐,
Spektral‐
oder
Wechselspannungskomponenten, zerlegen:
∞
̂𝑘 (𝑘𝜔𝑡 + 𝜑𝑘 )
𝑢 = 𝑢̅ + ∑ 𝑈
[2.5]
𝑘=0
Die erste Wechselspannungskomponente (k=1) wird als Grundschwingung oder Grundwelle
bezeichnet und die restlichen Wechselspannungskomponenten werden Oberschwingungen oder
Harmonische genannt. Die Oberschwingungen 𝑢𝑘>1 besitzen die k‐fache Frequenz der
Grundschwingung des periodischen Signals.
Wenn ein Messsignal lückenlos alle Fourierkomponenten bis zur Ordnungszahl n, inklusive der
Gleichspannungskomponente, enthält, ergibt sich der echte Effektivwert dieses Signals als
quadratisches Mittel der Fourierkomponenten:
𝑈𝑒𝑓𝑓 = √𝑢̅ 2 + 𝑈12 + 𝑈22 + ⋯ + 𝑈𝑛2
[2.6]
Bei Signalen, die nur eine Gleichspannungs- und eine Wechselspannungskomponente
enthalten entspricht der Effektivwert des gesamten Signals:
̅ 𝟐 + 𝑼𝟐𝒘𝒆𝒇𝒇
𝑼𝒆𝒇𝒇 = √𝒖
[2.7]
2.1.3 Crest-Faktor
Der Crest‐Faktor CF oder Scheitelwertfaktor wird für ein beliebiges Signal definiert als:
𝐶𝐹 =
̂
𝑆𝑐ℎ𝑒𝑖𝑡𝑒𝑙𝑤𝑒𝑟𝑡
𝑈
=
𝐸𝑓𝑓𝑒𝑘𝑡𝑖𝑣𝑤𝑒𝑟𝑡 𝑈𝑒𝑓𝑓
[2.8]
Bei sinusförmigen Größen hat der Crest-Faktor den bekannten Wert √2.
2.1.4 Formfaktor
Der Formfaktor wird für ein beliebiges Signal definiert als:
𝐹=
𝑈𝑒𝑓𝑓
𝐸𝑓𝑓𝑒𝑘𝑡𝑖𝑣𝑤𝑒𝑟𝑡
=
̅̅̅̅
𝐺𝑙𝑒𝑖𝑐ℎ𝑟𝑖𝑐ℎ𝑡𝑤𝑒𝑟𝑡
|𝑢|
[2.9]
Für eine sinusförmige Spannung ist der Formfaktor:
𝐹=
𝑈
𝜋
=
= 1,11072 ≈ 1,11
̅̅̅̅ 2√2
|𝑢|
Der Effektivwert einer sinusförmigen Spannung lässt sich damit berechnen als:
5
[2.10]
̅̅̅̅ = 1,11|𝑢|
̅̅̅̅
𝑈 = 𝐹|𝑢|
[2.11]
2.1.5 Gleichrichtwert
Den
Gleichrichtwert
oder
Betragsmittelwert
erhält
man,
wenn
vor
einer
Mittelwertberechnung der Betrag der Funktion gebildet wird:
𝑇
̅̅̅̅ = 1 ∫ |𝑢(𝑡)| 𝑑𝑡
|𝑢|
𝑇 0
[2.12]
Bei einer sinusförmigen Spannung erhält man:
̅̅̅̅
|𝑢| =
̂ 𝜋
̂
1 2𝜋
2𝑈
𝑈
𝜋
̂ sin(𝜔𝑡)|𝑑(𝜔𝑡) =
∫ |𝑈
∫ sin(𝜔𝑡) 𝑑(𝜔𝑡) = [−cos(𝜔𝑡)]
2𝜋 0
2𝜋 0
𝜋
0
2
2
̂ = √2𝑈 ≈ 0.9.
= 𝑈
𝜋
𝜋
[2.13]
Der Gleichrichtwert ist eine leicht zu messende Größe. Die erforderliche
Betragsbildung wird bei Messgeräten durch eine Gleichrichtung des Messsignals
erreicht. Die anschließende Mittelwertbildung ergibt sich bei Drehspulinstrumenten
durch die Trägheit des beweglichen Organs, bei digitalen Multimetern durch
elektronische Integriererschaltungen.
Vom Gleichrichtwert ausgegangen, kann man den Effektivwert und den Scheitelwert
von Spannungen mittels des Formfaktors und des Crest-Faktors rechnerisch
bestimmen. Dies ist messtechnisch einfacher zu realisieren als das Quadrieren für eine
echte
Effektivwertmessung
und
wurde
deshalb
früher
bei
Wechselspannungsmessungen oft eingesetzt.
Dieses Verfahren liefert jedoch nur dann korrekte Ergebnisse wenn der richtige Formund Crest-Faktor im Messgerät berücksichtigt wird. Bei AC-Messung wird von einer
reinen Sinusform und den entsprechenden Faktoren ausgegangen, sodass bei einer
nichtsinusförmigen Wechselgröße fehlerhafte Ergebnisse erzielt werden.
6
2.2 Schaltungstechnische Realisierung
2.2.1 Diode, Thyristor, Triac
Diode
Die Diode ist ein Zweischicht‐Halbleiterbauelement, bestehend aus einer n‐leitenden und einer p‐
leitenden Halbleiterschicht. An der Grenze der beiden Schichten, dem sogenannten pn‐Übergang,
herrscht
ein
Ladungsträger‐Konzentrationsunterschied.
Infolge
dieses
Konzentrations-
unterschiedes wandern die Elektronen aus dem n‐ in das p‐Gebiet, die Löcher aus dem p‐ in das n‐
Gebiet. In dem Grenzgebiet treffen Elektronen und Löcher aufeinander und rekombinieren.
Aufgrund dessen verarmt die Schicht an beweglichen Ladungsträgern welche einen Strom bilden
könnten. Diese Schicht, die Sperrschicht, hat folglich einen hohen elektrischen Widerstand. Die
beiden Anschlüsse der Diode heißen Anode an der p‐Schicht und Katode an der n‐Schicht. Der
Aufbau der Diode und das Schaltzeichen sind in Abbildung 2.2 dargestellt.
Abbildung 2.2 Diode – Schaltzeichen und Aufbau
An die Diode kann eine in Größe und Richtung variierende Spannung 𝑈𝐷 angelegt werden, welche
die Diode in einen sperrenden oder leitenden Zustand versetzt. Prinzipiell sind zwei Fälle zu
unterscheiden. Wird der positive Pol der Spannung an den p‐Halbleiter angelegt (Anode) und der
negative an den n‐Halbleiter (Katode), werden die Ladungsträger per Influenz in die Sperrschicht
hineingetrieben, wodurch diese kleiner wird. Der Wiederstand verringert sich sehr stark, sodass die
Diode leitet und somit in Durchlassrichtung betrieben ist. Wird die Spannung entgegengesetzt
angelegt, werden die Ladungsträger der Sperrschicht entzogen und die Diode weist deshalb einen
großen Wiederstand auf. Die Diode wird in Sperrrichtung betrieben. Diese Wirkung der Diode
erinnert an ein Ventil, da sie den Stromfluss in eine Richtung zulässt und in die andere Richtung
blockiert. Diese Ventilwirkung wird in den nachfolgenden Schaltungen z.B. dafür genutzt
Wechselsignale gleichzurichten. Eine besondere und wichtige Eigenschaft der Diode ist, dass sie
7
erst ab einer Bestimmten Spannung in Durchlassrichtung leitend wird. Diese Spannung wird
Durchlassspannung, Durchbruchsspannung, Flussspannung oder Schleusenspannung genannt und
liegt bei Silizium Dioden bei ca. 0,7V und bei Germanium Dioden bei 0,3V. Abbildung 2.3 zeigt
die Kennlinie einer Diode. Die Achsen in positiver Richtung (IF und UF) stellen den Strom bzw.
die Spannung in Durchlassrichtung dar. UF0 bezeichnet hier die Durchlassspannung der Diode. Die
Achsen in negative x und y Richtung (IR und UR) beschreiben das Verhalten der Diode wenn sie
in Sperrrichtung betrieben wird. Der Sperrstrom durch die Diode ist mit IS gekennzeichnet und in
der Grafik in μA und nicht wie der Strom in Durchlassrichtung in mA angegeben.
Abbildung 2.3 Kennlinie einer Diode
Thyristor
Der Thyristor ist ein Halbleiterbauelement mit vier Halbleiterschichten in der Reihenfolge p‐n‐p‐n
und hat demzufolge drei Übergänge der p und n Schichten. Die beiden äußeren Anschlüsse heißen
Anode und Katode und es existiert ein zusätzlicher Anschluss am katodenseitigen p‐Gebiet, die
Steuerelektrode. Der Thyristor verhält sich im Wesentlichen wie eine Diode, bis auf den
Unterschied, dass der Thyristor gesteuert werden kann. Liegt an dem Thyristor, also an der Anode
und Katode, eine positive Spannung an, leitet er solange nicht, bis er gezündet wird. Das Zünden
geschieht über die Steuerelektrode, indem eine Zündspannung an ihr angelegt wird. Ist der Thyristor
einmal in einem leitenden Zustand kann er erst wieder gelöscht werden, wenn der Strom unter einen
bestimmten Wert fällt, dies ist der Haltestrom. Dieser Strom ist relativ klein, sodass er meist zu Null
angenommen werden kann. Bei Wechselsignalen spricht man deshalb auch vom Löschen beim
Nulldurchgang des Stromes. Dadurch, dass der Thyristor innerhalb einer Halbwelle nicht von
8
alleine löscht, ist es für die Zündung ausreichend, wenn Steuer‐ oder Zündspannung die Form eines
kurzen Impulses hat.
Abbildung 2.4 Schaltzeichen Thyristor
Triac
Der Triac setzt sich aus zwei antiparallel geschalteten Thyristoren zusammen. Bei anliegender
Wechselspannung können sowohl der positive als auch der negative Anteil der Spannung verzögert
eingeschaltet werden. Gezündet werden die beiden Thyristoren meist symmetrisch.
Abbildung 2.5 Schaltzeichen Triac
2.2.2 Operationsverstärker
Der Operationsverstärker ist ein Gleichspannungsverstärker in Form von integrierten Schaltungen.
Im Rahmen dieser Versuchsanleitung beschränken wir uns auf das ideale Verhalten eines OP, des
Weiteren wird nur sein Verhalten mit äußerer Beschaltung betrachtet und nicht sein innerer Aufbau.
Der OP besitzt zwei Eingänge und einen Ausgang jeweils bezogen auf die Masse, siehe Abbildung
2.6. Der Eingang der mit + gekennzeichnet ist stellt den nicht invertierenden und der mit –
gekennzeichnete den invertierenden Eingang dar. Die Spannung 𝑈𝐷 = 𝑈+ − 𝑈− ist die
Differenzspannung. Sie wird mit dem Verstärkungsfaktor 𝑣0 (Leerlaufverstärkung bei offenem
Ausgang) auf die Ausgangsspannung 𝑈𝐴 = 𝑈𝐷 ∙ 𝑣0 verstärkt. Im Idealfall hat der OP einen sehr
großen Verstärkungsfaktor im Bereich 𝑣0 ≈ 104 − 106 . Für die Differenzspannung ergibt sich also
𝑈𝐷 =
𝑈𝐴⁄
−4
−6
𝑣0 ≈ 10 − 10 ≈ 0 und folglich auch 𝑖0 ≈0.
9
Des Weiteren zeichnen sich ideale OP durch einen unendlich großen Eingangswiderstand und einen
Ausgangswiderstand von Null aus.
Abbildung 2.6 Schaltzeichen Operationsverstärker
Die beiden Anschlüsse +𝑈𝐵 und −𝑈𝐵 dienen der Spannungsversorgung des OP und haben
keinen Einfluss auf die Wirkung der äußeren Beschaltung. Fast alle Schaltungen mit OP weisen
eine sogenannte Rückkopplung auf. Bei Schaltungen mit Rückkopplung wird ein Teil der
Ausgangsspannung wieder auf den Eingang zurückgeführt. Für unsere Zwecke ist die
Beschaltung als Spannungsfolger oder Impedanzwandler von Bedeutung (siehe Abbildung 2.7)
Abbildung 2.7: Spannungfolger
Da der Ausgang mit dem Eingang verbunden ist gilt immer 𝑈𝐴 = 𝑈𝐸 , die Ausgangsspannung
folgt also der Eingangsspannung (Spannungsfolger). Eventuelle Spannungsabfälle in dem
10
Rückkopplungszweig werden so ausgeglichen und es steht immer die gesamte
Eingangsspannung am Ausgang zu Verfügung.
2.2.3 Zweiweggleichrichtung mit Diodenbrücke (Graetz-Brücke)
Abbildung 2.8: Zweiweggleichrichtung mit Greatz‐Brücke a) Messschaltung; b) Zeitvariable Größen Simuliert
mit „NGSPICE“ (*berechnete Größen)
Während der positiven Halbwelle der Spannung fließt der Strom durch die Dioden D1 und D3
und während der negativen Halbwelle durch die Dioden D2 und D4. In beiden Fällen hat der
Strom durch das Messgerät dieselbe Richtung.
2.2.4 Wechselstromsteller mit Phasenanschnittsteuerung
Abbildung 2.9: Wechselstromsteller als Lampendimmer.
11
Abbildung 2.10: Idealisierte zeitvariable Größen bei der Lampendimmerschaltung (∝=45°)
Wechselstromsteller dienen zur Steuerung großer Leistungen in Wechselstromkreisen. Bei der
Phasenanschnittsteuerung wird der Laststrom nur für einen Teil der Dauer einer
Wechselspannungshalbwelle eingeschaltet. Als Schalter dient ein Triac, ein Halbleiterbauteil,
das zwei antiparallel geschalteten Thyristoren entspricht und einen Stromfluss in beliebiger
Richtung zulässt. Durch einen kurzen Zündimpuls kann es in den eingeschalteten Zustand
versetzt werden, das Ausschalten geschieht von alleine beim Nulldurchgang des Laststromes.
Der Zündimpulsgenerator des Wechselstromstellers, der als Dimmerschaltung eingesetzt wird,
liefert nach jedem Nulldurchgang der Speisespannung einen zeitlich verzögerbaren Zündimpuls
𝑢𝑧 für den Triac.
Der Steuerwinkel oder Zündwinkel ∝ (siehe Abbildung 2.10) kann mit einem Potentiometer
von Hand eingestellt werden. Mit dem Zündimpuls wird der im Schaltbetrieb arbeitende Triac
in den leitenden Zustand versetzt, so dass durch die Glühlampe für die Dauer ∝𝐶 Strom fließen
kann. Durch Verstellen des Steuerwinkels ∝ kann die Stromflussdauer ∝𝐶 während einer
Halbwelle der Speisespannung geändert werden und dadurch auch die vom Netz an den
Verbraucher gelieferte Leistung.
12
Am Ende einer jeden Halbwelle wird der Triac automatisch gelöscht, weil der Laststrom 𝑖𝐿 den
Haltestrom des Triacs 𝐼𝐻 unterschreitet. Der Triac wird zu Beginn einer jeden Halbwelle der
Speisespannung dann neu gezündet.
Das LC‐Entstörfilter begrenzt die Rückwirkungen des Wechselstromstellers (störende
hochfrequente Oberschwingungen des Laststromes) auf das speisende Stromnetz.
Durch Überbrückung des Dimmers mit dem Schalter S lässt sich der Fall ∝=0° eines idealen
Wechselstromstellers simulieren.
Durch den Spannungsteiler 𝑅1 , 𝑅2 , 𝑅3 wird die an der Glühlampe anliegende Spannung für
Messzwecke herabgesetzt. Aus Sicherheitsgründen wurde der Eingangswiderstand 𝑅1 + 𝑅3 =
300𝑘Ω des Spannungsteilers auf die beiden Eingangsleitungen gleichermaßen verteilt (siehe
Abbildung 2.9).
Für eine galvanische Trennung vom Netz ist unbedingt ein Trenntransformator einzusetzen.
Sonst besteht Lebensgefahr!
2.2.5 Magnetisierungsstrom eines Transformators im Leerlauf
Magnetische
Materialien
haben
nichtlineare
Magnetisierungskurven
mit
einer
Hystereseerscheinung (Abbildung 2.11 b). Aus diesem Grund ist der Magnetisierungsstrom
einer Induktivität bzw. eines Transformators mit einem magnetischen Kern unter Einspeisung
mit einer sinusförmigen Spannung nicht sinusförmig.
13
Abbildung 2.11: Graphische Bestimmung des Magnetisierungsstromes einer Induktivität. a) Speisespannung und
ihr Zeitintegral (magnetischer Fluss); b) Magnetisierungskurve; c) Magnetisierungsstrom); d) Schaltung
Induktionsgesetz: 𝛷 = − ∫ 𝑢(𝑡)𝑑𝑡
[2.14]
⃗ 𝑑𝐴 ≈ 𝐵 ∙ 𝐴 ⇒ 𝜙~𝐵
Magnetischer Fluss: 𝛷 = ∫𝐴 𝐵
[2.15]
⃗ 𝑑𝑙 = 𝐼𝑚 ∙ 𝑁 ⇒ 𝐼𝑚 ~𝐻
Durchflutungsgesetz: 𝜃 = ∮ 𝐻
[2.16]
Das Zeitintegral einer sinusförmigen Spannung ergibt einen ebenfalls sinusförmig verlaufenden
magnetischen Fluss Φ. Aufgrund der symmetrischen Form des Eisenkerns (siehe Abbildung 2.11
d) können die Vereinfachungen in Formel 2.15 und 2.16 getroffen werden. Jeder Momentanwert
des Flusses entspricht einem Wert der Induktion B. Abhängig von der Durchlaufrichtung der
Hystereseschleife, aufwärts bzw. abwärts, ergeben sich unterschiedliche Werte für die
entsprechende magnetische Feldstärke H bzw. für den Magnetisierungsstrom 𝐼𝑚 .
In Abbildung 2.11 ist die graphische Konstruktion des Magnetisierungsstromes dargestellt. Für
einige markante Werte des magnetischen Flusses (Nulldurchgänge und Scheitelwerte) kann man
den Zusammenhang zwischen Φ und 𝐼𝑚 (Punkte 1 bis 5) im Einzelnen verfolgen. Für andere Werte
des magnetischen Flusses erfolgt die Konstruktion ähnlicher Weise.
Diese Reihenfolge der graphischen Konstruktion entspricht nicht den physikalischen Abläufen.
Zusammengefasst lässt sich der physikalische Ablauf wie folgt erklären. Durch die angelegte
Spannung fließt ein Strom in dem Leiter. Der Strom erzeugt ein H‐Feld und somit über die
Permeabilität μ eine magnetische Flussdichte in dem Eisen. Der magnetische Fluss ergibt sich dann
über die Querschnittsfläche des Eisenkerns.
2.2.6 Spitzenwertgleichrichtung
Abbildung 2.12: Spitzenwertgleichrichtung a) Messschaltung; b) Zeitvariable Größen
14
Diese Schaltungen werden in der Impulstechnik und der Hochfrequenztechnik eingesetzt. Bei
den folgenden Schaltungen zur Messung von Spitzenwerten wird eine sinusförmige
Eingangsspannung angenommen.
Wenn an die Schaltung eine Spannung angelegt wird und der Kondensator noch entladen ist,
beginnt der Strom während der ersten positiven Halbwelle sofort durch die zunächst als ideal
betrachtete Diode zu fließen. Der größte Teil dieses Stromes lädt den Kondensator auf. Wenn
der Momentanwert des Signals kleiner wird als der erreichte Wert der Kondensatorspannung,
wird die Diode gesperrt. Danach entlädt sich der Kondensator durch das Messgerät bis zum
nächsten Zeitpunkt während der nächsten positiven Halbwelle, wo die Eingangsspannung den
Wert der Kondensatorspannung wieder überschreitet.
Die Diode wird jetzt wieder geöffnet, der Kondensator wird weiter aufgeladen bis die
Eingangsspannung wieder kleiner wird als die Kondensatorspannung. Nach einer gewissen Zeit,
die von den Auflade‐ bzw. Entladezeitkonstante abhängig ist, wird im Messkreis ein
eingeschwungener Zustand erreicht (stationärer Betrieb), bei dem die maximalen bzw. minimalen
Kondensatorspannungen zweier nacheinander folgender Perioden jeweils denselben Wert haben
(Abbildung 2.12). In diesem Versuch wird das System im eingeschwungenen betrachtet.
Wenn der Innenwiderstand der Spannungsquelle 𝑅𝑖 ≪ 𝑅𝑀 ist, gilt für die Aufladezeitkonstante
des Kondensators (Eingangsseite):
𝜏𝑎 ≈ 𝑅𝑖 𝐶
[2.17]
Und für die Entladezeitkonstante (Ausgangsseite):
𝜏𝑒 ≈ 𝑅𝑀 𝐶
[2.18]
Die Entladezeitkonstante muss ausreichend groß sein im Vergleich zu der Periodendauer 𝑇 der
Messspannung:
𝜏𝑒 = 𝑅𝑀 𝐶 = (10 … 100)𝑇
[2.19]
damit sich zwischen zwei aufeinanderfolgenden Aufladungen der Kondensator nur wenig
entlädt. Wiederum darf die Entladezeitkonstante nicht zu groß sein, damit die
Kondensatorspannung auch zeitlichen Änderungen der gemessenen Spitzenwerte folgen kann.
Merkmale:



Im stationären Zustand fließt der Strom nur während einer sehr kurzen Dauer, abhängig
von beiden Zeitkonstanten.
Die Schaltung ist nur anwendbar, wenn die Spannungsquelle für Gleichstrom durchlässig
ist.
Für die Kondensatorspannung ergibt sich mit einer reellen Diode und unter geringer
Entladung des Kondensators:
̂ − 𝑈𝐷 = √2𝑈 − 𝑈𝐷
𝑢𝑐 ≈ 𝑈
(𝑈𝐷 = Spannungsabfall an den Klemmen der Diode bei der Stromspitze)
15
[2.20]
2.2.7 Präzisions-Spitzenwertgleichrichtung
Abbildung 2.13: Präzisions‐Spitzenwertgleichrichtung mit Operationsverstärker
Hier arbeitet der Operationsverstärker als Spannungsfolger. Die Kondensatorspannung folgt
der Eingangsspannung jedoch nur beim Aufladevorgang, bis der positive Scheitelwert 𝑈𝑒
erreicht wird. Nachher wird die Diode gesperrt und der Kondensator beginnt sich langsam zu
entladen. Bei der nächsten positiven Halbwelle wird der Kondensator wieder auf den
Scheitelwert 𝑈𝑒 aufgeladen. Im Gegensatz zu der vorherigen Schaltung ohne Rückkoppelung
lädt sich hier der Kondensator auf den Spitzenwert der Eingangsspannung ohne Abzug der
Durchlassspannung der Diode. Im stationären Zustand, wenn die Entladezeitkonstante 𝜏𝑒 groß
genug ist, gilt:
̂𝑒
𝑢𝑎 = 𝑢𝑐 = 𝑈
[2.21]
Hier wird die Zeitkonstante 𝜏𝑒 ähnlich gewählt wie bei der klassischen Schaltung.
2.3 Versuchsausstattung
Die in dem vorherigen Kapitel erwähnten Schaltungen sollen in der Versuchsdurchführung
aufgebaut und untersucht werden. Alle für den Schaltungsaufbau benötigten Bauteile,
Messgeräte, Spannungsversorgungen und Kabel stehen an den Versuchsplätzen zur Verfügung.
16
2.3.1 Bauteile
Um den Schalungsaufbau zu vereinfachen und Berührungssicherheit zu gewährleisten sind alle
wesentlichen Baugruppen die in diesem Versuch vorkommen in Form von Modulboxen
vorgefertigt. Auf diesen Modulen findet man die jeweilige Darstellung der Schaltung und die
Anschlüsse für die Kabel zur weiteren Verschaltung. Als Beispiel ist das Modul der
Diodenbrücke in Abbildung 2.14 dargestellt.
Abbildung 2.14
Weitere Module im Versuch:
Wechselspannungsversorgung / Netztrafo
Eingang 230V, Ausgang 2 x 9V
Widerstandsmodul
2 x 1Ω, 1W
Widerstandsmodul
1kΩ, 1/3W
Spitzenwertgleichrichter
Siehe Kapitel 2
Präzisionsspitzenwertgleichrichter
Siehe Kapitel 2
Wechselstromsteller mit Glühlampe
Siehe Kapitel 2
Schaltung zur Messung des Magnetisierungsstromes
Siehe Kapitel 2
17
2.3.2 Trenn- und Regeltransformator
Die 230V Spannungsversorgung für die Versuchsaufbauten wird ausschließlich aus dem unten
abgebildeten Trenn‐ und Regeltransformator bezogen. Er stellt eine galvanische Trennung vom
Netz sicher. Die Ausgangsspannung kann über das Einstellrad in der Mitte Stufenlos zwischen
0 und 250V eingestellt und an der Anzeige abgelesen werden.
Abbildung 2.15: Trenn- und Regeltransforator
2.3.3 Oszilloskop
In dem Versuch wird ein digitales Speicheroszilloskop der Firma Tektronix der Serie
TDS2000B verwendet. Das Oszilloskop verfügt über vier Signaleingänge (Kanäle, Channels)
von denen im Rahmen dieses Versuchs drei benötigt werden. In diesem Versuch müssen auf
die Tastköpfe spezielle Adapter aufgesetzt werden um sie an die Anschlüsse der
Schaltungsmodule anschließen und Signale messen zu können. Aus diesem Grund wird die
Masse hier separat über den dritten Kanal angeschlossen. Über die Tasten CH1‐CH4 kann die
Anzeige des jeweiligen Kanals ein‐ und wieder ausgeschaltet werden. Die Drehknöpfe darüber
(POSITION) positionieren das Signal in vertikaler Richtung, besonders beim Vergleich zweier
Signale ist darauf zu achten, dass diese Verschiebung immer auf 0 eingestellt ist. Die
Drehknöpfe darunter (VOLT/DIV) dienen zur Einstellung der Skalenfaktoren. Der Knopf
POSITION im horizontalen Bedienfeld verschiebt das Signal auf der x‐Achse. SEC/DIV wählt
den horizontalen Skalenfaktor also die Zeitbasis. Um den Trigger manuell einzustellen betätigt
man den Knopf TRIG MENU. In dem Menu kann dann die Flanke, die Quelle, der Modus oder
eine Kopplung ausgewählt werden. Alternativ kann der Triggerpegel auch einfach über die
18
Taste „AUF 50% SETZEN“, auf den vertikalen Mittelpunkt zwischen den Spitzenwerten des
Signals, gesetzt werden. Die Einfachste Methode die Einstellungen vorzunehmen ist
Verwendung des AUTOSET Befehls. Betätigt man den entsprechenden Knopf stellt sich das
Oszilloskop so ein, das eine verwertbare Anzeige der Eingangssignale erzeugt wird. Aber wie
bei allen automatischen Einstellungen muss auch hier überprüft werden, ob geeignete
Einstellungen gewählt wurden. Um das Bild auf einem USB‐Datenträger zu speichern kann die
PRINT (Speichern) Funktion gewählt werden.
Abbildung 2.16 Oszilloskop
2.3.4 Multimeter
Das in diesem Versuch eingesetzte Multimeter ist ein TRMS-Multimeter. Im Rahmen dieses
Versuches werden nur die rechten Eingänge verwendet. Für Spannungsmessungen der rote und
der schwarze, für Strommessungen der schwarze und der weiße Eingang.
Abbildung 2.17: Multimeter
19
3 Verständnisfragen
Diese Fragen sind vor dem Versuchstermin zu bearbeiten
1. Wie ist der lineare Mittelwert einer periodischen Spannung definiert?
2. Welche Information liefert der lineare Mittelwert über eine Mischgröße?
3. Wie groß ist der lineare Mittelwert einer reinen Wechselspannung?
4. Welchen Wert zeigt ein Messgerät an wenn es Spannungen im Modus AC misst?
5. Welchen Wert zeigt ein Messgerät an wenn es Spannungen im Modus DC misst?
6. Wie ist der Gleichrichtwert definiert?
7. Wie wird der Gleichrichtwert auch bezeichnet?
8. Berechnen Sie den Gleichrichtwert einer sinusförmigen Spannung mit Amplitude 1V
9. Wie ist der Effektivwert einer periodischen Spannung definiert?
10. Wie kann der Effektivwert einer beliebigen nichtsinusförmigen Spannung ermittelt werden?
(Fourier)
11. Wie ist der Crest-Faktor definiert?
12. Wie ist der Formfaktor definiert?
13. Wie funktioniert die Brückenschaltung?
14. Wozu wird diese Schaltung verwendet?
15. Wie funktioniert die Grundschaltung zur Spitzenwertmessung?
16. Welchen Einfluss hat der Innenwiderstand des Messgerätes auf den zeitlichen Verlauf der
Kondensatorspannung bei dieser Schaltung?
17. Wie wird ein Operationsverstärker als Spannungsfolger/Impedanzwandler beschaltet?
18. Welche ist die wichtigste Eigenschaft dieser Schaltung?
19. Wo muss in dieser Schaltung eine Diode eingesetzt werden, damit ihre nichtlinearen
Verluste damit ausgeglichen werden?
20. Welche Rolle erfüllen die Elemente L und C in der Schaltung des Wechselstromstellers?
21. Warum ist der Magnetisierungsstrom einer Induktivität mit Eisenkern nicht sinusförmig?
22. Zeichnen Sie die Hysteresekurve der Magnetisierung.
23. Erklären kurz Sie anhand der Abbildung auf S. 14 wie der Verlauf des
Magnetisierungsstromes mit Hilfe der Speisespannung grafisch konstruiert werden kann.
20
4 Versuchsdurchführung
4.1 Grundeinstellungen
Multimeter:
Das Multimeter sollte zu Beginn des Versuches zurückgesetzt werden indem die
Tastenkombination Shift-Setup-Enter gedrückt wird.
Oszilloskop:
Die Schalter an den Messfühlern müssen auf 10 x stehen.
Folgende Einstellungen sollen am rechten Bildschirmrand zu sehen sein:
Kopplung: DC
Bandbreite: 20 MHz
Volts/Div: grob
Tastkopf: 10 x Spannung
Invertierung: Aus
Zusätzlich sollte im Trigger Menü die Trigger-Quelle auf Netz stehen
4.2 Brückengleichrichter mit ohmscher Last
Abbildung 4.1
a) Aufbau:
Bauen sie die Schaltung gemäß der Abbildung 4.1 auf und betreiben Sie sie mit 250V.
b) Oszillogramm:
Oszillographieren sie die Eingangsspannung 𝑢𝑒 sowie die Ausgangsspannung 𝑢𝑎 nacheinander.
Zeichnen sie beide Kurven in das Diagramm.
21
22
Um welche Art von Spannung handelt es sich bei 𝑢𝑎 ?
___________________________________________________________________________
Wie wird die Eingangsspannung im Gleichrichter verändert?
___________________________________________________________________________
Was bewirkt die Schaltung mathematisch?
__________________________________________________________________________
c) Messung:
Messen sie den Effektivwert des Wechselanteils der Eingangsspannung.
U e, w =__________
Messen sie den Mittelwert der Eingangsspannung.
𝑢̅𝑒 =__________
Lesen sie den Spitzenwert der Eingangsspannung am Oszilloskop ab.
𝑢̂𝑒 =__________
Berechnen sie daraus den Effektivwert der Eingangsspannung.
𝑈𝑒 =_______________=_______________=__________
Messen sie den Effektivwert des Wechselanteils der Ausgangsspannung.
𝑈𝑎,𝑤 =__________
Messen Sie den Mittelwert der Ausgangsspannung.
𝑢𝑎 =__________
Lesen sie den Spitzenwert der Ausgangsspannung am Oszilloskop ab.
𝑢̂𝑎 =__________
Berechnen sie daraus den Effektivwert der Ausgangsspannung.
𝑈𝑎 =_______________=_______________=__________
Welche Spannungsart liegt hier also an? (überprüfen sie ihre Vermutung aus b)
___________________________________________________________________________
23
d) Berechnungen:
Berechnen Sie den Gleichrichtwert der Eingangsspannung.
Hinweis: Gehen Sie von einer perfekten Sinusform aus.
Vergleichen Sie den berechneten Gleichrichtwert der Eingangsspannung mit dem gemessen
Ergebnis der Schaltung. Welchen Messwert müssen Sie dafür heranziehen und warum?
___________________________________________________________________________
___________________________________________________________________________
̅̅̅̅̅
|𝑢
𝑒 |=_________________
___=_________________________
__________________________________________________________________________
__________________________________________________________________________
Berechnen sie den theoretischen Formfaktor und den Crest-Faktor der Eingangsspannung.
𝐹𝑒,𝑡ℎ =_______________=_______________=__________
𝐶𝐹𝑒 =_______________=_______________=__________
Welche Aussage lässt sich mit dem Crest- und Formfaktor über die Eingangsspannung treffen?
___________________________________________________________________________
___________________________________________________________________________
Berechnen sie den Formfaktor und den Crest-Faktor der Ausgangsspannung. Welchem Wert
entspricht der Gleichrichtwert der Ausgangsspannung und warum?
̅̅̅̅̅
|𝑢𝑎 |=____
___________________________________________________________________________
𝐹𝑎 =______________________=________________________=__________
𝐶𝐹𝑎 =_____________________=________________________=__________
e) Parametervariation:
Drehen sie die Eingangsspannung so weit herunter, dass sich ein 𝑈𝑒 von 2V einstellt.
24
f) Oszillogramm:
Oszillografieren Sie erneut Eingangs- und Ausgangsspannung und zeichnen Sie beide in ein
gemeinsames Diagramm.
Was hat sich gegenüber der höheren Eingangsspannung verändert und warum?
___________________________________________________________________________
___________________________________________________________________________
g) Messungen:
Messen Sie alle nötigen Größen um die Effektivwerte der Eingangs- und Ausgangsspannung
sowie den Gleichrichtwert der Eingangsspannung zu berechnen.
___=__________
___=__________
___=__________
___=__________
___=__________
___=__________
___=__________
___=__________
𝑈𝑒 =_____________________=_____________________=__________
25
𝑈𝑎 =_____________________=_____________________=__________
̅̅̅̅̅
|𝑢
𝑒 | =____________________=_____________________=__________ (rein sinusförmig)
̅̅̅̅̅
|𝑢𝑎 | = ____
Berechnen sie nun erneut die Form- und Crest-Faktoren der Eingangs- und Ausgangsspannung.
𝐹𝑒 =_______________=_______________=__________
𝐶𝐹𝑒 =_______________=_______________=__________
𝐹𝑎 =_______________=_______________=__________
𝐶𝐹𝑎 =_______________=_______________=__________
26
4.3 Wechselstromsteller mit Phasenanschnittsteuerung und
ohmscher Last
Abbildung 4.2
a) Aufbau:
Bauen Sie die Schaltung gemäß Abbildung 4.2 auf und betreiben Sie sie mit 230 V.
b) Oszillogramm:
Oszillografieren Sie die Ausgangsspannung 𝑢𝑎 . Stellen sie dazu verschiedene Steuerwinkel
ein. Zeichnen Sie die Kurve bei einem Steuerwinkel von 90°.
27
Was bewirkt die Schaltung?
___________________________________________________________________________
Worauf sind die Schwingungen beim Einschalten des Triacs zurück zu führen?
___________________________________________________________________________
c) Messungen:
Messen sie für die Steuerwinkel 0°, 45°, 90°, und 135° alle nötigen Größen um die zugehörigen
Effektivwerte der Ausgangsspannung zu bestimmen.
Steuerwinkel:
0°
45°
90°
135°
𝑢𝑎
28
𝑈𝑎
d) Berechnungen:
Berechnen Sie für alle vier Steuerwinkel den Gleichrichtwert der Ausgangsspannung.
Hinweis: Lesen Sie den Scheitelwert des Sinus vom Oszilloskop bei 0° ab. Gehen Sie von
angeschnittenen perfekten Sinusspannungen aus. Einige Vorüberlegungen sind hier hilfreich.
𝑐𝑜𝑠(45°) =
√2
2
, 𝑐𝑜𝑠(135°) = −
√2
2
0°:
45°:
90°:
135°:
Steuerwinkel
0°
45°
90°
135°
̅̅̅̅̅
|𝑢𝑎 |
Berechnen sie u.a. mit den Größen aus c) die Formfaktoren sowie die Crest-Faktoren der
Ausgangsspannungen bei den unterschiedlichen Steuerwinkeln.
Steuerwinkel
0°
45°
90°
135°
𝑈𝑎
̅̅̅̅̅
|𝑢𝑎 |
𝑢̂𝑎
29
𝐹𝑎
𝐶𝐹𝑎
4.4 Transformator im Leerlauf
Abbildung 4.3
a) Aufbau:
Bauen Sie die Schaltung gemäß der Abbildung 4.3 auf und legen sie zunächst eine
Eingangsspannung 𝑈𝑒 von 230V an.
b) Oszillogramm:
Oszillografieren Sie die Transformatorspannung 𝑈𝑇𝑟 und den Magnetisierungsstrom bei
unterschiedlichen Werten für 𝑈𝑒 .und zeichnen Sie beide Oszillogramme für 𝑈𝑒 =230V in ein
Diagramm.
30
Wie kommt die Verzerrung des Magnetisierungsstromes zu Stande?
___________________________________________________________________________
c) Messungen
Messen sie für alle in der Tabelle angegebenen Eingangsspannungen den Effektivwert der
Spannung am Transformator 𝑈𝑇𝑟 sowie den Effektivwert des Magnetisierungsstroms𝐼𝑚 .
Eingangsspannung 𝑈𝑒 :
50V
100V
150V
200V
250V
𝑈𝑇𝑟
𝑖𝑚
𝐼𝑚
4.5 Einfacher Spitzenwertgleichrichter
Abbildung 4.4
a) Aufbau:
Bauen sie die Schaltung gemäß der Abbildung 4.4 auf und belasten sie die Schaltung mit 𝑅𝑀 =
20𝑘Ω. Betreiben sie die Schaltung zunächst mit 𝑈𝑒 =10V.
b) Verständnis:
Erklären sie kurz in eigenen Worten wie die Schaltung funktioniert und was bei 𝑢𝑎 gemessen
werden kann.
___________________________________________________________________________
___________________________________________________________________________
c) Berechnungen
Berechnen sie die Auflade- und Entladekonstante des Kondensators C. (Hinweis: [Ω]∙[F]=[s])
𝜏𝑎 = 𝑅𝑖 ∙ 𝐶 =_________________________=__________
31
𝜏𝑒 = (𝑅𝑀 ||𝑅′𝑀 ) ∙ 𝐶 ≈ 𝑅𝑀 ∙ 𝐶 =_________________________=__________
Wie lange dauert es (in Periodendauern) den Kondensator zu laden bzw. zu entladen?
Aufladung:__________
Entladung:__________
d) Oszillogramm:
Oszillografieren Sie gemeinsam die Eingangs- und Ausgangsspannung der Schaltung.
Zeichnen Sie die Kurven in ein gemeinsames Diagramm.
Oszillografieren Sie danach qualitativ den Verlauf des Diodenstromes, indem sie die Spannung
über dem Widerstand 𝑅𝑖 abgreifen. Zeichnen sie diesen ebenfalls in das Diagramm.
Welche Spannung lässt sich am Ausgang der Schaltung 𝑢𝑎 messen?
___________________________________________________________________________
e) Parametervariation:
Schalten Sie nun den Schalter S aus, sodass nur noch der Innenwiderstand 𝑅′𝑀 des Oszilloskops
die Schaltung belastet.
32
f) Berechnung:
Berechnen sie erneut die Entladedauer des Kondensators C wenn er sich einzig über den
Innenwiderstand des Oszilloskops entlädt.
𝑇𝑒 =_________________________=__________
Wie wird sich die veränderte Entladedauer im Oszillogramm bemerkbar machen?
___________________________________________________________________________
g) Oszillogramm:
Zeichnen Sie das Oszillogramm der Eingangs- und Ausgangsspannung 𝑢𝑒 und 𝑢𝑎 sowie den
Diodenstrom in ein gemeinsames Diagramm.
Überprüfen Sie ihre These aus f).
___________________________________________________________________________
Wird bei der veränderten Schaltung an 𝑢𝑎 der echte Spitzenwert gemessen?
___________________________________________________________________________
h) Parametervariation:
33
Drehen Sie die Eingangsspannung soweit herunter bis sich ein 𝑈𝑒 von 1V einstellt. (Der
Schalter S bleibt aus)
i) Oszillogramm:
Zeichnen Sie erneut das Oszillogramm der Eingangs- und Ausgangsspannung 𝑢𝑒 und 𝑢𝑎 in ein
gemeinsames Diagramm.
überprüfen Sie Ihre These aus g).
___________________________________________________________________________
Woher stammt die Abweichung zum Oszillogramm aus g)?
___________________________________________________________________________
34
4.6 Präzisions-Spitzenwertgleichrichter
mit
Operationsverstärker
Abbildung 4.5
a) Aufbau:
Bauen Sie die Messschaltung gemäß der Abbildung 4.5 auf. Betreiben sie die Schaltung mit
𝑈𝑒 =1V.
b) Oszillogramm:
Oszillografieren sie die Größen 𝑢𝑒 und 𝑢𝑎 und zeichnen Sie beide in ein gemeinsames
Diagramm.
35
Vergleichen sie das Diagramm mit dem aus Aufgabe 4.5 i). Erklären Sie die Abweichung
___________________________________________________________________________
c) Messungen:
Messen Sie den Spitzenwert der Eingangsspannung 𝑢̂𝑒 mit dem Multimeter.
𝑢̂𝑒 =__________
36
5 Anmerkung zur Ausarbeitung (Wirt-Ings.)
Bitte als .pdf senden an: [email protected]
Die Ausarbeitung soll wissenschaftlich korrekt verfasst werden. Das Bedeutet u.a.:



Ausnahmslos Präsens, Konjunktiv
Kein „ich“ „wir“ „er“ „man“
Keine Umgangssprache
Unwissenschaftliche Ausarbeitungen werden nicht benotet!
Umfang: 5 DIN A4 Seiten mit Schriftgröße 12. (ohne Deckblatt, Inhaltsverzeichnis und
Anhang)
1. Deckblatt mit:
 Versuchsbezeichnung (Nummer und Titel)
 Fakultät
 Datum und Uhrzeit der Versuchsdurchführung
 Abgabetermin der Ausarbeitung
 Name, Vorname, Matrikelnummer, Studiengang und Fachsemester jedes Teilnehmers,
jeder Teilnehmerin
2. Gliederung der Auswertung (Inhaltsverzeichnis)
3. Einleitende Beschreibung der Zielsetzung und Abgrenzung der Aufgabenstellung mit:
 Sachanalyse (Ziel des Versuches, globale Aufgabenstellung)
 Elementaranalyse (Grobsegmentierung, Teilziele)
 Operationalisierung (Systematik der Bearbeitung, Vorgehensweise)
4. Detaillierte Beschreibung des Experimentes mit:
 Apparativer Ausstattung
 Schaltbild
 Ggf. Sicherheitshinweisen
5. Dokumentation
der
Versuchsdurchführung
und
der
Ergebnisse
(inkl.
Vorbereitungsaufgaben)
 Aufgaben- resp. Teilaufgabenstellung
 Aufgabenspezifische Beschreibung des Aufbaus, der Vorgaben und der Einstellungen
(Parameter, Sollwerte)
 Wertfreie Wiedergabe der Beobachtungen und Ergebnisse
 Interpretation und Einordnung der Ergebnisse im Hinblick auf die Aufgabenstellung,
ggf. Fehlerbetrachtung
6. Zusammenfassung (Fazit)
7. Anhang mit:
 Sauber ausgefülltem Versuchsdurchführungsteil dieser Versuchsanleitung
37