Masse D Definition “Masse” 1. Jeder Körper wird von der Erde
Werbung

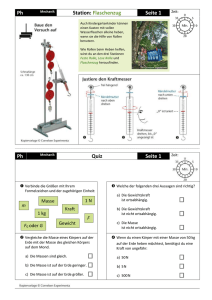
! Masse D! Definition “Masse” ! ! ! ! ! ! ! ! ! ! ! M! ! 1. Jeder Körper wird von der Erde angezogen. ->!Jeder Körper besitzt eine so genannte schwere Masse, welche die Ursache für ! diese Anziehung abgenommen wird. 2. Jede Masse hat die Eigenschaft ihren Bewegungszustand beibehalten zu wollen. ->!Eine Änderung des Bewegungszustandes eines Körpers erfolgt nie ohne ! Ursache. ->!Die Ursache diesen trägen Verhaltens eines Körpers ist eine träge Masse. -> träge Masse (mt) ≡ schwere Masse (ms) ? ! (Diese Frage ist ein Teilgebiet der aktuellen Forschung, nicht eindeutig geklärt) -> In der Schule ist mt = ms = m ! [m] = kg! m : Masse ->!Die Ursache der Änderung des Bewegungszustandes eines Körpers ist immer ! eine Kraft ! Kräfte D! Definition “Kraft” ! ! ! Eine Kraft ist die Ursache für eine Bewegungsänderung oder eine Formveränderung F∼m F∼m⋅a F=m⋅a F∼a B! ! ! ! Bemerkung Ist eine Größe A direktproportional zu einer Größe B und auch direktproportional zu einer Größe C so gilt, dass A auch direktproportional zu B ⋅ C ist. [F] = [m] ⋅ [a] ! ! = kg ⋅ ! ! = N (Newton) ! Die Newtonschen Axiome / Prinzipien D! Definition Trägheitsgesetz / Trägheitsprinzip ! ! ! Wird auf einem Körper keine Kraft, so verbleibt er im Zustand der Ruhe oder der geradlinigen gleichförmigen Bewegung = 0 V ≡ Konstant D! Definition Wechselwirkungsgesetz / Wechselwirkungsprinzip ! ! Wenn eine Kraft ! auf einem Körper wirkt, die ihren Ursprung in einem andern Körper hat, so wirkt auf diesen eine entgegengesetzte gleich große Kraft -! . ≡ - ! D! Definition Kraftgesetz / Aktionprinzip ! ! Wenn eine Kraft ! auf einen Körper mit der Masse m wirkt, so beschleunigt sie diesen mit ! . =m⋅a ! Bsp! Beispiel ! ! ! ! Welche Kraft muss man aufbringen, um ein Auto m = 2,5t mit a) 7! zu beschleunigen. Geg.: m = 2,5t! a = 7 Ges.: F ! ! ! Geg.: m = 2,5t! a = 7,0 Ges.: F und b) 7,0 ! ! ! ! ! ! Ein Fahrstuhl m = 300kg soll vom EG in den 1.Stock fahren. Im Fahrstuhl befinden sich: Flittner: 93 kg; Knobl: 75kg; Eichner: 80kg; Kainz: 58kg; Rieß:74kg; Gottsmann: 87kg; Mahnke: 81kg. An den Fahrstuhl zieht eine Kraft von 15kN. Welche Beschleunigung erfährt der Fahrstuhl? ! ! Geg.: m = 848kg! Ges.: aR ! ! ! ! ! FZ = 15kN! g = 9,81 ! Gewichtskraft D! ! ! Gewichtskraft Jede Masse wird in Erdnähe mit g = 9,81! [und zwar in Richtung des Erdbodens] ! ! ! ! -> FG = 9,81 -> FG = g ⋅ m -> Für jeden Himmelskörper existiert eine individuelle Gravitationsbeschleunigung ! bzw ein individueller Ortsfaktor. ! gMond = 1,62! ! ! ! ! Bezeichnung g! - Ortsfaktor ! - Fallbeschleunigung ! - Gravitationsbeschleunigung beschleunigt gJupiter = 24 Bsp! Beispiel ! ! ! B! ! In der Umgangssprache meint man mit der Angabe von “12 kg” oft nicht die Masse, sondern die Gewichtskraft ! ! Das Kräfteparallelogramm [Vektor Addition von Kräften] ! Das Kräftegleichgewicht ! FG = 5kg ⋅ 9,81! = 49,05N ≈ 5 ⋅10¹N ! ! ! ->!Da sich die aufgehängte Masse nicht bewegt, muss die Summe alle Kräfte gleich ! Null sein. ->!Die Decke zieht mit der Kraft! an der aufgehängten Masse. D! Definition Kräftegleichgewicht ! ! Erzeugen zwei oder mehrere Kräfte bei einem Körper keine Änderung des Bewegungszustandes so spricht man vom Kräftegleichgewicht. Bsp! Beispiel Kräftezerlegung ! ! ! ! Oft ist von allen an einem Körper angreifenden Kräften nur die resultierende Kraft erkennbar. -> Ziel ist es, die unbekannten Teilkräfte zu bestimmen -> Kräfteparallelogramm (Methode) Bsp! Beispiel 1.! einzeichnen (bzw die Resultierende Kraft) 2. Verlängern durch Fußpunkt von 3. Einzeichnender Parallelen zu den Kraftlinien ! durch die Spitze von 4. Aufstellen des Kräfteparallelogramm 5. Man erhält die Beträge von ! über die Geometrie des ! Parallelogramms mit α, β, B! Bemerkung Pythagoras: a² + b² = c² ! Hohensatz: h² = p ⋅ q Sinussatz: Cosinussatz: c² = a² + b² - 2 ⋅ a ⋅ b ⋅ cos(γ) a² = b² + c² - 2 ⋅ b ⋅ c ⋅ cos(α) b² = a² + c² - 2 ⋅ a ⋅ c ⋅ cos(β) Tragekonstruktionen D! ! ! ! Definition Tragekonstruktion ●! Tragekonstruktionen bestehen aus Seilen und/oder “Stäben” ●! Bei Tragekonstruktionen müssen Seile und “Stäben” so bemessen werden, dass ! sie den Belastungen stand halten. B! Bemerkung ! ! 1. Seile sind nur in Zugrichtung belastbar 2. Ein Stab kann auf Zug-, Schub- oder Querkräften belastet werden. M! Merke ! ! Die durch Kraft! in einem Punkt einer Tragekonstruktion hervorgerufenen Zug- bzw. Schubkräfte findet man mittels Kräftezerlegung. Bsp! Beispiel ! F1 = F2 = FG, da das Dreieck gleichschenklig ist. -> F1² + F2² = FG² -> F2 = FG ⋅ ! Kräfte an der Schiefen Ebene ! ! ! ! FH = Dieser Kraftteil treibt den Würfel den Hang hinab Hangabtriebskraft FN = Dieser Kraftanteil drückt den Würfel auf die Ebene Normalkraft ! Die Neigung der Ebene (α) erzeugt prinzipiell die zwei Kraftanteile B! Bemerkung ! Kräftedreieck ! FH = FG ⋅ sin(α) ! FN = FG ⋅ cos(α) ! Reibungskräfte Zum ersten Anschieben und zum Bewegen eines Körpers auf einer Oberfläche (Bewegen mit v ≡ Konstant) ist eine Kraftwirkung (FZ) erforderlich -> Es muss eine Kraft FR geben die FZ entgegen wirkt ! Woher Kommt diese Kraft? Oberfläche und Klotz sind mikroskopisch verzahnt. -> Schiebt man den Klotz an, so widersteht er einer Maximalkraft FH bevor er seinen Bewegungszustand ändert. FH : Die Haftreibungskraft ! ! ! Ist der Klotz bereits in Bewegung, ist eine Minimalzustand notwendig um den Bewegungszustand des Klotzes zu erhalten. Die Kraft, die diese Minimalkraft notwendig macht ist FR : Die Reibungskraft/Gleitreibungskraft ! Im Allgemeinen gilt : FH > FR ! Wir nehmen an: ! ! 1. FH; FR seien geschwindigkeitsabhängig 2. Es gilt nährungsweise FZ1 = FZ2 FH & FR sind unabhängig von der Kontaktfläche ! ! ! ! ! ! ! ! ! ! 0 < µR < µH <1 ! FH = µH ⋅ FG FR = µR ⋅ FG ! ! ! ! ! µH = Haftreibungskoeffizient ! ! (Haftzahl) ! µR = Gleitreibungskoeffizient ! ! (Gleitzahl) B! ! ! Bemerkung Die Haftreibungszahlen müssen individuell für jedes Kontaktflächenpaar bestimmt werden. Bsp! Beispiel M! ! Werkstoff µH µR Stahl auf Stahl 0,2 0,06 Holz auf Holz 0,6 0,4 Metall auf Holz 0,6 0,3 Reifen auf Asphalt 0,8 0,6 Reifen auf Eis 0,1 0,05 Merke! Reibung auf der Schiefen Ebene hängt nur von der Normalkraft FN ab. FH = µH ⋅ FN FR = µR ⋅ FN ! Hebel D! Definition ! ! Ein Hebel ist ein Starrer Körper, der um einen fixen Arbeitspunkt drehbar ist. -> Ein Heben ist ein Kraftwandler ! Hebeltypen ! 1. Zweiseitiger Hebel z.B. Wippe ! 2. Einseitiger Hebel z.B. Nussknacker D! Definition Drehmoment ! ! ! M = F⋅ r gilt nur wenn F ⊥ r [M] = [F] ⋅ [r]! = N ⋅m ! = J (Joule) M! Gleichgewicht an einem zweiseitigen Hebel ! ! Befinden sich ein zweiseitiger Hebel im Gleichgewicht so sind das linksseitige und das rechtsseitige Drehmoment gleich. Bsp! Beispiel Ml = M r FG1 r1 = FG2 ⋅r2 mM ⋅ g ⋅ r1 = mM ⋅g ⋅ r2 mM ⋅ r 1 = m E ⋅ r 2 ! ! mM = 100g! mE = 3t! r2 = 1m Ml = Mr ≡ mM ⋅r1 = mE ⋅r2 ! ! ! ! M! Gleichgewicht an einem einseitigen Hebel ! ! ! Wegen der entgegengesetzten Drehrichtung gilt auch beim einseitigen Hebel, dass er sich im Gleichgewicht befindet, solange das linksgerichtete und das rechtsgerichtete Drehmoment gleich sind. Ml = M r F1 ⋅ r1 = F2 ⋅r2 ! Kraftwandler ! Kraft als Vektor D! Definition Kraftwandler ! ! Ein Kraftwandler ist eine mechanische Vorrichtung, die den Angriffspunkt und / oder den Betrag und / oder die Richtung einer Kraft ändern kann. Bsp! Beispiel ! 1. Änderung des Angriffspunkts ! ! 2. Änderung der Richtung ! ! 3. Änderung des Betrags F = F2 ⋅cos(α) ! !! ! Flaschenzug B! ! ! Bemerkung Ein Flaschenzug ist ein Kraftwandler, der aus Rollen, Seilen und Aufhängungen besteht. ! Bestandteile ! 1.) Feste Rolle / Umlenkrolle! 2.) Lose Rolle Bsp! Beispiel D! Definition Flaschenzug ! ! Ein Kraftwandler der aus einem System von festen und losen Rollen besteht, wird Flaschenzug genannt. ! Flaschenzugtypen ! 1.) “Normaler Flaschenzug”! D! Die goldene Regel der Mechanik ! ! Erzeugt ein Kraftwandler eine -fache Kraftuntersetzung, so erzeugt er gleichzeitig eine n-fache Wegübersetzung. 2.) “Potenzflaschenzug” Bsp! Beispiel FG || ∆S1 und F2 || ∆S2