Grundzüge von Datenstrukturen und Algorithmen (WS 2013/2014

Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Aufgabe 1
Die DFS-Aufrufe ergeben sich wie folgt:
DFS(1), DFS(3), DFS(2), DFS(6), DFS(7), DFS(4), DFS(8), DFS(9), DFS(5)
Nach Ausführung von DFS(1) ergeben sich:
d = [1, 3, 2, 6, 10, 4, 5, 7, 9]
f = [18, 16, 17, 13, 11, 15, 14, 8, 12]
predecessor = [N U LL, 3, 1, 7, 9, 2, 6, 4, 4]
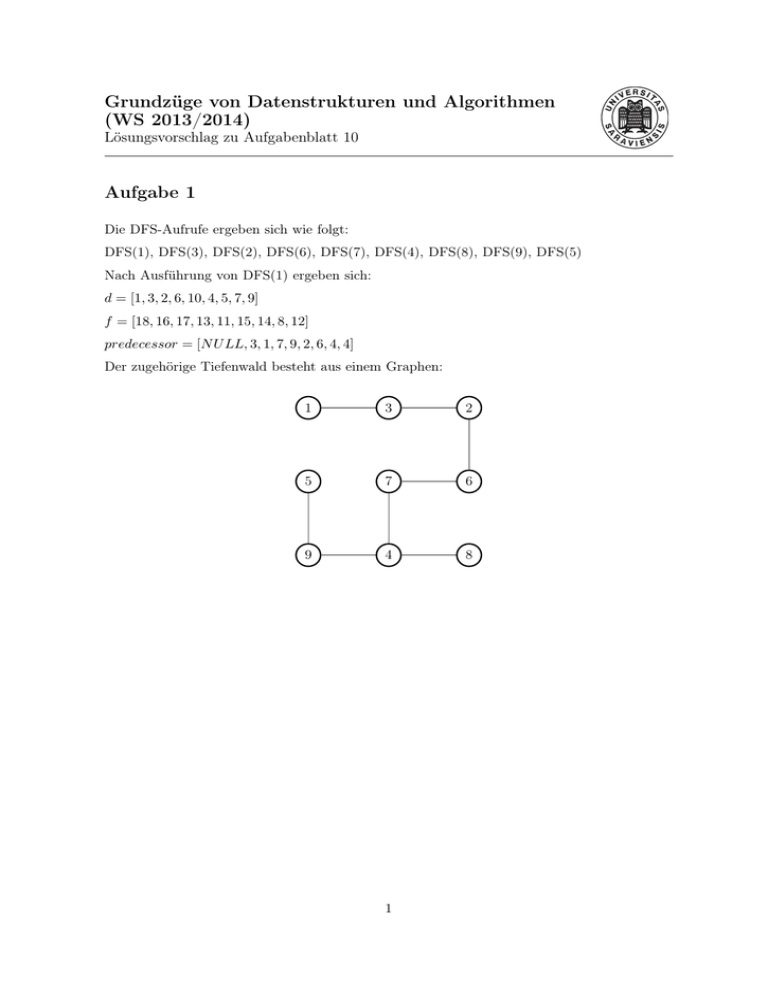
Der zugehörige Tiefenwald besteht aus einem Graphen:
1
3
2
5
7
6
9
4
8
1
Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Aufgabe 2
Anhand des Graphen G = (V, E) konstruieren wir den Graphen Ga = (V, Ea ) für reelle a wie
folgt: Ea = {e ∈ E|k(e) ≥ a}
Nun lässt sich der Durchfluss von s nach t definieren als das maximale a, so dass im Graphen
Ga = (V, Ea ) ein Pfad von s nach t existiert.
Wir wenden binäre Suche zwischen min{k(e)|e ∈ E} und max{k(e)|e ∈ E} an, um dieses
optimale a zu finden. Da jeder Kante genau ein Gewicht zugeordnet wird, führen wir binäre
Suche über m = |E| Elemente aus. Dies hat eine Laufzeit von m.
Um für ein gegebenes a zu ermitteln, ob Ea einen Pfad von s nach t enthält, rufen wir
DFS(Ga ,s) auf. Die Laufzeit der Tiefensuche beträgt n + m, wobei n die Anzahl der Knoten
n = |V | darstellt.
Existiert ein solcher Pfad für einen Wert m, so muss im Bereich a ≥ m weitergesucht werden.
Existiert kein Pfad von s nach t, so war m zu optimistisch und es muss im Bereich a < m
gesucht werden.
Korrektheit: Sei die Menge aller möglichen Pfade in G von s nach t gegeben als P . Jedem Pfad
p aus P ist eine Kapazität k(p) zugewiesen. Der Durchfluss ist definiert als d = max{k(p)|p ∈
P }. Es existiert also ein Pfad pmax = (e1 , ..., el ), so dass min{k(ei )|1 ≤ i ≤ l} = d. Dies bedeutet, dass alle Kanten in diesem Pfad eine größere Kapazität als d besitzen. Somit existieren
diese auch in Ed . Alle anderen Pfade aus P enthalten mindestens eine Kante, deren Kapazität
kleiner als d ist. Somit existieren diese Kanten in Ed nicht mehr. Tiefensuche auf Gd findet
für d einen Pfad, für größere Werte ist dies nicht mehr möglich, somit terminiert binäre Suche
und der gesuchte Durchfluss ist d.
Laufzeit: In jeder Iteration von BS wird einmal DFS aufgerufen, somit ergibt sich insgesamt
eine Laufzeit von (n + m) log m.
2
Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Aufgabe 3
u.d
3
Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Starke Zusammenhangskomponenten
4
Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Aufgabe 4
Idee
Wir bilden einen Graphen G0 = (V, E 0 ) aus G = (V, E), in dem die Kanten jeweils die
entgegengesetzte Richtung haben, das heißt:
(u, v) ∈ E ⇐⇒ (v, u) ∈ E 0
Auf diesem Graphen wenden wir ausgehend von jedem Krankenhaus-Knoten r eine Tiefensuche an und tragen für jeden Knoten, auf den wir gelangen, r als erreichbaren KrankenhausKnoten ein.
Die Graphen stellen wir mithilfe von Adjazenzlisten dar.
Algorithmus
berechne_erreichbare_krankenhaus_knoten
f\"ur i <- 1 bis |V| tue
f\"ur alle Kanten (i, j) in G
f\"uge der Adjazenzliste von j in G’ den Knoten i hinzu
f\"ur i <- 1 bis |V| tue
besucht[i] <- falsch
r[i] <- BOTTOM
f\"ur alle Krankenhaus-Knoten r aus R
tue wenn nicht besucht[r] dann dfs(r, r)
dfs(Knoten u, Marke r)
r[u] <- r
besucht[u] = wahr
f\"ur alle Kanten (u, v) aus E’ tue
wenn nicht besucht[v] dann dfs(v, r)
Korrektheit
Es gilt, dass wenn v von u aus in G erreichbar ist, auch u von v in G0 erreicht werden kann
(durch Ümdrehenäller Kanten auf dem Pfad). Wenn wir also eine Tiefensuche von einem
Krankenhaus-Knoten r in G0 machen, so werden wir alle Knoten besuchen, von denen dieser
Krankenhaus-Knoten r in G erreicht werden kann. Wir markieren diese mit r und müssen
sie in den weiteren Tiefensuchen nicht mehr betrachten, da sie bereits einem erreichbaren
Krankenhaus-Knoten zugeordnet werden konnten und auch alle Nachfahren im Tiefensuchbaum diesem Knoten zugeordnet werden können.
5
Grundzüge von Datenstrukturen und Algorithmen
(WS 2013/2014)
Lösungsvorschlag zu Aufgabenblatt 10
Da die Einträge für alle Knoten mit ⊥ initialisiert wurden, wird jedem Knoten, der in keiner
der Tiefensuchen erreicht wird, von ihnen also keine Krankenhaus-Knoten erreichbar ist, der
Wert ⊥ zugeordnet, jeder andere Knoten wird mit einem von ihm erreichbaren KrankenhausKnoten markiert.
Laufzeit
Zunächst müssen wir G0 aus G generieren, was in einer Zeit von O(|V | + |E|) möglich ist,
da die Schleife über alle Knoten iteriert und in der Doppelschleife jede Kante genau einmal
betrachtet wird.
Die folgende Initialisierung durchläuft jeden Knoten einmal, benötigt also O(|V |). Danach
werden die Tiefensuchen ausgeführt, wobei der Test, ob der Knoten bereits besucht wurde,
verhindert, dass für einen Knoten mehr als einmal dfs() ausgeführt wird.
Da es maximal ein dfs()-Aufruf für jeden Knoten geben kann, wird jede Kante in der Schleife in
dfs() höchstens einmal berührt, da sie nur von einem Knoten ausgeht und somit nur in dessen
dfs()-Aufruf betrachtet werden kann. Folglich wird jede Kante und jeder Knoten maximal
einmal im Verlauf des Alorithmus’ verarbeitet.
Die resultierende Gesamtzeit liegt in O(|V | + |E|).
6