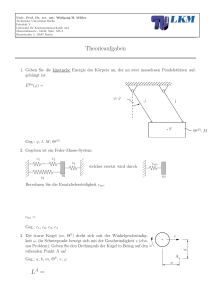
Aufgabe 1 er ez P A B D ψ r1 r2 ω1 ω3 1. Geschwindigkeit vB des

Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 1
SS 2012
Aufgabe 1
B
r2
ψ
r1
P
er
A
ω3
ez
D
eϕ
ω1
1. Geschwindigkeit vB des Planetenradmittelpunktes:
3
v B = ω 3 × rAB = ω3 ez × (r1 + r2 )er
= ω3 (r1 + r2 )eϕ
3
2
vB = vB
Gelenk!
(1)
(2)
2. Winkelgeschwindigkeit des Planetenrades ω2 :
1
v D = ω1 × r AD
2
2
v D = v B + ω2 × r BD
1
2
Bei reinem Rollen ist v D = v D :
2
ω1 × r AD = v B + ω 2 × r BD
= ω3 × r AB + ω 2 × rBD
ω1 ez × r1 er = ω3 ez × (r1 + r2 )er + ω2 ez × (−r2 )er
ω1 r1 eϕ = ω3 (r1 + r2 )eϕ − ω2 r2 eϕ
r1
ω3 − ω1
ω2 = ω3 +
r2
3. Geschwindigkeitsvektor des Punktes P:
2
2
v P = v B + ω2 × r BP
= ω3 (r1 + r2 )eϕ + ω2 ez × a cos ψer + sin ψeϕ
h
h
i
i
= −a sin ψ ω3 + r1 /r2 (ω3 − ω1 ) er + ω3 (r1 + r2 ) + a cos ψ ω3 + r1 /r2 (ω3 − ω1 ) eϕ
(3)
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 2
SS 2012
Aufgabe 2
Es soll das Massenträgheitsmoment von einem Zylinder mit Masse M , Radius R, Länge L und Dichte ρ berechnet
werden. Das Trägheitsmoment bezogen auf die (Dreh-)z-Achse für rotationssymmetrische Körper ist gegeben durch:
Θzz =
Z
r2 dm
,
M
wobei r den radialen Abstand von der z-Achse meint. Wir wählen Zylinderkoordinaten. Es gilt nun, einen Ausdruck
für das infinitesimale Massenelement dm zu finden.
z
r
ϕ
Zunächst gilt:
dm = ρ dV
und für das Differentialvolumenelement lässt sich in Zylinderkoordinaten schreiben:
dV = dr · r dϕ · dz
Damit ergibt sich:
Θzz = ρ
Z
L
2
−L
2
Z
0
2π
Z
R
R4
1
2πL = ρLπR4
4
2
r3 dr dϕ dz = ρ
0
.
Mit der Gesamtmasse M = ρV = ρLπR2 folgt:
Θzz =
1
M R2
2
.
Alternativ könnte man auch gleich die Integration über einzelne Hohlzylinder vornehmen und für dV schreiben:
dV = L · 2πr dr
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 3
SS 2012
Aufgabe 3
(a)
1 ist ein Punkt auf dem Rand des Sonnenrads. Er hat dieselbe Geschwindigkeit
wie ein Punkt des Planetenrads, der zum betrachteten Zeitpunkt an derselben
Stelle ist (reines Rollen).
Die Eulersche Geschwindigkeitsformel liefert:
1
a1
v 1 = 0 + ω 1 × a1 er
= ω1 ez × a1 er
er
= a1 ω 1 e ϕ
ω1
eϕ
ez
2
2 ist ein Punkt auf dem Innenrand des Hohlrads. Er hat dieselbe Geschwindigkeit wie ein
Punkt des Planetenrads, der zum betrachteten Zeitpunkt an derselben Stelle ist (reines Rollen).
Es folgt wie oben:
er
a2
v 2 = 0 + ω 2 × a2 er
= a2 ω 2 e ϕ
ω2
v2
Kennt man die Geschwindigkeiten zweier Punkte eines Starrkörpers, so können die
Geschwindigkeiten der Punkte auf der Geraden zwischen den 2 Punkten durch lineare
Interpolation berechnet werden. Die Geschwindigkeitsverteilung ist linear. Speziell gilt
hier:
vx
a2 − a1
v1
vx = v1 +
x
(v − v 1 )
a2 − a1 2
(4)
x
Der Mittelpunkt des Planetenrades bewegt sich also mit der Geschwindigkeit:
1
1
v = v 1 + (v 2 − v 1 ) = (v 1 + v 2 )
2
2
1
|v| = v = |v 1 + v 2 |
2
1p
(a1 ω1 + a2 ω2 )2
v=
2
1
= (a1 ω1 + a2 ω2 )
2
Die Geschwindigkeit im Mittelpunkt des Rads ist also der Mittelwert aus oberster und unterster Geschwindigkeit.
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 4
SS 2012
(b) Eulersche Formel auf dem Planetenrad:
v 2 = v 1 + ω × (a2 − a1 )er
(a2 ω2 − a1 ω1 )eϕ = ωez × (a2 − a1 )er
a2 ω 2 − a1 ω 1
ω=
a2 − a1
(c) Die Geschwindigkeit des Planetenradträgers ist an einem Punkt bekannt, sie muss nämlich mit der des Planetenradmittelpunkts übereinstimmen. Daher gilt:
veϕ = ω ∗ ×
a1 + a2
er
2
2v
a1 + a2
a1 ω 1 + a2 ω 2
=
a1 + a2
ω∗ =
Aufgabe 4
(a) Freischnitt der einzelnen Körper:
F
II
a
FAz
R
I
ϕ
FR
r
FN
FAx
FR
b
G1
G2
FBx
S
FBz
III
z
mg
Nun werden der Schwerpunktsatz und der Drallsatz für jeden Freischnitt aufgestellt.
Körper I:
Der Hebel befindet sich im statischen Gleichgewicht. Aus dem Schwerpunktsatz erhält man:
X
Fx = F − FN + FBx
ex : maIx = 0 =
X
ez : maIz = 0 =
Fz = −FBz + G1 − FR
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 5
SS 2012
Diese beiden Gleichungen ermöglichen die Bestimmung der unbekannten Lagerreaktionen FBx und FBz , die hier
jedoch nicht interessieren.
Der Drallsatz liefert:
X
a
Θϕ̈ = 0 =
M B = −F (a + b) + FN b = 0 ⇒ FN = F ( + 1)
(5)
b
Mit dem Coulombschen Reibgesetz ergibt sich:
a
FR = µFN = µ( + 1)F
b
(6)
Körper III:
Der Drallsatz und der Schwerpunktsatz in ex -Richtung am Körper III liefern nur die wahre aber triviale Aussage
0 = 0. Nur der Schwerpunktsatz in ez -Richtung ist interessant:
ez : mz̈ = mg − S
⇒ S = m(g − z̈)
(7)
(8)
Körper II:
Der Schwerpunktsatz liefert die zwei Bestimmungsgleichungen für die Lagerreaktionen FAz und FAx :
X
ex : maIIx = 0 =
Fx = FN + FAx
X
ez : maIIz = 0 =
Fz = −FAz + G2 + S + FR
Drallsatz:
Der Drehsinn ist linksherum positiv, man beachte die Wahl der Zählrichtung von ϕ (s. Freischnitt):
X
−ΘA ϕ̈ =
MA
A
⇒ −Θ ϕ̈ = RFR − Sr
(9)
(10)
Gleichungssystem umformen und Kinematik:
Einsetzen von (6) und (8) in (10):
a
⇒ ΘA ϕ̈ = −RµF ( + 1) + mr(g − z̈)
b
(11)
Diese Gleichung enthält noch zu viele Unbekannte. Eine weitere Gleichung erhalten wir aus der Kinematik. Das
System hat nur einen Freiheitsgrad. Ist Bewegung der Scheibe bekannt, so ist auch eindeutig, wie sich die Masse
bewegt. Es gilt nun den Zusammenhang zwischen den Koordinaten ϕ und z aus der Kinematik zu finden:
rϕ̇ = ż ⇒ ϕ̇ =
ż
r
(12)
Einsetzen dieses Zusammenhangs in (11) liefert nach Umstellen:
⇒(
ΘA
a
+ mr)z̈ = mgr − µRF ( + 1)
r
b
mgr − µ( ab + 1)RF
⇒ z̈ =
ΘA
r + mr
(13)
(14)
Nun ist die Gleichung reduziert auf die Unbekannte z̈ und das gesuchte F . Die letzte nötige Gleichung erhalten wir
aus der Bedingung, dass das System zur Zeit T zum Stillstand kommen soll. Integration von (14) nach der Zeit
liefert:
mgr − µ( ab + 1)RF
ż =
t + C1
ΘA
r + mr
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 6
SS 2012
mit der Anfangsbedingung
ż(t = 0) =! v0 ⇒ C1 = v0
⇒ ż(t) =
mgr − µ( ab + 1)RF
Forderung:
ż(t = T ) = 0 ⇒
ΘA
r
+ mr
t + v0
mgr − µ( ab + 1)RF
ΘA
r
+ mr
(15)
T + v0 = 0
Umformung nach F :
A
v0 ( Θr + mr) + mgrT
F =
µ( ab + 1)RT
(16)
(b)
Nun ist der Weg zu berechnen, den die Masse m während des Bremsvorgangs zurücklegt. Aus Gleichung (15) folgt
nach nochmaliger Integration nach der Zeit für den Ort:
z(t) =
mgr − µ( ab + 1)RF t2
+ v0 t + C2
ΘA
2
r + mr
(17)
mit der Anfangsbedingung z(t = 0) = 0 ⇒ C2 = 0.
Es ergibt sich der Bremsweg“ zu:
”
mgr − µ( ab + 1)RF T 2
z(t = T ) =
+ v0 T
ΘA
2
r + mr
(18)
Nach Einsetzen von F aus Gleichung (16) in (18):
1
z(t = T ) = − v0 T + v0 T
2
1
= v0 T
2
(c) Freischnitt für den Gleichgewichtszustand
FAz
II
F̃N
FAx
(19)
(20)
R
r
S
I
F̃R
G2
S
mg
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9.Übungsblatt
Starrkörperkinetik I
- S. 7
SS 2012
Gleichgewichtsbedingung am Körper II:
X
M A = 0 ⇒ F̃R R − Sr = 0
(21)
X
(22)
Gleichgewichtsbedingung am Körper I:
Einsetzen von Gleichung (22) in (21) ergibt:
Fz = 0 ⇒ S = mg
⇒ F̃R = mg
r
R
(23)
Für die Haftreibkraft F̃R ist nun der Haftreibungskoeffizient µ0 zu verwenden. Es gilt:
F̃R = µ0 F̃N
(24)
Die Normalkraft F̃N ist analog zu Aufgabenteil (a) entsprechend Gleichung (5) zu berechnen:
a
⇒ F̃N = F̃ ( + 1)
b
(23) und (25) in (24) einsetzen:
r
a
= µ0 F̃ ( + 1)
R
b
mgr
F̃ =
µ0 R( ab + 1)
(25)
mg
(26)