Theorieaufgaben LA =
Werbung

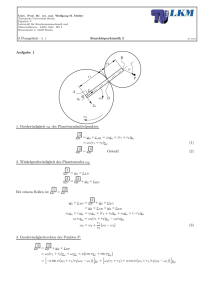
Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin Theorieaufgaben 1. Geben Sie die kinetische Energie des Körpers an, der an zwei masselosen Pendelstützen aufgehängt ist. E kin (ϕ̇) = ϕ, ϕ̇ l l S Θ(S) , M Geg.: ϕ̇, l, M; Θ(S) 2. Gegeben ist ein Feder-Masse-System: c2 c1 c3 c4 welches ersetzt wird durch cers m m Berechnen Sie die Ersatzfedersteifigkeit cers . cers = Geg.: c1 , c2 , c3 , c4 3. Die starre Kugel (m, ΘS ) dreht sich mit der Winkelgeschwindigkeit ω, ihr Schwerpunkt bewegt sich mit der Geschwindigkeit v (ebenes Problem). Geben Sie den Drehimpuls der Kugel in Bezug auf den ω ruhenden Punkt A an! Geg.: a, b, m, ΘS , v, ω LA = b v A a Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 4. Ein Massepunkt stößt auf eine glatte Ebene, wobei v − und v + die Geschwindigkeiten unmittelbar vor bzw. nach dem Stoß sind. Bitte kreuzen Sie die richtigen Aussagen an. α x g β v− v+ v+ = v− v+ < v− v+ > v− β = α β < α β > α e=1 0<e<1 e=0 y 5. Ein stehender Güterwagen (m1 = 20t) wird durch einen anderen Güterwagen (m2 = 30t) mit einer Geschwindigkeit von v2 = 5km/h gerammt. Welche Geschwindigkeit ergibt sich, wenn die Wagen nach dem Zusammenstoß miteinander zusammengekoppelt sind? Reibung soll vernachläßigt werden. 6. Ein Hammer bestehend aus Kopf (Trägheitsmoment Θz,1 , M, Masse M) und Stiel (Trägheitsmoment Θz,2 , m, Masse m). Bestimmen Sie das Massenträgheitsmoment des Hammers bzgl. des Punktes A. ey b Θz,1, M (A) Θz,Hammer = . . . ex ez Θz,2 , m A l Geg.: M, m, l, b, Θz,1, Θz,2 (jeweils bzgl. des Teilkörperschwerpunkts) 7. Wie groß sind die Massenträgheitsmomente des skizzierten Systems bezüglich der Achsen x, y, z? (Die Massen sind als Massenpunkte zu betrachten.) y Θx = z m l m l l Θy = x l m Θz = m Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 8. Bestimmen Sie das Massenträgheitsmoment Θ(A) bezüglich des festen Drehpunktes A. Drücken Sie Θ(A) ausschließlich durch die gegebenen Größen m1 , m2 und l aus. ϕ A m dünner homogener 1 Stab l 2 Θ(A) = S Punktmasse m2 l 4 l 4 9. Eine Punktmasse m trifft mit der Geschwindigkeit v0 auf dem Boden auf und springt anschließend in die Höhe h. Bestimmen Sie die Stoßzahl e. g h e = ... v0 m Geg.: m, g, h, v0 10. An einer Masse m greift eine richtungstreue Kraft F an. Berechnen Sie die Arbeit, welche die Kraft auf den Weg ABC leistet. WABC = F A B m b ey ex a C Geg.: F , a, b 11. Zwei Punktmassen umkreisen einander im festen Abstand 2R mit konstanter und gleicher Geschwindigkeit. Ein kompletter Umlauf dauert T . m Geben Sie die kinetische Energie E an. Geg.: m, R, T E= m 2R Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 12. Geben Sie die Maßeinheiten folgender Größen in den Einheiten 1, kg, m und s an: Drehmoment M . . . Winkelgeschwindigkeit ω. . . schwere Masse m. . . Gravitationskonstante g. . . (g tritt im Gravitationsgesetz auf der Erde FG = mg auf.) 13. Eine Punktmasse m bewegt sich auf einer schiefen Ebene. Kann man ẋ(x) mit dem Energiesatz berechnen? Bitte kreuzen Sie jeweils eine Antwort pro Kasten an. x x g m c µ= g m c µ 6= 0 0 α Ja α Ja Nein x Nein x g g m m d µ= Ja 0 µ= c 0 α α Ja Nein Nein 14. Eine lineare Feder mit Steifigkeit c wird um den Wert ∆x vorgespannt. Dann schießt die Feder die Masse m nach oben. Dabei entspannt sich die Feder. Bis in welche maximale Höhe h fliegt die Kugel (ohne Luftwiderstand)? g m NN Geg.: m, c, ∆x, g. um ∆x vorgespannt h= Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 15. Ein Voll- und ein Hohlzylinder mit gleicher Masse m, gleicher ρ1 Länge L, mit gleichem Aussenradius R und homogener Dichte S1 werden auf einer schiefen Ebene plaziert und rollen anschließend (ohne Anfangsgeschwindigkeit) schlupffrei vom gleichen 1 Startpunkt ab. Für die Schwerpunktsgeschwindigkeiten gilt nach gleicher Lauflänge: vS,2 , vS,1 denn es gilt: ΘS,1 (=, <, >) ρ2 r R g S2 R 2 ΘS,2 . (=, <, >) Geg.: R, r, L, g 16. Eine Masse m wird im Erdschwerefeld g mit x(t) = at2 + b sin (ωt) abgeseilt. Bestimmen Sie die Kraft FSeil im stets straffen Seil. FSeil g x(t) m FSeil = . . . Geg.: a, b, ω, m, g, x(t) = at2 + b sin (ωt) 17. Von welchen Parametern hängt die gedämpfte Eigenkreisfrequenz eines linearen Systems bei kleinen Auslenkungen? x(t) c m Anfangsgeschwindigkeit v0 Masse m Federsteifigkeit c Phasenwinkel ϕ Amplitude A Lehrsches Dämpfungsmaß D d 18. Zwei Systeme I und II werden aus der Ruhe beschleunigt. Welche der folgenden Relationen gilt? Tragen Sie ein! <, >, = ẍ1 Geg.: m, g, F = mg ẍ2 m m g g x1 I x2 m II F = mg Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin F 19. Geben Sie die Leistung P an, die die Kraft F an dem mit der Geschwindigkeit v bewegten Karren leistet. v P = α 20. Eine homogene Walze rollt verlustfrei aus der Ruhe heraus eine Rampe der Höhe h0 hinunter. Im anschließenden senkrechten freien Flug erreicht sie die Höhe h. g h h0 Welche Aussage ist richtig? Bitte kreuzen Sie an. h = h0 h = 32 h0 h= √ 2gh0 21. Der Arbeitssatz kann aufgeschrieben werden als W1→2 = Ekin1 − Ekin0 . W1→2 ist die Arbeit, die am System auf dem Weg von 0 nach 1 geleistet wird. Welche Kräfte gehen bei dieser Formulierung des Arbeitssatzes in W1→2 ein? (bitte ankreuzen) nur konservative Kräfte nur nicht-konservative Kräfte konservative und nicht-konservative Kräfte nur Gewichtskräfte Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 22. Eine dünne homogene Stange der Masse m und Länge l gleitet reibungsfrei mit ihren Endpunkten A, B auf zwei zueinander senkrecht stehenden Wänden. (a) Konstruieren Sie den Momentanpol zum Zeitpunkt t=0 wenn der Winkel α = 45◦ beträgt! y x A l S O α g B (b) Berechnen Sie mit Hilfe der Eulerschen Starrkörpergleichung den Betrag der Geschwindigkeit des Punktes A für den Zeitpunkt t=0, wenn die Winkelgeschwindigkeit der Leiter um den Momentanpol ω L = ωez beträgt! Geg.: m, g, l 23. Geben Sie die Maßeinheiten folgender Größen ausschließlich in den Einheiten 1, kg, m und s an: Größe Maßeinheit Massenträgheitsmoment Θ(S) Stoßzahl e potentielle Energie E pot Erregerkreisfrequenz Ω 24. An einem masselosen und undehnbaren Seil hängt die Masse M. Das Seil wird über eine masselose Scheibe umgelenkt zur Masse m, die auf einem reibungsfreien Untergrund gleiten kann. Mit welcher Beschleunigung sinkt die Masse M? g m masselos masselos µ=0 M ÿ = y, ẏ, ÿ Univ. Prof. Dr. rer. nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 25. Zwei Systeme I und II werden aus der Ruhe beschleunigt. Es gibt kein Schlupf zwischen den Seilen und den homogenen Kreisscheiben (Radien R bzw. r). Welche der folgenden Relationen gilt? <, >, = ẍ1 Geg.: m, g, F , r, R, R > r ẍ2 m x1 I R, m F g m x2 II r, m F g