Θ , Ω M , Ω , g , c , k ϕ
Werbung

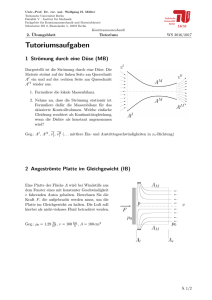
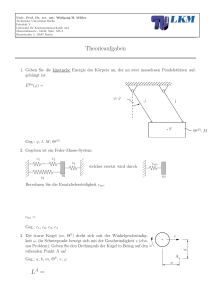
Univ. Prof. Dr. rer nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 8 . Übungsblatt Energiemethoden WS 2012/2013 Tutoriumaufgaben 1) Das skizzierte System wird durch das Moment M (t ) zum Schwingen angeregt. Der Strömungswiderstand der Kugel ist proportional zur Geschwindigkeit mit dem Widerstandkoeffizienten k . Alle anderen Widerstände, die Masse der Umlenkrolle sowie der hydrostatische Auftrieb der Kugel sollen vernachlässigt werden. Die nicht dehnbaren Seile bleiben immer x = 0 entspannt. gespannt. Die Feder ist bei ~ a) Stellen Sie die EULER-LAGRANGEsche Bewegungsgleichung des Systems (in der Variable ~ x ) auf. b) Berechnen Sie die statische Ruhelage xstat für den Fall M (t ) = 0 . c) Transformieren Sie die Bewegungsgleichungen auf Schwingungen um die statische Rux − xstat helage x = ~ Geg.: m1 , m2 , Θ S , M (t ) = M 0 cosΩ t , M 0 , Ω , g , c , k ϕ1 c M (t ) ex S ey g r R ~ x1 m1 , Θ S k reines Rollen m2 y1 2) Ein Rütteltisch T bewegt sich reibungsfrei unter dem Antrieb der Unwuchtmasse m durch einen Motor mit einer konstanter Geschwindigkeit Ω . Stellen Sie die EULER-LAGRANGEsche Bewegungsgleichunge des Systems auf. Geg.: M , m , Ω, d , c, l1 , h1 , h2 , r , g Univ. Prof. Dr. rer nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 8 . Übungsblatt Energiemethoden WS 2012/2013 Hausaufgabe 3) Ein Schlitten (Masse M ) ist, wie in der Abbildung zu sehen, mit einer Feder der Steifigkeit c verbunden und gleitet reibungsfrei auf dem Untergrund. Auf dem Schlitten befindet sich eine walze (Radius r , Masse m ), die wieder über eine Feder der Steifigkeit c mit der Schlittenwand verbunden ist. Die Bewegung der Walze soll rein rollend ablaufen. Berechnen Sie mithilfe der Lagrange-Gleichungen 2. Art die Bewegungsgleichungen des Systems. Geg.: m , M , Θ S1 , r , c ϕ ey ex 1 r c S m , Θ S1 c 2 x M