Tutoriumsaufgaben 1. Das Sonnenrad 1 bewege sich mit der

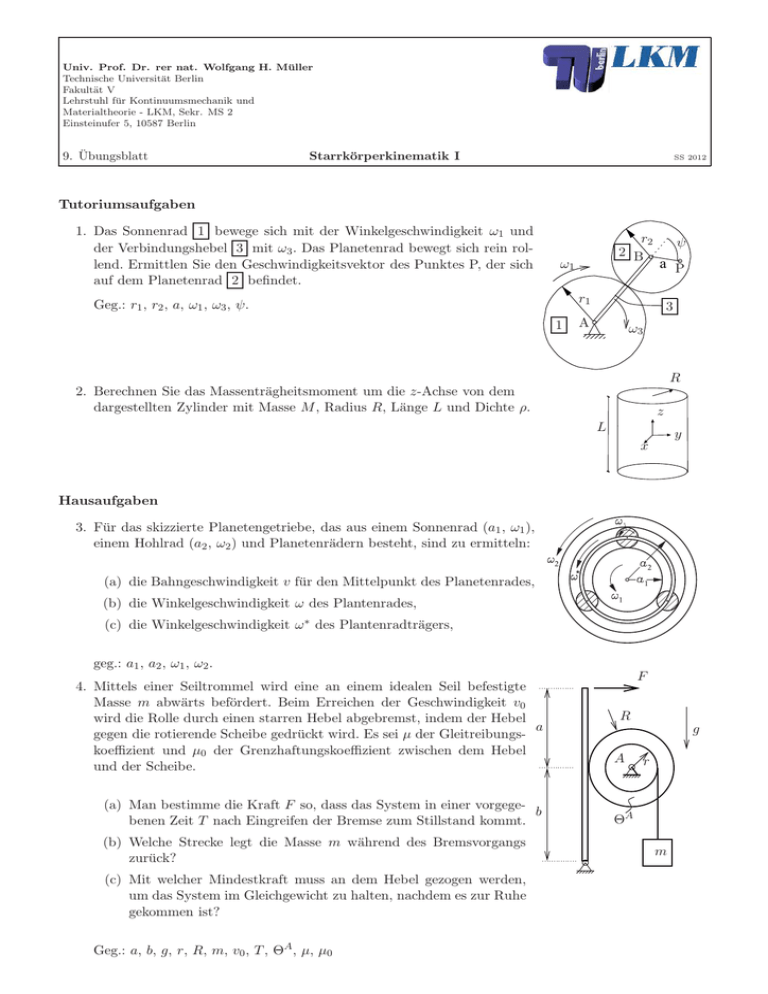
Univ. Prof. Dr. rer nat. Wolfgang H. Müller
Technische Universität Berlin
Fakultät V
Lehrstuhl für Kontinuumsmechanik und
Materialtheorie - LKM, Sekr. MS 2
Einsteinufer 5, 10587 Berlin
9. Übungsblatt
Starrkörperkinematik I
SS 2012
Tutoriumsaufgaben
1. Das Sonnenrad 1 bewege sich mit der Winkelgeschwindigkeit ω1 und
der Verbindungshebel 3 mit ω3 . Das Planetenrad bewegt sich rein rollend. Ermittlen Sie den Geschwindigkeitsvektor des Punktes P, der sich
auf dem Planetenrad 2 befindet.
r2
2 B
ω1
ψ
a P
r1
Geg.: r1 , r2 , a, ω1 , ω3 , ψ.
1
3
A
ω3
R
2. Berechnen Sie das Massenträgheitsmoment um die z-Achse von dem
dargestellten Zylinder mit Masse M , Radius R, Länge L und Dichte ρ.
z
L
y
x
Hausaufgaben
3. Für das skizzierte Planetengetriebe, das aus einem Sonnenrad (a1 , ω1 ),
einem Hohlrad (a2 , ω2 ) und Planetenrädern besteht, sind zu ermitteln:
(a) die Bahngeschwindigkeit v für den Mittelpunkt des Planetenrades,
(b) die Winkelgeschwindigkeit ω des Plantenrades,
(c) die Winkelgeschwindigkeit ω ∗ des Plantenradträgers,
geg.: a1 , a2 , ω1 , ω2 .
4. Mittels einer Seiltrommel wird eine an einem idealen Seil befestigte
Masse m abwärts befördert. Beim Erreichen der Geschwindigkeit v0
wird die Rolle durch einen starren Hebel abgebremst, indem der Hebel
a
gegen die rotierende Scheibe gedrückt wird. Es sei µ der Gleitreibungskoeffizient und µ0 der Grenzhaftungskoeffizient zwischen dem Hebel
und der Scheibe.
(a) Man bestimme die Kraft F so, dass das System in einer vorgegeb
benen Zeit T nach Eingreifen der Bremse zum Stillstand kommt.
(b) Welche Strecke legt die Masse m während des Bremsvorgangs
zurück?
(c) Mit welcher Mindestkraft muss an dem Hebel gezogen werden,
um das System im Gleichgewicht zu halten, nachdem es zur Ruhe
gekommen ist?
Geg.: a, b, g, r, R, m, v0 , T , ΘA , µ, µ0
F
R
g
A
r
ΘA
m