Die geradlinig gleichförmige Bewegung
Werbung

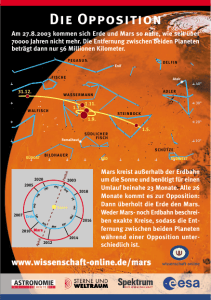
12-1-1-6 Newtonsches Gravitationsgesetz Was hält die Planeten auf ihrer Umlaufbahn? Die Schüler sehen einen Film zum Gravitationsgesetz: http://www.kunischschule.com/12-1-1-6%20Gravitationsgesetz.swf Gravitationsgesetz Zwei beliebige Massen ziehen sich gegenseitig mit der Massenanziehungskraft an: FG 6,67 10 11 m1 m2 mit F G || r 2 r m3 heißt Gravitationskonstante. kg s 2 r Sind die Massen m1 oder m 2 kugelförmig, so ist der Abstand r zu den Massenmittelpunkten zu wählen. Bei den Überlegungen zum Gravitationsgesetz ließ Newton sich von den Keplerscherschen Gesetzen leiten. Wir vollziehen die Herleitung des Gravitationsgesetzes mit Hilfe der StEx-Methode nach: http://www.kunischschule.com/PDF-Dokumente/12/12-1-1-6-StEx.pdf Das Gravitationsgesetz ist im gesamten Kosmos gültig. Newton hat mit dieser Forderung der 2000 Jahre alte Behauptung von Aristoteles, dass zwischen „irdischer” und „überirdischer” Physik zu unterscheiden sei, widersprochen. Ein über zahlreiche Generationen hinweg weit verbreitetes Weltbild wurde durch diesen genialen Gedanken revolutioniert. Selbst Kepler formulierte seine Gesetze noch als Resultat seiner Suche nach einer „Weltharmonik”, die für unser Sonnensystem gültig ist, unabhängig von allgemeingültigen Regeln. Die geforderte Allgemeingültigkeit des Gravitationsgesetzes verleitete Newton zu einer Betrachtung, die heute als „Mondrechnung” bekannt. In seinen Gedanken bildete die Erde den Zentralkörper, um den andere reale oder virtuelle Objekte wie Mond oder Äpfel kreisen können wie Planeten um die m m Sonne. Auf diese Objekte wirkt dann die Erdanziehungskraft G Obekt 2 Erde . r Wir vollziehen die Mondrechnung mit Hilfe der StEx-Methode. http://www.kunischschule.com/PDF-Dokumente/12/12-1-1-6-StEx2.pdf Newtons Mondrechnung ergab die korrekte Umlaufdauer des Mondes TMond 27d . Die Umlaufdauer des Mondes ist somit ein Resultat der allgemeinen physikalischen Gesetze, was Newton bestärkte, an die Richtigkeit seiner Überlegungen zu glauben. Die Schüler sehen einen Film über Isaac Newton: http://www.kunischschule.com/12-1-1-6%20Newton.swf 1. Welche Massenanziehung besteht zwischen einem 75kg schweren Mann und einer 50kg schweren Frau, die sich im Abstand von 1m befinden? 2. Newton war zu seiner Zeit noch nicht in der Lage, die Gravitationskonstante zu bestimmen, da die Gravitation zwischen zwei Labormassen sehr klein ist und die Erdmasse noch nicht bekannt war. 1797 führte der britische Naturwissenschaftler Henry Cavendish (1731 - 1810) mit einer Gravitationsdrehwaage die erste Bestimmung der Gravitationskonstanten durch. Mit der Kenntnis der Gravitationskonstanten war Cavendish in der Lage, die Erde zu „wiegen”. Beschreibe den Aufbau und die Messung mit einer Gravitationswaage und bestimme mit Hilfe der Gravitationskonstanten die Masse der Erde. 3. a. Erläutere, dass sich ein geostationärer Satellit (oder Synchronsatellit) ohne Antrieb über einem bestimmten Punkt der Erde aufhalten kann. b. Berechne die Höhe, in der sich geostationäre Satelliten aufhalten. c. Begründe, dass in Deutschland Parabolantennen für Satellitenempfang nach Süden ausgerichtet werden. 4. Die erdnächsten Satelliten haben eine Höhe von etwa 200km über dem Erdboden. Berechne deren Umlaufzeit. 5. (Saarländische Abiturprüfung 2011) Zusätzliche Angaben: Masse des Mars 6,42 10 23 kg Durchmesser des Mars 6800km 1 In naher Zukunft wollen Forscher zum Mars reisen, um den Planeten zu erkunden. Eine solche Reise kann jedoch nicht zu einem beliebigen Zeitpunkt erfolgen. Während die Erde die Sonne auf einer Bahn in 150 Millionen Kilometer Abstand umkreist und dazu 365 Tage braucht, benötigt der Mars für eine Runde 687 Tage. Gut alle zwei Jahre überholt der Heimatplanet den Mars also. Nur dann ist der Mars von der Erde aus bzw. die Erde vom Mars aus erreichbar. Gehen Sie im Folgenden von der stark vereinfachten Annahme aus, dass beide Planetenbahnen kreisförmig sind. 2.1 Geben Sie das dritte Keplersche Gesetz an und berechnen Sie anhand einer Skizze den minimalen und maximalen Abstand von Erde und Mars. 2.2 Während die Astronauten den Mars erkunden, umkreist ihr Basisschiff den Mars. Bestimmen Sie die Geschwindigkeit des Raumschiffs in einer Höhe von 100km über der Planetenoberfläche sowie die Zeit für eine Umrundung des Planeten in dieser Höhe. 2.3 Der Mond Phobos umrundet den Planeten Mars auf einer elliptischen Bahn, wobei sich der Planet Mars in einem Brennpunkt der Ellipse befindet. Markieren Sie in der Skizze den Bahnpunkt, in dem die Bahngeschwindigkeit von Phobos maximal ist, und erläutern Sie den physikalischen Hintergrund. 1. Aus dem Newtonschen Gravitationsgesetz FG m1 m2 folgt FG 2,5 10 7 N . 2 r 2. Siehe Film dieser Stunde zum Newtonschen Gravitationsgesetz. Es ergibt sich die Erdmasse mErde 6 10 24 kg . 3. a. Ein geostationärer Satellit muss sich mit derselben Frequenz um die Drehachse der Erde drehen wie die Erde selbst, damit er immer über demselben Punkt der Erde stehen kann. Zudem muss sich der gewählte stationärer Punkt über dem Äquator befinden, da der Satellit sich nicht nur um die Rotationsachse der Erde, sondern auch um den Mittelpunkt der Erde drehen muss. mErde mSatellit mSatellit 2 r mit r2 m3 6,67 10 11 , mErde 6 10 24 kg und TErde 24h kg s 2 Daraus folgt r 42300km . b. Wir verwenden r ist der Abstand vom Erdmittelpunkt. Der Satellit muss sich also etwa 36000km über der Erdoberfläche befinden. c. Die Parabolspiegel werden in Richtung der geostationären Satelliten ausgerichtet, die sich über dem Äquator - von Europa aus gesehen also im Süden - befinden. mErde mSatellit mSatellit 2 r mit r 6400km 200km 6600km folgt 2 r 1 1,18 10 3 T 89 min s 4. Aus 5. 2.1 (6 Punkte) 3. Keplersches Gesetz: Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen der großen Bahnhalbachsen. 2 2 2 3 TMars TErde rErde TMars 3 3 3 rMars rErde 2 rMars rErde 3 2 2 TErde TErde TMars rMars rMars 150 10 m 3 9 687d 2 365d 2 Damit gilt: Maximaler Abstand Erde-Mars Minimaler Abstand 229 10 9 m 229Mio..Km d max rErde rMars (150 229)Mio.km 379Mio.km Erde-Mars d min rErde rMars (229 150)Mio.km 79Mio.km Wegen der elliptischen Umlaufbahn der Planeten ist der tastsächliche maximale Abstand ca. 6% größer und der tatsächliche minimale Abstand um ca. 30% geringer als der jeweilige unter der Annahme kreisförmiger Umlaufbahnen berechnete Wert. 2.2 (5 Punkte) Die Newtonsche Gravitationskraft wirkt als Zentripetalkraft: mBasisschiff mMars v2 mit r RMars 100km r mBasisschiff r2 mMars 6,67 10 11 m 3 kg 1 s 2 6,42 10 23 kg 3,5kms1 v 6 r 3,5 10 m Formelsammlung: v 2 r T T 2r 2 3,5 10 6 m 105 60s 105 min v 3,5 10 3 ms 1 2.3 (2 Punkte) Das 2. Keplersche Gesetz besagt, dass der Fahrstrahl zwischen Zentralkörper und umlaufendem Körper in gleichen Zeiten gleiche Flächen überstreicht. Da der Fahrstrahl beim geringsten Abstand von Mars und Phobos am kleinsten ist, muss an dieser Stelle die Bahngeschwindigkeit am größten sein.