Übung 3: Die generische Klasse „BinärerSuchbaum“ in Java 1

Algorithmen und Datenstrukturen
Übung 3: Die generische Klasse „BinärerSuchbaum“ in Java 1
Datenelemente der Klasse BinaererSuchbaum
Das einzige Datenelelement in dieser Klasse ist die Wurzel vom Typ
BinaerBaumknoten. Die Klasse „BinaerBaumknoten“ ist allgemein sichtbar.
Der binäre Suc hbaum setzt voraus, daß alle Datenelemente der Baumknoten in eine
Ordnungsbeziehung gebracht werden können. Eine generische Klasse für einen
binären Suchbaum erfordert daher ein Interface, das Ordnungsbeziehungen
zwischen Daten eines Datenbestands festlegt. Diese Eigenschaft besitzt das
Interface Comparable
public interface Comparable
{
int compareTo(Comparable rs)
}
Durch die Definition eines Interface wird der zugehörige Referenztyp erzeugt, der wie
andere Datentypen eingesetzt werden kann.
Methoden der Klasse BinaererSuchbaum
Die öffentlich zugänglichen, sichtbaren Methoden rufen private, rekursive Methoden
auf:
Die private Methode „elementAt“ gibt eine Referenz zurück, die auf den Baumknoten verweist, in
dem ein bestimmtes Datenelement gespeichert ist.
Das Auffinden eines Datenelements im binären Suchbaum besorgt: private BinaerBaumknoten
find(Comparable x, BinaerBaumknoten b);
Das Auffinden des größten bzw. kleinsten Datenelements im binären Suchbaum übernehmen:
private BinaerBaumknoten findMax(BinaerBaumknoten b);
private BinaerBaumknoten findMin(BinaerBaumknoten b);
Das Einfügen eines Knoten in den binären Suchbaum übernimmt: private BinaerBaumknoten
insert(Comparable x, BinaerBaumknoten b);
Duplikate können beim Einfügen durch ein spezielles Feld im Baumknoten behandelt werden, das die
doppelten Vorkommen zählt.
Das Löschen eines Baumkoten übernimmt private BinaerBaumknoten remove(Comparable
x, BinaerBaumknoten b);
Beim Entfernen sind 3 Fälle zu unterscheiden:
1. Der zu entfernende Knoten ist ein Blattknoten. Das Entfernen dieses Knoten kann direkt erfolgen.
2. Der zu entfernende Knoten hat einen Nachfolger. Hier wird vom Elternknoten des zu entfernenden
Knoten ein Link auf den Nachfolger des zu entfernenden Knoten gesetzt.
1 Vgl. PR42000
1
Algorithmen und Datenstrukturen
6
2
6
8
1
4
2
8
1
4
3
3
3. Der zu entfernende Knoten hat 2 Nachfolger. Hier könnte eine allgemeine Strategie für das
Entfernen des Knoten so lauten:
- Ersetze den Inhalt des Datenelements durch den Inhalt des kleinsten Datenelements des rechten
Teilbaums. Dieser Baumknoten kann leicht gefunden werden.
- Das Datenelement mit dem kleinsten Inhalt vom rechten Teilbaum des zu entfernenden Baumknoten
ist dann leer, der zugehörige Baumknoten kann deshalb rekursiv entfernt werden. Da der Knoten mit
dem kleinsten Inhalt des Datenelements keine linken Nachfolger besitzt, ist diese Art des Entfernens
einfach
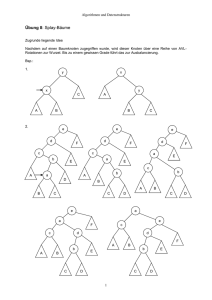
Bsp.: Entfernen des Knotens mit dem Datenelement 2
6
2
6
8
1
5
3
3
8
1
5
3
4
4
Test: Klasse BinaerSuchbaumTest
Aufgaben: Ersetze die rekursiven Methoden durch Methoden, die Iterationen anstatt Rekursionen
verwenden.
2
Algorithmen und Datenstrukturen
Lösungen
// Elementarer Knoten eines binaeren Baums, der nicht ausgeglichen ist
// Der Zugriff auf diese Klasse ist nur innerhalb eines Verzeichnisses
// bzw. Pakets moeglich
class BinaerBaumknoten
{
// Instanzvariable
protected BinaerBaumknoten links;
protected BinaerBaumknoten rechts;
public Comparable daten;
// linker Teilbaum
// rechter Teilbaum
// Dateninhalt der Knoten
// Konstruktor
public BinaerBaumknoten(Comparable datenElement)
{
this(datenElement, null, null );
}
public BinaerBaumknoten(Comparable datenElement,
BinaerBaumknoten l,
BinaerBaumknoten r)
{
daten
= datenElement;
links
= l;
rechts
= r;
}
public BinaerBaumknoten getLinks()
{
return links;
}
public BinaerBaumknoten getRechts()
{
return rechts;
}
}
// Freier binaerer Intervallbaum
// Generische Klasse fuer einen unausgeglichenen binaeren Suchbaum
//
// Konstruktor: Initialisierung der Wurzel mit dem Wert null
//
// **********oeffentlich zugaengliche
Methoden*************************************
// void insert( x )
--> Fuege x ein
// void remove( x )
--> Entferne x
// Comparable find( x )
--> Gib das Element zurueck, das zu x passt
// Comparable findMin( ) --> Rueckgabe des kleinsten Elements
// Comparable findMax( ) --> Rueckgabe des groessten Elements
// boolean isEmpty( )
--> Return true if empty; else false
// void makeEmpty( )
--> Entferne alles
// void printTree( )
--> Ausgabe der Binaerbaum-Elemente in sortierter
Folge
// void ausgBinaerBaum() --> Ausgabe der Binaerbaum-Elemente um 90 Grad
vers.
/*
* Implementiert einen unausgeglichenen binaeren Suchbaum.
* Das Einordnen in den Suchbaum basiert auf der Methode compareTo
*/
public class BinaererSuchbaum
{
3
Algorithmen und Datenstrukturen
// Private Datenelemente
/* Die Wurzel des Baums */
private BinaerBaumknoten root;
// Oeffentlich zugaengliche Methoden
/*
* Konstruktor.
*/
public BinaererSuchbaum()
{
root = null;
}
/*
* Einfuegen eines Elements in den binaeren Suchbaum
* Duplikate werden ignoriert
*/
public void insert( Comparable x )
{
root = insert(x, root);
}
/*
* Entfernen aus dem Baum. Falls x nicht da ist, geschieht nichts
*/
public void remove( Comparable x )
{
root = remove(x, root);
}
/*
* finde das kleinste Element im Baum
*/
public Comparable findMin()
{
return elementAt(findMin(root));
}
/*
* finde das groesste Element im Baum
*/
public Comparable findMax()
{
return elementAt(findMax(root));
}
/*
* finde ein Datenelement im Baum
*/
public Comparable find(Comparable x)
{
return elementAt(find(x, root));
}
/*
* Mache den Baum leer
*/
public void makeEmpty()
{
root = null;
}
/*
* Test, ob der Baum leer ist
*/
public boolean isEmpty()
{
return root == null;
}
/*
* Ausgabe der Datenelemente in sortierter Reihenfolge
4
Algorithmen und Datenstrukturen
*/
public void printTree()
{
if( isEmpty( ) )
System.out.println( "Baum ist leer" );
else printTree( root );
}
/*
* Ausgabe der Elemente des binaeren Baums um 90 Grad versetzt
*/
public void ausgBinaerBaum()
{
if( isEmpty() )
System.out.println( "Leerer baum" );
else
ausgBinaerBaum( root,0 );
}
// Private Methoden
/*
* Methode fuer den Zugriff auf ein Datenelement
*/
private Comparable elementAt( BinaerBaumknoten b )
{
return b == null ? null : b.daten;
}
/*
* Interne Methode fuer das Einfuegen in einen Teilbaum
*/
private BinaerBaumknoten insert(Comparable x, BinaerBaumknoten b)
{
/* 1*/
if( b == null )
/* 2*/
b = new BinaerBaumknoten( x, null, null );
/* 3*/
else if( x.compareTo( b.daten ) < 0 )
/* 4*/
b.links = insert( x, b.links );
/* 5*/
else if( x.compareTo( b.daten ) > 0 )
/* 6*/
b.rechts = insert( x, b.rechts );
/* 7*/
else
/* 8*/
; // Duplikat; tue nichts
/* 9*/
return b;
}
/*
* Interne Methode fuer das Entfernen eines Knoten in einem Teilbaum
*/
private BinaerBaumknoten remove(Comparable x, BinaerBaumknoten b)
{
if( b == null )
return b;
// nichts gefunden; tue nichts
if( x.compareTo(b.daten) < 0 )
b.links = remove(x, b.links );
else if( x.compareTo(b.daten) > 0 )
b.rechts = remove( x, b.rechts );
else if( b.links != null && b.rechts != null ) // Zwei Kinder
{
b.daten = findMin(b.rechts).daten;
b.rechts = remove(b.daten, b.rechts);
}
else
b = ( b.links != null ) ? b.links : b.rechts;
return b;
}
/*
* Interne Methode zum Bestimmen des kleinsten Datenelements im Teilbaum
*/
5
Algorithmen und Datenstrukturen
private BinaerBaumknoten findMin(BinaerBaumknoten b)
{
if (b == null)
return null;
else if( b.links == null)
return b;
return findMin(b.links );
}
/*
* Interne Methode zum Bestimmen des groessten Datenelements im Teilbaum
*/
private BinaerBaumknoten findMax( BinaerBaumknoten b)
{
if( b != null )
while( b.rechts != null )
b = b.rechts;
return b;
}
/*
* Interne Methode zum Bestimmen eines Datenelements im Teilbaum.
*/
private BinaerBaumknoten find(Comparable x, BinaerBaumknoten b)
{
if(b == null)
return null;
if( x.compareTo(b.daten ) < 0)
return find(x, b.links);
else if( x.compareTo(b.daten) > 0)
return find(x, b.rechts);
else
return b;
// Gefunden!
}
/*
* Internae Methode zur Ausgabe eines Teilbaums in sortierter Reihenfolge
*/
private void printTree(BinaerBaumknoten b)
{
if(b != null)
{
printTree(b.links);
System.out.print(b.daten);
System.out.print(' ');
printTree( b.rechts );
}
}
/*
* Ausgabe des Binaerbaums um 90 G rad versetzt
*/
private void ausgBinaerBaum(BinaerBaumknoten b, int stufe)
{
if (b != null)
{
ausgBinaerBaum(b.links, stufe + 1);
for (int i = 0; i < stufe; i++)
{
System.out.print(' ');
}
System.out.println(b.daten);
ausgBinaerBaum(b.rechts, stufe + 1);
}
}
}
6
Algorithmen und Datenstrukturen
public class BinaererSuchbaumTest
{
// Test program
public static void main( String [] args )
{
// Test Nr. 1
BinaererSuchbaum b = new BinaererSuchbaum();
final int ZAHLEN = 4000;
final int LUECKE = 37;
System.out.println(
"Pruefung... (keine weiteren Ausgaben bedeutet Erfolg)");
for( int i = LUECKE; i != 0; i = (i + LUECKE) % ZAHLEN)
b.insert( new Integer( i ) );
for(int i = 1; i < ZAHLEN; i+= 2 )
b.remove( new Integer( i ) );
if (ZAHLEN < 40)
b.printTree( );
if( ((Integer)(b.findMin( ))).intValue( ) != 2 ||
((Integer)(b.findMax( ))).intValue( ) != ZAHLEN - 2 )
System.out.println( "FindMin oder FindMax -Fehler!" );
for( int i = 2; i < ZAHLEN; i+=2 )
if( ((Integer)(b.find( new Integer( i ) ))).intValue( ) != i )
System.out.println( "Find Fehler Nr.1!" );
for( int i = 1; i < ZAHLEN; i+=2 )
{
if( b.find( new Integer( i ) ) != null )
System.out.println( "Find error2!" );
}
// Test Nr.2
BinaererSuchbaum b1 = new BinaererSuchbaum();
for (int i = 0; i < 10; i++)
{
// Erzeuge eine Zahl zwischen 0 und 100
Integer r = new Integer((int)(Math.random()*100));
b1.insert(r);
}
System.out.println("Inorder-Durchlauf");
b1.printTree();
System.out.println();
System.out.println("Baumdarstellung um 90 Grad versetzt");
b1.ausgBinaerBaum();
System.out.print("Kleinster Wert: ");
System.out.print(((Integer)(b1.findMin())).intValue());
System.out.println();
System.out.print("Groesster Wert: ");
System.out.print(((Integer)(b1.findMax())).intValue());
System.out.println();
for (int i = 0; i < 10; i++)
{
// Erzeuge eine Zahl zwischen 0 und 100
Integer r = new Integer((int)(Math.random()*100));
if ( b1.find(r) != null )
{
b1.remove( r );
}
// else System.out.println(r.intValue() + " nicht gefunden");
}
b1.ausgBinaerBaum();
// Test Nr. 3
BinaererSuchbaum b2 = new BinaererSuchbaum();
for (int i = 0; i < 20; i++) // 20 Zusfallsstrings speichern
{
String s = "Zufallszahl " + (int)(Math.random() * 100);
7
Algorithmen und Datenstrukturen
b2.insert(s);
}
b2.printTree(); // Sortiert wieder ausdrucken
}
}
8