Genial Mathematik 1 - Bildungsverlag Lemberger
Werbung
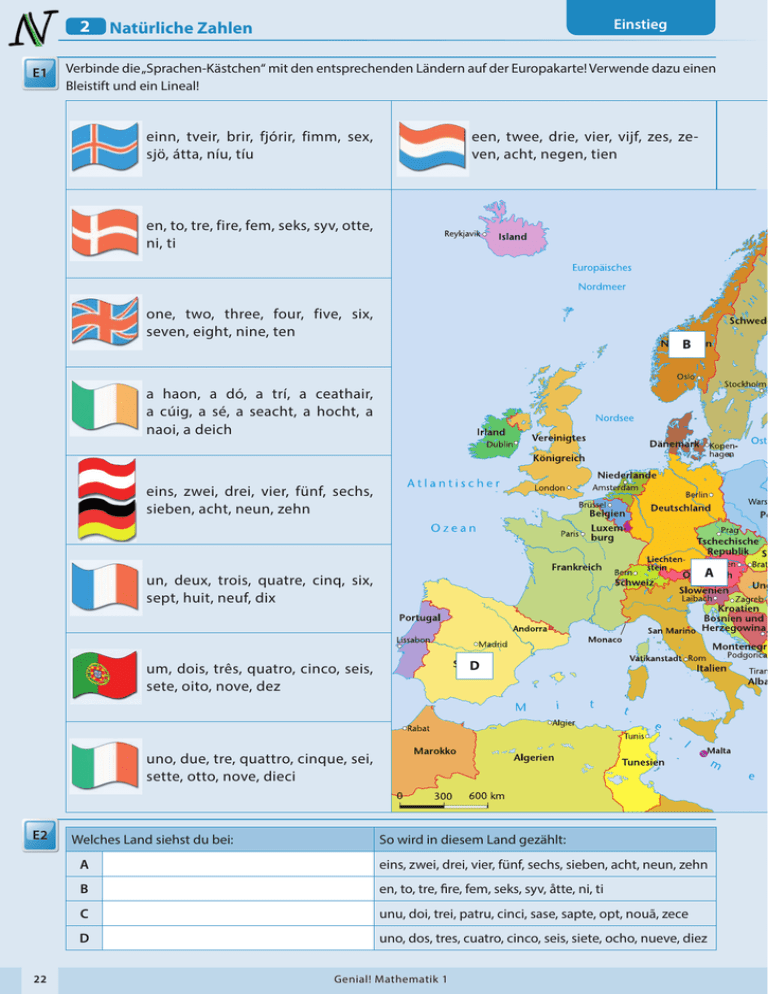
2 E1 Einstieg Natürliche Zahlen Verbinde die „Sprachen-Kästchen“ mit den entsprechenden Ländern auf der Europakarte! Verwende dazu einen Bleistift und ein Lineal! einn, tveir, brir, fjórir, fimm, sex, sjö, átta, níu, tíu een, twee, drie, vier, vijf, zes, zeven, acht, negen, tien en, to, tre, fire, fem, seks, syv, otte, ni, ti one, two, three, four, five, six, seven, eight, nine, ten B a haon, a dó, a trí, a ceathair, a cúig, a sé, a seacht, a hocht, a naoi, a deich eins, zwei, drei, vier, fünf, sechs, sieben, acht, neun, zehn A un, deux, trois, quatre, cinq, six, sept, huit, neuf, dix D um, dois, três, quatro, cinco, seis, sete, oito, nove, dez uno, due, tre, quattro, cinque, sei, sette, otto, nove, dieci E2 22 Welches Land siehst du bei: So wird in diesem Land gezählt: A eins, zwei, drei, vier, fünf, sechs, sieben, acht, neun, zehn B en, to, tre, fire, fem, seks, syv, åtte, ni, ti C unu, doi, trei, patru, cinci, sase, sapte, opt, nouã, zece D uno, dos, tres, cuatro, cinco, seis, siete, ocho, nueve, diez Genial! Mathematik 1 2 Einstieg Natürliche Zahlen Die Flaggen neben den Sprachen helfen dir, das richtige Land zu finden! en, två, tre, fyra, fem, sex, sju, åtta, nio, tio yksi, kaksi, kolme, neljä, viisi, kuusi, seitsemän, kahdeksan, yhdeksän, kymmenen viens, divi, trĩs, četri, pieci, seši, septini, astoni, devini, desmit один, два, три, четьіре, пять, шесть, семь, восемь, девять, десять jeden, dwa, trzy, cztery, pięć, sześć, siedem, osiem, dziewięć, dziesięć едно, две, три, четири, пет, шест, седем, осем, девет, десет një, dy, tre, katër, pesëe, gjashtëe, shtatë, tetë, nëntë, dhjetë C bir, iki, üç, dört, bes, alti, yedi, sekiz, dokuz, on ένα, δύο, τρια, τέσσερα, πέντε, έξι, εφτά, οχτώ, εννέα, δέκα In wie vielen Sprachen (außer Deutsch) kannst du bis 10 zählen? E3 Welche Sprachen sind das? E4 Wie viele Kinder deiner Klasse können in zwei anderen Sprachen (außer Deutsch) bis 10 zählen? E5 Genial! Mathematik 1 23 3 M1 2 Natürliche Zahlen 3. Addition und Subtraktion Diese Zeichen „übersetze“ ich so: = < M2 > Ich kann und gerade Zahlen (z. B. unterscheiden, ungerade Zahlen (z. B. ) weil: M3 Jede Zahl hat einen Vorgänger und einen Nachfolger. Vorgänger Zahl Nachfolger So finde ich Vorgänger und Nachfolger: 5 20 149 M4 So arbeite ich mit der Stellenwerttafel: T H Z E 2 1 4 5 4 3 So heißt die Zahl 1 509 613 Darauf muss ich beim Ablesen achten: Darauf muss ich beim Eintragen achten: 24 Check-in Methode Genial! Mathematik 1 3. Addition und Subtraktion Check-in Wissen 2 Natürliche Zahlen 1 Schreibe die Zahl neben die Angabe! 6T 5H 4Z 3E W1 M HT ZT T H 3 I1, H2 Z 2a E 2b W2 a) Wie heißt die Zahl? b) Wie heißt die Zahl, wenn die Tausenderstelle mit der Einerstelle vertauscht wird? I1, H1, H2 3a Kreuze die richtigen Zahlen an! W3 a)4H 2Z 1E b)8H 4E 412 84 241 804 421 840 3b I1, H2 4a Bilde aus den Ziffern 4, 1, 6, 9, 3 a) die größte fünfstellige Zahl! 4b W4 b) die kleinste fünfstellige Zahl! I1, H1, H2 5a Setze die Zahlenfolge fort! W5 a) 301, 311, 321, b) 1 290, 1 305, 1 320, 5b , , I1, H2 6a Max rundet auf Tausender: W6 a) Schreibe die größte Zahl auf, die Max auf 8 000 runden kann! 6b b) Schreibe die kleinste Zahl auf, die Max auf 8 000 runden kann! c) Erkläre, wie du bei a) und b) gedacht hast! 6c I1, H1, H2, H4 Kreuze die richtig gelösten Beispiele im Balken an! Genial! Mathematik 1 25 2.6 Runden und Schätzen Beispiele I1 Bei diesem Eishockeyspiel waren 4 011 Fans. In den Sportnachrichten wurde die gerundete Zahl 4 000 verwendet. Warum ist das sinnvoll? 89 H4 Im täglichen Leben werden Zahlen oft gerundet (bessere Übersicht, Merkbarkeit, Vergleichbarkeit). Eine Tafel Schokolade kostet 79 Cent. Das sind rund 80 Cent. 79 ≈ 80 „rund“ Vor dem Runden unterstreiche den Stellenwert, auf den gerundet werden soll. Die Ziffer rechts daneben gibt an, ob abgerundet oder aufgerundet wird. Bei 0, 1, 2, 3, 4 runde ab. Bei 5, 6, 7, 8, 9 runde auf. 122 € ≈ 120 € 389 € ≈ 390 € Abrunden oder aufrunden? Ordne die Zahlen zu! 19, 22, 47, 36, 51, 63, 85, 74, 92, 28, 39, 25 Runde ab bei den ­Ziffern 0, 1, 2, 3 und 4 30 30 31 32 33 34 35 36 abrunden 37 38 39 Runde auf bei den ­Ziffern 5, 6, 7, 8 und 9 H3 40 aufrunden Abrunden 22, 90 Aufrunden 19, Runde auf Zehner! Kennzeichne den Stellenwert! 91 z. B. 12 ≈ 10 18 ≈ 20 H2, H1 a) 11 ≈ c) 42 ≈ e) 114 ≈ g) 455 ≈ b) 37 ≈ d) 58 ≈ f) 216 ≈ h) 289 ≈ Runde auf Hunderter! Kennzeichne den Stellenwert! 92 z. B. 319 ≈ 300 471 ≈ 500 H2, H1 a) 314 ≈ c) 748 ≈ e) 5 307 ≈ g) 8 787 ≈ b) 483 ≈ d) 801 ≈ f) 10 490 ≈ h) 9 430 ≈ Runde auf … 93 a) Zehner: 15, 32, 41, 57, 63, 78, 99, 104 c) Tausender: 5 250, 4 870, 6 712, 6 312, 9 900, 6 783 b) Hunderter: 290, 2 150, 881, 2 800, 3 415, 4 771 d) Zehntausender: 12 500, 29 400, 16 702, 43 493 Genial! Mathematik 1 H2 41 2.6 Runden und Schätzen Beispiele I1 96 H3, H2 a)Beschrifte die Bundesländer Österreichs in der Österreichkarte! Bemale ihre Flächen in unterschiedlichen Farben. b)Runde den Flächeninhalt der Bundesländer auf Tausender! Vorarlberg. . . . . . . . . . . . . . . . 2 601 km2 ≈ Steiermark. . . . . . . . . . . . . . . 16 392 km2 ≈ Tirol. . . . . . . . . . . . . . . . . . . . . 12 648 km2 ≈ Niederösterreich. . . . . . . . . 19 178 km2 ≈ Salzburg. . . . . . . . . . . . . . . . . . 7 154 km2 ≈ Burgenland. . . . . . . . . . . . . . . 3 965 km2 ≈ Kärnten. . . . . . . . . . . . . . . . . . . 9 536 km2 ≈ Wien . . . . . . . . . . . . . . . . . . . . . . . 415 km2 ≈ Oberösterreich. . . . . . . . . . . 11 982 km2 ≈ Quelle: www.wko.at c)Ordne die Bundesländer der Größe nach! Beginne mit mit dem Bundesland mit der kleinsten Fläche! Suche im Internet die Einwohnerzahlen der Bundesländer! Schreibe sie auf, runde auf HT und ordne sie der Größe nach! Beginne mit dem Bundesland mit der geringsten Einwohnerzahl! Der Unterschied zum genauen Wert ist der Rundungsfehler. Gib den Rundungsfehler an! 97 484 ≈ 480 R = 4 1 517 ≈ 2 000 R = 3 105 ≈ 3 000 R = 379 ≈ 380 R = 1 399 ≈ 1 000 R = 4 670 ≈ 5 000 R = 516 ≈ 520 R = 3 709 ≈ 4 000 R = 4 264 ≈ 4 000 R = H3, H2 98 Runde sinnvoll! a) Der Umfang der Erde am Äquator beträgt etwa 40 076 km. H1, H2 b) Das Volumen der Erde beträgt etwa 1 083 Mrd km3. c) Die Masse der Erde beträgt etwa 5 972 Trilliarden t. d) Wie schwer sind alle ÖsterreicherInnen zusammen? Begründe deine Schätzung! Genial! Mathematik 1 43 2 Thema Entwicklung der Zahlen Die Menschen zählten zuerst Mitglieder der Sippe und Dinge aus ihrer Umgebung. Die Zahl der Tiere oder Gegenstände wurde später auch in Hölzer eingeritzt und damit dokumentiert. T1 Was können Menschen im linken Bild zählen? Die Ägypter beschäftigten sich viel mit Rechnen und Baukunst. Hier siehst du ihre Zahlzeichen. T1 Suche in deinem Atlas Ägypten! 1 2 3 4 5 6 7 8 9 10 100 1000 10 000 Welche Zahlen sind hier abgebildet? Addiere die Zahlzeichen! = = T3 = = Unsere Ziffern stammen aus Indien und wurden von den Arabern nach Europa gebracht. Daher nennen wir sie arabische Ziffern. 4 321 ist eine Zahl. Sie wird aus den Ziffern 4, 3, 2 und 1 gebildet. T4 Suche in deinem Atlas Indien und Europa. indisch 3. Jh. v. Chr. indisch 8. Jh. westarabisch 11. Jh. europäisch 16. Jh. Neuzeit 20. Jh. Genial! Mathematik 1 47 2 T5 Thema Römische Zahlen Die Römer verwendeten vor etwa 2 000 Jahren Zahlzeichen, die du heute noch in Häuserinschriften oder auf Uhren findest. Alle Zahlen im römischen Zahlensystem werden aus 7 Zahlzeichen gebildet. Suche in deinem Atlas Italien (Rom)! I=1 C = 100 V=5 D = 500 X = 10 M = 1000 L = 50 Regeln für die römischen Zahlen I, X, C und M werden höchstens dreimal hintereinander geschrieben. V, L und D werden höchstens einmal in einer Zahl verwendet. Zahlzeichen hintereinander geschrieben werden addiert. III = 3, CC = 200, VI = 6, LX = 60 Ein kleines Zahlzeichen vor einem größeren wird subtrahiert. IV = 4, IX = 9 T6 Schreibe die Zahlen mit römischen Zahlzeichen! 1 T7 T8 48 2 3 4 5 6 7 8 9 Schreibe mit römischen Zahlzeichen! 17 = 24 = 158 = 212 = 1 919 = 189 = 1 650 = 1 709 = 1 971 = 54 = 49 = 144 = 411 = 3 219 = 2 705 = 2 015 = 690 = 99 = Schreibe mit unseren Ziffern! XII = VIII = XXIV = CCL = CXC = DLV = MDCC = CDXIII = MDCCXI = MMCI = CCXLIX = CXL = MDL = LXVI = XXXVII = MCX = IX = MMDL = CXL = CCXI = XXIX = XC = XXI = XVII = Genial! Mathematik 1 10 2 Thema T10 T9 Römische Spielereien Mein Geburtsdatum: Tag Monat T11 Jahr 20 . . MM __ Schreibe die Jahreszahl der Hausinschrift auf! Wie spät ist es? Ein Füllrätsel für alle, die mit römischen Zahlen umgehen können. Deine Aufgabe ist es, die Zahlen I, II, VI, XII, XXX so in das Feld einzutragen, dass die waagrechten und senkrechten Rechnungen stimmen. T12 Du brauchst nun Streichhölzer, um die Aufgaben zu lösen. Kannst du durch Umlegen von 2 Streichhölzern die Rechnung richtig stellen? T13 Jetzt darf nur mehr 1 Hölzchen verändert werden! T14 Genial! Mathematik 1 49 2 50 Kompetenz Lernen®: Schuhstatistik I4 Genial! Mathematik 1 Bildungsstandards Bildungsstandards 2 Kompetenz Lernen®: Schuhstatistik a) Arbeite mit deiner Sitznachbarin oder deinem Sitznachbarn: Sammelt zunächst alle Informationen aus dem Comic. Wie viele Kinder gehen in Käthes und Rudis Klasse? Wie viele Kinder tragen welche Schuhgröße? Legt in eurem Heft eine Tabelle an! b)Rudi möchte ein Balkendiagramm zeichnen, in dem die Anzahl der Schuhgrößen übersichtlich dargestellt ist. Könnt ihr Rudis Darstellung vervollständigen? Schuhgröße I4 B1 Anzahl K1, H1 34 35 36 … … K1, H1 6 5 4 3 2 1 34 35 36 37 38 39 40 41 a)Käthe überlegt: „Meine Größe ist die, die am öftesten vorkommt. Das heißt, das muss auch die Durchschnittsgröße sein … Aber das rechne ich zuerst einmal nach!" Welches Ergebnis erhält Käthe? b)Käthe ist misstrauisch: „Wenn wir niemanden in der Klasse mit Schuhgröße 41 hätten und nur 19 Kinder wären, dann wäre die Durchschnittsgröße ungefähr …" Rechne wieder nach! Was bedeutet das Ergebnis nun für Käthes erste Vermutung? Formuliere deine Schlussfolgerung schriftlich! Max geht in die Parallelklasse und schaut bei Käthe und Rudi vorbei: „Ah Rudi - du zeichnest ein Diagramm der Schuhgrößen? Und Käthe, das ist bei euch die Durchschnittsgröße? So ein Zufall, bei uns auch!" Rudi grübelt: „Hmmm… ohne zu wissen wie viele Kinder welche Schuhgröße haben, kann ich nichts eindeutig zeichnen, aber ich könnte zumindest raten. In die Parallelklasse gehen 24 Kinder und die Durchschnitssgröße ist die gleiche wie in unserer Klasse, also… " Könnt ihr Rudi helfen? Arbeitet zu zweit und zeichnet ein Diagramm, in dem eine mögliche Anzahl der Schuhgrößen in der Parallelklasse abzulesen ist! Max kommt wenig später mit einem von ihm erstellten Diagramm zurück: „Schau, Rudi, wir haben eine Umfrage gemacht, wer in unserer Klasse wie viele Paar Schuhe besitzt. Mehr als 7 Paare hatte niemand, und nur ein Paar auch nicht!" Betrachte das Diagramm genau und versuche, folgende Fragen zu beantworten: Was ist auf der waagrechten Achse und was ist auf der senkrechten Achse eingezeichnet? Wie viele Kinder haben weniger als 4 Paar Schuhe? Kann man ablesen, wie viele Kinder in Max' Klasse gehen? Erkläre genau wie und warum! Wie viele Paar Sommerschuhe haben die Kinder in Max' Klasse insgesamt? Wie viele Paar Schuhe haben die Kinder in Max' Klasse im Durschschnitt? B2 K1, H2 K3, H4 B3 K2, H1 B4 K4, H3 8 7 6 5 4 3 2 1 0 Genial! Mathematik 1 1 2 3 4 5 6 7 51 2 M1 Check-out Methode Natürliche Zahlen Wenn ich von Zahlen den Mittelwert errechne, gehe ich so vor: z. B.: 7, 15, 17 Meine Rechnungen: M2 Trage jeweils die Zahlen 4 und 7 ein! 0 5 0 5 Folgendes muss ich beim Eintragen beachten: M3 Beim Runden von Zahlen muss ich beachten: 0, 1, 2, 3, 4 5, 6, 7, 8, 9 Runde auf Z! Runde auf H! 74 119 Meine Überlegungen beim Runden 52 Genial! Mathematik 1 2 Check-out Wissen W1 Natürliche Zahlen Herr Maier stoppt seine Arbeitszeit in der Küche: Mo … 37 min, Di … 42 min, Mi … 11 min. Berechne die mittlere Arbeitszeit während dieser 3 Tage! 1 I4, H1, H2 2a Ergänze: a) W2 V Z b) N 99 V Z N c) V Z 124 N 2b 1 498 2c I1, H2 3 Welche Zahlen sind markiert? W3 0 1 I1, H3 Ordne die gegebenen Zahlen. Beginne mit der größten Zahl! W4 4 3 849, 9 439, 4 938, 8 394, 3 948 I1, H2 5a Schreibe als Zahl an: W5 a) 4T 3H 2Z 3E b) 1ZT 6H 3E I1, H1 6a Runde auf den in der Klammer angegebenen Stellenwert: W6 a) 1 928 (Z) b) 8 354 (H) 5b c) 8 374 (T) 6b I1, H2 6c 7 W7 Gib die Teiler von 40 an! W8 Schreibe die ersten 5 Vielfachen von 6 auf! I1, H3 8 I1, H2, H3 9 Markiere die Zahlen 40, 70, 110 und 140 am Zahlenstrahl! W9 0 10 50 I1, H1 W10 10a Schreibe mit Ziffern an: a) Dreihundertfünfzigtausendeinhundertsiebzehn b) Fünftausendsiebenhundertachtundneunzig I1, H1 11a Setze das entsprechende Zeichen ∣ oder ∤ ! W11 a) 5 55 b) 11 99 c) 4 11b 73 I1, H3 W12 Gib drei natürliche Zahlen an, die durch 11 teilbar sind und zwischen 70 und 100 liegen! W13 10b Wie viele Vielfache von 12 liegen zwischen 58 und 90? 11c 12 I1, H1, H3 13 I1, H1, H3 Kreuze die richtig gelösten Beispiele im Balken an! Genial! Mathematik 1 53