Die Frage nach dem mysteriösen Faktor 1-exp(-t/ta

Prof. Dr. R. Kessler, FH-Karlsruhe, http://www.home.hs-karlsruhe.de/~kero0001 , E-Funktion.doc, Seite 1/1
Was ist eigentlich die berühmte Exponentialfunktion e
x
Eine der wichtigsten Funktionen ist die sogenannte Exponentialfunktion
y = ex
In der Technik kommt sie „pausenlos“ vor. Leider aber selten mal in einem Gymnasium.
y= „e hoch x“, geschrieben
Wer hat sie erfunden?? Natürlich Meister Leonhard Euler. Drum heißt die Zahl „e“ nach ihm .
Der Zahlenwert dieser wichtigen Zahl ist e= 2.7182818...
Bei Computerprogrammen, so auch in Tephys und Matlab und Pascal und Basic und C und C++ etc. schreibt man
statt der obigen Exponentialform y=exp(x), also exp(1) = e= 2.7182818...
Wie ist Euler darauf gekommen, eine solche Funktion zu erfinden??
Wir spielen jetzt mal Euler und wollen uns in seine Erfindungsgedanken versetzen:
Wir suchen eine Funktion, nennen wir sie zunächst mal E(x), deren Ableitung nach x die Funktion selber ist.
Also hat die noch unbekannte Funktion die Eigenschaft dE/dx = E. Dies allein genügt noch nicht zur Definition. Also
Zusatz-Definition: Bei x=0 soll E=1 sein, also E(0) =1.
Also haben wir (genau genommen) eine DGL ( also mal wieder!), nämlich dE/dx=E mit „Anfangswert“ E(0)=1.
Nehmen wir Tephys, um zumindest die Zahlenwerte und auch das Schaubild dieser Funktion E(x) zu finden.
Einziger Nachteil von Tephys: die „unabhängige“ Variable heißt bei Tephys t (=Zeit). Also dE/dt=E
Tephys-Progrämmle zum Berechnen und Zeichnen von E(t) . Wichtig: Startwert von E ist 1:
1¦ E=E+E*dt
2¦ t=t+dt
Einfacher geht’s wohl kaum noch! Damit wir auch erkennen, wie gut das so berechnete E(t) mit der echten eFunktion e= exp(t) übereinstimmt, rechnen wir dies auch aus und lassen auch die Abweichung dif = e-E berechnen.
Damit haben wir unser erstes Programm:
--- D:\KUELLMAR\EFUN1.TXT ------1¦ E = E+E*dt { Diese simple Gleichung ist “UNSER” Zugang zur unbekannten “e-Funktion” }
2¦ e = exp(t) { Das ist die „richtige“ e-Funktion}
3¦ dif = e-E
{ das ist unser Fehler}
4¦ t = t+dt
{ die Schrittweite dt wird wohl eine wichtige Rolle spielen!! }
Um Das Programm Tephys noch besser auszunutzen, wird im nachfolgenden Tephys-Programm EfUN2.TXT
zusätzlich die gleiche DGL noch mit der viel genaueren Methode „Runge-Kutta“ gelöst,
Ergebnis ist die Funktion Er.
Der Runge-Kutta-Algorithmus ist relativ kompliziert, wenn man ihn „direkt“ programmieren muss. In Tephys
ist er dagegen sehr einfach „aufzurufen“: Zwischen die Zeilen DGL=0 und END=0 werden die zu lösenden
DGLn eingetippt in der Form y=rk(y’), wobei y’ die zeitliche Ableitung der zu suchenden Funktion y(t) ist. Da
unsere hier behandelte DGL die Gestalt hat dy/dt= y, heißt das y=rk(y).
Ausgeführt im folgenden Algorithmus als Er = rk(Er) (s. Zeile 5)
------- D:\KUELLMAR\ EFUN2.TXT -------1¦ E = E+E*dt { E = die gesuchte “e-Funktion”, gelöst mit “Tephys-Algorithmus”}
2¦ e = exp(t) { e = die „richtige“ Exponentialfunktion}
3¦ dif = e-E
{ dif = Abweichung }
4¦ DGL = 0
{ DGL=0 Startzeile für „Runge-Kutta-Algorithmus“ }
5¦ Er = rk(Er) { Er = die gesuchte Lösung der DGL dEr/dt = Er }
6¦ END = 0
{ END=0 Endzeile für „Runge-Kutta-Algorithmus“ }
7¦ difrk = e-Er { difrk =Abweichung}
8¦ t = t+dt
{ Schrittweite dt, wichtig für Genauigkeit, vgl. anschließende Bilder }
Bei dieser Gelegenheit sei aus der Tephys-Hilfe Tepinfo.pas die Passage über Runge-Kutta hier „eingefügt“:
Prof. Dr. R. Kessler, FH-Karlsruhe, http://www.home.hs-karlsruhe.de/~kero0001 , E-Funktion.doc, Seite 2/2
RUNGE-KUTTA { Beispiel: Feder-Masse-System, 2 Freiheitsgrade }
DGL=0
{ in Klammern die Dgln }
F0=A0*ja(t-t1)*ja(t2-t)
x1=rk(v1)
{ dx1/dt=v1 }
x2=rk(v2)
{ dx2/dt=v2 }
v1=rk((F0-D1*x1+D2*(x2-x1)-R1*v1)/m1) { m1*dv1/dt = F0-D1*x1...-R1*v1 }
v2=rk((D2*(x1-x2)-R2*v2)/m2)
{ m2*dv2/dt = D2*(x1-x2)-R2*v2 }
END=0
t=t+dt
Anschließend einige Tephysbilder mit obigem Programm EFUN2.TXT, Variation der Schrittweite dt
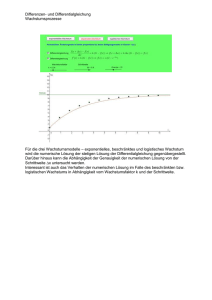
Bild F1: Die Kurven für E, für den exakten Wert e und für den Runge-Kutta-Wert Er haben den gleichen Nullpunkt
und den gleichen y-Faktor (s. die obere Kurve dieses Bildes). Man erkennt, dass im Rahmen der
„Zeichengenauigkeit“ die drei Kurven aufeinanderliegen. Unsere simple Berechnung der Exponentialfunktion mit
dem Tephys-Algorithmus E=E+E*dt liefert also „auf Anhieb“ sehr gute Werte! Die Tabelle im Bild zeigt
genaueres, mit den beiden Kurven dif und difrk zeigt die Tabelle die „Rechenfehler“ bei der gewählten Schrittweite
dt=0.001.
Bild F2: Schrittweite dt= 0.00001, also 100 mal kleiner als in Bild F1, y-Faktor(=10000) bei der Kurve dif 10 mal
größer also in Bild F1. Infolge der 100 mal kleineren Schrittweite dt ist E etwa 100 mal genauer geworden (vgl.
die Tabellen in den Bildern). Erstaunlicherweise ist bei der Runge-Kutta-Methode die Übereinstimmung deutlich
weniger gut als bei der größeren Schrittweite!.
Prof. Dr. R. Kessler, FH-Karlsruhe, http://www.home.hs-karlsruhe.de/~kero0001 , E-Funktion.doc, Seite 3/3
Bild F3: Schrittweite 10 mal kleiner als in Bild F2. Wieder ist bei E die Genauigkeit gestiegen (um Faktor 10
verglichen mit 10-facher Schrittweite, Bild F2). Und auch hier setzt sich die Tendenz durch, dass Ungenauigkeit der
Runge-Kutta-Methode größer geworden. ist!
Der Grund für diese unerwartete Ungenauigkeit der Runge-Kutta-Methode dürften „Rundungsfehler“ sein: Da
Tephys mit begrenzter Stellenzahl der Zahlenwerte rechnet, ist notwendig die letzte Ziffer einer Zahl schon ein
„gerundeteter“ Wert. Kleinere Schrittweite dt bewirkt, dass mehr solche gerundeten Zahlen addiert oder subtrahiert
oder multipliziert werden. Die dabei entstehenden Zahlen sind immer wieder gerundet. Folglich ist der Einfluß der
Rundungsfehler umso größer, je kleiner die Schrittweite dt ist, weil dann umso häufiger mit gerundeten Zahlen
operiert wird. – Bei dem einfachen Tephys-Algorithmus E = E+ E*dt machen sich die Rundungsfehler noch
nicht bemerkbar, weil Verkleinerung der Schrittweite dt die Rechengenauigkeit noch verbessert (z.B. in der 5.
Dezimalstelle), die Rundungsfehler treten aber erst in der (z.B.) 15. Dezimalstelle auf.
Eine andere Methode, sich mit der
Exponentialfunktion vertraut zu machen:
Diese Methode wird in manchen Lehrbüchern behandelt.
Wieder ist dE/dx=E
--> dE= E*dx
E(0)=1.
Wir vergrößern x in Schritten dx , berechnen die Änderung dE und daraus den jeweils „neuen“ Wert von E aus dem
„alten“ Wert: E= Ealt + dE . Den im neuen Wert E vorkommenden Faktor 1+dx klammern wir aus und erhalten
dadurch eine Formel für E(x), die (beim Grenzübergang für kleine dx) übergeht in die mathematische Form E(x) =e^x,
oder mit Formeleditor geschrieben:
E ( x ) = e x dabei ist die neue Zahl e diese berühmte Zahl e= 2.7182818...
Kleine Tabelle:
Nr n x
0
0
1
dx
2
2*dx
dE=E*dx
0
1*dx
(1+dx)*dx
3
((1+dx)^2)*dx
4
.
.
n
3*dx
4*dx
n*dx
((1+dx)^3)*dx
((1+dx)^(n-1))*dx
E = Ealt + dE
1
1+dx
1+dx +(1+dx)*dx = (1+dx)*(1+dx)
{ Faktor 1+dx wurde ausgeklammert}
= (1+dx)^2
{^2 heißt „hoch zwei“ }
(1+dx)^2+ ((1+dx)^2)*dx = (1+dx)*(1+dx)^2
=(1+dx)^3 {wieder wurde Faktor 1+dx ausgeklammert}
(1+dx)^3 +((1+dx)^2)*dx = (1+dx)*(1+dx)^3
=(1+dx)^4 {wieder wurde Faktor 1+dx ausgeklammert}
(1+dx)^(n-1) +((1+dx)^(n-1))*dx
= (1+dx)*(1+dx)^(n-1)
= (1+dx)^n{wieder wurde Faktor 1+dx ausgeklammert}
Man hat also eine „Folge“ erhalten:
Für x= n*dx ist E(n) = (1+dx)^n, n = 0,1,2,....
Gesucht ist der Grenzwert für n gegen unendlich.
Prof. Dr. R. Kessler, FH-Karlsruhe, http://www.home.hs-karlsruhe.de/~kero0001 , E-Funktion.doc, Seite 4/4
Es ist x = n*dx, also n = x/dx, dann ist
E(x)= (1+dx)^(x/dx)
a B* D = ( a B ) D
= ((1+dx)^(1/dx))^x
{beachte:
= Ek^x mit Ek = ((1+dx)^(1/dx).
}
Diese schönen Formeln mit dem Formeleditor geschrieben:
E ( x ) = (1 + dx )
x
dx
1
dx
= ((1 + dx ) ) x = E k
x
. Wichtig daran sind zwei Dinge: Erstens ein „Rezept“ zum
Berechnen des Zahlenwertes der Konstante Ek als Grenzwert, zweitens, dass unsere unbekannte Funktion E(x) als
„Exponentialfunktion“ auftauscht: E(x)= Ek^x gelesen „Ek hoch x“
Hierin soll E k eine „Konstante“ sein, deren Wert wir aber noch nicht wissen.
Ek ergibt sich als Grenzwert für dx sehr klein.
Setzen wir dx als sehr klein an: dx =1/N mit N sehr groß, dann ist Ek(N) = (1+1/N)^N
Oder mit Formeleditor:
E k ( N ) = (1 +
1 N
)
N
Für N gegen unendlich ergibt sich die berühmte Zahl „e“ : Ek --> e= 2.7182818... (s.o.).
Es hatte sich ergeben E(x)= Ek^x. Ersetzen wir jetzt endlich unsere vorübergehende Zahl Ek durch „e“, so hat man
also
E(x) = e^x, gelesen: „e hoch x“ oder mit Formeleditor:
E ( x) = e x
Die oben „hergeleitete“ Formel für die Zahl e, nämlich e = Grenzwert von (1+1/N)^N (für N gegen unendlich)
„konvergiert“ allerdings sehr schlecht. Mit dem Taschenrechner kann man das probieren:
N
(1+1/N)^N
„wahrer“ Wert ist e=2.7182818..
.........................................................
10
2.5937...
{ Abweichung schon in 1.Stelle nach Komma}
100
2.7048...
{ Abweichung in 2. Nachkommastelle }
1000
2.7169...
{ Abweichung in 3. Nachkommastelle }
10000
2.7181459
{ Abweichung in 4. Nachkommastelle }
100000
2.7182682
{ Abweichung in 5. Nachkommastelle }
1E6
2.7182805 ( N= 1 Million,
Abweich. in 6. Nachkommastelle )
1E7
2.7182817 ( N= 10 Millionen, Abweich. in 7. Nachkommastelle )
1E8
2.7182818 ( N= 100 Millionen. Jetzt erst „fast“ richtig, aber stimmt
noch immer nicht, denn e hat unendlich viele Stellen:)
Mit Matlab auf 15 Stellen gerechnet: exp(1) = 2.71828182845905 ( und die Zahl e geht immer noch weiter!)
Exponentialfunktion als Taylor-Reihe:
Die sog. Taylor-Reihe einer Funktion f(x) ist ( für die „Entwicklungs-Stelle“ x=0)
f(x) = f(0) + f’(0)*x /1! +f’’(0)*x^2 /2! + f’’’(0) * x^3 /3! + f’’’’(0)* x^4 /4!… oder mit Formeleditor
x
x2
x3
xn
f ( x ) = f ( 0) + ⋅ f ' ( 0) +
⋅ f ' ' ( 0) +
⋅ f ' ' ' (0) + ... +
⋅ f ( n ) (0) + ....
1!
2!
3!
n!
Wobei die „Fakultät n!“ bedeutet: z.B. 3! = 1*2*3=6, 4! = 1*2*3*4=24, 0!=1
Wie ist Herr Taylor auf diese Formel gekommen?
Ganz einfach: gesucht ist eine „Potenzreihen-Entwicklung“ einer Funktion f(x), die „möglichst gut“ mit der
gegebenen Funktion f(x) übereinstimmt
Versuchen wir das „nach-zu-erfinden“: Wir schreiben die Funktion als „Potenzreihe“ mit zunächst noch
unbekannten Konstanten a0, a1, a2,...
f(x)=a0 + a1*x + a2 * x^2 + a3 * x^3 + a3 * x^4 +.... (Zur Erinnerung: x^4 heißt „x hoch 4“ )
Den Wert a0 finden wir sofort: wird x=0 gesetzt so bleibt f(0) = a0,
Machen wir die erste Ableitung von f(x) und auch von der Potenzreihe:
... f’(x) = a1 + a2*2* x +a3*3*x^2 + a4*4*x^3 + a5*5*x^4 +...
also
a0 = f(0).
Prof. Dr. R. Kessler, FH-Karlsruhe, http://www.home.hs-karlsruhe.de/~kero0001 , E-Funktion.doc, Seite 5/5
Setzen wir wieder x=0, so bleibt f’(0) = a1,
Man ahnt, wie es weitergeht: zweite Ableitung ergibt
f’’(x) = 2*a2 + a3*3*2*x + a4 * 4*3*x^2 + a5 * 5*4*x^3+ ...
x=0 gesetzt liefert f’’(0) = 2*a2,
also
also
Dritte Ableitung: f’’’(x) = a3*3*2 + a4* 4*3*2 *x + a5 * 5*4*3* x^2 + ...
f’’’(0) = a3* 3*2, also a3 = f’’’(0) / (2*3) oder mit Fakultätszeichen:
Offenbar geht das munter so weiter und man erhält z.B.
a1=f’(0)
a2 = f’’(0) / 2
a3 = f’’’(0) / 3!
a7 = f’’’’’’’(0) / 7!
Damit haben wir Herrn Taylors Reihe neu erfunden.
Jetzt die Taylor-Reihe der Exponentialfunktion:
Tun wir so, als wüssten wir von der Exponentialfunktion „nur“ die Definition als DGL: gesucht Funktion E(x) mit
DGL dE/dx = E, Startwert E(0)=1. Da definitionsgemäß die Ableitung von E wieder E ist, sind auch sämtliche
Ableitungen von E gleich E selbst: z.B. die 4. Ableitung: E’’’’ = E’’’ = E’’ = E’ = E. Folglich haben alle Ableitungen
bei x=0 den Wert E(0) = 1. Folglich können wir die Taylor-Reihe der gesuchten Funktion E(x) sofort
hinschreiben:
E ( x) = 1 +
x x2 x3
xn
+
+
+ ... +
+ ....
1! 2! 3!
n!
Natürlich wieder Tephys:-------- D:\KUELLMAR\EXP_1.TXT
1¦ e = exp(t)
{ e = „echte“ Exponentialfunktion}
2¦ t3 = t*t*t
{ t3 = t^3 }
3¦ t4 = t3*t
{ t4=t^4 }
4¦ t5 = t4*t
{ t5 = t^5 }
5¦ t6 = t5*t
6¦ t7 = t6*t
7¦ t8 = t7*t
8¦ t9 = t8*t
{ t8 = t^8 = „t hoch 8“}
9¦ t10 = t9*t
10¦ t11 = t10*t
11¦ t12 = t11*t
12¦ t13 = t12*t { t12 = t^12 = „t hoch 13“}
13¦ E8 = 1+t+t*t/2+t3/6+t4/fak(4)+t5/fak(5)+t6/fak(6)+t7/fak(7)+t8/fak(8)
{ E8 = Taylor-Reihe der Exponentialfunktion bis zum Glied „t hoch 8“}
14¦ E13 = E8+t9/fak(9)+t10/fak(10)+t11/fak(11)+t12/fak(12)+t13/fak(13)
{ E13 = Taylor-Reihe der Exponentialfunktion bis zum Glied „t hoch 13“}
15¦ dif8 = e-E8 { Abweichung wahrer Wert e von der Taylorreihe bis zum Glied x hoch 8 }
16¦ dif13 = e-E13 { Abweichung wahrer Wert e von der Taylorreihe bis zum Glied x hoch 13 }
17¦ t = t+dt {}
Fig. F4: Taylor-Reihe der Exponentialfunktion und Fehler dif8 und dif13. Man erkennt, dass die
Taylor-Reihe eine sehr viel genauere Methode zur Berechnung von „e“ liefert als
die Formel e = Grenzwert für N gegen unendlich von (1+1/N)^N