Differenzen- und Differentialgleichung Wachstumsprozesse Für die

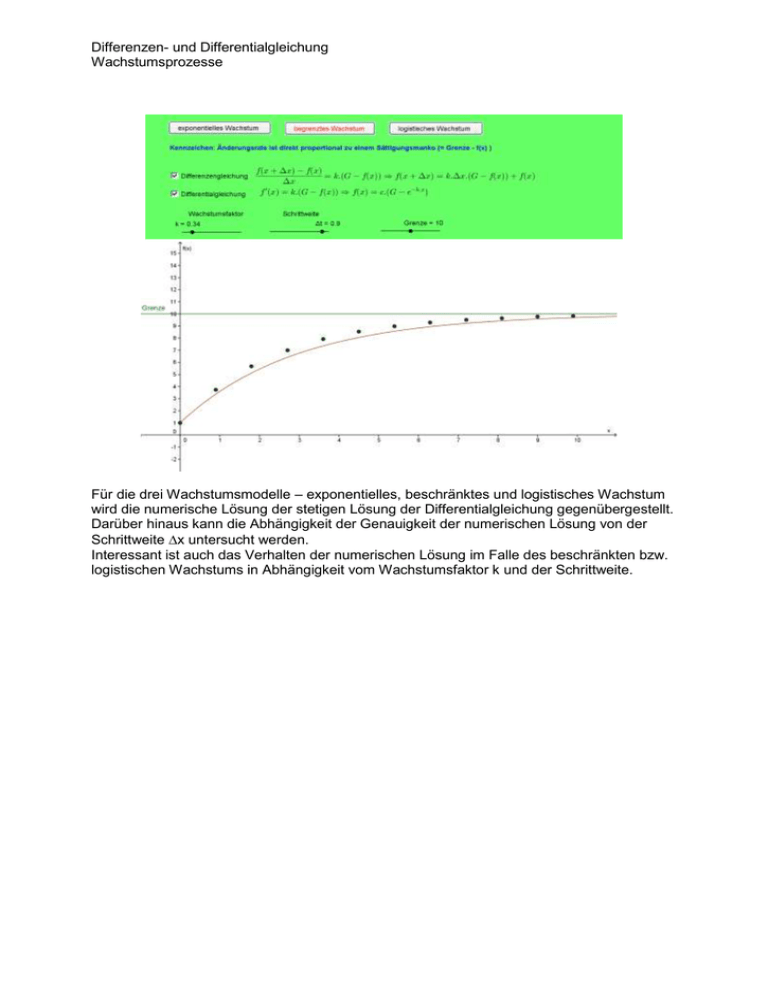
Differenzen- und Differentialgleichung
Wachstumsprozesse
Für die drei Wachstumsmodelle – exponentielles, beschränktes und logistisches Wachstum
wird die numerische Lösung der stetigen Lösung der Differentialgleichung gegenübergestellt.
Darüber hinaus kann die Abhängigkeit der Genauigkeit der numerischen Lösung von der
Schrittweite x untersucht werden.
Interessant ist auch das Verhalten der numerischen Lösung im Falle des beschränkten bzw.
logistischen Wachstums in Abhängigkeit vom Wachstumsfaktor k und der Schrittweite.
Numerisches Lösen der DGL 2. Ordnung a(t)=-².x (Schwingungsgleichung)
Das Euler’sche Streckenzugverfahren (oder kurz Euler-Verfahren) extrapoliert die gesuchte
Funktion x(t) mit Hilfe der durch v(t) gegebenen Steigung.
Als Anfangsbedingungen wählen wir x(0) = 1 und v(0)=0 sowie ²= 1.
Diese DGL 2. Ordnung lässt sich zerlegen in zwei DGLs 1. Ordnung
dx
dv
=
−ω²
x
und
v
=
dt
dt
Diese beiden Diff erentialgleichungen werden in Diff erenzengleichungen überführt, die direkt
in das numerische Schema eingebaut werden können:
∆v = −ω² x ∆t und ∆x = v∆t .
Dieses Schema lässt sich mit Hilfe der Tabellenkalkulation realisieren.
Zwei Fälle werden unterschieden: Einmal wird die Steigung zu Beginn des Intervalls [t, t+ t]
ermittelt, das andere Mal in der Mitte des Intervallls.
Die Abhängigkeit der numerischen Lösung von der Schrittweite t und von der Methode
kann mit diesem Applet untersucht werden.
Integralfunktion
siehe Applet