Kapitel 6 – Gewöhnliche Differenzialgleichungen (DGL)

Kapitel 6 – Gewöhnliche
Differenzialgleichungen (DGL)






Problemstellung
Beispiele
Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs
Einschrittverfahren
Stabilität & Schrittweitenkontrolle
Mehrschrittverfahren
Numerische Mathematik II
Herbsttrimester 2012
1
Problemstellung:
 Differenzialgleichungen tauchen in vielen technischen
mathematischen und naturwissenschaftlichen Vorgängen auf. Man
kann gewisse Eigenschaften einer Funktion mit Hilfe Ihrer
Ableitungen beschreiben kennt aber nicht den Verlauf der Funktion.
Die Aufgabe der Mathematik besteht nun darin die Funktion selbst
zu bestimmen.
 Eine geschlossene Lösungstheorie zur analytischen Lösung
allgemeiner DGL existiert nicht (Ausnahme z.B. lineare DGL mit
konstanten Koeffizienten). Man muss daher im Regelfall auf
numerische Verfahren zurückgreifen.
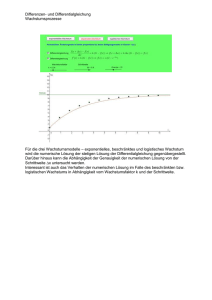
Bsp. 6.1 Wachstumsprozesse: Bezeichnen wir die Bevölkerungszahl
mit 𝑦 und die Wachstumsrate mit 𝑦′. Es ist leicht einzusehen dass die
Wachstumsrate proportional zur Bevölkerung ist: 𝑦 ′ (𝑡) = 𝑐𝑦(𝑡). Die
allgemeine Lösung lautet 𝑦 𝑡 = 𝑘 ⋅ 𝑒 𝑐𝑡 mit einer Konstanten 𝑘. Die
Lösung wird eindeutig wenn wir einen Anfangswert spezifizieren z.B.
𝑦 0 = 𝑦0 ⇒ 𝑘 = 𝑦0 . Man spricht dann von einem Anfangswertproblem.
Die obige DGL ist linear.
Numerische Mathematik II
Herbsttrimester 2012
2
Bsp. 6.2 In Beispiel 6.1 haben wir angenommen, dass die Bevölkerung
unendlich wachsen kann. Da der Lebensraum und offenbar die
Ressourcen beschränkt sind nehmen wir an die Population kann einen
Wert B nicht übersteigen. Man erhält dann die Modell-Gleichung:
𝑦 ′ 𝑡 = 𝑐𝑦 𝑡 1 − 𝑦/𝐵
Falls 𝑦 ≪ 𝐵 entspricht dies Bsp 6.1. Wenn 𝑦 = 𝐵 findet keine Wachstum mehr statt. Die DGL ist nicht linear - es tauchen Terme in 𝑦 2 auf.
Bsp. 6.3 Betrachten wir nun 2 wechselwirkende Populationen. Sei z.B.
𝑦1 die Anzahl der Füchse und 𝑦2 die Anzahl der Hasen. Nehmen wir an
Füchse ernähren sich ausschließlich von Hasen und Hasen haben als
natürliche Feinde nur Füchse. Das Nahrungsangebot für Hasen sei
unbegrenzt. Man erhält das vereinfachte Modell:
𝑦1′ 𝑡 = 𝐶1 𝑦1 𝑡 𝑦2 𝑡 − 𝐷1 𝑦1 𝑡
𝑦2′ 𝑡 = 𝐶2 𝑦2 𝑡 − 𝐷2 𝑦1 𝑡 𝑦2 𝑡
Dabei beschreibt 𝐶1 die Vermehrung der Füchse, 𝐷1 deren Sterberate,
𝐶2 das Wachstum der Hasenpopulation 𝐷2 deren Sterberate durch
Gefressenwerden. Wir erhalten ein System gekoppelter DGL.
Numerische Mathematik II
Herbsttrimester 2012
3
Bsp. 6.4 Das folgende System aus nichtlinearen Differenzialgleichungen beschreibt die Bewegung eines konventionellen Flächenflugzeuges
in der Symmetrieebene (Quelle: Wohler, Schulte).
Differenzialgleichungen:
Kräfte & Momente:
W
F
V    g sin   cos 
m
m
A
g
F
 
 cos  
sin 
mV V
mV
M
q 
Iy
  q  
A  CA
 (H )
H  V sin 
R  V cos 
C A  C A  0, 0  C A   C A
V 2S
2
 (H ) 2
W  CW
V S
2
 (H ) 2
M  Cm
V Sl
2
  (H ) 

F  F0 max 
 0 
Beiwerte & Flugzeugpolare:
CW  CW 0  kCA2
Cm  Cm  0, 0  Cm   Cm
 Cmq q
l
V
 Cm 
l
V
n
Atmosphäre (0-11km):

.
 ( H )   0 1 

Numerische Mathematik II

H 
T0 
H

g
1
R H
Herbsttrimester 2012
4
Bsp. 6.5 Ein harmonischer ungedämpfter Oszillator kann
beschrieben werden durch das Zusammenwirken von
Federrückstellkraft (Hook) und Trägheitskraft (Newton).
Es gilt also 𝑚 ⋅ 𝑥 ′′ = 𝑚 ⋅ 𝑎 = −𝑐𝑥 oder 𝑥 ′′ = −𝑐/𝑚 ⋅ 𝑥 .
Wir erhalten eine DGL zweiter Ordnung (wegen 𝑥 ′′ ).
Bsp 6.6 Inkompressible Strömungen werden beschrieben durch die
Navier-Stokes Gleichungen. Diese lassen sich i.A. nur numerisch
lösen. Es handelt sich um gekoppelte partielle DGL (d.h. Ableitungen
nach >1 Variablen). Man beachte die Einsteinsche Summenkonvention: bei doppelten Indizes wird über den Index von 1-3 summiert.
Massenbilanz:
ui
0
xi
Impulsbilanz:
ui ui u j
  ui u j  1 p






t
x j
x j  x j xi   xi
Numerische Mathematik II
DNS eines Freistrahls
Herbsttrimester 2012
5
Die nächsten Folien zeigen eine Vielzahl weiterer Beispiele aus der
Automobilindustrie für die numerische Lösung gewöhnlicher und
partieller Differentialgleichungen.
Bsp 6.7 Betrachtungen am Motorgesamtsystem bzw. Gesamtfahrzeug.
(Verbrauchs- und Performanceberechnung, Turboladerauswahl,
Motor-Leistungsberechung)
Numerische Mathematik II
Herbsttrimester 2012
6
Bsp 6.8 Numerische Strömungsmechanik in der Automobilindustrie
(In-Zylinder Strömung, Auslasskrümmer, Kühlkreislauf)
Numerische Mathematik II
Herbsttrimester 2012
7
Bsp 6.9 Thermomechanik und Dynamik und in der Automobilindustrie
(Blocktememperaturen, Bohrungsverzüge, Pleuelberechnung, NVH
(Noise, Vibration Harshness)
Numerische Mathematik II
Herbsttrimester 2012
8
Bsp. 6.10 Wir betrachten die DGL 𝑦 ′ 𝑡 = 1 + 𝑦 𝑡 2 mit Lösungsschar
𝑦 𝑡 = tan(𝑡 + 𝑐). Differenzialgleichungen lassen sich mit Hilfe des
Richtungsfeldes wie folgt veranschaulichen. Es gilt: 𝑦 ′ 𝑡 = 𝑓(𝑡, 𝑦(𝑡)).
Das heißt wenn die Lösung 𝑦 𝑡 durch den Punkt (𝑡, 𝑦) verläuft so muss
er dort die Steigung 𝑦 ′ 𝑡 = 𝑓(𝑡, 𝑦(𝑡)) haben. Die Lösungskurven der
DGL laufen tangential zum Richtungsfeld. Die Lösung wird eindeutig
durch fixieren eines Punktes. Beispielsweise muss im Punkt 0,0 die
Lösung Steigung 1 haben.
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-2
Numerische Mathematik II
-1.5
-1
Herbsttrimester 2012
-0.5
0
0.5
1
1.5
2
9
Klassifikation von Differenzialgleichungen
Def. 6.1
(1) Sei 𝑓: 𝑎, 𝑏 × ℝ𝑚 → ℝ𝑚 stetig. Dann nennt man 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡
eine gewöhnliche DGL erster Ordnung. (Bsp. 6.1)
(2) Unter einer Lösung versteht man eine differenzierbare Funktion
𝑦: 𝑎, 𝑏 → ℝ𝑚 die (1) erfüllt.
(3) Für 𝑚 > 1 spricht man von einem DGL System (Bsp. 6.3 & 6.4)
(4) Man spricht von einem Anfangswertproblem (AWP) wenn 𝑦 die
DGL löst und zusätzlich gilt 𝑦 𝑡0 = 𝑦0 gilt. (Bsp. 6.1)
(5) Wir bezeichnen weiterhin 𝑦 (𝑚) 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , 𝑦 ′ 𝑡 , … , 𝑦 𝑚−1 (𝑡)
mit 𝑦 𝑡0 = 𝑦0 , 𝑦 ′ 𝑡0 = 𝑦01 , … , 𝑦 (𝑚−1) 𝑡0 = 𝑦0𝑚−1 als AWP m.-ter
Ordnung. Hier treten Ableitungen bis zur Ordnung 𝑚 auf. (Bsp. 6.5)
(6) Die DGL heißt linear wenn gilt 𝑦 ′ 𝑡 = 𝐴 𝑡 ⋅ 𝑦 𝑡 + 𝑔 𝑡 mit
𝐴: 𝑎, 𝑏 → ℝ𝑚,𝑚 (Bsp. 6.1)
(7) Die DGL heißt autonom falls 𝑦 ′ 𝑡 = 𝑓 𝑦 𝑡 , wenn also 𝑓 nicht
explizit von 𝑡 abhängt.
Numerische Mathematik II
Herbsttrimester 2012
10
(7) Die Differentialgleichungen oben heißen explizit. Eine implizite DGL
erster Ordnung wäre beispielsweise: G 𝑡, 𝑦 𝑡 , 𝑦′(𝑡) = 0. Wenn
man diese nach 𝑦′(𝑡) auflösen kann wird sie explizit.
(8) Verallgemeinert man das Problem auf mehrere Veränderliche also
sucht man statt einer, z.B. zeitlich variablen Funktion, eine die
(auch) vom Ort abhängt und treten in der DGL partielle Ableitungen
auf spricht man von partiellen Differentialgleichung (Bsp. 6.6) im
Gegensatz zur gewöhnlichen DGL.
Bemerkung:
Es ist immer möglich eine DGL 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , mit 𝑦 𝑡0 = 𝑦0 ,
𝑓: 𝑎, 𝑏 × ℝ𝑚 → ℝ𝑚 in autonome Form zu bringen. Wir definieren
hierzu eine zusätzliche nullte Komponente z0 𝑡 = 𝑡. Offenbar gilt
𝑧0′ 𝑡 = 1. Man erhält dann wie folgt ein äquivalentes System in
autonomer Form mit 𝐹: 𝑎, 𝑏 × ℝ𝑚+1 → ℝ𝑚+1
𝑡0
𝑧0 ′
1
𝑓1 𝑧0 (𝑡), 𝑧1 , … , 𝑧𝑚
𝑦01
𝑦1′
′
𝑧 :=
=
:= 𝐹 𝑧 𝑡
𝑧 𝑡0 =
⋮
⋮
⋮
′
𝑓𝑚 𝑧0 (𝑡), 𝑧1 , … , 𝑧𝑚
𝑦0𝑚
𝑦𝑚
Numerische Mathematik II
Herbsttrimester 2012
11
Weiterhin ist es immer möglich ein AWP m-ter Ordnung
𝑦 (𝑚) 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , … , 𝑦 𝑚−1 (𝑡) ,
𝑦 𝑡0 = y0 ,… , 𝑦 (𝑚−1) 𝑡0 = 𝑦0𝑚−1
in ein DGL System erster Ordung zur überführen. Hierzu werden
Hilfsvariablen eingeführt: 𝑧1 = 𝑦, 𝑧2 = 𝑦 ′ , … , 𝑧𝑚 = 𝑦 (𝑚−1) . Differenzieren
′
′ = 𝑦 𝑚 = 𝑓 𝑡, 𝑧 𝑡 , … , 𝑧 (𝑡) oder
ergibt: 𝑧1′ = 𝑧2 , … , 𝑧𝑚−1
= 𝑧𝑚 , 𝑧𝑚
1
𝑚
′
𝑧2
𝑧1
⋮
𝑧′: = ⋮ =
: = 𝐹 𝑡, 𝑧 𝑡
′
𝑓 𝑡, 𝑧1 , … , 𝑧𝑚
𝑧𝑚
𝑦0
⋮
𝑧 𝑡0 =
𝑦0𝑚−1
Oftmals ist numerische Software (z.B. auch MATLAB) nur für Systeme
erster Ordnung geschrieben (die Umformung ist dann notwendig).
Wir können uns für theoretische Betrachtungen auf DGLs erster
Ordnung beschränken. Wenn notwendig können wir auch annehmen,
dass diese autonom sind.
Numerische Mathematik II
Herbsttrimester 2012
12
Wir befassen uns in diesem Kapitel ausschließlich mit Anfangswertproblemen gewöhnlicher DGL. Folgender Satz ist ein klassisches
Resultat der Analysis (Beweis mit Banachschem Fixpunktsatz):
Satz 6.2 (Picard Lindelöf):
Sei 𝑓: 𝑎, 𝑏 × ℝ𝑚 → ℝ𝑚 stetig in allen Argumenten und lipschitzstetig
im zweiten Vektorargument, d.h. mit einer Konstanten 𝐿 ≥ 0 gelte
𝑓 𝑡, 𝑦 − 𝑓 𝑡, 𝑧 ≤ 𝐿 ⋅ 𝑦 − 𝑧 ∀𝑡 ∈ 𝑎, 𝑏 , 𝑦, 𝑧 ∈ ℝ𝑚
dann besitzt das AWP eine eindeutige Lösung.
Bemerkungen:
 Für 𝑚 = 1 ersetze man die Norm durch den Betrag
 Wenn die Bedingungen aus Satz 6.2 nur lokal erfüllt sind gibt es
immerhin eine lokale Lösung (d.h. definiert in der Umgebung des
Startwertes)
 Ist 𝑓 stetig partiell differenzierbar im zweiten Vektorargument dann
genügt 𝑓 lokal einer Lipschitz Bedingung
 Betrachte 𝑦 ′ = 3𝑦 2/3 , 𝑦 0 = 0. Die Lipschitzbedingung ist in 0
verletzt. Die Lösung ist nicht eindeutig: 𝑦𝛼 𝑡 ≔ 𝑡 − 𝛼 3+ , 𝛼 > 0
Numerische Mathematik II
Herbsttrimester 2012
13
Einschrittverfahren:
Die Mehrzahl der numerischen Verfahren zur Lösung von AWPs
arbeitet mit Diskretisierungen. Dazu wird das Intervall [𝑎, 𝑏] zerlegt in
diskrete Werte 𝑡0 < 𝑡1 < 𝑡2 < ⋯ mit den Schrittweiten ℎ𝑘 ≔ 𝑡𝑘+1 − 𝑡𝑘 .
Dann wird entweder die Ableitung in
𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡
oder das Integral in der zum AWP (Def. 6.1) äquivalenten Formulierung
𝑡
𝑦 𝑡 = 𝑦0 +
𝑓 𝜏, 𝑦 𝜏 𝑑𝜏
(∗)
𝑡0
durch eine Näherung ersetzt. Wir bezeichnen die exakte Lösung an der
Stelle 𝑡𝑘 mit 𝑦 𝑡𝑘 = 𝑦𝑘 . Die diskret definierte Näherungslösung des
AWP bezeichnen wir im Folgenden mit 𝑢𝑘 ≈ 𝑦 𝑡𝑘 . Für die Ableitung
benutzen wir die äquivalenten Bezeichnungen: 𝑢𝑘′ = 𝑓𝑘 ≔ 𝑓(𝑡𝑘 , 𝑢𝑘 ).
Zur Illustration der Idee kehren wir zurück zu Beispiel 6.7.
Numerische Mathematik II
Herbsttrimester 2012
14
Bsp. 6.11 Das denkbar einfachste numerische Verfahren erhält man
indem man 𝑦′(𝑡𝑖 ) durch (𝑦 𝑡𝑖+1 − 𝑦 𝑡𝑖 )/ℎ𝑖 approximiert und in die
DGL einsetzt: 𝑢𝑛+1 ≔ 𝑢𝑛 + ℎ𝑛 𝑓𝑛 . Wir wollen eine Näherungslösung der
DGL 𝑦 ′ 𝑡 = 1 + 𝑦 𝑡 2 auf dem Intervall [0,1.2] berechnen mit 𝑦 0 = 0.
Als Schrittweite wählen wir ℎ = 0.2. Man erhält das Verfahren 𝑢0 = 0,
𝑢𝑛+1 ≔ 𝑢𝑛 + 0.2 ⋅ (1 + 𝑢𝑛2 ). Exakte Lösung und numerische Lösung
sind in der Abbildung unten gezeigt. Mit 𝑡𝑖 = 𝑖 ∗ 0.2, 𝑖 = 0, … , 6 erhält
man 𝑢𝑖 = [0 0.2000 0.4080 0.6413 0.9235 1.2941 1.8291]
2
1.5
1
0.5
0
-0.5
-1
-0.5
Numerische Mathematik II
0
0.5
1
Herbsttrimester 2012
1.5
2
15
Def. 6.3 Elementare Einschrittverfahren:
 das explizite Euler-Verfahren ist definiert durch die Vorschrift:
𝑢𝑛+1 ≔ 𝑢𝑛 + ℎ𝑛 𝑓𝑛 = 𝑢𝑛 + ℎ𝑛 𝑓(𝑡𝑛 , 𝑢𝑛 )
 das implizite Euler-Verfahren ist definiert durch
𝑢𝑛+1 ≔ 𝑢𝑛 + ℎ𝑛 𝑓𝑛+1 = 𝑢𝑛 + ℎ𝑛 𝑓 𝑡𝑛+1 , 𝑢𝑛+1
Bemerkung:
Man erhält das implizite Euler Verfahren indem man 𝑦′(𝑡𝑖+1 ) durch
(𝑦 𝑡𝑖+1 − 𝑦 𝑡𝑖 )/ℎ𝑖 approximiert (Rückwärtsdifferenz). In der Integralformulierung (∗) entspricht das der Approximation des Integrals durch
den Wert am rechten Rand multipliziert mit der Länge des Integrationsintervalls.
Das Verfahren heißt implizit weil 𝑢𝑛+1 auf beiden Seiten der Gleichung
auftaucht. Man muss bei der Berechnung i.A. eine nichtlineare
Gleichung lösen.
Numerische Mathematik II
Herbsttrimester 2012
16
Bevor wir weitere Verfahren definieren wollen wir uns mit Fragen der
Konvergenz beschäftigen. Betrachten wir den Fehler an der Stelle
𝑡 = 1 = 𝑡5 . Es gilt 𝑢5 = 𝑢4 + ℎ4 𝑓4 . Der Fehler an der Stelle 𝑡 = 1
(Differenz durchgezogene blaue (exakte Lsg DGL) und schwarze Linie
(Euler Verfahren)) setzt sich aus 2 Komponenten zusammen: Zum
einen dem Fehler der dadurch entsteht dass man bei 𝑡 = 0.8 von der
falschen Lösung losläuft, nämlich 𝑢4 statt 𝑦4 . Zum andernen dadurch,
dass man den Integranden im Integral ∗ durch eine Konstante ersetzt
also die Änderung der Steigung vernachlässigt. Die gestrichelte blaue
Linie zeigt die Exakte Lösung der DGL zum AW 𝑦 0.8 = 𝑢4 .
2
1.6
1.5
1.4
1
1.2
0.5
1
0
0.8
-0.5
0.6
-1
-0.5
0
Numerische Mathematik II
0.5
1
1.5
2
0.3
0.4
0.5
0.6
Herbsttrimester 2012
0.7
0.8
0.9
1
1.1
1.2
1.3
17
Wir benutzen im Folgenden die Tatsache, dass Einschrittverfahren
generell in der Form 𝑢𝑛+1 ≔ 𝑢𝑛 + ℎ𝑛 𝜙𝑓 (ℎ, 𝑡, 𝑢) geschrieben werden
können (vgl. z.B: Definition 6.3). Bei impliziten Verfahren steht
𝜙𝑓 (ℎ, 𝑡, 𝑢) allerdings für eine Vorschrift keine explizite Funktion.
Def. 6.4
 Globaler Fehler:
Sei 𝑒 ℎ, 𝑡 ≔ 𝑢𝑛 ℎ − 𝑦(𝑡) mit ℎ = (𝑡 − 𝑡0 )/𝑛 . Das Verfahren heißt
konvergent auf 𝑎, 𝑏 mit Ordnung 𝑝 falls 𝑒 ℎ, 𝑡 ≤ 𝐶 ℎ𝑝 .
 Lokaler Fehler:
Sei 𝑢𝑛 eine numerische Lsg. der DGL und 𝑧𝑛−1 die exakte Lsg. des
AWP 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , 𝑦 𝑡𝑛−1 = 𝑢𝑛−1 . Wir bezeichnen dann die
Größe 𝛿 ℎ, 𝑡, 𝑢 ≔ 𝑧𝑛−1 𝑡𝑛 − 𝑢𝑛 als lokalen Abbruchfehler.
 Der Konsistenzfehler ist definiert durch 𝜏 ℎ, 𝑡, 𝑢 ≔ 𝛿 ℎ, 𝑡, 𝑢 /ℎ.
 Ein Verfahren heiß konsistent wenn lim ‖𝜏 ℎ, 𝑡, 𝑢 ‖ = 0 gleichmäßig
ℎ→0
in 𝑡, 𝑢. Die Konsistenzordnung ist 𝑝, falls ‖𝜏 ℎ, 𝑡, 𝑢 ‖ ≤ 𝐶 ℎ𝑝 .
 Für Einschrittverfahren ist obige Defintion äquivalent zu
𝜏 ℎ, 𝑡, 𝑢 ≔ (𝑧𝑛−1 𝑡𝑛 − 𝑧𝑛−1 𝑡𝑛−1 )/ℎ𝑛−1 − 𝜙(ℎ, 𝑡, 𝑢)
Numerische Mathematik II
Herbsttrimester 2012
18
1.6
Globaler Fehler
Lokaler Fehler
1.4
1.2
Falscher Startwert
(globaler Fehler @ 𝑡 = 0.8)
1
0.8
Der lokale (Abbruch-)Fehler entspricht also dem in einem Zeitschritt
neu hinzukommenden Fehler.
Aus der Verfahrensdefinition 𝑢𝑛+1 ≔ 𝑢𝑛 + ℎ𝑛 𝜙𝑓 (ℎ, 𝑡, 𝑢) und der DGL
0.6
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
𝑓 𝑡𝑛 , 𝑦 𝑡𝑛 = 𝑦′ 𝑡𝑛 ≈ (𝑢𝑛+1 −𝑢𝑛 )/ℎ𝑛 = 𝜙𝑓 (ℎ, 𝑡, 𝑢) folgt durch
Grenzübergang ℎ → 0 die Notwendigkeit der Bedingung
lim 𝜙 ℎ, 𝑡, 𝑢 = 𝑓 𝑡, 𝑢 . Lemma 6.5 zeigt, dass diese notwendige
ℎ→0
Voraussetzung äquivalent ist zur Konsistenz des Verfahrens.
Später werden wir zeigen, dass für Einschrittverfahren (und nur für
diese) Konsistenz auch schon hinreichend ist für Konvergenz.
Numerische Mathematik II
Herbsttrimester 2012
19
Lemma 6.5
Die rechte Seite der DGL 𝑓(𝑡, 𝑦) sei stetig in 𝑡 und Lipschitz stetig in 𝑦.
Dann ist das Einschrittverfahren mit der Verfahrensfunktion 𝜙𝑓 genau
dann konsistent wenn gilt lim 𝜙 ℎ, 𝑡, 𝑢 = 𝑓 𝑡, 𝑢 gleichmäßig in 𝑡, 𝑢.
ℎ→0
Beweis: Sei 𝑧: = 𝑧𝑛−1 die Lsg. des AWP 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , 𝑦 𝑡𝑛−1 = 𝑢𝑛−1 .
Nach Definition 6.4 gilt für Einschrittverfahren:
𝜏 ℎ, 𝑡, 𝑢
= (𝑧 𝑡𝑛 − 𝑧 𝑡𝑛−1 )/ℎ − 𝜙 ℎ, 𝑡, 𝑢
=
(Mittelwertsatz, beachte dass θ nicht für jede Komponente identisch ist)
= 𝑧′ 𝑡 + θℎ − 𝜙 ℎ, 𝑡, 𝑢 = 𝑓 𝑡 + θℎ, 𝑧(𝑡 + θℎ) − 𝜙 ℎ, 𝑡, 𝑢 (∗)
Wenn also lim ‖𝜏 ℎ, 𝑡, 𝑢 ‖ = 0 so folgt lim 𝜙 ℎ, 𝑡, 𝑢 = 𝑓 𝑡, 𝑢 . Umgekehrt schätzt
ℎ→0
man 𝜏 ℎ, 𝑡, 𝑢
ℎ→0
durch (∗) nach oben ab durch 𝜏 ℎ, 𝑡, 𝑢
𝑓 𝑡 + θℎ, 𝑧(𝑡 + θℎ) − 𝜙 ℎ, 𝑡, 𝑢
≤
=
𝑓 𝑡 + 𝜃ℎ, 𝑧 𝑡 + 𝜃ℎ
− 𝑓 𝑡 + 𝜃ℎ, 𝑧 𝑡
+ 𝑓 𝑡 + 𝜃ℎ, 𝑧 𝑡 − 𝑓 𝑡, 𝑧 𝑡
+ 𝑓 𝑡, 𝑧 𝑡 − 𝜙 ℎ, 𝑡, 𝑢 (Teleskopsumme)
≤ 𝐿‖𝑧 𝑡 + θℎ − 𝑧 𝑡 ‖ + 𝑓 𝑡 + 𝜃ℎ, 𝑧 𝑡 − 𝑓 𝑡, 𝑧 𝑡
+ 𝑓 𝑡, 𝑧 𝑡 − 𝜙 ℎ, 𝑡, 𝑢
Die ersten beiden Summanden konvergieren für ℎ → 0 gegen 0. Damit folgt aus
lim 𝜙 ℎ, 𝑡, 𝑢 = 𝑓 𝑡, 𝑢 dass lim ‖𝜏 ℎ, 𝑡, 𝑢 ‖ = 0 und daher das Verfahren
ℎ→0
ℎ→0
konsistent ist.
Numerische Mathematik II
Herbsttrimester 2012
20
Bsp. 6.12 Sei 𝑧 Lösung des AWP 𝑧 ′ 𝑡 = 𝑓 𝑡, 𝑧 𝑡 , 𝑧 𝑡𝑛 = 𝑢𝑛
Es gilt nach Definition 6.4. 𝜏 ℎ, 𝑡, 𝑢 =
𝑧(𝑡𝑛+1 )−𝑧(𝑡𝑛 )
−
ℎ
𝜙 ℎ, 𝑡, 𝑢 (∗)
Wir entwickeln nun 𝑧 in eine Talyorreihe um 𝑡𝑛 . Es gilt also
ℎ2 ′′
𝑧
2
ℎ𝑧 ′
𝑧 𝑡𝑛+1 = 𝑧 𝑡𝑛 +
𝑡𝑛 +
𝑡𝑛 + ⋯ oder
𝑧 𝑡𝑛+1 − 𝑧 𝑡𝑛
ℎ ′′
ℎ2 ′′′
= 𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑧 𝑡𝑛 + 𝑧 𝑡𝑛 …
ℎ
2
6
Einsetzen in (∗) liefert für das explizite Euler Verfahren (𝜙 = 𝑓(𝑡𝑛 , 𝑢𝑛 )):
ℎ ′′
ℎ2 ′′′
𝜏 ℎ, 𝑡, 𝑢 = 𝑧 𝑡𝑛 + 𝑧 𝑡𝑛 + ⋯ = 𝑂(ℎ)
2
6
Das Euler Verfahren hat also Konsistenzordnung 1.
Offenbar erhält man eine Methode zur Herleitung eines Verfahrens der
Ordnung 𝑝 indem man setzt (beachte 𝑧 ′ 𝑡 = 𝑓 𝑡, 𝑧 𝑡 ):
𝑝
𝜙 ℎ, 𝑡, 𝑢 ≔
𝑘=1
ℎ𝑘−1
𝑧
𝑘!
𝑝
𝑘
𝑡 =
𝑘=1
ℎ𝑘−1 𝑑 𝑘−1
𝑓(𝑡, 𝑧(𝑡))
𝑘−1
𝑘! 𝑑𝑡
Das Problem dabei ist das aufwändige Ausrechnen der dabei
auftretenden partiellen Ableitungen mit Hilfe der Kettenregel.
Numerische Mathematik II
Herbsttrimester 2012
21
Da der globale Fehler sich zusammensetzt aus lokalem Abbruchfehler
und dem Fehler der dadurch entsteht, dass wir von einer falschen
Startlösung ausgehen, müssen wir uns damit befassen wie weit zwei
Lösungen der DGL zu unterschiedlichen Anfangswerten voneinander
abweichen können.
Satz 6.6
Seien ℎ und 𝑔 Lösungen der DGL 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 und die Funktion 𝑓
genüge einer Lipschitzbedingung in der zweiten Variablen. Dann gilt:
ℎ 𝑡 − 𝑔 𝑡 ≤ 𝑒 𝐿 𝑡−𝑡0 ⋅ ℎ 𝑡0 − 𝑔 𝑡0
Bemerkung: Aus Satz 6.6 folgt ebenfalls, dass die Lösung des AWPs
eindeutig sein muss.
Beweis: Mit Hilfe der Integralformulierung des AWP sieht man:
𝑡
𝑔 𝑡 − ℎ 𝑡 = 𝑔 𝑡0 − ℎ 𝑡0 +
Numerische Mathematik II
𝑓 𝜏, 𝑔 𝜏
− 𝑓 𝜏, ℎ 𝜏
𝑑𝜏 und daher
𝑡0
Herbsttrimester 2012
22
𝑡
𝑔 𝑡 −ℎ 𝑡
≤ 𝑔 𝑡0 − ℎ 𝑡0
Wir definieren 𝜙 𝑡 ≔
𝑡
𝑡0
+𝐿⋅
‖𝑔 𝜏 − ℎ 𝜏 ‖𝑑𝜏
𝑡0
𝑔 𝜏 − ℎ 𝜏 𝑑𝜏 ⇒ 𝜙 ′ (𝑡) = 𝑔 𝑡 − ℎ 𝑡
und
daher für t ≥ 𝑡0 𝛼 𝑡 ≔ 𝜙 ′ 𝑡 − 𝐿Φ 𝑡 ≤ 𝑔 𝑡0 − ℎ 𝑡0
(∗) .
Das AWP 𝜙 ′ 𝑡 = 𝛼 𝑡 + 𝐿Φ 𝑡 , 𝜙 𝑡0 = 0 hat für t ≥ 𝑡0 die Lösung
𝜙 𝑡 = 𝑒 𝐿(𝑡−𝑡0)
𝑡
𝛼 𝜏 𝑒 −𝐿(𝜏−𝑡0) 𝑑𝜏
(nachrechnen).
𝑡0
Es folgt mit (∗) die Abschätzung für t ≥ 𝑡0
0≤𝜙 𝑡 ≤
𝑒 𝐿 𝑡−𝑡0
𝑔 𝑡0 − ℎ 𝑡0
𝑡
𝑒 −𝐿
𝜏−𝑡0
𝑑𝜏
𝑡0
1
=
𝑔 𝑡0 − ℎ 𝑡0 𝑒 𝐿(𝑡−𝑡0) − 1
𝐿
Schließlich erhält man für die Behauptung für t ≥ 𝑡0
‖ℎ 𝑡 − 𝑔 𝑡 ‖ = 𝜙 ′ 𝑡 = 𝛼 𝑡 + 𝐿Φ 𝑡 ≤
1
≤ 𝑔 𝑡0 − ℎ 𝑡0 + L 𝑔 𝑡0 − ℎ 𝑡0 𝑒 𝐿 𝑡−𝑡0 − 1
𝐿
= 𝑔 𝑡0 − ℎ 𝑡0 𝑒 𝐿 𝑡−𝑡0 Für t < 𝑡0 geht man analog vor.
Numerische Mathematik II
Herbsttrimester 2012
23
Satz 6.7 Konvergenz von Einschrittverfahren
Sei 𝑦 die exakte Lösung des AWP 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 , 𝑦 𝑡0 = 𝑦0 und sei
𝑢𝑖 die von einem Einschrittverfahren erzeugte Näherungslösung gemäß
𝑢0 ≔ 𝑦0 , 𝑢𝑘 ≔ 𝑢𝑘−1 + ℎ𝑘−1 𝜙(ℎ𝑘−1 , 𝑡𝑘−1 , 𝑢𝑘−1 ). Die rechte Seite der
Gleichung sei Lipschitz stetig im zweiten Argument und das Verfahren
sei konsistent ‖𝜏 ℎ, 𝑡, 𝑢 ‖ ≤ 𝐶 ℎ𝑝 .
Dann gilt:
𝐿 𝑡𝑛 −𝑡0 − 1
𝑒
𝑦 𝑡𝑛 − 𝑢𝑛 ≤ C max ℎ𝑘 𝑝 ⋅
𝑘
𝐿
Beweis: Es bezeichne im Folgenden 𝑧𝑘 die exakte Lösung der DGL
zum Anfangswert (𝑡𝑘 , 𝑢𝑘 ) für alle 𝑘. Dann gilt nach Definition des
𝑧
(𝑡 )−𝑢
𝑧
(𝑡 )−𝑧 (𝑡 )
Konsistenzfehlers: 𝜏 ℎ𝑘−1 , 𝑡𝑘−1 , 𝑢𝑘−1 = 𝑘−1 𝑘 𝑘 = 𝑘−1 𝑘 𝑘 𝑘
ℎ𝑘−1
Nach Voraussetzung gilt daher ‖𝑧𝑘−1 (𝑡𝑘 ) − 𝑧𝑘 (𝑡𝑘 )‖ ≤
ℎ𝑘−1
𝑝+1
𝐶ℎ𝑘−1
Mit Satz 6.6 sieht man (beachte 𝑧𝑘−1 Lösung des AWP zum Anfangswert (𝑡𝑘−1 , 𝑢𝑘−1 ) aber auch zum Anfangswert (𝑡𝑘 , 𝑧𝑘−1 (𝑡𝑘 )) )
‖𝑧𝑘−1 (𝑡𝑛 ) − 𝑧𝑘 (𝑡𝑛 )‖ ≤ ‖𝑧𝑘−1 (𝑡𝑘 ) − 𝑧𝑘 (𝑡𝑘 )‖ 𝑒 𝐿 𝑡𝑛 −𝑡𝑘
Numerische Mathematik II
Herbsttrimester 2012
24
Wir betrachten wieder eine Teleskopsumme
𝑛
𝑢𝑛 − 𝑦 𝑡𝑛 = 𝑧𝑛 (𝑡𝑛 ) − 𝑧0 𝑡𝑛 =
𝑘=1
𝑛
𝑢𝑛 − 𝑦 𝑡𝑛
≤
𝑧𝑘 𝑡𝑘 − 𝑧𝑘−1 𝑡𝑘
𝑘=1
≤
𝑝
𝐶 max{ℎ𝑘−1 }
𝑘
𝑧𝑘 𝑡𝑛 − 𝑧𝑘−1 𝑡𝑛
⇒
𝑛
𝑝+1
𝑒 𝐿 𝑡𝑛−𝑡𝑘 ≤
𝐶ℎ𝑘−1 𝑒 𝐿 𝑡𝑛−𝑡𝑘 ≤
𝑘=1
𝑛
𝑒 𝐿 𝑡𝑛 −𝑡𝑘 ℎ𝑘−1 ≤ 𝐶 max ℎ𝑘−1
𝑘
𝑘=1
𝑝
𝑡𝑛
𝑒 𝐿 𝑡𝑛 −𝑡 𝑑𝑡
𝑡0
Bemerkungen:
 Für Einschrittverfahren folgt aus Konsistenz bereits Konvergenz. Die
Konsistenzordnung entspricht der Konvergenzordnung (entspricht
der Ordnung des lokalen Abbruchfehler -1)
 Wir haben beim Beweis die Abschätzung benutzt wie weit zwei
Lösungen zu unterschiedlichen Startwerten voneinander abweichen
können und den lokalen Abbruchfehler.
 Die Bedeutung des Satzes liegt darin, dass man Konsistenz sehr
viel leichter überprüfen kann, z.B. mit der Taylorreihe.
Numerische Mathematik II
Herbsttrimester 2012
25
Wir wollen nun weitere Verfahren kennenlernen. Hilfreich ist hier die
Integralformulierung des AWP. Wir können nun verschiedene
numerische Integrationsformeln zur Bestimmung der Verfahrensfunktion anwenden.
𝑦(𝑡𝑛+1 ) = 𝑦(𝑡𝑛 ) +
𝑡𝑛+1
𝑓 𝜏, 𝑦 𝜏 𝑑𝜏
𝑡𝑛
Taucht bei der Integration ein Wert 𝑦 𝑡 auf den man noch nicht
bestimmt hat gibt es zwei Möglichkeiten:
(1) man lässt den unbekannten Wert auf der rechten Seite stehen und
erhält dann ein implizites Verfahren. Beim impliziten Euler
𝑡
Verfahren setzt man z.B. 𝑡 𝑛+1 𝑓 𝜏, 𝑦 𝜏 𝑑𝜏 ≈ ℎ𝑛 𝑓(𝑡𝑛 , 𝑦 𝑡𝑛+1 )
𝑛
(2) Die zweite Methode besteht darin einen Schätzwert für das
unbekannte 𝑓 𝑡, 𝑦 𝑡 zu ermitteln. Hierbei kommt dann ein
explizites Verfahren, häufig das Euler Verfahren, zum Einsatz.
Numerische Mathematik II
Herbsttrimester 2012
26
Zunächst eine kurze Wiederholung aus der Analysis:
 Taylorreihe einer reell-wertigen Funktion von 2 Veränderlichen:
𝜕
𝜕
𝑓 𝑥1 + ℎ1 , 𝑥2 + ℎ2 = 𝑓 𝑥1 , 𝑥2 + ℎ1
𝑓 𝑥1 , 𝑥2 + ℎ2
𝑓 𝑥1 , 𝑥2 +
𝜕𝑥1
𝜕𝑥2
2
2
𝜕
𝜕
𝜕 𝜕
2
2
ℎ1 2 𝑓 𝑥1 , 𝑥2 + ℎ2 2 𝑓 𝑥1 , 𝑥2 + ℎ1 ℎ2
𝑓 𝑥1 , 𝑥2 + ⋯
𝜕𝑥1 𝜕𝑥2
𝜕𝑥1
𝜕𝑥2
 Kettenregel für Funktionen mit einem Parameter
d
𝜕
𝜕𝑥1
𝜕
𝜕𝑥2
𝑓 𝑥1 (𝑡), 𝑥2 (𝑡) =
𝑓 𝑥1 , 𝑥2 ⋅
+
𝑓 𝑥1 , 𝑥2 ⋅
dt
𝜕𝑥1
𝜕𝑡 𝜕𝑥2
𝜕𝑡
Numerische Mathematik II
Herbsttrimester 2012
27
Satz 6.8
Beide Euler-Verfahren haben Konsistenzordnung 𝑝 = 1. Alle folgenden
Verfahren haben Konsistenzordnung 𝑝 = 2.
 Die Mittelpunktsregel. Sie kann auch als 2-stufiges Runge-Kutta
Verfahren angesehen werden.
ℎ
𝑢𝑛+1/2 = 𝑢𝑛 + 𝑓 𝑡𝑛 𝑢𝑛 ,
𝑢𝑛+1 = 𝑢𝑛 + ℎ𝑓(𝑡𝑛+1/2 , 𝑢𝑛+1/2 )
2
Man schreibt auch:
𝑘1 = 𝑓 𝑡𝑛 , 𝑢𝑛 , 𝑘2 = 𝑓 𝑡𝑛 + ℎ/2, 𝑢𝑛 + ℎ/2 𝑘1 , 𝑢𝑛+1 = 𝑢𝑛 + ℎ𝑘2
 Das Heun-Verfahren entsteht aus der Trapezregel durch Schätzen
von 𝑦𝑛+1 mit einem Eulerschritt
ℎ
𝑘1 = 𝑓 𝑡𝑛 , 𝑢𝑛 , 𝑘2 = 𝑓 𝑡𝑛 + ℎ, 𝑢𝑛 + ℎ𝑘1 , 𝑢𝑛+1 = 𝑢𝑛 + (𝑘1 + 𝑘2 )
2
Man nennt es auch Prädiktor-Korrektor weil man 𝑢𝑛+1 erst
vorhersagt und dann korrigiert.
 Das Crank-Nicolson Verfahren entsteht ebenfalls aus der
Trapezregel ist aber implizit:
ℎ
𝑢𝑛+1 = 𝑢𝑛 + 𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛+1 , 𝑢𝑛+1
2
Numerische Mathematik II
Herbsttrimester 2012
28
Beweis: Es gilt 𝜏 ℎ, 𝑡, 𝑢 =
𝑧(𝑡𝑛+1 )−𝑧(𝑡𝑛 )
−
ℎ
𝜙 ℎ, 𝑡, 𝑢 , 𝑧 𝑡𝑛 = 𝑢𝑛 .
Der Argumentation von Bsp. 6.12 folgend reicht es zu zeigen:
𝑝
ℎ𝑘−1 𝑑 𝑘−1
𝑝
𝜙 ℎ, 𝑡, 𝑢 =
𝑓
𝑡,
𝑧
𝑡
+
𝑂
ℎ
𝑘! 𝑑𝑡𝑘−1
𝑘=1
Das Euler-Verfahren wurde bereits behandelt. Betrachten wir die Verfahren zweiter Ordnung. Die obige Summe lautet dann (Kettenregel):
𝜙 = 𝑓 𝑡𝑛 , 𝑧 𝑡𝑛
+
ℎ
2
𝑓𝑡 𝑡𝑛 , 𝑧 𝑡𝑛
+
ℎ
2
𝑓𝑦 𝑡𝑛 , 𝑧 𝑡𝑛
⋅ 𝑓 𝑡𝑛 , 𝑧 𝑡𝑛
(∗)
Die Mittelpunktsregel hat die Verfahrensfunktion (Taylor)
𝜙 ℎ, 𝑡𝑛 , 𝑢𝑛 = 𝑓 𝑡𝑛 + ℎ/2, 𝑢𝑛 + ℎ/2𝑓 𝑡𝑛 , 𝑢𝑛 =
ℎ
ℎ
𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓𝑡 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛 , 𝑢𝑛 𝑓𝑦 𝑡𝑛 , 𝑢𝑛 + 𝑂 ℎ2
2
2
Beim Heun-Verfahren lautet die Verfahrensfunktion
1
𝜙 ℎ, 𝑡𝑛 , 𝑢𝑛 = 𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛 + ℎ, 𝑢𝑛 + ℎ𝑓 𝑡𝑛 , 𝑢𝑛
=
2
1
𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛 , 𝑢𝑛 + ℎ𝑓𝑡 𝑡𝑛 , 𝑢𝑛 + ℎ𝑓 𝑡𝑛 , 𝑢𝑛 𝑓𝑦 (𝑡𝑛 , 𝑢𝑛 ) + 𝑂 ℎ2
2
In beiden Fällen hat man also Übereinstimmung mit (∗) bis auf 𝑂 ℎ2 .
Numerische Mathematik II
Herbsttrimester 2012
29
Für das Crank Nicolson-Verfahren mit Verfahrensfunktion
1
𝜙 ℎ, 𝑡𝑛 , 𝑢𝑛 = 𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛+1 , 𝑢𝑛+1
2
betrachten wir wieder die Integralformulierung:
𝑧 𝑡𝑛+1 = 𝑧 𝑡𝑛 +
= 𝑧 𝑡𝑛
𝑡𝑛+1
𝑓
𝑡𝑛
𝜏, 𝑧 𝜏 𝑑𝜏 =
ℎ
+ 𝑓 𝑡𝑛 , 𝑢𝑛 + 𝑓 𝑡𝑛+1 , 𝑢𝑛+1
2
Es folgt 𝜏 ℎ, 𝑡, 𝑢 =
𝑧(𝑡𝑛+1 )−𝑧(𝑡𝑛 )
−
ℎ
(Corollar 3.12)
1 𝑑2
3
−
𝑓
𝜉,
𝑧
𝜉
ℎ
12 𝑑𝑡 2
𝜙 ℎ, 𝑡, 𝑢 = O(h2 ).
Wir wollen als nächstes Einschrittverfahren höherer Ordnung
definieren. Durch Abgleich der Koeffizienten mit
𝑝
ℎ𝑘−1 𝑑 𝑘−1
𝑝
𝑓
𝑡,
𝑧
𝑡
+
𝑂
ℎ
𝑘! 𝑑𝑡𝑘−1
𝑘=1
kann dabei die gewünschte Konsistenzordnung erreicht werden.
Numerische Mathematik II
Herbsttrimester 2012
30
Def. 6.9 Ein Einschrittverfahren der Form
𝑘𝑖 = 𝑓 𝑡𝑛 + 𝛼𝑖 ℎ, 𝑢𝑛 + ℎ
𝑢𝑛+1 = 𝑢𝑛 + ℎ ⋅
𝑖−1
𝑗=1 𝛽𝑖,𝑗 𝑘𝑗
für 𝑖 = 1, … , 𝑟
𝑟
𝑗=1 𝛾𝑗 𝑘𝑗
(1)
(2)
heißt r-stufiges explizites Runge-Kutta Verfahren.
Das RK-Verfahren ist genau dann konsistent wenn gilt
𝑟
𝑗=1 𝛾𝑗
=1
Beweis: Für ℎ = 0 gilt 𝑘𝑖 = 𝑓 𝑡𝑛 , 𝑢𝑛 . Die Behauptung folgt aus Lemma
6.5 mit Φ 𝑡, ℎ, 𝑢 = 𝑟𝑗=1 𝛾𝑗 𝑘𝑗 = 𝑓 𝑡𝑛 , 𝑢𝑛 .
Bemerkungen:
 Die Werte 𝑘𝑖 sind Funktionsauswertungen von 𝑓(𝑡, 𝑦(𝑡)) zu
definierten Zwischenschritten. Manchmal fordert man hier auch noch
die sog. Zeilensummenbedingung: 𝛼𝑖 = 𝑖−1
𝑗=1 𝛽𝑖,𝑗
 Formel (2) kann als Quadraturformel interpretiert werden.
 Da in (1) die Summe bis 𝑖 − 1 läuft handelt es sich hier um explizite
Verfahren. Man kann analog auch implizite RK-Verfahren definieren.
 Alle bisher betrachteten Verfahren können in obige Form gebracht
werden und somit als Runge-Kutta Verfahren angesehen werden.
Numerische Mathematik II
Herbsttrimester 2012
31
Satz 6.10 (Butcher-Schranken)
Ein r-stufiges explizites Runge-Kutta Verfahren kann bestenfalls
Konsistenzordnung 𝑝 = 𝑟 erreichen falls 𝑟 ≤ 4. Für 𝑟 = 5,6,7 gilt
𝑝 ≤ 𝑟 − 1, für 𝑟 = 8,9 gilt 𝑝 ≤ 𝑟 − 2 für 𝑟 ≥ 10 gilt 𝑝 ≤ 𝑟 − 3.
Bemerkungen:
 In obigem Sinn sind also RK-4 Verfahren optimal.
 Man kann Runge-Kutta Verfahren unterschiedlicher Konsistenzordnung kombinieren um den Fehler zu schätzen und damit die Schrittweite zu kontrollieren (vergleiche adaptive numerische Integration).
Ein berühmter Vertreter dieser Gattung ist das 6-stufige Fehlberg
Verfahren. Dort kann man die 𝑘𝑖 auf unterschiedliche Weisen so
kombinieren, dass ein Verfahren 4. bzw. 5. Ordnung entsteht.
 Speziell entwickelt für die Anwendung bei partiellen DGLs gibt es
auch sogenannte low-storage RK Verfahren, bei denen man die
gesuchte Lösungsvariable weniger als 𝑟 mal speichern muss.
 Implizite Runge Kutta Verfahren können maximal die
Konsistenzordung 𝑝 = 2𝑟 erreichen.
Numerische Mathematik II
Herbsttrimester 2012
32
Def. 6.11 Das bekannteste klassische explizite Runge-Kutta Verfahren
vierter Ordnung lautet:
𝑘1 = 𝑓(𝑡𝑛 , 𝑢𝑛 )
𝑘2 = 𝑓 𝑡𝑛 + ℎ/2, 𝑢𝑛 + ℎ/2 ⋅ 𝑘1
𝑘3 = 𝑓 𝑡𝑛 + ℎ/2, 𝑢𝑛 + ℎ/2 ⋅ 𝑘2
𝑘4 = 𝑓 𝑡𝑛 + ℎ, 𝑢𝑛 + ℎ ⋅ 𝑘3
ℎ
𝑢𝑛+1 = 𝑢𝑛 + 𝑘1 + 2𝑘2 + 2𝑘3 + 𝑘4
6
Es hat Konsistenzordnung 4.
Das folgende Zitat aus Referenz [2] beschreibt sehr treffend die
Eigenschaften des obigen Verfahrens.
“For many scientific users, fourth-order Runge-Kutta is not just the first
word on ODE integration, but the last word as well. In fact, you can get
pretty far on this old workhorse, especially if you combine it with an
adaptive stepsize algorithm”.
Numerische Mathematik II
Herbsttrimester 2012
33
Wir haben bereits festgestellt, dass bei impliziten Verfahrensfunktionen
i.A. eine nichtlineare Gleichung zu lösen ist. Hierzu kann man auf die
bekannten Verfahren der Numerik I zurückgreifen. Speziell kann man
für ein implizites Verfahren 𝜙2 von Ordnung 𝑝 die Fixpunktiteration
(𝑘+1)
𝑢𝑛+1 = 𝑢𝑛 + ℎ𝜙2 ℎ, 𝑡𝑛+1 , 𝑢𝑛+1 (𝑘) (Korrektor)
anwenden wobei der Anfangswert
(0)
𝑢𝑛+1 = 𝑢𝑛 + ℎ𝜙1 ℎ, 𝑡𝑛 , 𝑢𝑛 (Prädiktor)
mit einem beliebigen expliziten Verfahren berechnet werden kann,
welches mindestens die Ordnung 𝑝 − 1 haben sollte. Das Prädiktor
Korrektor Verfahren konvergiert, wenn 𝜙2 Lipschitz stetig in 𝑢𝑘 ist, denn
dann gilt für die Iterationsfunktion 𝜓 𝑥 ≔ 𝑢𝑛 + ℎ𝜙2 … , 𝑥
‖ 𝜓 𝑥 − 𝜓 𝑦 = h 𝜙2 ℎ, 𝑡𝑛+1 , 𝑥 − 𝜙2 ℎ, 𝑡𝑛+1 , 𝑦 ≤ ℎ𝐿 𝑥 − 𝑦‖.
Mit anderen Worten die Abbildung ist für ausreichend kleines ℎ
kontrahierend ( Zeitschrittbedingung). In der Praxis bricht man
meistens nach wenigen Iterationen ab (z.B. einer oder zwei). Formal
erhält man dann wieder ein explizites Verfahren. Man vergleiche das
obige Vorgehen mit dem Heun Verfahren.
Numerische Mathematik II
Herbsttrimester 2012
34
Bsp. 6.13 Die Abbildungen unten zeigen die numerische Lösung
unseres AWP aus Beispiel 6.10 𝑦 ′ 𝑡 = 1 + 𝑦 𝑡 2 , 𝑦 0 = 0 auf dem
Intervall 0,1 mit ℎ = 0.2 für das explizite Euler Verfahren, das CrankNicolson Verfahren und Runge Kutta Verfahren 4. Ordnung. Das
Runge Kutta Verfahren stimmt an den berechneten Stellen bereits fast
perfekt mit der exakten Lösung überein.
1.8
1.8
Exakte Lsg.
Euler explizit
Crank Nicolson
Runge Kutta 4. Ord.
1.6
1.4
1.6
Exakte Lsg.
Euler explizit
Crank Nicolson
Runge Kutta 4. Ord.
1.4
1.2
1
y(t)
y(t)
1.2
0.8
1
0.6
0.8
0.4
0.6
0.2
0
0
0.1
0.2
Numerische Mathematik II
0.3
0.4
0.5
t
0.6
0.7
0.8
0.9
1
0.4
0.5
Herbsttrimester 2012
0.55
0.6
0.65
0.7
0.75
t
0.8
0.85
0.9
0.95
1
35
Stabilität & Schrittweitenkontrolle
 Die Stabilität von numerischen Verfahren spielt eine herausragende
Rolle für deren Anwendbarkeit in der Praxis. Der Begriff Stabilität ist
dabei nicht einheitlich definiert. Wir unterscheiden im Folgenden
zwei Definitionen:
 Nullstabilität:
Die Nullstabilität bezieht sich auf das Verhalten des Verfahrens im
Grenzfall ℎ → 0. Das Integrationsintervall 0, 𝑇 wird dabei
festgehalten. Sie sichert eine schwache Sensitivität des Verfahrens
gegenüber kleinen Änderungen in den Daten (z.B. Rundungsfehler).
Nullstabilität ist also wichtig bei der Konstruktion von Verfahren.
 Absolute Stabilität:
Die absolute Stabilität eines numerischen Verfahrens zur Lösung
einer DGL bezieht sich auf die Beschränktheit der Lösung bei
festem ℎ und wachsendem Integrationsintervall 0, 𝑇 , 𝑇 → ∞. Die
absolute Stabilität ist wichtig bei der Anwendung von Verfahren, da
sich hieraus ein Kriterium an den Zeitschritt ableiten lässt.
Numerische Mathematik II
Herbsttrimester 2012
36
Def. 6.12 Das numerische Verfahren zur Lösung des AWP mittels
einem Einschrittverfahren heißt nullstabil, wenn für alle Störungen mit
𝛿𝑘 ≤ 𝜀 gilt:
ℎ
ℎ
∃ℎ0 > 0, ∃𝐶 > 0: ∀ℎ ∈ 0, ℎ0 𝑧𝑛 − 𝑢𝑛 ≤ 𝐶𝜀 ∀0 ≤ 𝑛 ≤ 𝑁ℎ
wobei 𝑧𝑛 , 𝑢𝑛 die Lösungen der Probleme
𝑧𝑛+1 = 𝑧𝑛 + ℎ 𝜙 ℎ, 𝑡𝑛 , 𝑧𝑛 + 𝛿𝑛+1 ,
𝑢𝑛+1 = 𝑢𝑛 + ℎ 𝜙 ℎ, 𝑡𝑛 , 𝑢𝑛 ,
Darstellen.
𝑧0 = 𝑦0 + 𝛿0
𝑢0 = 𝑦0
Bemerkungen:
 Man kann zeigen, dass Einschrittverfahren auf Grund der
Lipschitzstätigkeit nullstabil sind. Konsistenz ist bei
Einschrittverfahren hinreichend für die Konvergenz (Satz 6.7)
 Für Mehrschrittverfahren gilt dies i.A. nicht. Ein konsistentes
Mehrschrittverfahren ist genau dann konvergent wenn es nullstabil
ist (siehe Äquivalenzsatz von Lax-Richtmyer & Satz 6.17).
Numerische Mathematik II
Herbsttrimester 2012
37
Zur Untersuchung der absoluten Stabilität betrachten wir ein spezielles
Testproblem: 𝑦 ′ 𝑡 = 𝜆𝑦 𝑡 , 𝑦 0 = 1 mit Re 𝜆 < 0 (∗)
Man beachte, dass in diesem Fall lim 𝑦 𝑡 = 0 gilt. Man stellt nun die
𝑡→∞
Mindestanforderung, dass das numerische Verfahren das
asymptotische Verhalten korrekt wiedergibt:
Def. 6.13 Ein numerisches Verfahren zur Approximation von (∗) heißt
absolut stabil wenn gilt: 𝑢𝑛 → 0 für 𝑛 → ∞ .
Die numerische Lösung von (∗) hängt von ℎ, 𝜆 ab. Wir bezeichnen mit
𝐴 ≔ 𝑧 ≔ ℎ𝜆 ∈ ℂ | 𝑢𝑛 → 0 für 𝑛 → ∞
den Bereich der absoluten Stabilität des Verfahrens.
Ein Verfahren heißt A-stabil wenn 𝑧 ∈ ℂ | 𝑅𝑒 𝑧 < 0 ⊂ 𝐴, d.h. das
Verfahren liefert das richtige asymptotische Verhalten für alle ℎ > 0.
Bemerkung:
Man fordert natürlich nicht, dass für jede DGL die asymptotische
Lösung gegen Null strebt. Man beobachtet aber, dass für DGL deren
exakte Lösung nicht gegen Null strebt die Eigenschaft der absoluten
Stabilität kleine Störungen kontrolliert, also auch vorteilhaft ist.
Numerische Mathematik II
Herbsttrimester 2012
38
Bsp. 6.14 Absolute Stabilität der Euler-Verfahren:
Wir wollen die DGL 𝑦 ′ 𝑡 = 𝜆𝑦 𝑡 , 𝑦 0 = 1 mit Re(𝜆) < 0 mit den
Euler Verfahren lösen (beachte 𝜆 ≔ 𝑎 + 𝑖𝑏 ⇒ 𝑒 𝑎+𝑖𝑏 𝑡 =
𝑒 𝑎𝑡 [cos 𝑏𝑡 + 𝑖 sin 𝑏𝑡 ]). Man erhält für die explizite Methode:
𝑢0 = 1, 𝑢𝑛+1 = 𝑢𝑛 + ℎ𝜆𝑢𝑛 = 𝑢𝑛 1 + ℎ𝜆 = 𝑢0 1 + ℎ𝜆 𝑛+1
Für absolute Stabilität muss gelten: 1 + ℎ𝜆 < 1 Wenn ℎ positiv und 𝜆
reell ist, ist dies äquivalent zu ℎ < 2/|𝜆|.
Das implizite Euler Verfahren ergibt:
𝑢0 = 1, 𝑢𝑛+1 = 𝑢𝑛 + ℎ𝜆𝑢𝑛+1 und daher 𝑢𝑛+1 =
𝑢𝑛
1−ℎ𝜆
=
𝑛+1
1
1−ℎ𝜆
Absolute Stabilität erhält man also für den Bereich 1 − ℎ𝜆 > 1.
Wenn ℎ positiv und 𝜆 reell ist, ist dies äquivalent zu ℎ > 0 beliebig.
Im(ℎ𝜆)
Die Abbildungen zeigen die
Bereiche absoluter Stabilität für das explizite (links)
und das implizite Euler
Verfahren (rechts).
Numerische Mathematik II
−1
1 Re(ℎ𝜆)
Herbsttrimester 2012
Im(ℎ𝜆)
−1
1 Re(ℎ𝜆)
39
Bsp 6.15
Wir berechnen mit den Euler Verfahren die Lösung des AWP
𝑦 ′ 𝑡 = −1 ⋅ 𝑦 𝑡 , 𝑦 0 = 1 . Für das explizite Verfahren muss gelten:
ℎ < 2. Die Abbildungen zeigen das Verhalten des expliziten (links) und
impliziten (rechts) Verfahrens für verschiedene Schrittweiten.
4
4
h=2.1
h=1.9
h=2/3
exp(-t)
3
2
2
1
1
0
0
-1
-1
-2
-2
-3
-3
-4
0
5
Numerische Mathematik II
2/3
2.1
h=6
exp(-t)
3
10
15
20
25
30
-4
0
Herbsttrimester 2012
5
10
15
20
25
30
40
Bsp. 6.16 Das Crank-Nicolson und beispielhaft 3 explizite Runge-Kutta
Verfahren haben die folgenden Stabilitätsbereiche (siehe auch Übung):
 Crank Nicolson Verfahren: 𝐴 = 𝑧 ∈ ℂ ∶ Re(𝑧) ≤ 0
 Euler-Verfahren: 𝐴 = 𝑧 ∈ ℂ ∶ 1 + 𝑧 ≤ 1
 Mittelpunktsregel: 𝐴 = 𝑧 ∈ ℂ ∶ 1 + 𝑧 +
𝑧2
2
≤1
 Klassisches RK4: 𝐴 = 𝑧 ∈ ℂ ∶ 1 + 𝑧 +
𝑧2
2
𝑧3
6
+
+
𝑧4
24
≤1
Der Stabilitätsbereich der Crank-Nicolson Methode ist links zu sehen.
Bei expliziten RK Verfahren nimmt die Größe des Bereichs mit der
Ordnung zu. Er entspricht dem inneren der gekennzeichneten Flächen
in der Abbildung rechts.
Im(ℎ𝜆)
4
Euler explizit
Heun
Runge Kutta 4
3
Im(ℎ𝜆)
2
y
1
−1
1 Re(ℎ𝜆)
0
1
−1
Re(ℎ𝜆)
-1
-2
-3
Numerische Mathematik II
Herbsttrimester 2012
-4
-4
-3
-2
-1
x
0
1
2
41
Bemerkung:
Wir haben bisher nur die Stabilität skalarer DGL betrachtet. Wir wollen
uns nun der Frage zuwenden wie wir den Stabilitätsbegriff auf DGLSysteme verallgemeinern können und welche Schwierigkeiten dabei
auftreten können.
Betrachten wir zunächst ein lineares System von DGL mit konstanten
Koeffizienten: 𝑦 ′ = 𝐴 ⋅ 𝑦(𝑡). Die Matrix 𝐴 sei diagonalisierbar, d.h. es
gibt eine reguläre Matrix 𝑇 und eine Diagonalmatrix 𝐷 = diag(𝜆1 , … , 𝜆𝑛 )
mit 𝑇 −1 𝐴𝑇 = 𝐷. Es folgt dann mit 𝑧 ≔ 𝑇 −1 𝑦 die Äquivalenz von
𝑦 ′ 𝑡 = 𝐴 ⋅ 𝑦 𝑡 ⇔ 𝑇 −1 𝑦 ′ = 𝑇 −1 𝐴𝑇𝑇 −1 𝑦 ⇔ 𝑧 ′ = 𝑇 −1 𝐴𝑇𝑧 = 𝐷𝑧
Die Gleichungen des transformierten Systems sind entkoppelt und
daher lässt sich der skalare Stabilitätsbegriff aus Def. 6.14 auf Systeme
von DGL übertragen. Die Stabilität muss dann für jede Komponente
gewährleistet sein.
Ein Problem tritt auf wenn die Eigenwerte stark unterschiedliche
Größenordnungen haben. Solche DGL nennt man steif.
Numerische Mathematik II
Herbsttrimester 2012
42
Def. 6.14 Man bezeichnet die lineare DGL 𝑦 ′ = 𝐴 ⋅ 𝑦 𝑡 als steif, wenn
sie Komponenten enthält deren Lösung für wachsendes 𝑡 abklingen,
jedoch mit sehr unterschiedlicher Geschwindigkeit:
max Re 𝜆𝑖 : Re 𝜆𝑖 < 0 |
𝑖
≫1
min Re 𝜆𝑗 : Re 𝜆𝑗 < 0 |
𝑗
Bemerkungen:
 In der Praxis hat man oftmals mit nichtlinearen DLG zu tun. In
diesem Fall kann man die DGL 𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 linearisieren. Sei
o.B.d.A. 𝑦 ′ 𝑡 = 𝑓 𝑦 𝑡 ⇒ 𝑦 ′ 𝑡 ≈ 𝑓 𝑦 𝜏 + 𝐽𝑓 𝑦 𝜏 ⋅ 𝑦 𝑡 − 𝑦 𝜏
Dabei bezeichne 𝐽𝑓 die Jacobi Matrix der vektorwertigen Funktion
𝑓. Relevant sind dann die Eigenwerte der Jacobimatrix.
 Die Eigenwerte der Matrix 𝐽𝑓 charakterisieren das Verhalten der
ursprünglichen Lösung nicht immer mit hinreichender Genauigkeit.
 Die Definition von Steifheit ist nicht einheitlich in der Literatur.
 Die Bezeichnung steif rührt von der Betrachtung mechanischer
Systeme (z.B. steife Federn).
Numerische Mathematik II
Herbsttrimester 2012
43
Bsp. 6.17 Betrachten wir das DGL System
𝑦1′ = −100𝑦1
𝑦1 0 = 1
𝑦2′ = −2𝑦2 + 𝑦1 𝑦2 0 = 1
Mit der exakten Lösung (siehe Abbildung rechts)
1 −100𝑡 99 −2𝑡
−100𝑡
𝑦1 𝑡 = 𝑒
𝑦2 𝑡 = − 𝑒
+
𝑒
98
98
1
y1
0.9
0.8
y2
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
−100
0
sind −2, −100.
1
−2
Die erste Gleichung erfordert also einen Zeitschritt von ℎ < 2/100. Man
würde vermuten, dass die zweite Gleichung für 𝑡 > 0.1 einen Zeitschritt
ℎ < 2/2 verlangt. Dass dies nicht der Fall ist zeigt
die Abbildung rechts. Bei der numerischen Berechnung wurde der Zeitschritt ab 𝑡 = 0.1 erhöht. Obwohl die Lösung 𝑦1 schon sehr klein ist muss zur
Gewährleistung der Stabilität das Zeitschrittkriterium des dominierenden Eigenwertes eingehalten werden, sonst explodiert die Lösung. Abhilfe
schaffen hier implizite Verfahren.
Die Eigenwerte der Matrix
5
4
3
2
1
0
-1
-2
0
Numerische Mathematik II
Herbsttrimester 2012
0.05
0.1
0.15
0.2
0.25
0.3
44
Automatische Schrittweitenwahl
Wie bei der numerischen Quadratur kommt der automatischen
Schrittweitenwahl auch bei der Lösung von Differenzialgleichungen
eine große Bedeutung zu. Das Vorgehen ist sehr ähnlich zur
numerischen Integration:
 Zunächst spezifiziert man die gewünschte Genauigkeit in einer
geeigneten Norm, z.B. als absoluten Fehler 𝑦 𝑡 − 𝑢 𝑡 = 𝜀|𝑡 − 𝑡0 |
oder relativen Fehler 𝑦 𝑡 − 𝑢 𝑡 = 𝜀 𝑡 − 𝑡0 ‖𝑦 𝑡 ‖.
 Dann beschafft man sich einen Fehlerschätzer. Hier gibt es wieder
zwei Varianten:
 Schätzung des Fehlers durch zwei Verfahren unterschiedlicher
Ordnung, oder
 Schätzen des Fehlers unter Benutzung unterschiedlicher
Schrittweiten
Numerische Mathematik II
Herbsttrimester 2012
45
Variante I: Variable Schrittweite
Sei 𝑧 die exakte Lösung der DGL durch 𝑡𝑘 , 𝑢𝑘 . Wir berechnen eine
Näherungslösung 𝑢𝑘+1 mittels eines Schrittes der Länge 2ℎ und eine
Näherung 𝑢𝑘+1 mittels zwei Schritten der Länge ℎ. Für ein Verfahren
der Ordnung 𝑝 gilt dann:
𝑧 𝑡𝑘 + 2ℎ − 𝑢𝑘+1
≈ 𝜏𝑝 2ℎ 𝑝 ,
𝑧 𝑡𝑘 + 2ℎ − 𝑢𝑘+1 ≈ 2ℎ(𝜏𝑝 ℎ𝑝 )
2ℎ
Subtraktion liefert
𝑢𝑘+1 −𝑢𝑘+1
2ℎ
= (2𝑝 − 1)𝜏𝑝 ℎ𝑝 daraus folgt die
Abschätzung des lokalen Fehlers: Δ ≔ 𝜏𝑝 ℎ𝑝 =
𝑢𝑘+1 −𝑢𝑘+1
2ℎ
⋅
1
(2𝑝 −1)
Falls gilt Δ ≤ 𝜀 kann der Schritt akzeptiert werden. Andernfalls muss die
Schrittweite verkleinert werden um den lokalen Fehler zu verringern.
Dazu betrachte man den Übergang von einem Schritt der Länge ℎ zu
einem Schritt der Länge 𝛾ℎ. Dann gilt für den lokalen Fehler
𝑝
𝜏𝑝 (𝛾ℎ)𝑝 = 𝛾 𝑝 Δ ≤ 𝜀 ⇔ 𝛾 = 𝜀/Δ
Numerische Mathematik II
Herbsttrimester 2012
46
Variante II
Die zweite Variante besteht darin zwei Verfahren unterschiedlicher
Ordnung zu Verwenden, z.B.
𝑧 𝑡𝑘 + ℎ − 𝑢𝑘+1
𝑧 𝑡𝑘 + ℎ − 𝑢𝑘+1
𝑝
≈ 𝜏𝑝 ℎ ,
≈ 𝜏𝑝+1 ℎ𝑝+1
ℎ
ℎ
Es folgt unter der Annahme 𝜏𝑝 ℎ𝑝 ≫ 𝜏𝑝+1 ℎ𝑝+1
𝑢𝑘+1 − 𝑢𝑘+1
Δ: =
≈ 𝜏𝑝 ℎ𝑝 − 𝜏𝑝+1 ℎ𝑝+1 ≈ 𝜏𝑝 ℎ𝑝 ⇒ 𝜏𝑝 ≈ Δ/ℎ𝑝
ℎ
Beim Übergang von einem Schritt der Länge ℎ zu einem Schritt der
Länge 𝛾ℎ erzielt das Verfahren der Ordnung 𝑝 einen Fehler von
𝑝
Δ
𝜏𝑝 𝛾ℎ 𝑝 ≈ 𝑝 𝛾ℎ 𝑝 = Δ𝛾 𝑝 . Wiederum gilt 𝛾 𝑝 Δ ≤ 𝜀 ⇔ 𝛾 = 𝜀/Δ
ℎ
Bemerkungen:
 Für beide Varianten wird der Schritt akzeptiert wenn der lokale
Fehler klein genug ist. Anderenfalls wird er verworfen und mit dem
kleineren Zeitschritt wiederholt.
 Wenn die Näherung akzeptiert wird, wird trotzdem der Zeitschritt
angepasst (vergrößert) für die nächste Iteration.
Numerische Mathematik II
Herbsttrimester 2012
47
Mehrschrittverfahren
Def. 6.15 Mehrschrittverfahren
Ein 𝑝-Schritt Verfahren 𝑝 ≥ 1 ist eines bei dem 𝑢𝑛+1 von 𝑢𝑛+1−𝑝
abhängt aber nicht von Werten 𝑢𝑘 mit 𝑘 < 𝑛 + 1 − 𝑝.
Wir betrachten im Folgenden nur lineare Mehrschrittverfahren. Sie sind
von der Form:
𝑝−1
𝑢𝑛+1 =
𝑝−1
𝑎𝑗 𝑢𝑛−𝑗 + ℎ
𝑗=0
𝑏𝑗 𝑓𝑛−𝑗 + 𝑏−1 𝑓𝑛+1 für 𝑢𝑝 , 𝑢𝑝+1 …
𝑗=0
Die Koeffizienten sind reell und es gilt 𝑎𝑝−1 ≠ 0 oder 𝑏𝑝−1 ≠ 0. Ist
𝑏−1 ≠ 0 erhält man ein implizites Verfahren, ansonsten ein explizites
Verfahren.
Bemerkungen:
 Für 𝑝 = 1 erhält man ein Einschrittverfahren
 Man benötigt Startwerte 𝑢0 , … , 𝑢𝑝−1
Numerische Mathematik II
Herbsttrimester 2012
48
Es gibt eine Reihe bekannter Familien von Mehrschrittverfahren:
 Adams-Verfahren entstehen indem wir 𝑎0 = 1, 𝑎𝑗 = 0, 𝑗 ≥ 1 setzen
𝑝−1
𝑢𝑛+1 = 𝑢𝑛 + ℎ
𝑏𝑗 𝑓𝑛−𝑗
𝑗=−1
Im expliziten Fall (𝑏−1 = 0) heißen Sie Adams-Bashforth Verfahren im
impliziten Fall (𝑏−1 ≠ 0) Adams-Moulton Verfahren. Im impliziten Fall ist
auch 𝑝 = 0 erlaubt.
Adams Verfahren sind konsistent wenn gilt: 𝑏𝑗 = 1 vgl. Def. 6.9)
In beiden Fällen erhält man die Koeffizienten aus der
𝑡
Integraldarstellung 𝑦 𝑡𝑛+1 = 𝑦(𝑡𝑛 ) + 𝑡 𝑛+1 𝑓 𝜏, 𝑦 𝜏 𝑑𝜏. Anstatt 𝑓 wird
𝑛
das Interpolationspolynom integriert, welches im expliziten Fall in den
Punkten 𝑡𝑖 , 𝑓𝑖 𝑖 = 𝑛 + 1 − 𝑝, … , 𝑛 interpoliert und im expliziten Fall in
den Punkten 𝑡𝑖 , 𝑓𝑖 𝑖 = 𝑛 + 1 − 𝑝, … , 𝑛 + 1. Dabei wird eine
äquidistante Diskretisierung 𝑡𝑗 = 𝑡0 + 𝑗ℎ vorausgesetzt, was eine nicht
unerhebliche Einschränkung darstellt.
Numerische Mathematik II
Herbsttrimester 2012
49
Die BDF Verfahren (Backward Differencing) erhält man durch setzen
von 𝑏−1 ≠ 0, 𝑏𝑗 = 0, 𝑗 ≥ 0.
𝑝−1
𝑢𝑛+1 =
𝑎𝑗 𝑢𝑛−𝑗 + ℎ𝑏−1 𝑓𝑛+1
𝑗=0
Bei den BDF Methoden erhalten wir die Koeffizienten 𝑎𝑗 indem wir in
𝑦 ′ 𝑡 = 𝑓 𝑡, 𝑦 𝑡 die erste Ableitung 𝑦 ′ 𝑡𝑛+1 ersetzen durch die erste
Ableitung des Interpolationspolynoms vom Grad 𝑝 in den 𝑝 + 1 Knoten:
𝑡𝑖 , 𝑢𝑖 𝑖 = 𝑛 + 1 − 𝑝, … , 𝑛 + 1.
Bemerkungen:
 Die Konsistenz von BDF Verfahren und im Allgemeinen von
Mehrschrittverfahren ist nicht so leicht zu sehen wie im Fall der
Adams Verfahren.
 Insbesondere folgt aus der Konsistenz eines Mehrschrittverfahrens
nicht automatisch die Konvergenz im Gegensatz zu den
Einschrittverfahren.
Numerische Mathematik II
Herbsttrimester 2012
50
Satz 6.16 Das Mehrschrittverfahren ist genau dann konsistent wenn die
folgenden Bedingungen erfüllt sind:
𝑝−1
𝑝−1
𝑎𝑗 = 0 und
𝑗=0
−
𝑝−1
𝑗𝑎𝑗 +
𝑗=0
𝑏𝑗 = 1
𝑗=−1
Satz 6.17 Ein konsistentes Mehrschrittverfahren ist genau dann
nullstabil wenn es die sogenannte Wurzelbedingung erfüllt:
𝑝−1
Sei hierzu 𝜌 𝑟 ≔ 𝑟 𝑝 − 𝑗=0 𝑎𝑗 𝑟 𝑝−𝑗 das erste charakteristische
Polynom des Verfahrens. Das Mehrschrittverfahren erfüllt die Wurzelbedingung wenn alle Wurzeln 𝑟𝑖 innerhalb des Einheitskreises in der
komplexen Ebene mit Mittelpunkt 0 liegen und wenn alle auf den Rand
fallenden Wurzeln einfach sind: |𝑟𝑖 ≤ 1 und 𝜌′ 𝑟𝑖 ≠ 0 falls |𝑟𝑖 = 1 .
Satz 6.18 (Lax-Richtmyer)
Ein konsistentes Mehrschrittverfahren ist genau dann konvergent wenn
es nullstabil ist und wenn der Fehler in den Anfangsdaten für ℎ gegen
Null gegen Null strebt.
Numerische Mathematik II
Herbsttrimester 2012
51
Bsp. 6.18
𝑝−1
 Adams Bashforth Verfahren: aus 𝑢𝑛+1 = 𝑢𝑛 + ℎ 𝑗=0 𝑏𝑗 𝑓𝑛−𝑗
erhalten wir für 𝑝 = 1: 𝑢𝑛+1 = 𝑢𝑛 + ℎ𝑓𝑛
Für 𝑝 = 2 sei 𝑃 das Polynom welches in den Knoten
𝑓 −𝑓
𝑡𝑛 , 𝑡𝑛−1 interpoliert: 𝑃 𝑡 = 𝑓𝑛−1 + 𝑡 − 𝑡𝑛−1 𝑛 𝑛−1 dann gilt
𝑡𝑛 −𝑡𝑛−1
𝑃 𝑡𝑛+1 = 2 𝑓𝑛 − 𝑓𝑛−1 , da 𝑡𝑛+1 − 𝑡𝑛−1 = 2(𝑡𝑛 −𝑡𝑛−1 )
Offenbar gilt für das Integral
𝑡𝑛+1
ℎ
ℎ
𝑃 𝜏 𝑑𝜏 = 𝑃 𝑡𝑛+1 + 𝑃 𝑡𝑛 = 3 𝑓𝑛 − 𝑓𝑛−1
2
2
𝑡𝑛
Insgesamt erhält man das Zweischritt- Verfahren
ℎ
𝑢𝑛+1 = 𝑢𝑛 + 3 𝑓𝑛 − 𝑓𝑛−1
2
Das Adams Bashforth Dreischritt-Verfahren lautet (siehe Übung)
ℎ
𝑢𝑛+1 = 𝑢𝑛 +
23 𝑓𝑛 − 16𝑓𝑛−1 + 5𝑓𝑛−2
12
Numerische Mathematik II
Herbsttrimester 2012
52
 Bsp 6.19
𝑝−1
Adams Moulton Verfahren: aus 𝑢𝑛+1 = 𝑢𝑛 + ℎ 𝑗=−1 𝑏𝑗 𝑓𝑛−𝑗
erhalten wir für 𝑝 = 0: 𝑢𝑛+1 = 𝑢𝑛 + ℎ𝑓𝑛+1
Für 𝑝 =1 sei 𝑃 das Polynom welches in den Knoten
𝑡𝑛 , 𝑡𝑛+1 interpoliert 𝑃 𝑡𝑛+1 = 𝑓𝑛+1 , 𝑃 𝑡𝑛 = 𝑓𝑛 und
𝑡𝑛+1
ℎ
𝑃
𝜏
𝑑𝜏
=
𝑓𝑛+1 + 𝑓𝑛 . Insgesamt erhält man
𝑡
𝑛
ℎ
2
2
𝑢𝑛+1 = 𝑢𝑛 + 𝑓𝑛+1 + 𝑓𝑛 also das Crank-Nicolson Verfahren.
Für 𝑝 =2 interpoliert man in den Knoten 𝑡𝑛−1, 𝑡𝑛 , 𝑡𝑛+1 und berechnet
𝑡
das Integral 𝑡 𝑛+1 𝑃 𝜏 𝑑𝜏 mit der Simpson Regel. Man erhält:
𝑛
ℎ
𝑢𝑛+1 = 𝑢𝑛 +
5 𝑓𝑛+1 + 8𝑓𝑛 − 𝑓𝑛−1
12
Eine Fixpunktiteration für das obige Verfahren lautet:
ℎ
(𝑘+1)
(𝑘)
𝑢𝑛+1 = 𝑢𝑛 +
5𝑓(𝑡𝑛+1 , 𝑢𝑛+1 ) + 8𝑓𝑛 − 𝑓𝑛−1
12
Zum Abschluss noch ein Verfahren vierter Ordnung:
ℎ
𝑢𝑛+1 = 𝑢𝑛 +
9 𝑓𝑛+1 + 19𝑓𝑛 − 5𝑓𝑛−1 + 𝑓𝑛−2
24
Numerische Mathematik II
Herbsttrimester 2012
53
 Bsp 6.20 Ohne Herleitung drei Beispiele für BDF Verfahren:
𝑢𝑛+1 = 𝑢𝑛 + ℎ𝑓𝑛+1
1
2ℎ
𝑢𝑛+1 = (4𝑢𝑛 − 𝑢𝑛−1 ) +
𝑓
3
3 𝑛+1
1
6ℎ
𝑢𝑛+1 =
(18 𝑢𝑛 − 9𝑢𝑛−1 + 2𝑢𝑛−2 ) +
𝑓𝑛+1
11
11
Bemerkungen
 Mehrschrittverfahren erfordern die Speicherung der vorangegangenen Schritte ( nur eine Funktionsauswertung im neuen Schritt)
 Adaptive Zeitschritte sind aufwändig (Koeffizienten ändern sich)
 Im Allgemeinen haben 𝑝-Schritt Adams-Bashforth und BDF
Verfahren die Ordnung 𝑝, Adams-Moulton Verfahren 𝑝 + 1.
 BDF Verfahren haben einen großen Stabilitätsbereich. Sie sind für
die Lösung von steifen Problemen attraktiv.
 Integriert man bei den Adams-Verfahren über ein Intervall der Länge
2ℎ erhält man die expliziten Verfahren von Nyström z.B:
𝑢𝑛+1 ≔ 𝑢𝑛−1 + 2ℎ𝑓𝑛 und Milne Simpson (implizit) z.B.
𝑢𝑛+1 ≔ 𝑢𝑛−1 + ℎ/3(𝑓𝑛−1 + 4𝑓𝑛 + 𝑓𝑛+1 )
Numerische Mathematik II
Herbsttrimester 2012
54
Die folgenden Abbildungen zeigen die äußere Begrenzung des
Stabilitätsbereichs für Adams Bashforth & Adams Moulton Verfahren
bzw. die innere Begrenzung für BDF Verfahren (aus Referenz [7]).
Numerische Mathematik II
Herbsttrimester 2012
55
Bemerkungen:
 Man beachte, dass bei den Adams Verfahren der Stabilitätsbereich
mit steigender Ordnung kleiner wird.
 Bei den BDF Verfahren ist bemerkenswert, dass die negative reelle
Achse immer zum Stabilitätsbereich gehört. Es gibt keine
nullstabilen BDF Verfahren der Ordnung größer 5.
 Es gelten die folgenden Limitierungen für lineare
Mehrschrittverfahren (ohne Beweis)
 Erste Dahlquist Schranke:
Es gibt kein nullstabiles 𝑞-schrittiges lineares
Mehrschrittverfahren der Ordnung größer als 𝑞 + 1 falls
𝑞 ungerade ist und 𝑞 +2 falls 𝑞 gerade ist.
 Zweite Dahlquist Schranke:
Ein lineares explizites Mehrschrittverfahren kann nicht A-stabil
sein. Darüberhinaus gibt es kein A-stabiles lineares (implizites)
Mehrschrittverfahren von höherer als zweiter Ordnung.
Numerische Mathematik II
Herbsttrimester 2012
56
Zusammenfassung
 Bei der Analyse numerischer Verfahren zur Lösung von DGL
unterscheidet man den globalen Fehler und den lokalen Abbruchfehler der durch die Konsistenzordnung charakterisiert wird.
 Wir haben zwei Stabilitätsbegriffe kennengelernt. Die Nullstabilität
sichert die Stabilität des Verfahrens gegenüber kleinen Störungen
für ℎ → 0. Einschrittverfahren sind, Lipschitzstetigkeit vorausgesetzt,
automatisch nullstabil. Dies gilt nicht für Mehrschrittverfahren.
 Absolute Stabilität garantiert die Beschränktheit der Lösung für
konstante Zeitschrittweite und wachsendes Integrationsintervall. Sie
impliziert unter Umständen eine Schrittweitenbegrenzung.
 Nach dem Satz von Lax-Richtmyer impliziert Konsistenz und Nullstabilität die Konvergenz des Verfahrens. Die Bedeutung des Satzes
liegt darin, dass Konvergenz deutlich schwieriger nachzuweisen ist.
 Man unterscheidet explizite und implizite Verfahren. Bei impliziten
Verfahren taucht 𝑢𝑛+1 auf beiden Seiten der Verfahrensvorschrift
auf. Implizite Verfahren haben in der Regel einen deutlich größeren
Stabilitätsbereich sind jedoch aufwändiger in der Auswertung.
Numerische Mathematik II
Herbsttrimester 2012
57
Zusammenfassung
 Das explizite und implizite Euler-Verfahren ist auf Grund der
niedrigen Ordnung für die meisten praktischen Belange ungeeignet.
 Einschrittverfahren haben generell den Vorteil der einfachen Steuerung der Schrittweite. Sie sind auch einfach auszuwerten und zu
programmieren. Des Weiteren sind Sie unter schwachen Voraussetzungen nullstabil.
 Runge-Kutta Verfahren bilden eine sehr große Klasse von Einschrittverfahren. In der Praxis werden am häufigsten explizite RK Verfahren verwendet. Man benötigt jedoch relativ viele Funktionsauswertungen mit wachsender Ordnung. Eingebettete RK Verfahren
bieten effiziente Möglichkeiten der Zeitschrittsteuerung.
 Mehrschrittverfahren (lineare) bieten hohe Ordnung mit wenigen
Funktionsauswertungen. Die Nullstabilität und daher die Konvergenz
sind nicht automatisch gewährleistet und müssen beim Entwurf
beachtet werden. Die Anpassung der Zeitschrittweite ist relativ
komplex. Anlaufwerte müssen durch ein Einschrittverfahren
generiert werden.
Numerische Mathematik II
Herbsttrimester 2012
58
Zusammenfassung
 Steife Systeme zeichnen sich durch stark unterschiedliche
Zeitskalen aus. Der Einsatz expliziter Verfahren ist hier nicht
sinnvoll. Man benötigt Verfahren mit großem Stabilitätsbereich.
 A-stabile Verfahren niedriger Ordnung sind das implizite Euler
Verfahren, das Crank-Nicolson Verfahren und die BDF2
Methode.
 BDF Verfahren höherer Ordnung haben ebenfalls einen großen
Stabilitätsbereich.
 Eine weitere alternative sind implizite RK Verfahren höherer
Ordnung.
Numerische Mathematik II
Herbsttrimester 2012
59