Motivation für adaptive Schrittweite

Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Motivation für adaptive Schrittweite
Ziel: Gegebene Genauigkeit mit möglichst minimalem Aufwand zu erreichen
Idee: Wähle lokal unterschiedliche Schrittweiten
Minimierungsproblem: Bestimme für gegebene Anzahl der Schritte die Verteilung der
Stützstellen, so dass der Fehler minimal wird
Aber: Viel zu teuer
Ausweg: Bestimme die Schrittweite möglichst groß, so dass eine relative lokale
Genauigkeit erfüllt ist
Umsetzung: Bestimme den Fehler durch Vergleich mit einer besseren Lösung
• halbe Schrittweite
• höhere Ordnung
hneu =??
Adaptivität (adapt01)
1
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Adaptives Verfahren: Berechnung der neuen Schrittweite
nach Dahmen-Reusken
p : Ordnung des Verfahrens
r
hTOL
α=β
EST
α = min{α, αmax}
p
α = max{α, αmin}
hneu = αh
hneu = min{hneu, hmax}
hneu = max{hneu, hmin}
Validierung: Ist EST ≤ hTOL oder h = hmin?
Adaptivität (adapt20)
2
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
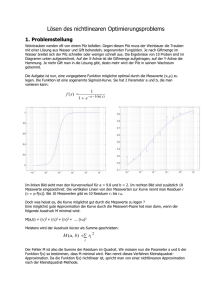
Eingebettetes RK4(3)–Verfahren
y ′ = y, y(0) = 1
exakte Loesung
3
Knoten und lokale Schrittweite
TOL = 1e−6
−1
10
2
h
y
2.5
1.5
1
0
−2
0.2
0.4
t
0.6
0.8
1
10
0
0.2
0.4
t
0.6
0.8
1
Beobachtung: Geringe Schwankungen in der Schrittweite
Adaptivität (adapt02)
3
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Eingebettetes RK4(3)–Verfahren
y ′ = −200ty 2, y(0) = 1
exakte Loesung
1
−1
10
Knoten und lokale Schrittweite
TOL = 1e−5
0.8
y
h
0.6
0.4
−2
10
0.2
0
0
0.2
0.4
t
0.6
0.8
1
0
0.2
0.4
t
0.6
0.8
1
Beobachtung: Starke Schwankungen in der Schrittweite
Adaptivität (adapt03)
4
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Eingebettetes RK4(3)–Verfahren
y ′ = −sgn(t)y, y(−1) = 1/e
exakte Loesung
1
−1
10
Knoten und lokale Schrittweite
TOL = 1e−5
0.8
−2
10
y
h
0.6
−3
10
0.4
0.2
−1
−4
−0.5
t
0
0.5
1
10
−1
−0.5
t
0
0.5
1
Beobachtung: Algorithmus erkennt die Singularität;
Vorgabe von minimaler Schrittweite verhindert “Festfressen”
Adaptivität (adapt04)
5
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Eingebettetes RK4(3)–Verfahren
Restringiertes Dreikörperproblem (1)
1.5
1.5
TOL=0.1−>#f=421
1.5
TOL=0.01−>#f=741
TOL=0.001−>#f=1809
1
1
1
0.5
0.5
0.5
0
0
0
−0.5
−0.5
−0.5
−1
−1
−1
−1.5
−1.5
0
adaptiv RK4(3)
−1
−0.5
5
0
0.5
10
15
havg = 2.8 · 10−1
0
adaptiv RK4(3)
−1
−0.5
5
0
0.5
10
havg = 1.5 · 10−1
hmin = 1.7 · 10
0
hmax = 6.1 · 10
hmax = 1.0 · 10
1
15
−5
hmin = 3.0 · 10
Adaptivität (adapt05)
1
−1.5
−1.5
−1.5
−1.5
0
adaptiv RK4(3)
−1
−0.5
5
0
0.5
10
1
15
havg = 6.5 · 10−2
−5
hmin = 9.6 · 10
−6
−1
hmax = 3.3 · 10
−1
6
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Runge–Kutta: adaptiv vs. äquidistant
Restringiertes Dreikörperproblem, Fehler e(T )
0
10
−2
10
−4
Fehler
10
−6
10
−8
10
adaptiv
aequidistant
−10
10
2
10
3
10
4
10
5
10
6
10
Anzahl der Funktionsauswertungen
Blau: Standard RK 4–Verfahren, Rot: eingebettetes RK4(3)–Verfahren
Für einen Fehler in der Größenordnung von 1 km benötigt das äquidistante Verfahren mit 384000
Funktionsauswertungen über 60mal mehr als das adaptive (6261).
Adaptivität (adapt11)
7
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Runge–Kutta: adaptiv vs. äquidistant
Restringiertes Dreikörperproblem
1.5
60
#f = 741
#f = 1000
40
1
20
0.5
0
0
−20
−0.5
−40
−1
−60
adaptiv RK4(3)
RK 4
−40
−20
0
20
40
60
−1.5
−1.5
−1
−0.5
0
0.5
1
Blau: Äquidistante Punkte,
Rot: Adaptive Punkte,
bei ähnlicher Anzahl von Funktionsauswertungen.
Adaptivität (adapt12)
8
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Eingebettetes RK4(3)–Verfahren
Restringiertes Dreikörperproblem (2)
1.5
1.5
TOL=0.1−>#f=369
1.5
TOL=0.01−>#f=673
TOL=0.001−>#f=1653
1
1
1
0.5
0.5
0.5
0
0
0
−0.5
−0.5
−0.5
−1
−1
−1
−1.5
−1.5
0
adaptiv RK4(3)
−1
2
−0.5
4
0
0.5
6
8
havg = 1.9 · 10−1
10
0
adaptiv RK4(3)
−1
2
−0.5
4
0
0.5
6
8
havg = 1.1 · 10−1
−5
hmin = 1.6 · 10
−1
hmax = 6.7 · 10
hmin = 3.0 · 10
hmax = 8.4 · 10
Adaptivität (adapt06)
1
−1.5
−1.5
1
10
−1.5
−1.5
0
adaptiv RK4(3)
−1
2
−0.5
4
0
0.5
6
8
1
10
havg = 4.8 · 10−2
−5
hmin = 9.3 · 10
−6
−1
hmax = 3.6 · 10
−1
9
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Lokale Schrittweite
Dreikörper-Problem
TOL = 1e-2
TOL = 1e-3
Eingebettetes Runge−Kutta Verfahren RK4(3)
Eingebettetes Runge−Kutta Verfahren RK4(3)
2
2
1
1
0
0
−1
−1
−2
−2
TOL = 1e−02, Schritte = 10717
−1
0
1
−2
−2
Schrittweite
0
TOL = 1e−03, Schritte = 38897
−1
1
Schrittweite
0
10
0
10
−1
−1
10
10
−2
−2
10
10
−3
−3
h
10
h
10
−4
−4
10
10
−5
−5
10
10
−6
−6
10
10
−7
10
−7
0
Adaptivität (adapt16)
5
10
15
t
20
25
10
0
5
10
15
t
20
25
10
Prof. Dr. Barbara Wohlmuth
Lehrstuhl für Numerische Mathematik
Eingebettetes RK4(3)–Verfahren
Restringiertes Dreikörperproblem (3)
1.5
1.5
TOL=0.1−>#f=405
1.5
TOL=0.01−>#f=821
TOL=0.001−>#f=1813
1
1
1
0.5
0.5
0.5
0
0
0
−0.5
−0.5
−0.5
−1
−1
−1
−1.5
−1.5
0
adaptiv RK4(3)
−1
1
−0.5
2
0
3
0.5
1
−1.5
−1.5
4
5
0
havg = 8.8 · 10−2
−1
1
−0.5
2
0
3
hmin = 1.5 · 10
−1
hmax = 4.5 · 10
hmax = 8.6 · 10
0.5
1
−1.5
−1.5
4
5
0
havg = 4.5 · 10−2
−5
hmin = 2.7 · 10
Adaptivität (adapt07)
adaptiv RK4(3)
adaptiv RK4(3)
−1
1
−0.5
2
0
3
0.5
1
4
5
havg = 2.1 · 10−2
−5
hmin = 8.6 · 10
−6
−1
hmax = 2.5 · 10
−1
11