Punkt-in-Polygon-Suche Übersicht

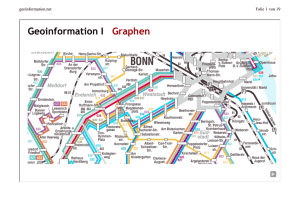
geoinformation.net
Punkt-in-Polygon-Suche Übersicht
l
l
Praxisbeispiel/Problemstellung
Zählen von Schnittpunkten
Schnitt einer Halbgerade mit der Masche
Aufwandsbetrachtung
Streifenkarte
Vorgehen und Eigenschaften
Speicherung der Daten / Suche in den Daten
Aufwandsbetrachtung
Trapezkarte
¡
¡
l
¡
¡
¡
l
Folie 1 von 19
geoinformation.net
Praxisbeispiel Rollover am Bildschirm
Folie 2 von 19
geoinformation.net
Folie 3 von 19
Problemstellung 1 In welcher Masche liegt Punkt P?
Allgemein:
Gegeben ist eine räumliche
Datenbank und eine Klasse typischer
Anfragen
Gesucht wird eine Datenstruktur, die
einen effizienten Algorithmus
unterstützt
l
l
Konkret:
Gegeben ist eine Landkarte S und ein
Punkt P
Gesucht wird die Masche M, die den
Punkt P beinhaltet
l
l
geoinformation.net
Folie 4 von 19
Lösungsansatz 1 Halbgerade am Punkt anlegen
Aus dem >>Jordanschen Kurvensatz
folgt:
l
l
l
1x
Konstruiere ausgehend von P eine
Halbgerade in beliebiger Richtung
P liegt außerhalb des begrenzten
Gebietes, wenn eine gerade Anzahl
von Schnittpunkten entsteht.
P liegt innerhalb des begrenzten
Gebietes, wenn eine ungerade
Anzahl von Schnittpunkten entsteht.
geoinformation.net
Folie 5 von 19
Theorem Jordanscher Kurvensatz
Nach Jordan:
l
l
Eine geschlossene Jordankurve S
zerlegt die Ebene in zwei
zusammenhängende Gebiete, von
denen genau eines nicht beschränkt
ist.
Zwei Punkte der Ebene können genau
dann durch eine Jordankurve J
verbunden werden, die S nicht
schneidet, wenn sie entweder beide
im Inneren oder beide im Äußeren
von S liegen.
geoinformation.net
Folie 6 von 19
Lösungsansatz 1 Suchaufwand
Das Verfahren muss für jede Masche
iteriert werden:
l
l
Aufwand für ein Polygon mit n
Kanten: O(n)
Aufwand bei m Polygonen: O(m*n)
Der Aufwand für eine Suche nach dem
Jordanschen Kurvensatz beträgt
O(m*n).
Mit welchem Verfahren kann der
Suchaufwand verringert werden?
geoinformation.net
Folie 7 von 19
Praxisbeispiel Bundesrepublik Deutschland
In der Praxis kann die Anzahl der Maschen und Kanten sehr schnell hoch werden:
Bundesrepublik Deutschland:
1 Masche
Bundesländer:
16 Maschen mit 17.700 Kanten
Kreise:
440 Maschen mit 75.000 Kanten
Gemeinden:
13.900 Maschen mit 300.000 Kanten
Angaben für den Massstab 1:500.000 Quelle: ArcDeutschland 500, ESRI
geoinformation.net
Folie 8 von 19
Vorgehensweise 2 Konstruktion eines Index
Der Aufbau eines Index kostet Zeit. Diese
amortisiert sich jedoch bei der Abfrage.
Allgemein:
Gegeben: Räumliche Datenbank und
eine Klasse typischer Anfragen
Gesucht: Datenstruktur, die einen
möglichst schnellen Algorithmus
unterstützt
Konkret:
Gegeben: Landkarte S und ein Punkt P
Gesucht: Index für die schnelle
Identifikation der zugeordneten
Masche M .
l
l
l
l
geoinformation.net
Folie 9 von 19
Lösungsansatz 2 Konstruktion der Streifenkarte S'
Vorgehen:
l
Konstruktion einer Karte S' durch
Aufteilung der Landkarte mit
vertikalen Geraden durch alle
Knoten.
Folge:
l
2x
In allen Schnittpunkten der Geraden
mit den Kanten entstehen neue
Knoten.
geoinformation.net
Folie 10 von 19
Lösungsansatz 2 Eigenschaften von S'
S' hat folgende Eigenschaften:
l
l
2x
Die Maschen sind in Trapeze (ggf.
Dreiecke) zerlegt.
Kanten sind in Teilkanten zerlegt.
geoinformation.net
Folie 11 von 19
Lösungsansatz 2 Vorteil von S'
Die Karte erhält eine Struktur, die wir
ausnutzen können:
l
l
2x
Die Streifen sind in x-Richtung
angeordnet.
Innerhalb eines Streifens sind die
Teilkanten und damit die Trapeze in
y-Richtung angeordnet.
geoinformation.net
Folie 12 von 19
Lösungsansatz II Speicherung der Daten
Die Datenspeicherung erfolgt in Arrays:
l
l
Ein Array enthält die x-Koordinaten
der Streifen.
Jeder Streifen enthält ein Array der
y-Koordinaten der Teilkanten.
geoinformation.net
Folie 13 von 19
Lösungsansatz 2 Intervall-Bisektion
Zwei schnelle binäre Suchalgorithmen
werden für die Suche nach der Masche
hintereinander geschaltet:
l
l
Binäre Suche im Array der xKoordinaten nach dem Streifen, der P
enthält.
Binäre Suche nach dem zugehörigen
Trapez in diesem Streifen.
Sobald die Teilkante direkt >>unterhalb/
oberhalb von P gefunden ist, ist die
gesuchte Masche gefunden.
3x
geoinformation.net
Folie 14 von 19
Bemerkungen Eigenschaften der Maschen
Es gilt:
l
l
l
Jeder Abschnitt eines Streifens liegt
genau in einer Masche.
Jede Kante lässt sich einer in yRichtung folgenden Masche zuordnen.
Die Fläche"Außen" muss ebenfalls als
Masche angesehen werden.
geoinformation.net
Folie 15 von 19
Lösungsansatz 2 Suchaufwand
Der Suchaufwand dieses Lösungsansatzes entsteht durch:
l
l
Binäre Suche im Array der x-Koordinaten nach dem Streifen, der P enthält:
Binäre Suche in einem Array mit maximaler Länge 2n: O(log n)
Binäre Suche nach der Lage von P zu den Teilkanten im Array der y-Koordinaten:
Binäre Suche in einem Array mit maximaler Länge n: O(log n)
Der Aufwand für die binäre Suche in einer Streifenkarte beträgt O(log n).
Im >>Vergleich zum Lösungsansatz 1 hat sich der Suchaufwand verbessert.
geoinformation.net
Folie 16 von 19
Vergleich Suchaufwand der zwei Lösungsansätze
Der Aufwand für eine Suche nach dem
Jordanschen Kurvensatz beträgt O(n).
Der Suchaufwand für die binäre Suche in
einer Streifenkarte beträgt O(log n).
geoinformation.net
Folie 17 von 19
Lösungsansatz 2 Speicherbedarf
Es entsteht eine hohe Speicheranforderung durch:
l
l
die sortierte Speicherung der x-Koordinaten der vertikalen Geraden in einem
Array:
Array der x-Koordinaten: O(n)
die sortierte Speicherung der y-Koordinaten der Teilkanten jedes Streifens von
oben nach unten in einem Array:
Array der y-Koordinaten: O(n)
Die Speicheranforderung für die Daten dieses Lösungsansatzes beträgt O(n²)
geoinformation.net
Folie 18 von 19
Lösungsansatz 2 Worst Case Speicherbedarf
Der Worst Case tritt tatsächlich auf:
l
In ungünstigen Fällen erfolgt mit
diesem Verfahren eine sehr hohe
Knoten- und Teilkantenbildung und
damit ein hohes Datenaufkommen.
Wie kann der Speicherbedarf verringert
werden?
1x
geoinformation.net
Folie 19 von 19
Problemstellung 3 Verringerung des Speicherbedarfs
Zwischenresümee:
l
l
Die Zerlegung in Streifen führt zu
einer schnellen Suche.
Allerdings ist der Speicherbedarf
unvertretbar hoch.
Problem:
l
Gibt es eine bessere Zerlegung, die
die Laufzeit erhält und den
Speicherbedarf verringert?