- Fachgebiet Datenbanken und Informationssysteme

Erweiterung eines objektrelationalen
Datenbankmanagementsystems um räumliche
Verbunde
Diplomarbeit im Rahmen des Studienganges
Mathematik mit Studienrichtung Informatik
vorgelegt von Oliver Schweer
Universität Hannover - Fachbereich Informatik
Institut für Informationssysteme
Fachgebiet Datenbanksysteme
Prüfer: Prof. Dr. U. Lipeck
Zweitprüfer: Prof. Dr. R. Parchmann
Hannover, 27. Juni 2003
Inhaltsverzeichnis
1 Einleitung
1
2 Verbunde in Datenbanken
2.1 Verbund ohne Index . . . . . . . . . . . . . . . . .
2.2 Indexe in Datenbanken . . . . . . . . . . . . . . . .
2.2.1 B*-Bäume . . . . . . . . . . . . . . . . . . .
2.2.2 Hash-Index . . . . . . . . . . . . . . . . . .
2.2.3 Bitmap-Listen . . . . . . . . . . . . . . . . .
2.2.4 Verallgemeinerte Zugriffspfadstruktur . . . .
2.3 Indexgestützter Verbund . . . . . . . . . . . . . . .
2.3.1 Verbundindexe . . . . . . . . . . . . . . . .
2.3.2 Verbunde in objektrelationalen Datenbanken
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
4
5
6
9
14
15
17
17
19
3 Spatial Join Algorithmen
3.1 indexed nested loops join . . . . . . . . . . . . . . . . . . . . .
3.2 R*-tree join . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1 Aufbau eines R-Baumes . . . . . . . . . . . . . . . . .
3.2.2 Spatial Join . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Seeded Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1 Seeded Tree Konstruktion . . . . . . . . . . . . . . . .
3.4 Spatial Hash-Join . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Funktionsweise des Hash-Joins . . . . . . . . . . . . . .
3.4.2 Beispiele für Zuweisungs- und Ausdehnungsfunktionen
3.5 Z-Codes und Standard-Indexe . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
20
21
21
22
24
25
27
27
28
30
.
.
.
.
.
.
.
36
37
41
41
42
43
43
45
4 GiST-Indexe
4.1 Überblick über GiST . . . . . . . . . . . . . .
4.2 libgist der University of California at Berkeley
4.2.1 GiST-Erweiterungen . . . . . . . . . .
4.2.2 Funktionsübersicht . . . . . . . . . . .
4.2.3 Klassenübersicht . . . . . . . . . . . .
4.2.4 Suchbaumerweiterungen . . . . . . . .
4.2.5 Einschränkungen der libgist . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5 GiST Indexe für Oracle
5.1 Oracle - Extensible Indexing Interface . . . . . . . .
5.1.1 Methoden des Extensible Indexing Interface
5.2 OraGIST-Bibliothek . . . . . . . . . . . . . . . . .
5.2.1 Änderungen an der libgist . . . . . . . . . .
5.2.2 Struktur der Implementierung . . . . . . . .
5.2.3 Die Klasse OraGiST . . . . . . . . . . . . . .
5.3 Oracle - Pipelined Table Functions . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
47
47
48
50
50
51
52
54
6 Entwurf des Verbund-Algorithmus
6.1 Vorüberlegungen . . . . . . . . . . . . .
6.2 Verbundalgorithmen für GiST . . . . . .
6.2.1 Einfacher GiST-Verbund . . . . .
6.2.2 Zusätzliche Selektionen . . . . . .
6.2.3 Verbundalgorithmus für die libgist
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
57
58
59
60
60
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7 JoinGiST
7.1 Struktur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2 Methoden der JoinGiST-Klassen . . . . . . . . . . . . . . . . .
7.2.1 JoinGiST parameters . . . . . . . . . . . . . . . . . . .
7.2.2 JoinGiST ext t . . . . . . . . . . . . . . . . . . . . . .
7.2.3 JoinGiST . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.4 odci2join - Schnittstelle zwischen JoinGiST und Oracle
7.3 Einschränkungen . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.1 Cursorerweiterung . . . . . . . . . . . . . . . . . . . .
7.3.2 Compiler . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.3 Speicherort der Indexdaten . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
63
63
64
64
66
67
69
70
70
70
71
8 Anwendung und Performance
8.1 Anwendung . . . . . . . . . . . . . . . .
8.1.1 Formulierung von Anfragen . . .
8.1.2 Weitere Verbunde . . . . . . . . .
8.2 Praktisches Beispiel mit Performance . .
8.3 Performance-Analyse . . . . . . . . . . .
8.4 Ausblick und Verbesserungsmöglichkeiten
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
72
72
72
73
73
75
75
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A Beispiel einer OraGiST-Erweiterung
77
B Beispiel einer JoinGiST-Erweiterung
92
Kapitel 1
Einleitung
In objektrelationalen Datenbankmanagementsystemen (ORDBMS) besteht die Möglichkeit, komplexe Datenstrukturen mit zugehörigen Methoden zu verwalten. So ist es unter
anderem möglich, geographische Daten in den Tabellen einer Datenbank abzulegen und
verschiedene Operationen darauf anzuwenden. Eine dieser Operationen ist der räumliche Verbund (spatial join), wo die Objekte zweier Relationen mittels eines geeigneten
Operators verglichen werden und Paare dieser Objekte als Ergebnis geliefert werden.
Als Beispiel stelle man sich in einer Relation Straßen, in einer anderen Flüsse vor. Eine
Anfrage, die alle Straßen liefern soll, die sich mit Flüssen kreuzen, muss zunächst einen
räumlichen Verbund der beiden Tabellen bilden. Dabei benutzt man einen Operator,
der überprüft, ob sich zwei Objekte überschneiden (intersection). Man erhält also alle
Straßen, deren Verlauf von dem der Flüsse geschnitten wird.
Um nicht alle Objekte der einen Relation mit allen Objekten der anderen Relation
vergleichen zu müssen (nested loops join), ist es hilfreich die Daten vorher zu partitionieren. Wenn es gelingt, Objekte, die räumlich nahe beieinander liegen, zu gruppieren,
können während des Join-Prozesses große Datenmengen schon ausgeschlossen werden, da
sie sich nicht in räumlicher Nähe des gerade betrachteten Objektes befinden.
Da die Anwendung des Vergleichs-Operators auf die konkreten Objekte der Datensätze
vergleichsweise rechenintensiv sein kann, unterteilt man die Verarbeitung der Verbundberechnung üblicherweise in zwei Stufen: In einer ersten Filterstufe wird mit Hilfe der
zu den Relationen gehörenden Index-Daten eine Kandidaten-Liste erstellt, die Objektpaare enthält, welche als Verbundpaar in Betracht gezogen werden müssen. Da in den
Index-Daten meistens nicht die tatsächliche Geometrie eines Objektes, sondern nur eine
Approximation davon aufgenommen ist, kann diese Filterstufe den Verbund nicht komplett berechnen, sondern nur dazu beitragen, bestimmte Kombinationen auszuschließen.
Die zweite Filterstufe verwendet dann diese Kandidatenliste, um die Verbund-Operation
anhand der tatsächlichen Datenobjekte der Kandidaten durchzuführen.
Ziel dieser Arbeit ist es, eine Möglichkeit zu finden, das objektrelationale Datenbankmanagementsystem Oracle 9i um die Berechnung räumlicher Verbunde auf Basis
benutzerdefinierter Indexstrukturen zu erweitern. Dazu wird eine im Rahmen einer anderen Diplomarbeit entwickelte Indexunterstützung verwendet, die die Datenbank um
benutzerdefinierte Indexe in der Form verallgemeinerter Suchbäume erweitert.
2
Auf diese Indexerweiterung (OraGiST) aufbauend, wird daher eine Bibliothek JoinGiST entwickelt, die es erlaubt, eine Verbundberechnung mittels zweier in verallgemeinerten Suchbäumen gespeicherten Indexstrukturen auszuführen.
Gliederung der Arbeit
Kapitel 2 beschreibt zunächst, was unter einem Verbund zweier Tabellen zu verstehen
ist. Da hier die Indexunterstützung bei einem Verbund von besonderem Interesse ist,
werden dazu einige der in Datenbanken verwendeten Indexierungsstrategien vorgestellt
und erläutert, wie diese bei der Berechnung eines Verbundes hilfreich sein können.
Speziell die Verbundalgorithmen mit den zugehörigen Indexierungsstrategien für räumliche Daten werden in Kapitel 3 betrachtet.
Kapitel 4 beschäftigt sich mit verallgemeinerten Suchbäumen, die als universelle Baumarchitektur eine Vielzahl verschiedener zur Verwendung als Index geeigneter Baumtypen
unterstützt.
Das folgende Kapitel betrachtet die Verwendung dieser Bäume als benutzerdefinierte
Indexstrukturen in Verbindung mit der Oracle-Datenbank. Die vorgestellte Bibliothek
OraGiST dient dabei als Bindeglied zwischen einer C++ -Implementierung verallgemeinerter Suchbäume und der Oracle-Datenbank. Zudem werden einige Schnittstellen der
Datenbank betrachtet, die im Zusammenhang mit dieser Arbeit oder den benutzerdefinierten Indexstrukturen von Bedeutung sind.
Im sechsten Kapitel wird schließlich der Algorithmus vorgestellt, der in dieser Arbeit
verwendet werden soll, um zwei verallgemeinerte Suchbäume miteinander zu verbinden.
Die darauf aufbauende Bibliothek JoinGiST zur Verbundberechnung zweier OraGiSTObjekte wird in Kapitel 7 vorgestellt.
Das letzte Kapitel betrachtet die Anwendung dieser Bibliothek mit einigen Beispieldaten und betrachtet das Abschneiden des Verbundalgorithmus bei der tatsächlichen
Berechnung darauf aufbauender Verbunde.
Wie die dazu benötigten OraGiST-Spezialisierungen angelegt werden, wird dazu nochmal kurz im Anhang A skizziert. Anhang B beinhaltet das dazugehörige Beispiel zur
Erstellung einer Erweiterung zu JoinGiST, um zwei Bäume dieses Typs zu verbinden.
Kapitel 2
Verbunde in Datenbanken
Wesentliches Ziel beim Einsatz moderner relationaler und objektrelationer Datenbanken
ist, die Speicherung redundanter Daten zu vermeiden oder zumindest zu kontrollieren,
soweit dies zur Sicherstellung des Erhalts der Datensicherheit oder zur PerformanceSteigerung notwendig ist. Dazu wird die Möglichkeit genutzt, Daten auf mehrere Tabellen
zu verteilen, so dass gleiche Informationen nicht für jeden Datensatz erneut gespeichert
werden müssen, sondern nur einmalig in den entsprechenden Tabellen abgelegt werden.
Die Verbindung zwischen den Informationen wird ebenfalls über Tabellen gespeicherte
Relationen hergestellt (dabei kann es sich auch um eine weitere Spalte in einer der Datentabellen handeln).
Eine Aufgabe des Datenbankmanagementsystems ist es, den berechtigten Benutzern
den Zugriff auf die so verteilten Daten zu ermöglichen. Dazu ist es notwendig, für eine
Anfrage an die Datenbank die entsprechenden Einträge in den betroffenen Tabellen zu
lokalisieren und zur Ausgabe oder weiteren Verarbeitung zusammenzufügen.
In der Datenbank einer Firma können beispielsweise in einer Tabelle Departments
alle Informationen zu einer Abteilung und in der Tabelle Employees die Informationen
über die Angestellten gespeichert sein, insbesondere auch die Abteilungsnummer (deptnr ) der Abteilung, der ein Angestellter zugeteilt ist. Ein Personalbearbeiter kann dann
folgende SQL-Anfrage verwenden, um die Namen aller Angestellter mit den zugehörigen
Abteilungsnamen zu erhalten:
select EMPLOYEES.name, DEPARTMENTS.name from EMPLOYEES, DEPARTMENTS
where EMPLOYEES.deptnr = DEPARTMENTS.deptnr;
In der Relationenalgebra entspricht dies:
πe.name, d.name (EMPLOYEES e ./ DEPARTMENTS d)
e.deptnr=d.deptnr
Eine solche Anfrage stellt die Datenbank vor die Aufgabe, zu allen Datensätzen (Tupeln) in Employees diejenigen in Departments zu finden, deren Einträge in den jeweiligen
deptnr -Spalten gleich sind. Da bei dieser Anfrage die Inhalte mehrerer Tabellen verknüpft
werden müssen, spricht man von einem Verbund (engl.: join).
KAPITEL 2. VERBUNDE IN DATENBANKEN
4
Hier ist der Operator, der zum Vergleich beider der beiden Tabellen herangezogen
wird, der Gleichheitsoperator (EMPLOYEES.deptnr = DEPARTMENTS.deptnr ). Aus
diesem Grund kann man auch von einem Equiverbund sprechen. Es sind aber auch andere
Verbundoperatoren möglich.
Wie ein Datenbanksystem eine Verbundanfrage bearbeiten kann, möchte ich in den
folgenden Abschnitten kurz skizzieren, wobei sich die Beschreibung an [HR01] und [Li97]
orientiert.
2.1
Verbund ohne Index
Die Bearbeitung der an die Datenbank gestellten Anfrage ist möglich, indem zu jeder Spalte der Tabelle Employees die Departments-Tabelle jeweils komplett durchsucht (gescannt)
wird, wobei man diejenigen Paare, bei denen die Vergleichsoperation erfüllt ist, hier also
gleiche deptnr, der Ergebnismenge zufügt. Dieses Verfahren, alle Datensätze einer Tabelle
für jeden Datensatz einer anderen Tabelle zu überprüfen, nennt man direkter Verbund
(nested loops join), wobei in einer äußeren Schleife (loop) alle Tupel der einen Tabelle
gelesen werden, um sie dann in einer inneren, im Schleifenrumpf der äußeren Schleife
befindlichen (nested ) Schleife, mit den jede Runde neu zu lesenden Tupeln der anderen
Tabelle zu vergleichen. Handelt es sich um größere Tabellen, so ist dieses Verfahren ineffizient, denn die Anzahl der zu lesenden Einträge entspricht in etwa dem Produkt der
Tabellenmächtigkeit der beteiligten Tabellen.
Die Verarbeitungsgeschwindigkeit bei der Ausführung eines Gleichheits-Verbundes,
lässt sich steigern, wenn die Daten linear angeordnet werden können und entsprechend
der Ordnung sortiert gespeichert wurden. Gibt es in wenigstens einer Tabelle keine Duplikate in der betreffenden, sortierten Spalte, so ist ein Verbund durch Mischen (merge
sort) möglich. Dabei werden die beiden Tabellen sequenziell durchlaufen, wobei jeweils
die Sequenz mit dem kleineren Element weiterrückt. Die gefundenen Paare werden der
Ergebnismenge zugefügt. Beim Mischverbund braucht jedes Tupel nur einmalig gelesen
werden, weswegen die Anzahl der Lesevorgänge proportional der Summe der Tabellenmächtigkeiten ist. Für nicht duplikatfreie, sortierte Tabellen bildet man jeweils Gruppen
mit gleichen Attributen, die dann beim Verbund jeweils miteinander verglichen werden.
1
2
1
1
1
1
1
1
2
2
2
3
2
3
4
5
5
5
4
5
5
5
Abbildung 2.1: Verbund zweier sortierter Tabellen
KAPITEL 2. VERBUNDE IN DATENBANKEN
5
Zur Illustration der Vergleichspartner betrachte man Abbildung 2.1, wo jeweils das
erste Attribut der linken Tabelle auf Gleichheit mit dem zweiten Attribut der rechten
Tabelle geprüft werden soll. Der linke Verbund besitze dabei keine Duplikate beim ersten
Attribut, während beim rechten Verbund erst die grau unterlegten Gruppen gebildet
werden, um deren Elemente anschließend miteinander zu vergleichen.
Da eine Tabelle in der Regel nur nach einer Spalte sortiert werden kann, ist ein vorheriges Umsortieren nötig, bevor ein Mischverbund erstellt werden kann. Das Umsortieren
nimmt dann aber bei größeren Tabellen, im Vergleich zum eigentlichen Verbund, die meiste Zeit in Anspruch. (Bei einer Tabellenmächtigkeit von N ist der Zeitbedarf O(N log N ).)
Um Tabellen nicht vor jedem Verbund neu sortieren zu müssen, sind weitere Strukturen
nötig, um einen Verbund effizient zu unterstützen. Dies ist mit einem Index möglich, einer Struktur die bereits zur Unterstützung der Suche in einzelnen Tabellen Anwendung
findet.
2.2
Indexe in Datenbanken
Sollen in einer Tabelle nicht alle, sondern nur einzelne Datensätze lokalisiert werden,
so kann die Datenbank durch Erstellung von Indexstrukturen unterstützt werden. Diese
werden für die Spalten erstellt, afür die eine Selektion stattfinden soll, ein Index erstellt
wird. Um bestimmte Einträge zu finden, ist dadurch kein kompletter Scan einer Tabelle
mehr notwendig. Statt dessen kann die Datenbank bei der Auswahl eines Zugriffspfades
entscheiden, einen Index zu verwenden.
In einem Index sind zu Schlüssel, die aus den Werten in der indexierten Spalte generiert werden, zumeist Verweise auf die Speicherorte der entsprechenden Daten abgelegt
(z.B. als Tupel-ID oder RowID). Bei einer Selektion wird daher in einem deutlich weniger Speicherseiten belegendem Index nachgesehen, welche Tupel als Ergebnis in Frage
kommen. Speicherzugriffe auf externen Speicher sind vergleichsweise zeitraubend. Somit
lohnt sich der zusätzliche Verwaltungsaufwand mit einer solchen Zugriffsstruktur besonders, wenn häufig Anfragen gestellt werden, die nur einen kleinen Teil des Datenbestandes
einer Tabelle selektieren. Dadurch braucht zusätzlich zu den Indexdaten möglicherweise
nur ein Bruchteil des eigentlichen Datenbestandes geladen werden.
Da Datenbanken die Tupel üblicherweise zu Seiten gruppiert im externen Speicher ablegen, sollte die Ergebnismenge des Index-Scans vor dem eigentlichen Datenzugriff nach
den Speicherseiten der referenzierten Speicherseiten sortiert werden. Sonst kann ein kompletter Scan der gesamten Tabelle schon bei mittlerer Selektivität einer Anfrage effizienter
sein als ein Indexscan, da der mögliche Geschwindigkeitsvorteil des indexgestützten Zugriffes durch die zur Auffindung der entsprechenden Seiten auf externen Speichermedien
benötigte Zeit bei wahlfreiem Zugriff zunichte gemacht wird, wenn beim einzelnen Aufsuchen der Tupel die Speicherseiten mehrfach gelesen werden müssen.
Statt Referenzen auf die Datensätze im Index abzulegen, ist es auch denkbar, weitere Kopien der Attribute abzuspeichern. Solche Indexe haben Vorteile bei aggregierenden
Funktionen (wie sum(GEHALT)), da die betreffenden Daten nicht erst in den Speicherseiten der Datensätze gesucht werden müssen, sondern direkt mittels des Indexes ausge-
KAPITEL 2. VERBUNDE IN DATENBANKEN
6
wertet werden können.
Bei den Zugriffstrukturen unterscheidet man, ob sie für die Indexierung von Primärschlüsseln oder Sekundärschlüsseln ausgelegt sind. Bei Primärschlüsseln ist der Suchschlüssel einmalig, so dass eine Suche auf höchstens einen Satz führt. Zugriffspfade für
Sekundärschlüssel, auch sekundäre Zugriffspfade genannt, können dagegen mehrere Datensätze als Ergebnis liefern. Die bei sekundären Zugriffspfaden verwendeten Strukturen
kann man in Einstiegsstruktur und Verknüpfungsstruktur aufteilen. Als Einstiegsstruktur sind alle Strukturen möglich, die auch bei Primärschlüsseln verwendet werden. Statt
zum Schlüssel eine RowID abzuspeichern, wird dann aber die Verknüpfungsstruktur oder
eine Referenz darauf im Index abgelegt. Typischerweise verwendet man als Verknüpfungsstruktur eine Liste von RowIDs. Statt einer einzelnen Referenz auf einen Tupel erhält man
bei einer erfolgreichen Suche diese Liste und damit gleich alle Referenzen auf Tupel, die
im Index den gleichen Schlüssel besitzen. Ein Schlüssel wird dabei nur einmal im Index
abgelegt, kommen ein weiterer Eintrag mit gleichem Schlüssel hinzu, wird lediglich die
Verknüpfungsstruktur um ein Element erweitert.
Alternativ wäre es auch möglich, die Einträge mehrfach mit gleichem Schlüssel im
Index abzulegen, wenn man dies bei der Suche entsprechend berücksichtigt. Dadurch
werden die Schlüssel zwar redundant gespeichert, man spart sich aber ein aufwendiges
Listenmanagement für die Verknüpfungsstruktur, weswegen dieses Verfahren in der folgenden Vorstellung einiger Indexstrukturen gelegentlich verwendet wird.
Als Indexstrukturen kommen vor allem die sogenannten Mehrwegbäume (und dabei
besonders B*-Bäume) in Frage, die in einem Knoten mehrere Verzweigungsmöglichkeiten besitzen. Binäre Suchbäume werden in Datenbanken selten eingesetzt, da sie überlicherweise auf Anwendungen, die im Hauptspeicher ablaufen, ausgerichtet, aber nicht
auf seitenbasierte Verarbeitung ausgelegt sind. Für einige Anwendungsfälle können HashVerfahren und Bitmap-Listen eingesetzt werden.
2.2.1
B*-Bäume
B*-Bäume gehören zu den hohlen“ oder blattorientierten Bäumen, denn die eigentlichen
”
Informationen befinden sich ausschließlich in den Blattknoten. Die Knoten haben feste
Größen, die sich üblicherweise an den Blockgrößen eines Speichertransfers zu einem externen Speichermedium orientieren (also z.B. 4kB). Die inneren Knoten beinhalten lediglich
Referenzschlüssel, die als Wegweiser bei der Suche nach den richtigen Blättern verwendet
werden. Wesentliche Kriterien eines B*-Baumes sind:
• Alle Blätter sind gleich weit von der Wurzel entfernt
• Interne Knoten beinhalten zwischen k und 2k Schlüssel
• Blätter haben zwischen j und 2j Einträge
• Die Wurzel nimmt eine Sonderstellung ein: Sie hat mindestens 2 Nachfolger oder
ist ein Blatt. Als Blatt kann sie auch weniger als j Einträge besitzen.
KAPITEL 2. VERBUNDE IN DATENBANKEN
7
Die Parameter k und j richten sich nach dem Speicherbedarf der in den Knoten gespeicherten Informationen und sagen im Wesentlichen aus, dass ein Knoten höchstens voll
und mindestens halbvoll sein muss.
Es ergeben sich zwei verschiedene Knotenformate: Interne Knoten enthalten Schlüssel
und Zeiger auf Nachfolgeseiten, Blätter Schlüssel Si und die dazugehörenden Datenelemente Di (Zeiger oder Zeigerlisten auf Datensätze). Die Informationen aller Knoten werden nach den Schlüsseln sortiert abgespeichert. Zur Suche nach Schlüsselbereichen (und
zur Restrukturierung des Baumes) ist es hilfreich, die Knoten nicht nur von der Wurzel
zu den Blättern zu verlinken, sonden zusätzliche Zeiger auf den linken und rechten Nachbarknoten vorzusehen. In Abbildung 2.2 sind die beiden Knotentypen dargestellt. Dabei
muss die aktuelle Anzahl der in internen Blättern gespeicherten Schlüssel x zwischen k
und 2k liegen (für Blätter: j ≤ y ≤ 2j). Man beachte auch, dass die internen Knoten auf
einen Nachfolgeknoten mehr verweisen, als Schlüssel darin gespeichert sind.
interne Knoten
Blattknoten
S1
S2
..........
Sx−1
Sx
freier Platz
S1 D1 S2 D2 .......... Sy−1 Dy−1 Sy Dy freier Platz
Abbildung 2.2: Möglicher Knotenaufbau eines B*-Baumes
Aus den eingeschränkten Verzweigungsgraden (j, k) der beiden Knotentypen des Baumes resultiert, dass sich die Baumhöhe nur in gewissen Grenzen bewegen kann. Für N
N
Datenelement bewegt sich die Baumhöhe h für h ≥ 2 zwischen 1 + log2k+1 ( 2j
) (alle KnoN
ten maximal gefüllt) und 2 + logk+1 ( 2j ) (minimal gefüllte Knoten, die Wurzel hat nur 2
Nachfolger).
Die Baumhöhe entspricht aber gerade der Anzahl der zu lesenden Seiten bei einer
Suche nach einem einzelnen Schlüssel. Damit lässt sich der Zeitaufwand zur Suche eines Schlüssels abschätzen. Zur Optimierung der Suche ist die Reduzierung der Höhe am
geeignetsten, denn dies ist der dominierende Faktor bei der Zugriffszeit. Grundgedanke
ist dabei die Verbreiterung des Baumes, was durch Erhöhung der Anzahl der in internen
Knoten gespeicherten Zeiger möglich ist. Dies kann bei gleicher Seitengröße geschehen,
indem die Schlüssellänge verkürzt wird. Bei gewissen Datentypen (z.B. Zeichenketten)
kann dies sehr leicht durch Kompressionsverfahren geschehen, da die internen Schlüssel
nur Wegweiserfunktion haben. (Bei Strings beispielsweise: Speicherung nur des Präfixs
oder Speicherung nur der Zeichen, in denen sich der Schlüssel vom Vorgänger und Nachfolger unterscheidet.)
Zur Suche im Baum vergleicht man den Suchschlüssel mit den in internen Knoten gespeicherten Referenzschlüsseln, bis man den ersten größeren oder gleichen gefunden hat.
Die Suche wird dann mit dem Teilbaum, der durch den links neben dem Referenzschlüssel liegenden Zeiger verlinkt ist, fortgesetzt, bzw. mit dem Zeiger ganz rechts, falls alle
Referenzschlüssel kleiner sind. Erreicht man die Blattebene, so sucht man, bis man den
passenden Schlüssel gefunden hat.
KAPITEL 2. VERBUNDE IN DATENBANKEN
8
Da die Einträge auf Blattebene ebenfalls sortiert vorliegen, hat man alle Einträge
gefunden, sobald ein größerer Schlüssel als der Suchschlüssel beim sequentiellen Durchsuchen der Schlüssel auftritt. Passiert dies nicht, so wird die Suche in den rechten Nachbarknoten fortgesetzt. Zeiger auf die Nachbarknoten erleichtern dies. Im B*-Baum ist nicht
nur eine Suche auf Gleichheit möglich, sondern auch auf einen Wertebereich sehr einfach.
Die Suche beginnt mit der linken Intervallgrenze als Suchschlüssel. Auf der Blattebene
werden dann alle Einträge bis zur rechten Grenze geliefert. Soll die Sortierreihenfolge
umgedreht werden, so nimmt man die obere Intervallgrenze, wobei man evtl. den rechts
neben den Referenzschlüsseln liegenden Zeiger verfolgt. Auf der Blattebene wird dann der
Verweis auf den linken Nachbarknoten ausgenutzt, und ab dort jeweils von rechts nach
links bis zur unteren Intervallgrenze gesucht.
Die Einfüge- oder Löschoperationen funktionieren sehr einfach, solange dadurch die
Einschränkungen der Knotenbelegung nicht verletzt werden. (An der richtigen Position einfügen, bzw. löschen und die sonstigen Einträge entsprechend aufrücken.) Im Falle
einer Unter- oder Überfüllung werden Algorithmen zur dynamischen Restrukturierung
eingesetzt. Dazu wird ein voller Knoten entweder auf die Nachbarknoten verteilt (die mit
Zeigern auf die Nachbarknoten der gleichen Ebene leicht zu finden sind) oder man spaltet
einen Knoten in zwei neue, halb so große Knoten auf. Der linke Knoten wird anstelle des
ursprünglichen Knotens im Vorgängerknoten verlinkt (der Referenzschlüssel links daneben muss evtl. geändert werden), der rechte muss rechts daneben mit einem neuen Zeiger
und entsprechendem Referenzschlüssel in den Vorgängerknoten eingesetzt werden. Die
Referenzschlüssel, die immer zwischen zwei Zeigern und damit Teilbäumen stehen, müssen immer genau so gewählt werden, dass alle Blätter im linken Teilbaum kleiner-gleich
und im rechten größer-gleich sind. Sie können damit aus dem linkesten Blatt des rechten
Teilbaumes generiert werden. Das Aufsplitten kann sich bis zur Wurzel fortsetzen, falls
keine Einträge auf Nachbarknoten verteilt werden können. Wird die Wurzel aufgeteilt, so
erhält der Baum eine neue Wurzel mit den beiden beim Aufteilen enstandenen Knoten
als Nachfolger.
Bei einer Unterfüllung kann man versuchen, sich zunächst Einträge aus Nachbarknoten
zu leihen, ansonsten müssen zwei Knoten zusammengefasst werden. Dies löst wiederum
ein Entfernen von Referenzschlüssel und Zeigern aus den Vorgängerknoten aus, was sich
bis zur Wurzel forsetzen kann. Wurzeln mit nur noch einem Nachfolger werden gelöscht,
und der alte Nachfolger als neue Wurzel verwendet.
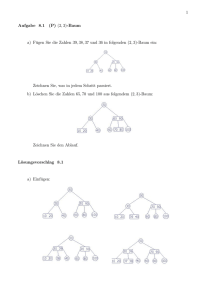
Abschließend betrachte man noch als Beispiel den B*-Baum in Abbildung 2.3, wo ein
Element mit Schlüssel p“ eingesetzt werden soll. Zur Vereinfachung ist in den Blättern
”
nur die Schlüsselkomponente dargestellt und die Blätter fassen lediglich einen Eintrag.
Die internen Knoten haben bei zwei Referenzschlüsseln Platz für 3 Nachfolgeknoten.
Zuerst wird der Knoten gesucht, in den p eingesetzt werden muss. Dies ist das Blatt
1 (auf der vorletzten Ebene ist im Knoten 2 der Schlüssel q“ der erste größer-gleich p“,
”
”
der linke Zeiger führt zu 1). Das Blatt fasst (hier) nur einen Eintrag, deswegen wird es
geteilt und das Blatt mit p“ erzeugt. Der linke Knoten ist Blatt 1a, er bleibt in 2 verlinkt.
”
Das neue Blatt 1b muss rechts von o“ eingefügt werden, mit Schlüssel p“. In 2 ist nicht
”
”
genug Platz für einen neuen Eintrag, deswegen muss wieder geteilt werden. Die Knoten
KAPITEL 2. VERBUNDE IN DATENBANKEN
9
j t
3
e
4
n r
x
2
c c
f
a c c
l m
o q
r s
j l m 1
r r s
e f
n o q
v
y z
x y z
t v
j r
n p
e
t x
2a
c c
f
a c c
l m
2b
q
o
j l m
e f
r s
v
r r s
n o
p q
y z
x y z
t v
1a 1b
Abbildung 2.3: Aufteilung von Knoten beim Einsetzen in einen B*-Baum
2a und 2b entstehen und müssen in 3 eingetragen werden. Eigentlich müsste Knoten 3
geteilt werden, da aber in Knoten 4 noch Platz ist, kann ein Eintrag verschoben werden.
Dies bewirkt auch, dass der Referenzschlüssel r“ in die Wurzel wandert, und t“ als neuer
”
”
Schlüssel in Knoten 4, denn r“ ist jetzt das linkeste Blatt des ganz rechten Teilbaumes
”
in der Wurzel. In 3 ist jetzt Platz, um den Knoten 2b einzutragen, dessen linkestes Blatt
p“ ist.
”
2.2.2
Hash-Index
Hash-Indexe verwenden Schlüsseltransformations-Verfahren zur Auffindung der Indexinformationen. Die Speicheradresse des Indexeintrages eines Datensatzes wird durch eine
geeignete Hash-Funktion direkt aus dem Suchschlüssel berechnet. Im Idealfall wird keine weitere Hilfsstruktur benötigt, um dadurch den Datensatz aufzufinden. Die Aufgabe
der Hashfunktion besteht darin, allen möglichen Werten des Schlüsselraumes einen Wert
des Adressraumes zuzuweisen. Für die bei Datenbankanwendungen interessanten HashVerfahren, die auf Externspeicher auf Seitenbasis ausgelegt sind, entspricht der Adressraum einer Seitennummer, in der möglichst alle Indexeinträge mit demselben Hash-Wert
untergebracht werden.
Da üblicherweise nicht alle der möglichen Schlüssel gerade verwendet werden, ist es
in der Regel nicht möglich, eine Hashfunktion zu finden, die eine kollisionsfreie Satzzuordnung ermöglicht, ohne extreme Speicherplatzverschwendung in Kauf zu nehmen.
Deswegen nimmt man hin, dass zu verschiedenen Schlüsseln die gleiche Adresse berech-
KAPITEL 2. VERBUNDE IN DATENBANKEN
10
net wird. Diese Speicher- oder Segment-Adresse bezeichnet eine Seite fester Größe des
externen Speichers, auch Bucket (Eimer, Korb) genannt, in dem mehrere Datenelemente
Platz finden können, ohne eine Kollision auszulösen.
Zahlreiche Hash-Verfahren wurden im Laufe der Zeit entwickelt, die eine gleichmäßige
Ausnutzung des zur Verfügung stehenden Adressbereiches erstreben. Einige davon sind:
Restklassenbildung: (Divisionsrestverfahren) Die Speicherdarstellung des Schlüssels
wird als ganze Zahl s interpretiert. Mit einer Hash-Funktion h(s) = s mod n
wird daraus eine Restklasse berechnet, die eine Speicheradresse des Adressraumes
der Mächtigkeit n ergibt. Mit der Wahl der Bucket-Anzahl wird dabei wesentlich
die Gleichverteilung der Schlüssel beeinflusst. Empfehlenswert sind Primzahlen, die
nicht benachbart zu Potenzen des vom Rechner verwendeten Zahlensystems liegen
sollten, da sich sonst bei gleichen Endziffern ähnliche Adressmengen in verschiedenen Zahlenbereichen wiederholen.
Dieses Verfahren wird insbesondere bei nicht bekannter Schlüsselverteilung empfohlen.
Faltung: Der in einzelne Bestandteile zerlegte Schlüssel wird durch Spiegelungen oder
Verschiebeoperationen überlappend übereinandergelegt. Durch Addition, Multiplikation oder Boolsche Verknüpfung erhält man einen Hash-Wert, der nur noch an
den verfügbaren Adressraum angepasst werden muss.
Dieses Verfahren kann gut in Kombination mit der Restklassenbildung eingesetzt
werden, um eine noch bessere Gleichverteilung zu erreichen.
Multiplikationsverfahren: Der Schlüssel wird mit einer Konstanten multipliziert oder
mit potenziert. Aus der sich ergebenden Zahl wählt man eine von der Größe des
Adressraumes abhängige Anzahl von Bits aus, die dann den Hash-Wert, also die
Adresse bilden.
Zufallsgenerator: Ein an den zur Verfügung stehenden Adressraum angepasster PseudoZufallszahlengenerator wird mit dem Schlüssel als Saat“ aufgerufen. Sollte eine
”
Kollisionsbehandlung notwendig sein, so kann mit einem weiteren Aufruf des Generators (reproduzierbar) eine ganze Folge von weiteren Adressen berechnet werden.
Ziffernanalyse: Ist die Menge der zu speichernden Schlüssel vorab bekannt, so kann
diese Menge untersucht werden, um eine Verteilungsschiefe bei ungünstiger Parameterwahl (z.B. der zu verwendenden Bits) rechtzeitig zu erkennen und zu beheben.
Dieses Verfahren ist sehr aufwendig, gewährleistet aber eine gute Gleichverteilung.
Leider sind in produktiven Umgebungen die Schlüssel üblicherweise nicht a priori bekannt, weswegen das Verfahren praktisch nur für statische Daten angewendet
werden kann.
Da es bei festgelegter Anzahl von Adressen im Laufe des Datenbankbetriebes zu Kollisionen, also vollen Index-Speicherseiten, kommen kann, ist eine Kollisions- oder Überlaufbehandlung notwendig, wenn weitere Schlüssel indexiert werden sollen. Bei der Suche
im Index sind evtl. vorhandene Überlaufbereiche entsprechend mit einzubeziehen.
KAPITEL 2. VERBUNDE IN DATENBANKEN
11
Tritt eine Kollision auf, so kann diese aufgelöst werden, indem ein Speicherplatz innerhalb einer anderen Seite des ursprünglich Adressraumes (des Primärbereiches) gesucht
wird oder es wird eine weitere Speicherseite im sogenannten Überlaufbereich erstellt.
Möchte man nur den Primärbereich verwenden, so ist die Aufnahmefähigkeit des Indexes
durch die bei der Indexerstellung vorgegebene Seitenzahl begrenzt. Gibt es ein Kollision,
so verwendet man den Korb mit der nächsten relativen Seitennummer, erstellt eine Verkettung der Seiten oder benutzt eine weitere Hash-Funktion (oder einen weiteren Aufruf
der Hash-Funktion) zur Berechnung des Ablageplatzes. Durch Clusterbildung kann es bei
hohem Belegungsfaktor (≥ 80%) verstärkt zu Mehrfachkollisionen kommen. Zusätzlich
ist das Löschen erschwert, da die Kollisionen dann wieder aufgelöst werden müssen, bzw.
man Löschvermerke und spätere Reorganisation benötigt. Daher empfiehlt es sich einen
separaten Überlaufbereich einzurichten. Dort können neue Speicherseiten angelegt werden, die durch Verkettung mit dem Primärbereich erreichbar sind. Dadurch erhöht sich die
Anzahl der zu einem Hash-Wert speicherbaren Einträge dynamisch, jeweils um die Größe
eines Korbes. Auch wenn die doppelte Kapazität des Primärbereiches gespeichert werden
muss, kann die Anzahl der durchschnittlich benötigten Seitenzugriffe üblicherweise < 2
gehalten werden.
Als Beispiel für einen Hash-Index mit verkettetem Überlaufbereich betrachte man
Abbildung 2.4, wo die Hashfunktion aus einer Faltung mit anschließendem Divisionsrestverfahren besteht.
Ein Datenelement, dessen zugehöriger Schlüssel binär die Folge 1001011010101100
besitzt, soll neu in den Index aufgenommen werden. Dazu wird der Schlüssel in ein höherwertiges und niederwertiges Byte aufgeteilt, und die beiden Teile mit einer bitweisen
XOR-Operation (⊕) verknüpft. Die sich ergebende Zahl hat dezimal den Wert 58. Da
fünf Buckets vorgesehen sind, wird mit dem Divisionsrestverfahren eine Korb-Nummer
berechnet, wobei als Modul 5 verwendet wird. Der berechnete Bucket (3) ist schon voll,
so dass in den Überlaufbereich ausgewichen werden muss. Dieser ist über Verkettung
der zusätzlich benötigten Seiten an den Primärbereich angeschlossen. Dort ist noch für
zwei Elemente Platz, so dass ein Eintrag ohne weitere Kollision an der dritten Position
vorgenommen werden kann.
Ist die Indexgröße bekannt, so kann mit einem Verfahren, das nach dem Prinzip des
Open Adressing arbeitet, ein Index erstellt werden, der mit genau einem Externspeichzugriff einen gesuchten Indexeintrag findet. Die Belegung sollte dabei aber dennoch nicht
über etwa 80% steigen, denn sonst kann die Zugriffseigenschaft nicht mehr garantiert
werden. Als zusätzliche Datenstruktur wird eine sogenannte Separatortabelle ständig im
Hauptspeicher gehalten, die etwa ein Byte pro Bucket benötigt.
Zunächst erfolgt die Beschreibung der Suche: Zu jedem Schlüssel wird nicht nur ein
Hash-Wert, sondern gleich ein ganzer Vektor von möglichen Adressen berechnet, z.B. mit
einem Pseudozufallsgenerator, der den Schlüssel als Saat verwendet. Zusätzlich wird mit
einer weiteren Funktion eine Signatur für jeden Schlüssel berechnet. Die Separatortabelle
enthält für jeden Bucket einen Eintrag, der bestimmt, bis zu welcher Signatur Einträge auf
der entsprechenden Speicherseite gemacht werden. Zur Bestimmung der Speicherseite auf
dem externen Speicher werden die Werte des Hash-Vektors nacheinander durchgegangen
KAPITEL 2. VERBUNDE IN DATENBANKEN
Primärbereich
0 S1
D1
D2
D3
1 S1
D1
D2
D3
D4
2 S1
D1
D2
D3
D4
S2
S3
S2
S3
S4
S2
S3
S4
3 S1
S2
S3
S4
4 S1
S2
D1
D2
D3
D4
12
Überlaufbereich
S1
S2
S3
S4
D1
D2
D3
D4
S1
D1
Schlüssel: 1001011010101100
10010110
00111010
S1
S2
S3
D1
D2
D3
001110102 = 5810 mod 5
3
D1
D2
Abbildung 2.4: Hash-Index mit separatem Überlauf und verketteten Buckets
(sondiert), wobei jeweils der Eintrag in der Separatortabelle mit der Signatur verglichen
wird. Ist die Signatur kleiner als der Eintrag in der Tabelle, so befindet sich der Datensatz
in dem entsprechenden Bucket (oder existiert nicht), ansonsten muss der Eintrag des
nächsten Vektor-Elements überprüft werden.
Soll ein neuer Eintrag eingefügt werden, so wird ebenfalls ein Hash-Vektor und eine
Signatur für den zugehörigen Schlüssel berechnet. Wie bei der Suche wird die Signatur
entsprechend dem Hash-Vektor mit den in Frage kommenden Buckets bzw. ihren Einträgen in der Separatortabelle verglichen. Der erste Bucket, wo die Signatur kleiner als der
Eintrag in der Separatortabelle ist, kommt damit in Frage. Ist dort noch genügend Platz,
so kann der Eintrag vorgenommen werden. Ist dies nicht der Fall, so wird der Eintrag des
Buckets in der Separatortabelle verkleinert, bis dadurch wenigstens ein Platz im Bucket
frei wird. (Bei leerer Tabelle und damit bis zum ersten Überlauf, steht der Eintrag in der
Separatortabelle auf dem maximalen Wert.) Dies bedeutet, dass diejenigen Einträge, die
durch den jetzt niedrigeren Separator-Eintrag nicht mehr in diesem Bucket bleiben dürfen
und entsprechend ihres Hash-Vektors in andere Körbe eingetragen werden müssen. Damit
sich dies nicht unendlich fortsetzt, ist es sehr wichtig, dass der Füllgrad des Indexes klein
genug bleibt (als Richtwert: < 80%), sonst explodieren“ die Einfügekosten. Da es beim
”
Löschen von Einträgen äußerst schwierig ist, die Einträge zu finden, die bereits den Korb
wechseln mussten, ist ein Erhöhen der Einträge in der Separatortabelle nicht vorgese-
KAPITEL 2. VERBUNDE IN DATENBANKEN
13
hen, denn ohne die Schlüssel ist auch der Hash-Vektor nicht bekannt Stattdessen müsste
der Index komplett neu aufgebaut werden, wenn die Einträge in der Separatortabelle zu
niedrig werden.
Die bisher beschriebenen Verfahren verwenden eine feste Anzahl Buckets, weswegen sie
zu den statischen Hash-Verfahren zählen. Daneben gibt es die dynamische Verfahren, bei
denen man versucht, die Bucket-Anzahl an den Speicherbedarf anzupassen. Dabei wird bei
einem Überlauf“ die Anzahl der Buckets so erhöht, dass weitere Einträge beim Einfügen
”
bereits durch die Hash-Funktion richtig aufgeteilt werden können. Ein Verfahren, dass
einen Index für die Buckets verwendet, möchte ich dazu kurz skizzieren:
Statt den Wert der Hash-Funktion, zum Beispiel durch das Restklassenverfahren,
an die vorgegebene Anzahl an Körben anzupassen, wird der dabei berechnete PseudoSchlüssel zunächst nicht weiter transformiert. Stattdessen wird damit ein Blatt eines
Digitalbaum gesucht, welches den entsprechenden Korb darstellt. Die Kanten des Digitaloder Radix-Baumes sind jeweils mit einem Teil (ein oder bei größerem Verzweigungsgrad
entsprechend mehrere Bits) der Schlüssel des Bit-Strings markiert, die im Blatt am Ende
des Weges durch den Baum zu finden sind. Droht beim Einsetzen ein Überlauf, so wird
der Baum an der entsprechenden Stelle weiter aufgeteilt. In Abbildung 2.5 kann man
beispielsweise sehen, wie dies beim Einsetzen des Schlüssels mit Hash-Wert 11010 gleich
zum mehrfachen Aufteilen des Buckets mit dem Präfix 1 führt. Es entstehen zunächst
Buckets, die die Pseudoschlüssel, die mit 10 und 11 beginnen, aufnehmen würden. Da es
aber keinen zu speichernden Hash-Wert gibt, der mit 10 beginnt, landen alle Einträge im
rechten Teilbaum. Dieser wird abermals aufgeteilt in zwei Körbe für die Pseudo-Schlüssel,
die mit 110 respektive 111 beginnen.
0
0
1
0
1
00010
00101
00110
00110
01000
01101
01100
01110
00*
01*
0
11001
11101
11111
11110
1*
1
1
0
1
0
00010
00101
00110
00110
01000
01101
01100
01110
00*
01*
1
10*
11001
11010
11101
11111
11110
110*
111*
Abbildung 2.5: Hash-Index mit Digitalbaum als Index
Zur leichteren Veranschaulichung sind in der Abbildung die Hash-Werte, d.h. Pseudoschlüssel, in den Blättern eingetragen. Tatsächlich würde man dort wie immer die
eigentlichen Schlüssel und zugehörigen Datenelemente abspeichern.
Das Löschen von Einträgen ist problemlos möglich. Gemeinsam an einem Knoten angehängte Blätter können dabei problemlos wieder zusammengefügt werden, falls dabei
KAPITEL 2. VERBUNDE IN DATENBANKEN
14
genügend freie Positionen entstehen. In Abbildung 2.5 reicht beispielsweise das Löschen
eines Eintrages in den Blättern mit Präfix 110 oder 111, um die Blätter wieder zusammenfügen zu können (dann auch gleich mit dem leeren Knoten). Problematisch ist, dass
der Baum nicht ausbalanciert wird. Wird er durch zu viele gleiche Pseudoschlüssel bis
zur vollen Länge der Bit-Strings erweitert, so muss eine andere Kollisionsbehandlung
verwendet werden.
Anzumerken ist noch, dass mit Hash-Indexen zwar Indexstrukturen realisierbar sind,
die mit nur einem externen Speicherzugriff auskommen können, um einen Indexeintrag
zu lokalisieren, aber im Allgemeinen geht dabei die Ordnung der Einträge verloren. Bereichsanfragen sind deshalb nicht ohne weiteres zu realisieren.
2.2.3
Bitmap-Listen
Bitmap-Listen oder Bitmap-Indexe sind besonders gut zur Indexierung von Attributen geeignet, die sehr viele gleiche Schlüssel besitzen. Die Idee besteht darin, zu jedem Schlüssel
einen Bit-String zu speichern. Die einzelnen Bitpositionen dieses Bit-Strings korrespondieren wiederum mit einzelnen Datensätzen (oder Speicherseiten, die qualifizierte Datensätze
enthalten). Problematisch bei der Indexierung einzelner Sätze in den Seiten ist, dass in
modernen Datenbanken die Satzlänge meist variabel ist (z.B. bei Zeichenketten). In den
Bitlisten müssen dann evtl. sehr viele ungenutzte Bits bereitgehalten werden, wenn lange
Einträge eine Seite füllen, also nicht die maximale Anzahl von Einträgen in der Seite ausgenutzt wird, oder die maximale Anzahl in einer Seite speicherbarer Einträge wird auf die
vorgesehene Anzahl Bitpositionen in der Bitliste begrenzt, was bei sehr vielen kleinen Einträge zu ungenutzten Speicherseiten führt. Ein Ausweg bietet die zusätzliche Einrichtung
einer Zuordnungstabelle, die auch bei bestimmten Satzaddressierungstechniken eingesetzt
wird. Eine Bitposition entspricht dann einem Eintrag in der Zuordnungstabelle, die zur
Bestimmung der Seite eines Datensatzes herangezogen wird.
Die Vorteile von Bitmap-Listen bestehen in geringerem Speicherplatzverbrauch, falls
nur wenige verschiedene Schlüssel vorhanden sind. Statt Zeiger auf jeden Datensatz (oder
jede Seite) in einem Mehrwegbaum zu speichern, die meist jeweils mehrere Byte beanspruchen, reicht hier ein einzelnes Bit, um einen Eintrag anzuzeigen.
Beispielsweise betrachte man Abbildung 2.6, wo die einzelnen Bit-Listen für die untereinander angeordneten Schlüssel eine Matrix ergeben. Im Beispiel soll der Index auf
Speicherseiten verweisen, daher können mehrere Schlüssel in einer Seite vorkommen (mehrere 1en in einer Spalte). In einer Spalte steht genau dann eine 1, wenn der zu der Zeile
gehörende Schlüssel in der entsprechenden Seite vorhanden ist. Schlüssel wie S2 , die auf
fast allen Seiten vorhanden sind, benötigen nur einen relativ kurzen Bit-String, statt über
20 Einträge in einem Mehrwegbaum bzw. der Verknüpfungsstruktur eines sekundären Zugriffspfades.
Sucht man Tupel, die im indexierten Attribut die Schlüssel S1 oder S2 besitzen, so ist
dies mit einer OR-Verknüpfung der Bit-Strings zu ermitteln, Sind mehrere Attribute einer
Relation mit einem Bitmap-Index indexiert, können auch Bit-Strings der verschiedenen
Indexe bei Anfragen wie
KAPITEL 2. VERBUNDE IN DATENBANKEN
15
111 111 1 1 1 12 2 22 222 222
01 23 456 789 012 345 678 901 23 456 789 Seiten−Nr.
S 1 00 00 100 000 000 000 110 0 01 00 001 000
S 2 11 11 100 111 010 101 110 111 11 101 010
S 3 00 11 011 000 101 000 000 011 11 000 101
S 4 01 10 000 100 000 010 000 000 00 010 100
S 5 10 01 101 000 000 101 011 010 11 100 001
S 6 00 00 000 010 000 000 000 000 00 000 000
Schlüssel
Abbildung 2.6: Bitmap-Index: Schlüssel mit Bit-Strings als Bitmatrix dargestellt
select * from JEANS
where COLOR = ’RED’ and SIZE = ’L’;
miteinander verknüpft werden. Eine effiziente Hardwareunterstützung ist dabei möglich,
denn mengenalgebraische Operationen (AND, OR, NOT) lassen sich in modernen Prozessoren
oft schon mit einer Wortlänge von 64 Bit oder mehr parallel verarbeiten: Die Bitlisten
können dadurch schnell stückweise miteinander verknüpft werden.
Negativ auf den Speicherplatzbedarf und damit auch auf die Performance wirken sich
viele Einträge aus, die nur auf wenigen (oder sogar nur einer) Seite vorhanden sind. Denn
im Prinzip speichert man in der Bit-Liste nicht nur die Anwesenheit eines Attributes
in einem Datensatz (Bit gesetzt), sondern mit einem ungesetzten Bit auch dessen Abwesenheit ab. Sollten in Abbildung 2.6 viele Schlüssel wie S6 vorkommen, so wäre ein
Mehrwegbaum möglicherweise die geeignetere Indexstruktur. Für Primärschlüssel ist ein
Bitmap-Index ungeeignet, da jeder Schlüssel nur genau einmal vorkommt.
Dem Speicherplatzbedarf bei zunehmender Anzahl von Schlüsseln kann man in gewissen Grenzen entgegentreten, wenn man die Bit-Strings durch den Einsatz von Komprimierungstechniken effizienter speichert. So bietet es sich an, lange Null- oder Eins-Folgen,
oder häufig vorkommende Bitmuster durch bestimmte Codes zu kodieren. In Frage kommen praktisch alle verlustlos komprimierenden Verfahren, wie Bitfolgen-Komprimierung
(run length compression), besondere Codes für Nullfolgen und Bitmuster, Huffman-Codes,
Block-Kompression mit einem zusätzlichen Dicrectory, etc.
2.2.4
Verallgemeinerte Zugriffspfadstruktur
Bisher wurden Verfahren beschrieben, wo sich die Indexierung auf genau ein Attribut
genau einer Tabelle bezog. Daher ist es naheliegend, für jeden Index eine eigene Datenstruktur (z.B. einen B*-Baum) aufzubauen, denn dabei werden die Daten üblicherweise
auch nahe beieinander auf dem externen Speicher abgelegt.
Einen etwas anderen Ansatz verfolgt man bei verallgemeinerten Zugriffspfadstrukturen. Die Idee besteht dabei darin, Schlüssel mit dem gleichen Wertebereich in einer
gemeinsamen Struktur zu verwalten, auch wenn sie von verschiedenen Attributen oder
KAPITEL 2. VERBUNDE IN DATENBANKEN
16
Tabellen stammen. So könnte man beispielsweise Längenangaben, Zeiten, und Personalnummern, möglicherweise nach einer geeigneten Konvertierung, als Ganzzahlen in einem
gemeinsamen Mehrwegbaum unterbringen. Verwendet man B*-Bäume, so bleiben die internen Knoten davon im Aufbau unberührt. Dort dienen die Referenz-Schlüssel schließlich
nur als Wegweiser zu den richtigen Blättern. Allerdings ändert sich der Aufbau der Blätter, wo zu jedem Schlüssel Informationen zu allen in diesem Baum indexierten Attributen gespeichert werden. Statt eines Datenelementes speichert man Längen-Informationen
und Zeigerlisten für die jeweiligen Teil-Indexe. In Abbildung 2.7 ist dies für ein SchlüsselDatenelement-Paar in einem B*-Baum skizziert.
L1 Zeiger
L2 Zeiger
Ln Zeiger
Schlüssel L1 L2 ... Ln Z11 ... Z1j Z21 ... Z2k ... Zn1
Längen−Informationen
Znl
n Zeigerlisten
Abbildung 2.7: mehrere Zeigerlisten bei verallgemeinerten Zugriffspfaden
In der Abbildung werden n Attribute in einem gemeinsamen Index verwaltet. Das
Datenelement zum Schlüssel besteht daher aus n Längenangaben und n Zeigerlisten. Die
Längenangaben Li ermöglichen das Auffinden der zugehörigen Zeigerlisten Zih . Für Primärschlüssel haben die Zeigerlisten entweder 0 oder 1 Element (Primärschlüssel existiert
nicht, oder existiert), andere Attribute können beliebig häufig vorkommen. Da sich durch
die Zeigerlisten variabler Länge nicht immer gleich viele Schlüssel und Datenelemente
in einem Knoten unterbringen lassen, ist eine geeignete Überlaufbehandlung vorzusehen. Dies kann über eine Verkettung weiterer zu einem Knoten gehörenden Seiten in
einem separaten Überlaufbereich (wie bei den Hash-Indexen) oder durch die Aufteilung
in weitere Blätter des Baumes, z.B. mit einem weiteren (gleichen) Schlüssel, erfolgen. Die
Baumoperationen müssen dies entsprechend berücksichtigen. So muss beispielsweise die
Suchfunktion fortfahren, bis alle dem Suchkriterium entsprechenden Schlüssel gefunden
wurden, nicht nur bis zum ersten.
Die Höhe eines B*-Baumes als verallgemeinerte Zugriffsstruktur ändert sich auf Grund
des hohen Verzweigungsgrades nur unwesentlich, denn der Verzweigungsgrad der internen
Knoten ist von den zusätzlich abzulegenden Informationen nicht betroffen. Es können
aber, im Vergleich zu einem einfachen Index, zusätzliche Schlüssel hinzukommen, da auch
mehr Blätter benötigt werden. Dies sollte den Baum aber lediglich um einige wenige
Ebenen vergrößern. Daher sind die direkten Zugriffe nur unwesentlich langsamer als bei
einfachen Indexstrukturen.
Durch die gemeinsame Nutzung der Schlüssel brauchen diese nicht mehrfach in internen Knoten verschiedener einfacher Indexe abgespeichert zu werden, zudem ist es sogar
wahrscheinlicher, dass sich (zumindest die oberen) Knoten bereits in datenbankinternen Puffern befinden, wenn ein neuer Indexzugriff erfolgt. Aufgrund der zusätzlichen
Informationen in den Blättern (evtl. mit Verkettung) ist ein sequentieller Zugriff auf die
Datensätze unter Zuhilfenahme des Indexes nur geringfügig langsamer.
KAPITEL 2. VERBUNDE IN DATENBANKEN
17
Besonders vorteilhaft ist dagegen, dass bestimmte Verbunde auf geradezu natürliche
Weise unterstützt werden: Beim eingangs erwähnten Beispiel
select EMPLOYEES.name, DEPARTMENTS.name from EMPLOYEES, DEPARTMENTS
where EMPLOYEES.deptnr = DEPARTMENTS.deptnr;
befinden sich bei gemeinsamer Indexierung die Informationen zu EMPLOYEES.deptnr
und DEPARTMENTS.deptnr beim gleichen, gemeinsamen Schlüssel, und können damit
direkt ausgegeben werden.
2.3
Indexgestützter Verbund
Existiert ein Index auf eine oder mehrere der bei einem Verbund beteiligten Spalten, so
kann dieser auch bei der Bearbeitung einer Verbundanfrage verwendet werden. Nicht mehr
alle Datensätze müssen bei der Suche nach Verbundpaaren (evtl. mehrfach) eingelesen
werden, sondern dies kann mit dem deutlich kleineren Index geschehen. Der Index passt
möglicherweise sogar komplett in den Hauptspeicher des Datenbankrechners, so dass dort
der komplette Verbund berechnet werden kann, bevor die zugehörigen Datensätze gelesen
werden müssen.
Lassen sich die Schlüssel des Indexes ordnen, so werden die Indexeinträge in der Regel
auch geordnet gespeichert, so dass sie im Index schnell gefunden werden. Dies kommt
wiederum den Verbundalgorithmen zugute, die geordnete Wertemengen benötigen. Zur
Anwendung des bereits erwähnten Mischverbundes reicht es bereits, wenn über den Index
die Tupel auf logischer Ebene geordnet sind. Statt der eigentlichen Tupel kann der Verbund anhand der Schlüssel der Indexeinträge stattfinden. Die Verarbeitung der Verbünde
kann ausschließlich mit Schlüssel- und RowID-Listen erfolgen, wenn für die betroffenen
Attribute geeignete Indexe zur Verfügung stehen. Ist kein Verbund kompletter Tabellen gefordert, so kann diese Liste noch mit weiteren Selektionen verknüpft werden (oder
bereits sein), bevor der eigentliche Zugriff auf die Datentupel erfolgen muss.
2.3.1
Verbundindexe
Als spezieller Zugriffspfad für Zwei-Weg-Verbunde ist es möglich, einen Verbundindex
(join index ) bereitzustellen. Prinzipiell handelt es sich dabei um einen vorberechneten
Verbund: Die Tupel-IDs (TIDs) der Verbundpaare bilden dabei einen Eintrag in einer
zweistelligen Relation V , die alle Paare eines Verbundes enthält, die zu einer gegebenen
Operation auf zwei Verbundattributen gehören. Also etwa
V = {(a.T ID, b.T ID)|f (a.α, b.β) = true, a ∈ A, b ∈ B}
wobei α und β die Verbund-Attribute der Zeilen a und b in den Relationen A, B sind.
Die Relationen müssen dabei nicht verschieden sein. Die boolsche Funktion f kann auch
deutlich komplexer als einfache Vergleiche (=, 6=, <, ≤, etc.) sein und bereits Selektionen
auf α und β berücksichtigen.
Da ein solcher Verbundindex nicht notwendigerweise im Hauptspeicher des Datenbanksystems Platz findet, sollte er geeignet gespeichert werden. Zum schnellen Zugriff
KAPITEL 2. VERBUNDE IN DATENBANKEN
18
empfiehlt sich eine geordnete Speicherung jeweils einer Kopie in zwei B*-Bäumen, eine
nach dem ersten, die andere nach dem zweiten Attribut sortiert. Sollte die Verbundrichtung vorgegeben sein, reicht möglicherweise auch die Speichung einer nach dem relevanten
Attribut sortierten Kopie.
A
T−ID1
B
T−ID7
T−ID3
T−ID2
T−ID1
T−ID4
T−ID2
T−ID1
T−ID2
T−ID6
T−ID3
T−ID3
T−ID5
T−ID1
3
1 7
1 4
2 1
2 6
3 2
3 3
5 1
1 4
2 6
1 7
3
2 1
5 1
3 2
3 3
Abbildung 2.8: Verbundindex als Tabelle und als B*-Bäume, jeweils nach den Tupel-IDs
sortiert
Im Falle eines kompletten Verbundes kann der B*-Baum sequentiell traversiert werden.
Kommen Selektionen hinzu, ergibt sich bei der vorherigen Selektion eine Liste der auszuwählenden Tupel-IDs. Diese wird sortiert, um aus dem entsprechend sortierten B*-Baum
die entsprechenden Verbundpaare in einem Durchlauf auszuwählen. Die referenzierten
Datensätze werden dann vom Externspeicher geholt und unter Beachtung möglicher Projektionsklauseln ausgegeben.
Eine andere Form von Verbundindex lässt sich mit Bitmap-Listen erstellen. Statt
Datensätze oder Speicherseiten der eigenen Relation repräsentieren die einzelnen Stellen
eines Bit-Strings dabei Primärschlüssel oder Listen davon (Tupel-IDs/RowIDs), einer
anderen Tabelle. Werden die Bit-Strings komprimiert, so ergibt sich ein Verbund, der
im Vergleich zu einer materialisierten Sicht eines Verbundes speichereffizienter ist, denn
bei einer materialisierten Sicht werden die RowIDs in der Regel nicht komprimiert (siehe
auch [O9i-DWG] und [O9i-DPTG]).
Änderungsoperationen auf den beteiligten Relationen können sehr umfangreiche Aktualisierungen des Verbundindexes nach sich ziehen. Möglicherweise ist es bei größeren
Änderungen der Relationen günstiger, den Verbundindex komplett neu aufzubauen, statt
viele Änderungen einzelner Zeilen nachzuvollziehen. Daher empfiehlt sich der Einsatz
eines Verbund-Indexes besonders für Anwendungen, die viele Verbund-Abfragen, aber
wenige Datenänderungen nach sich ziehen, wie dies bei Data-Warehouse Anwendungen
oft der Fall ist.
Die Idee einen vorberechneten Verbund zu speichern, lässt sich auf einfache Art und
Weise von einem Zwei-Wege-Verbund auf einen n-Wege-Verbund verallgemeinern. Statt
mehrere zweistellige Verbunde bei mehrstelligen Verbunden zu verknüpfen, kann auch
ein mehrstelliger Verbund vorab berechnet werden. Dazu werden für weitere Attribute
und damit verbundene Verknüpfungen weitere Spalten in der Verknüpfungstabelle be-
KAPITEL 2. VERBUNDE IN DATENBANKEN
19
reitgestellt, was wiederum mehrere B*-Bäume für die entsprechenden Sortierungen nach
sich ziehen kann. Dabei sollte man beachten: Je mehr Verbundoperationen in einem gemeinsamen Index vorberechnet sind, desto spezieller ist sein Einsatzbereich und damit
umso geringer der praktische Nutzen für beliebige Verknüpfungen. Zudem wird der Index
zunehmend wartungsaufwendiger bei Aktualisierungsoperationen.
2.3.2
Verbunde in objektrelationalen Datenbanken
In objektrelationalen Datenbanken gibt es für den Benutzer die Möglichkeit eigene Datentypen (und dazugehörende Methoden) aus den bestehenden Datentypen zu konstruieren.
Diese Flexibilität bringt allerdings mit sich, dass die auf Standarddatentypen basierenden
Indexierungsalgorithmen nicht oder zumindest nicht ohne weiteres, auf die neuen Objekte
angewand werden können.
Die Indexierung zusammengesetzter (oder mehrdimensionaler) Datentypen kann erreicht werden, indem die einzelnen Komponenten dieses Datentyps jeweils einzeln indexiert werden. Bei einer Suche werden dann die Ergebnisse der einzelnen Indexabfragen über mengentheoretische Operationen miteinander verbunden. Dieses Verfahren kann
aber nicht alle Anwendungen abdecken, so ist eine Indexunterstützung für nearest neighbour -Abfragen bei räumlichen Daten nicht ohne weiteres zu bewerkstelligen. Auch ist es
meist nicht sehr effektiv, denn die Eigenschaften der Objekte werden dabei nicht weiter ausgenutzt. Die Methode einzelne Suchschlüsselkomponenten zu einem gemeinsamen
Suchschlüssel zu konkatenieren, verspricht keine Verbesserung, denn bei Ablage dieses
Schlüssels in einem B*-Baum wird er nur nach der ersten Komponente sortiert gespeichert. Ordnungen auf anderen Teilschlüsseln gehen verloren und können bei einer Suche
nicht mehr ausgenutzt werden.
Kapitel 3
Spatial Join Algorithmen
Eine auf den Datentyp angepasste Indexstruktur kann deren Eigenheiten ausnutzen, um
effektiv zu arbeiten. In diesem Kapitel werden einige indexgestützte Verfahren vorgestellen, die dem Verbund räumlicher Objekten dienen. Dabei sind die verwendeten Verbundalgorithmen auf die jeweiligen Indexstrukturen für räumliche Datensätze zugeschnitten,
die daher ebenfalls in diesem Kapitel skizziert werden.
Der indexgestütze Join-Prozess wird normalerweise in zwei Stufen aufgeteilt: In einer
ersten Filter-Phase werden mit Hilfe des Indexes möglichst viele Verbundpaare aussortiert, die nicht der entsprechenden Verbundoperation entsprechen. Da in den Indexen
nicht die tatsächlichen Objektgeometrien hinterlegt sind, sondern meist leichter zu handhabende Approximationen (beispielsweise ein Minimum Bounding Rectangle MBR) kann
der Index nur zur Berechnung einer Kandidatenliste beitragen. In einer zweiten Filterung werden die tatsächlichen Objekt-Geometrien betrachtet, um aus diesen Paaren die
Ergebnis-Menge zu generieren. Da die zweite Phase bei allen Algorithmen gleich ist, sind
dort keine Laufzeitunterschiede zu erwarten. Daher wird die zweite Filter-Phase bei der
Beschreibung der Algorithmen nicht weiter betrachtet.
Auch sind keine prinzipiellen Unterschiede bei der Verwendung verschiedener Operatoren (disjoint, containment, intersection(=overlap), equality, touching) zu erwarten:
Bei vielen Index-Strukturen kann in weiten Teilen nur auf Überlappung oder Disjunktheit geprüft werden. Bei den vorgestellten Baum-Strukturen ist beispielsweise erst auf
der Blatt-Ebene die Unterscheidung möglich.
3.1
indexed nested loops join
Dies ist einer der einfachsten Join-Algorithmus. Dabei werden alle Elemente der einen
Tabelle nacheinander abgearbeitet. Zu jedem Eintrag oa der äußeren Tabelle (oder des
zugehörigen Indexes) werden mittels des Indexes der zweiten Tabelle alle Objekte ob (der
2. Tabelle) gefunden, die dem Vergleichsoperator Θ entsprechen, also etwa ob sich deren
bounding box mit oa schneiden. Existiert auch für die äußere Tabelle ein Index, so kann
dabei sehr einfach eine zusätzliche Selektion stattfinden.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
21
indexed-join1 (A, B: Index, qa : Query, Θ: Operator);
FOR (oa ∈ IndexScan(A,qa )) DO
construct query qb for Θ and oa
FOR (ob ∈ IndexScan(B,qb )) DO
output(oa , ob )
END
END
END
Diese Strategie hat den Vorteil , dass sie praktisch bei allen Indexstrukturen angewand
werden kann.
3.2
R*-tree join
Dieser Algorithmus ist von Brinkhoff, Kriegel, Seeger in [BKS93] vorgeschlagen und dort
noch bezüglich der CPU- und I/O-Performance optimiert. Er ist deutlich leistungsfähiger als der indexed nested loops join, wenn dieser auch auf einer Baumstruktur basiert.
Denn während beim indexed nested loops join zumindest die oberen Knoten sehr häufig durchlaufen werden müssen, werden sie beim R*-Baum-Verbund nur selten besucht,
denn der Algorithmus arbeitet rekursiv und muss damit nicht jedesmal bei der Wurzel
neu beginnen.
3.2.1
Aufbau eines R-Baumes
Ein R-Baum [Gut84] besitzt eine Datenstruktur, die mit denen von B+ -Bäumen vergleichbar ist, aber mehrdimensionale Rechtecke als Objekte beinhaltet. Bei einem R-Baum
handelt es sich um einen ausgeglichenen Baum, dessen innere Knoten (mbr,child)-Paare
beinhalten, wobei mbr ein Minimum Bounding Rectangle und child einen Zeiger auf einen
Nachfolge-Knoten beinhaltet. Die mbr -Einträge werden nach einer Änderung des Baumes
so aktualisiert, dass sie danach wieder das kleinste (achsenparallele) Rechteck enthalten,
das die Rechtecke aller Nachfolger-Knoten umschließt. Ein Blatt beinhaltet (mrb,obj)Paare, die wiederum ein MBR und einen Verweis auf das entsprechende Objekt in der
Datenbank enthalten.
Im R-Baum werden in den Knoten, die üblicherweise die Größe (oder ein Vielfaches)
einer Datenseite des externen Speichers haben, zwischen m und M solcher Paare gespeichert (2 ≤ m ≤ dM/2e) Die Wurzel besitzt wenigstens 2 Nachfolger oder ist selber
ein Blatt ist, in der dann auch weniger als m Knoten gespeichert sein können. Da kein
prinzipieller Unterschied zwischen einem Zeiger auf einen weiteren Nachfolgeknoten und
einem Zeiger auf ein konkretes Datenobjekt besteht, kann man die Knoteneinträge auch
zu (mbr,ref )-Paaren verallgemeinern.
Wie in [BKSS90] gezeigt wird, ist der R∗ -Baum eine besonders effiziente Spezialisierung der R-Bäume. Er unterscheidet sich nur in den Einsetz- und Teilungsmethoden, aber
nicht im Aufbau der Datenstruktur von den ursprünglichen R-Bäumen.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
a
b
3
1
22
a
b
c
4
2
1
c
5
6
7
2
3
4
5
6
7
zu den Datensätzen der Objekte
Abbildung 3.1: Beispiel eines R-Baumes
Der Algorithmus, der dem Einfügen von Knoten in einen Baum implementiert, betrachtet bei R*-Bäumen nicht nur die Vergrößerung der Fläche bei der Auswahl des
Einfügepfades, sondern minimiert ebenfalls die Überschneidungen (bei den Knoten der
vorletzten Ebene), die durch das Einfügen eines neuen Knotens entstehen. Muss ein Knoten geteilt werden, so werden die Rechtecke zunächst in Bezug auf ihre Lage auf den
Achsen des Raumes sortiert. Diejenige Achse wird ausgewählt, die verspricht, dass der
Rand um die zu bestimmenden zwei Gruppen am kleinsten wird. Dann wird eine Verteilung der Einträge in zwei Gruppen entsprechend der gewählten Achse ausgewählt, welche
die Überschneidungen zwischen den beiden Gruppen minimiert.
3.2.2
Spatial Join
Der Basis-Algorithmus für einen räumlichen Verbund mit zwei R-Bäumen mit Wurzeln
A und B funktioniert folgendermaßen:
rtree-join1 (A, B: R-Node);
FOR (EA ∈ A) DO
FOR (EB ∈ B with EB .mbr ∩ EA .mbr 6= ∅) DO
IF ((A is a leaf page) OR (B is a leaf page)) THEN
output(EA , EB )
ELSE
ReadPage(EA .ref); ReadPage(EB .ref);
rtree-join1(EA .ref, EB .ref)
END
END
END
END
Der rekursiv arbeitende Algorithmus wird zunächst mit den Wurzeln der zu verbindenden Bäume aufgerufen. Es folgt ein Tiefendurchlauf durch die beiden Bäume, wobei
diese parallel durchsucht werden.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
23
Zu jedem Eintrag EA des Knotens A wird geprüft, ob die Elemente EB aus B eine
nichtleere Schnittmenge mit EA besitzten. Man beachte hierbei, dass A und B jeweils
auf der gleichen Stufe der entsprechenden Bäume stehen (daher: paralleler Durchlauf).
Werden sich schneidende Einträge gefunden, so wird geprüft, ob es sich dabei bereits um
Blätter einer der Bäume handelt. Dann ist keine weitere Rekursionsstufe mehr nötig und
möglich, denn in wenigstens einem Baum beinhaltet das Objekt bereits den Verweis auf
die Datenbank. Die Funktion output verfolgt denjenigen Baum bis zu den Blättern, der
noch nicht die Blattebene erreicht hat , wobei die MBR des Datenobjektes des Baumes auf
Blattebene berücksichtigt werden sollte. Alle Paare (EAi , EBj ), die sich am Ende dieses
Baumabstieges ergeben, werden als Ergebnis der ersten Filterstufe ausgegeben. Handelt
es sich bei den Knoten beider Bäume bereits um Blätter, so ist das Ergebnis das Paar
(EA , EB ).
Sollte es sich weder bei A noch bei B um ein Blatt handeln, so wird der Algorithmus mit den sich schneidenden Knoten rekursiv aufgerufen, nachdem die entsprechenden
Seiten in den Speicher geladen wurden (falls sie sich noch nicht dort befinden).
Der Algorithmus überprüft alle Elemente in EA .ref und EB .ref. Da die Schnittmenge
der MBRs aber im Allgemeinen kleiner als die einzelnen MBR sind, uns aber nur Elemente aus diesem Schnitt interessieren, ergibt sich eine erste Optimierung, indem man
als weiteren Parameter ein Rechteck angibt, in dem gesucht werden soll.
Vor jeder Rekursion werden die Seiten der referenzierten Knoten in den Speicher geladen. Um die I/O-Zugriffe zu senken, werden üblicherweise Puffer (im Programm oder
vom Betriebssystem/DBMS) verwendet, die den Zugriff auf externen Speicher minimieren
sollen. Ein bereits im Speicher/Puffer befindlicher Knoten soll möglichst zuerst verwendet werden, statt ihn später wieder neu laden zu müssen. Mittels eines Plane-SweepAlgorithmus können die Rechtecke eines Knotens in gewissen Maßen geordnet werden.
Dadurch lassen sich die Vergleiche koordinieren, so dass es (in gewissen Grenzen) möglich ist, sie zu optimieren. Dabei findet dieser Sortiervorgang beim Laden der Seiten in
den Speicher statt, denn die Struktur des R-Baumes soll nicht verändert werden. Das
Sortierung im Speicher beschränkt die Auswahl der anzuwendenden Sortieralgorithmen
auf einfache Typen, da sonst der Performance-Vorteil zunichte gemacht wird, wenn eine
Seite dennoch öfter geladen werden muss.
Eine etwas anderen Weg zur Optimierung dieses Algorithmus wird in [HLR97] vorgeschlagen: Dabei werden die beiden Bäume jeweils ebenenweise betrachtet. Statt aber in
einer Rekursion und damit einer Tiefensuche mögliche Verbundpartner zu suchen, werden
erst alle möglichen Paare auf einer Baumebene bestimmt.
Die Zwischenergebnisse sind dabei nötigenfalls auf externem Speicher zwischenzuspeichern, wenn sie nicht mehr im Hauptspeicher verwaltet werden können. Die Verbundpaare
eines Zwischenergebnisses werden dann geordnet, um untergeordnete Knoten möglichst
selten lesen zu müssen.
Ist dies geschehen, so wird der Verbund für die nächste Ebene berechnet, wobei die
Knoten in der berechneten Reihenfolge untersucht werden.
Statt die Prozedur des normalen R-Baum Verbundes rekursiv zu gestalten, ist es
natürlich auch möglich, die zu untersuchenden Knoten auf einen Stack abzulegen. Beim
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
24
Eintritt in die Prozedur werden jeweils die beiden Elemente entfernt, die beim rekursiven
Aufruf die Wurzeln darstellen. Statt einer neuen Rekursion mit EA .ref und EB .ref werden
diese beiden Elemente auf den Stack abgelegt. Die Prozedur wird in einer Schleife dann
so oft aufgerufen, bis alle Elemente des Stacks entfernt sind.
3.3
Seeded Trees
Ming-Ling Lo und Chinya V. Ravishankar schlagen in [LR94] eine Methode vor, die die
Anzahl der Vergleiche bei den R-Baum-indexgestützten Joins reduzieren soll. Des weiteren bietet sie sich an, wenn nur für einen der beteiligten Datensätze ein Index existiert.
Als Beispiel betrachte man Abbildung 3.2. Dort sind die Bounding-Boxen der Knoten der
Ausgangssituation
Gruppierung bei R−Baum−Erzeugung
für den 2. Datensatz
Datenobjekt im 2. Datensatz
Bounding Box von Baum 1
Günstigere Gruppierung
Bounding Box von Baum 2
Abbildung 3.2: Ungünstige und günstige bounding box -Verteilung in einem Seeded Tree
obersten Ebene eines bereits bestehenden Indexes zu sehen und einzelne Datenobjekte
eines 2. Datensatzes, auf denen ebenfalls ein Index erstellt werden soll. Der übliche Algorithmus würde, wie im mittleren Teil der Abbildung zu sehen ist, möglicherweise kleinere
MBRs erzeugt, die aber jeweils mehrere bounding boxes des 1. Datensatzes schneiden.
Dies würde jeweils mehrere Vergleiche hervorrufen. Ein günstigeren Verteilung ergibt
sich, wenn die Objekte wie im rechten Teil der Abbildung zu sehen gruppiert werden,
denn dadurch reduziert sich die Anzahl der Vergleiche der Knoten des 1. Datensatzes mit
den Knoten des 2. Datensatzes auf der obersten Ebene auf jeweils 1 Paar.
Die Idee von Seeded Trees besteht also darin, eine gewisse Anzahl von Ebenen eines
existierenden R-Baumes für die Konstruktion eines Baumes für den zweiten Datensatz zu
übernehmen. Dadurch kann man die spätere Form des Seeded Trees so beeinflussen, dass
ein Verbund der beiden Datenstrukturen weniger Knoten-Vergleiche und damit weniger
zu lesende Knoten, also Seiten vom externen Speicher benötigt. Die Join-Phase ist mit
der des R-Baumes identisch, denn der Seeded Tree hat eine sehr ähnliche Struktur.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
3.3.1
25
Seeded Tree Konstruktion
Um einen Seeded Tree aufzubauen, wird in der seeding phase eine gewisse Anzahl an
Ebenen eines existierenden R-Baumes herangezogen, um das Aussehen des Trees zu beeinflussen. Dabei können sowohl die bounding boxes als auch die Mittelpunkte der MBRs
des R-Baumes kopiert werden. Lo und Ravishankar ermittelten einen Vorteil, wenn nur
die Mittelpunkte der MBRs kopiert werden (zumindest auf der untersten Ebene, darüber
liegen dann entweder auch die Mittelpunkte der MBRs des kopierten Baumes oder die
MBRs werden wie im R-Baum aus den Nachfolge-Knoten errechnet).
Die kopierten Ebenen nennt man seed levels, die Ebenen darunter grown levels, wobei
die unterste Ebene der seed levels, also die Vorgänger der grown levels, slot-level genannt
werden. Die ref-Komponente der (mbr, ref )-Paare dieser Ebene werden auch slot-pointer
genannt. Dort werden im Laufe der Baumerstellung Unterbäume wachsen, bei denen es
sich um normale R-Bäume handelt.
Initial ist nur die mbr-Komponente auf der slot-level-Ebene besetzt, um zu bestimmen,
in welchen Unterbaum ein neuer Eintrag einzufügen ist. Die ref-Komponente verweist
anfangs auf einen reservierten Wert, z.B. NULL. In der ersten Ebene der grown levels
liegen also Wurzeln von R-Bäumen, oder die slot pointer verweisen auf den initialen
Wert, NULL-Zeiger.
a
d
k
l
e
m
f
n
o
p
q
b
c
g h
i
r s
t
u
v
j
w
x
y
kopieren
der
oberen
Ebenen
zu den Datensätzen in der Datenbank
grown
levels
seed levels
a
d
e
f
b
c
g h
i
j
slot level
slot pointer (initial: NULL)
Abbildung 3.3: Seeded Tree Konstruktion
Während der growing phase werden die Daten-Objekte in den Baum eingefügt. Dazu
wird der Baum von der Wurzel zu den slot-Ebenen durchlaufen, wobei in jeder Ebene
eine passende Richtung gewählt wird. Handelt es sich um das erste Objekt für einen slot
während der Wachstumsphase, so wird ein neuer Knoten alloziiert, das Daten-Objekt in
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
26
diesen Knoten eingefügt, und der slot pointer auf diesen Knoten gesetzt. Ansonsten zeigt
der slot pointer bereits auf die Wurzel eines R-Baumes, in den das Objekt ganz normal
eingefügt wird. Ein Aufsplitten der Wurzel des Teilbaumes wird allerdings nicht weiter in
die seed level weitergeleitet, sondern führt zu einer Aktualisierung des slot pointers auf
die nunmehr neue Wurzel.
Während die MBRs in den Unterbäumen in der Wachstumsphase ständig aktualisiert
werden, muss man dies in den seed levels nicht unbedingt tun, denn sonst riskiert man,
dass sie sich zu sehr von der gewünschten (nämlich der vorgegebenen) Form entfernen.
Man kann sich verschiedene Varianten vorstellen, die MBRs nach einer Einfüge-Operation
z.B. nur bis zu der slot-Ebene zu aktualisieren oder nur die eingefügten Daten, nicht aber
die initialen MBRs auf bestimmten Ebenen zu aktualisieren.
Da zur Konstruktion des Seeded Trees in der Regel nur eine bestimmte Anzahl an
Speicherplätzen für die Knoten im Hauptspeicher zur Verfügung steht, der üblicherweise
von den Knoten benötigte Platz aber weit größer ist, schlagen Lo und Ravishankar vor,
nicht sofort mit der Konstruktion der R-Bäume zu beginnen, sondern die Daten-Objekte
erst in verketteten Listen zu speichern, wobei jedem slot pointer eine Liste zugeordnet
wird. Sollte der Pufferspeicher nicht mehr ausreichen, so werden in einem batch alle Listen,
die einen bestimmten Füllungsgrad überschreiten, auf den externen Speicher geschrieben
(gibt es nicht genug Listen, die den Füllungsgrad überschreiten, so wird der Füllungsgrad
so lange erniedrigt, bis ausreichend viele Listen und damit Daten ausgelagert sind). Dieser
lineare I/O-Zugriff geht viel schneller, als ein zufälliger Zugriff, der beim simultanen Erzeugen der R-Bäume entstehen würde. Sind alle Daten-Objekte den Listen zugeordnet, so
werden aus den einzelnen Listen die R-Bäume generiert. Aufgrund der vielen slots sollten
die einzelnen Teilbäume klein genug sein, um einzeln komplett im Pufferspeicher Platz
zu finden, bevor sie wiederum in einem Rutsch auf den externen Speicher geschrieben
werden können.
Sind alle R-Bäume erzeugt, so werden in der clean-up phase die MBRs auch auf den
seeded levels an die tatsächlichen Gegebenheiten angepasst, d.h. die MBRs werden aus den
jeweiligen Einträgen der untergeordneten Knoten berechnet. Es werden nicht benötigte
slots entfernt und die Datenstruktur konsistent gemacht. (NULL-Zeiger, Unterteilung nach
grown- und seed-Level entfernen, etc.)
Man beachte, dass die gewachsenen Bäume alle unterschiedliche Höhen haben können,
dies aber vom Join-Algorithmus bereits berücksichtigt wird, wenn unterschiedlich hohe
R-Bäume miteinander verbunden werden sollen.
In [LR98] geben Lo und Ravishankar gute“ Grenzen für die Anzahl der slots und
”
die Knoten in der slot-Ebene an, da eine zu große Anzahl davon schnell zu einem großen
Speicherplatz-Verbrauch bei den zur Verfügung stehenden Puffern führt und eine zu geringe Zahl den Join-Algorithmus negativ beeinflusst. Man sollte dabei aber beachten, dass
nur die Effizienz, aber nicht die Funktionsfähigkeit beeinflusst wird. In [LR98] wird ebenfalls vorgeschlagen, die Wurzeln der gewachsenen Teilbäume zusammen in gemeinsamen
Knoten zu lagern (durch geeignete reservierte Einträge getrennt). Bei vielen Teilbäumen
kann es sein, dass die Wurzeln nicht ganz gefüllt sind (und auch nicht mit mindestens m
Einträgen, wie dies bei einem R-Baum für den kompletten Datensatz auf dieser Ebene
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
27
der Fall wäre). Das Zusammenlegen führt zu einer gewissen Speicherplatzersparnis, aber
vor allem zu einem geringeren Puffer-Bedarf während der Join-Phase.
3.4
Spatial Hash-Join
In [LR96] beschreiben Lo und Ravishankar einen Join-Algorithmus, der nicht auf einer
Baum-Struktur beruht, sondern ad hoc eine Datenstruktur für den Join-Prozess aufbaut.
Er soll dennoch mit den Baum-basierten Algorithmen konkurrieren können, auch wenn
diese auf einen bereits vorhandenen R-Baum Index zurückgreifen.
3.4.1
Funktionsweise des Hash-Joins
Hash-Algorithmen benutzen eine Hash-Funktion, die die Tupelmenge in eine gewisse Anzahl von Equivalenzklassen unterteilt. Die Tupel in derselben Klasse werden dann demselben Container (bucket) zugeordnet (partition phase). Sucht man also z.B. in zwei Tabellen
diejenigen Einträge mit der gleichen Produktnummer, so könnten beim Hash-Join die Tupel mit den gleichen Endziffern (bei der Produktnummer) in einem Container landen. Da
die Hash-Funktion für beide Tabellen gleich gewählt wird, braucht man für den eigentlichen Vergleich nur noch die Tupel in den entsprechenden Containern heranzuziehen,
wenn die Join-Attribute verglichen werden (join phase).
Bei geographischen Daten ist diese Strategie allerdings nicht ausreichend. Dazu betrachte man in einem Datensatz die Objekte A und B, in einem anderen Y und Z, wobei
Y sowohl A als auch B überschneidet. (Siehe Abbildung 3.4) Ordnet man nun A und
Y einem Container zu, da sich deren Mittelpunkt auf der linken Halbebene befindet, B
und Z dem Container für die rechte Halbebene, so findet man zwar Überschneidungen
zwischen A und Y, sowie B und Z, aber keine zwischen B +Y.
Y
Container−Grenzen
B
Objekt des 1. Datensatzes
Z
A
Objekt des 2. Datensatzes
Abbildung 3.4: Einfache Container-Zuodnung für Spatial Join
Die einzige Möglichkeit sicherzustellen, dass alle Vergleichspartner in einem Container
landen, besteht in der Regel darin, nur einen einzigen Bucket zu verwenden. Dann entspricht die Performance aber auch nur der des nested loops join. Der Ausweg aus diesem
Dilemma besteht darin, auch verschiedene“ Buckets miteinander zu vergleichen (multiple
”
matching), was aber beim Konzept des relationalen Hash-Joins gerade vermieden werden
soll, oder man teilt einem Objekt mehrere Container zu (multiple assignment), muss also
redundante Daten und eine höhere I/O-Last erzeugen.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
28
Beim spatial Hash-Join bestehen die Partitions-Funktionen aus zwei Komponenten:
Eine Zuweisungsfunktion (assignment function) und einer Menge von Container-Ausdehnungen (bucket extents), jeweils ein bucket extent pro bucket. Eine bucket extent korrespondiert mit einer Region im Gebiet, in dem der Spatial Join berechnet werden soll,
muss aber nicht zwangsläufig zusammenhängend sein. Er wird von der Zuweisungsfunktion benutzt, um einem Datenobjekt ein Bucket zuzuordnen, in der Join Phase dient
er der Identifizierung der Container, die miteinander verglichen werden müssen. Die Zuweisungsfunktion weist die Datenobjekte den Containern zu, je nachdem, wie sie zu den
Container-Ausdehnungen in Beziehung stehen. Je nach Design kommen dafür zum Beispiel die Container in Frage, deren Ausdehnung ein Objekt am meisten überlappt, oder
alle Container, deren Ausdehnung das Objekt schneiden.
In der Join Phase müssen die Container des 1. Datensatzes (innen) mit allen Containern des 2. Datensatzes (außen) verglichen werden, in denen sich überlappende Objekte
befinden können.
Der Hash-Join Algorithmus kann von existierenden Indexen profitieren, da er in der
untersten Ebene des R-Baumes die MBRs der Daten-Objekte findet, und diese somit
nicht selbs berechnen muss.
3.4.2
Beispiele für Zuweisungs- und Ausdehnungsfunktionen
Beispiel 1
Bucket extents
Zuweisungsfunktion
Join-Bucket Paare
multiple assignment
Aufteilung der Kartenfläche in gleich große, nicht überlappende Regionen, z.B. einem regelmäßigem Gitter mit
n × n Zellen. Der innere und äußere Datensatz besitzen
die gleichen Container-Ausdehnungen, die sich während
der Zuweisungsphase nicht ändern.
Ein Datenobjekt wird jedem Container zugewiesen, dessen Ausdehnung das Objekt überlappt. Ein Objekt kann
also in mehreren Buckets vertreten sein.
Vergleiche jeden inneren mit dem entsprechenden äußerem Container, der also die gleiche Ausdehnung besitzt.
Dabei werden Objektpaare, die sich in mehreren Containern überschneiden mehrfach gefunden: Duplikate sollten am Ende entfernt werden.
Nachteilig bei dieser Methode ist, dass die Containergrößen nicht auf die Verteilung
der Objekte eingehen. Einige Buckets können sehr viele Objekte enthalten, während andere nahezu leer sind. Auf Grenzen endende Objekte sollten in beiden Containern abgelegt
werden, dadurch wird die Datenmenge weiter vergrößert. Am Ende der Join Phase ist
noch zusätzlicher Aufwand nötig, um doppelt gefundene Objektpaare zu eleminieren.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
Beispiel 2
Bucket extents
Zuweisungsfunktion
Join-Bucket Paare
29
multiple matching
Begonnen wird wird wiederum mit n × n Zellen, die
nicht überlappend die gesamte Karte bedecken. Innerer und äußerer Datensatz beginnen mit den gleichen
initialen bucket extents, doch werden diese beim Zuweisen der Objekte vergrößert, so dass sie das ganze
Objekt umschließen. Daher werden sich die ContainerAusdehnungen am Ende der Zuweisungsphase in der Regel unterscheiden.
Jedes Objekt wird dem Container zugewiesen, dessen
Fläche am wenigsten vergrößert wird. Bei mehreren
Kandidaten kommt das Objekt in den Bucket mit dem
nächsten Schwerpunkt.
Jeder innere Container wird mit jedem äußeren Container verglichen, dessen Ausdehnung sich überschneidet.
In der Join-Phase muss bei dieser Methode die Reihenfolge der Container sorgfältig
ausgewählt werden, wenn man einen Puffer ausnutzen möchte und es vermeiden will, die
Buckets mehrfach zu laden.
Beispiel 3
Bucket extents
Zuweisungsfunktion
Join-Bucket Paare
Lo und Ravishankars Vorschlag - multiple assignment
Die inneren Bucket Extents werden mittels eines Bootstrap-Verfahrens (beschieben in [LR95]) mit eine Anzahl Punkte initialisiert. Während der Zuweisung wachsen die Bucket Extents, um die Objekte zu umgeben.
Die äußeren Buckets werden mit den Ausdehnungen der
inneren initialisiert und verändern sich nicht weiter.
Beim inneren Datensatz werden die Objekte den Bucket
Extents so zugewiesen, wie dies auch bei den R-Bäumen
(und Seeded Trees) geschieht. Die MBRs werden nur
minimal vergrößert und Überlappungen möglichst vermieden. Im äußeren Datensatz muss jedes Objekt allen Containern zugewiesen werden, deren Ausdehnung
überlappt wird. Ist dies nicht der Fall, wird kein Eintrag
benötigt, da das Objekt dann für den Join irrelevant ist.
Da die Ausdehnungen der Container gleich sind, wird für
jeden inneren nur ein äußerer Container herangezogen.
Andere Überschneidungen brauchen nicht berücksichtigt
werden, da die Datenobjekte des äußeren Datensatzes
sonst schon dupliziert worden wären.
Um externe Speicherungen möglichst effizient zu gestalten, kann wie schon bei den
Seeded Trees eine Batch-Write Strategie angewendet werden, wenn die Puffer in der
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
30
Zuweisungs-Phase einen bestimmten Füllungsgrad erreicht haben. Der Vergleich der Objekte in den einzelnen Containern in der Join-Phase kann im einfachsten Fall über einen
nested loops join, oder besser noch ähnlich dem indexed nested loops Join (siehe 3.1)
stattfinden. Dazu baut man zu einem der Datensätze einen kleinen R-Baum, der als
Index genutzt wird, wenn die anderen Objekte der Reihe nach abgearbeitet werden.
3.5
Z-Codes und Standard-Indexe
Eine andere Möglichkeit einen räumlichen Verbund herzustellen, ergibt sich aus einer
anderen Indexierungsmöglichkeit. In [OM84] wird der zu indexierende Raum in gleichmäßige, sich nicht überlappende Regionen aufgeteilt. Im 2-dimensionalen Fall erzeugt man
eine Einteilung in 2d × 2d Kacheln. Wenn man die Aufteilung des Raumes in jede Achse
binär nummeriert, so werden die Kacheln eindeutig über einen Bit-String identifiziert, der
durch Verschachtelung der Bit-Folgen der Achsen entsteht (siehe dazu Abbildung 3.5).
Dies entspricht einer (rekursiven) N-förmigen Nummerierung der Kacheln, genannt ZOrdnung. (Ändert man die Reihenfolge der Verschachtelung so ergeben sich die Z-Form.
Die Idee, den Raum in disjunkte Rechtecke zu unterteilen, die mittels eine space-filling
curve geordnet und nummeriert werden ist schon sehr alt und wurde zuerst 1890 von
Peano veröffentlicht [Pea90].) Mittels dieser Nummerierung werden die Kacheln linear
geordnet, wobei räumliche Nähe in dem Sinne erhalten bleibt, dass die Hamming-Distanz
der Bit-Strings benachbarter Kacheln klein ist.
2.+4. bit
2. bit
01
1
11
11 0101 0111 1101 1111
10 0100 0110 1100 1110
01 0001 0011 1001 1011
0
00
0
10
1
1. bit
00 0000 0010 1000 1010
00
01
10
11
1.+3. bit
Abbildung 3.5: Aufteilung des Raumes: Z-Code
Objekte werden nun indexiert, indem man zunächst feststellt, welche Kacheln von
einem Objekt geschnitten werden. Anschließend bestimmt man eine Menge von Kacheln
(sogenannten Z-Elemente oder Z-Codes), die das Objekt repräsentieren. Der Prozess, die
Z-Element-Menge zu bestimmen, wird Dekomposition genannt. Die Z-Elemente bestehen
aus den Präfixen von Bit-Strings. Schneidet ein Objekt beispielsweise die Kacheln 0010,
0011, 0100 und 0110, so ergibt sich die Z-Element-Menge: {001, 0100, 0110} (man beachte,
dass 0010 und 0011 zu 001 zusammengefasst werden (vergleiche dazu das Polygon in
Abbildung 3.6).
Es gibt einige Alternativen zur Dekomposition eines Objektes. Statt genau die Elemente zu bestimmen, die das Objekt schneidet, kann auch auch ein einziges Z-Element
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
11
11
10
10 0100 0110
01
01
00
00
00
01
10
11
11
31
Polygon:{001,0100,0110}
Kreis:{11}
001
00
01
10
11
Abbildung 3.6: Z-Elemente von Objekten
verwendet werden, welches das ganze Objekt umschließt. Liegt ein Objekt allerdings
ungünstig, so kann dieses Z-Element allerdings sehr groß sein und den Index damit unbrauchbar machen (genau ein Z-Code für B in Abbildung 3.7) Berechnet man zunächst
die bounding box eines Objektes, und daraus die Z-Element-Menge, so ist die Bestimmung der geschnittenen Kacheln wesentlich einfacher. Dies hat allerdings den Nachteil,
unregelmäßig geformte Objekte schlechter zu repräsentieren (3. v.l. in Abbildung 3.7, die
bounding box zu A ist rot dargestellt) als die Z-Elemente, die man erhält, wenn man die
exakte Geometrie eines Objektes verwendet (2. v.l. in Abbildung 3.7).
A
011
01
0100
1
B
exaktes Objekt A
MBR von A
genau ein Z−Code für B
Abbildung 3.7: Verschiedene Dekompositionsmöglichkeiten
Die bei der Dekomposition gefundenen bit-strings lassen sich lexikographisch ordnen,
damit qualifizieren sie sich als Schlüssel in einem B*-Baum, wie ihn die meisten Datenbanken als Index-Struktur unterstützen. Das Polygon aus Abbildung 3.6 würde unter den
Schlüsseln 001, 0100 und 0110 in einem B-Baum indexiert.
Ist ein Element B in einem anderen (A) enthalten, so müssen die z-Elemente von A
jeweils die Präfixe der Elemente von B sein. Schneiden sich zwei Elemente, so besitzen
sie jeweils ein gemeinsames Element bzw. wenigstens ein Z-Element ist das Präfix eines
Elementes des anderen Objektes. Man beachte, dass sich die einzelnen Elemente zweier
Objekte nur entweder enthalten können (das eine ist Präfix eines anderen), bereits gleich,
oder nichtüberschneidend sind. Es gibt keine Überschneidungen in dem Sinne, dass es bei
Elementen A und B eine nichtleere Schnittmenge gibt, die wiederum sowohl von A als
auch B verschieden ist.
Für einen räumlichen Verbund (beschrieben in [OM88]) nutzt man diese Eigenschaft
aus, um Schnitte und Überdeckungen zu finden. Dazu muss auf den zu verbindenden
Tabellen jeweils die gleiche“ Einteilung der Kacheln existieren. Die bit-strings können
”
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
32
theoretisch unterschiedlich lang sein, da bei einer Erhöhung der Auflösung die Präfixe
erhalten bleiben. Es kann dann natürlich vorkommen, dass ein Objekt feiner repräsentiert
wird, also statt einer Zeichenkette 01 die Elemente 0101, 0110 und 0111 erhält (aber
nicht 0100). Daraus resultieren mehr zu speichernde Einträge, es ergeben sich aber keine
Vorteile, falls die andere Tabelle nur mit 2 Bit arbeitet, also ohnehin nur auf das Präfix
01 getestet wird.
Zur Berechnung eines joins müssen alle Objekte der beiden Tabellen indexiert sein.
Dazu werden alle Objekte decomposed, also in Elemente aufgeteilt, die wiederum mit
einer Kennzeichnung auf das zugehörige Objekt in der jeweiligen Indexstruktur (z.B.
B+-Baum) abgespeichert werden. Während des Join-Vorganges werden die B+Bäume in
der lexikographischen Ordnung der gespeicherten bit-strings ausgelesen, d.h. man liest
001 vor 01 vor 010 etc. Man kann sich die Bäume also wie Sequenzen vorstellen, die von
vorne nach hinten gelesen werden.
Man betrachte als Beispiel Abbildung 3.8, mit den folgenden Sequenzen:
obere Tabelle: 001(B), 0011(A), 1001(B)
untere Tabelle: 001(C), 100(D)
: A={0011}
11
11
: B={001,1001}
10
01
00
01
00
10
A
B
00
01
10
11
00
01
11
11
11
10
!
C
10
10
:C={001}
!
!
01
00
00
01
00
10
D
:D={100}
01
11
00
01
10
11
Abbildung 3.8: Verschachtelung von Objekten
Man verwendet für jede Sequenz einen Cursor. Desweiteren benötigt man jeweils einen
Stapelspeicher, auf dem man sich die gerade bearbeiteten Elemente merkt. Problematisch
sind die ineinander verschachtelten Objekte, wo ein z-element von einem größeren zelement eines anderen Objektes überdeckt wird (im Beispiel ist dies bei A und B der
Fall). Folgender Algorithmus findet alle sich überschneidenden Paare:
z-tree-join (L,R: Sequenz);
L-Stack, R-Stack: Stack;
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
33
result: List;
event: Element;
L.start(); R.start();
WHILE ( NOT L.eof() && R.eof() && L-Stack.empty() && R-Stack.empty() ) DO
event=min(lowest(L.current()), lowest(R.current()),
highest(L-Stack.top()), highest (R-Stack.top());
SWITCH (event){
CASE lowest(L.current()):
enter-element(L, L-Stack); BREAK;
CASE lowest(R.current()):
enter-element(R, R-Stack); BREAK;
CASE highest(L-Stack.top()):
exit-element(L-Stack, R-Stack, result); BREAK;
CASE highest(R-Stack.top()):
exit-element(R-Stack, L-Stack, result); BREAK;
}
END;
return result;
END
Dazu kommen die Prozeduren enter-element und exit-element, die die Elemente auf
den Stack schreiben und entfernen, sowie für das Füllen der Ergebnisliste zuständig sind.
Die Funktionen lowest und highest liefern zu einem z-element den Wert der niederwertigsten bzw. höchstwertigsten Kachel des Elementes. Verwendet man vier Bit, so ergibt
dies lowest(10)=1000 und highest(10)=1011. enter-element und exit-element sind
folgendermaßen definiert:
enter-element (A: Sequenz, A-Stack: Stack);
A-Stack.push(A.current);
A.next();
END
exit-element (A-Stack,B-Stack: Stack, result: List);
report-pairs(A-Stack.top(), B-Stack, result);
A-Stack.pop();
END
Dabei sucht report-pairs(A,B-Stack,result) die Elemente des B-Stack nach einem gemeinsamen Präfix mit dem Element A durch und fügt die zugehörigen Objekte in die
Ergebnisliste result ein, falls sie sich dort noch nicht befinden.
Zur Funktionsweise des Algorithmus: Die Haupt-Prozedur läuft durch beide Sequenzen
und schiebt die Elemente im Laufe der Zeit auf die zugehörigen Stapelspeicher. Sind
die Stapel leer und die Sequenzen durchlaufen, so ist man fertig. Dies geschieht in einer
Schleife, an deren Anfang jeweils das weitere Vorgehen entschieden wird. Dazu betrachtet
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
34
man die Kacheln der Elemente, die sich an den aktuellen Positionen von Stapel und
Sequenz befinden. Besitzen die Elemente einer Sequenzen eine Kachel, die numerisch
kleiner als die größte Kachel der oberen Elemente auf einem der Stacks ist, so kann es
eine Überschneidung geben. In enter-element wird die entsprechende Sequenz weiter
ausgelesen und das Element auf den zugehörigen Stack verschoben. Dies kann nur für
Elemente geschehen, die in den Elementen des Stapelspeichers enthalten sind oder das
gleiche Z-Element besitzen, sowie bei leerem Stapel. Größere“ Elemente kommen in der
”
Sequenz zuerst, wurden also schon auf den Stapel befördert, oder das oberste Element
des Stapels hat einen kleineren highest-Wert, dann würde es aber bei exit-element
zuerst aus dem Stapel entfernt. Sind keine Elemente mit kleinerem lowest-Wert mehr
in der Sequenz, so werden die Elemente der Stapelspeicher miteinander verglichen und
entfernt. Dazu wird in exit-element das oberste Element des Stapels mit dem niedrigsten
highest-Wert mit den Elementen des anderen Stapels auf gemeinsame Präfixe verglichen
und die zugehörigen Objekte der Ergebnisliste zugefügt. Als Beispiel zur Entwicklung des
Stapels und dem Auslesen der Sequenzen betrachte man noch Abbildung 3.9.
Die Laufzeit des Verbundes ist in etwa linear zur Anzahl der Elemente in den BBäumen. Die Element-Zahl hängt wiederum mit dem Feinheitsgrad der Kachelung zusammen. Erhöht man den Feinheitsgrad und damit die Anzahl der Elemente je Objekt,
so werden weniger Paare gefunden, die sich tatsächlich nicht überschneiden, sondern nur
aufgrund großer Kacheln eine gemeinsame Kacheln belegten. Dafür erhöht sich die Laufzeit des Verbundes entsprechend. In [OM88] wird statt eines einfachen A.next() eine etwas
aufwendigere Funktion zum Fortschreiten in den Sequenzen verwendet, die offensicht”
lich“ überflüssige Einträge überspringt, so dass sich eine sublineare Laufzeit ergeben kann.
KAPITEL 3. SPATIAL JOIN ALGORITHMEN
Stack:
35
L−Stack:
−
Sequenz:
L: 001(B), 0011(A), 1001(B)
R−Stack:
−
R: 001(C), 100(D)
L−Stack:
001(B)
L: 0011(A), 1001(B)
R−Stack:
−
R: 001(C), 100(D)
L−Stack:
001(B)
L: 0011(A), 1001(B)
R−Stack:
001(C)
R: 100(D)
L−Stack:
001(B) 0011(A)
L: 1001(B)
R−Stack:
001(C)
R: 100(D)
L−Stack:
001(B)
L: 1001(B)
R−Stack:
001(C)
R: 100(D)
L−Stack:
−
L: 1001(B)
R−Stack:
001(C)
R: 100(D)
L−Stack:
−
L: 1001(B)
R−Stack:
−
R: 100(D)
L−Stack:
−
L: 1001(B)
R−Stack:
100(D)
R: −
L−Stack:
1001(B)
L: −
R−Stack:
100(D)
R: −
L−Stack:
−
L: −
R−Stack:
100(D)
R: −
−
R−Stack: −
L−Stack:
L: −
R: −
gefundene Paare:
(A,C)
(A,C), (B,C)
(A,C), (B,C)
(A,C), (B,C)
(A,C), (B,C)
(A,C), (B,C), (B,D)
(A,C), (B,C), (B,D)
Abbildung 3.9: Beipiel zum z-tree-join
Kapitel 4
GiST-Indexe
Um den gesteigerten Anforderungen an die in einer Datenbank zu speichernden Daten
gerecht zu werden (Geographische Daten, CAD-Datensätze, Dokument-Bibliotheken, Fingerabdrücke), wurden im Laufe der Zeit zwei wesentliche Ziele bei der Erforschung von
Suchbaum-Technologien verfolgt:
1. Spezialisierte Suchbäume: Es wurde eine sehr große Anzahl von Suchbäumen für
spezifische Probleme entwickelt. Darunter so bekannte, wie die R-Baum-Varianten
zur Suche in räumlichen Datensätzen. Obwohl diese Suchbäume einen Durchbruch
im jeweiligen Fachgebiet darstellen können, sind sie doch sehr aufwendig in der
Implementierung und Wartung. Neue Anwendungen müssen in der Regel von Grund
auf neu entwickelt werden. Das betrifft selbst grundlegenden Baumoperationen,
wie Suche, Einsetzen, Struktur-Wartung und Synchronisation bei konkurrierendem
Zugriff.
2. Suchbäume für erweiterbare Datentypen: Alternativ zur Entwicklung neuer Strukturen können bestehende Datenstrukturen, wie B*-Bäume und R-Bäume, bezüglich
der Datentypen, die sie unterstützen, erweiterbar gemacht werden. So können B*Bäume zur Indexierung von Daten benutzt werden, auf denen sich eine lineare Ordnung definieren lässt. Die Menge der Datentypen, die damit erfasst werden kann,
ist damit zwar deutlich größer, aber die Anfragen beschränken sich weiterhin auf
die Möglichkeiten des zugrunde liegenden Baumes. Bei B*-Bäumen sind dies also
Anfragen auf Gleichheit oder Wertebereiche, bei R-Bäumen bleibt es bei Gleichheit,
Überlappung und Überdeckung.
Dieser Mangel an Flexibilität bei den Anfragen führt zu Problemen bei der Entwicklung neuer Anwendungen. Es ist eher unwahrscheinlich, dass Anfragen auf lineare
Ordnungen oder räumliche Gegebenheiten auch für neue Datentypen angemessen
sind.
Um die Beschränkungen der beiden Strategien zu überwinden, stellen J.M. Hellerstein,
J.F. Naughton und A. Pfeffer in [HNP95] eine dritte Möglichkeit vor, um SuchbaumTechnologien zu erweitern.
KAPITEL 4. GIST-INDEXE
37
Dort wird eine neue Datenstruktur namens Generalized Search Tree (verallgemeinerter
Suchbaum, kurz: GiST) eingeführt, die sowohl bezüglich der unterstützten Datentypen,
als auch der möglichen Anfragen leicht erweiterbar ist. Die Konfiguration eines GiST zur
Darstellung eines bestimmten Baumtyps geschieht über die Anpassung von lediglich sechs
Methoden, die in der GiST-Basisklasse nur abstrakt deklariert sind.
4.1
Überblick über GiST
Bei einem verallgemeinerten Suchbaum handelt es sich um einen ausgeglichenen Baum
mit variablem Verzweigungsgrad. Die Wurzel besitzt einen Verzweigungsgrad zwischen 2
und M , alle anderen Knoten zwischen kM und M , wobei für den minimalen Füllfaktor
k gilt: M2 ≤ k ≤ 12 .
Die Knoten enthalten Einträge der Form E = (p, ptr), bestehend aus einem Prädikat
p und einem Zeiger ptr, der bei internen Konten auf einen Nachfolgeknoten und bei
Blättern des Baumes auf Tupel (oder Objekte) in einer Datenbank verweist. Die im GiST
zu speichernden Daten werden also nur in den Blättern abgelegt, die alle den gleichen
Abstand zur Wurzel haben. Das Prädikat klassifiziert die über ptr erreichbaren Knoten
oder Datensätze: Sie dürfen der entsprechenden Eigenschaft nicht widersprechen, bzw.
alle darüber erreichbaren Knoten besitzen diese Eigenschaft. Im Gegensatz zu B*-Bäumen
oder R-Bäumen muss es sich bei den Prädikaten nicht zwangsläufig um kontinuierliche
Bereiche handeln, es sind beliebige Sub-Kategorien möglich, wie etwa ist sternförmig“,
”
konvex“ oder ungerade“, aber natürlich gehen auch (mehrdimensionale) Intervalle, in
”
”
denen sich dann die über ptr erreichbaren Daten befinden, je nach Anforderung an die
zu speichernden Daten.
p1 ptr1
p11 ptr11 p12 ptr12
p2 ptr2
p21 ptr21 p22 ptr22 p23 ptr23
Zeiger auf
DB-Tupel oder -Objekte
Abbildung 4.1: Prädikate und Pointer in den GiST-Knoten
Möchte man einen neuen Baumtyp erstellen, erstellt man eine neue Unterklasse der
Basisklasse GiST. Die möglichen Ausprägungen dieses Baumtyps sind dann die Objekte
vom Typ der Unterklasse. Die Spezialisierung geschieht, indem man sechs Methoden neu
definiert, die in der GiST-Klasse nur abstrakt definiert sind. Die Methoden des GiST
rufen dann während der Suche, dem Einsetzen und Löschen im Baum die Methoden der
Unterklasse auf und können somit auf die Bedürftnisse des zu speichernden Datentyps
angepasst werden. Folgende Methoden werden für eine neue Klasse benötigt:
KAPITEL 4. GIST-INDEXE
38
Consistent(E,q): Zu einem Knoten E = (p, ptr) und einem Anfrageprädikat q wird
false zurückgegeben, wenn sicher ist, dass sich die Prädikate widersprechen, ansonsten gibt man true zurück.
Es ist nicht zwingend notwendig, hier akkurat vorzugehen, da der Algorithmus auch
bei fälschlicherweise zurückgegebenem wahr richtig funktioniert. Dann wird aber die
Performance beeinträchtigt, da Teilbäume unnötigerweise untersucht werden.
Union(P ): Zu einer Menge P = {E1 , E2 , . . . , En } von Knoten Ei = (pi , ptri ) gibt die
Funktion ein Prädikat r zurück, welches für alle Tupel gültig ist, die unter ptr1
bis ptrn abgelegt sind. Dazu bestimmt man ein r mit gemeinsamen Eigenschaften
aller pi . Dies kann z.B. ein alle pi umschließendes Intervall (B-Baum) oder Rechteck
(R-Baum) sein.
Compress(E): Zu einem Knoten E = (p, ptr) gibt man einen Knoten (π, ptr) zurück,
wobei π einen komprimierten Repräsentanten von p darstellt. In einem R-Baum
wäre das beispielsweise die bounding box eines Polygons.
Decompress(E): Zu einem komprimierten Knoten E = (π, ptr) wird ein Eintrag (r, ptr)
zurückgegeben, so dass r ein gültiges Prädikat für das p ist, aus dem π bei Compress
hervorgegangen ist. Für einen R-Baum wäre Decompress die Identität: Die bounding
box ist selbst bereits ein Polygon, welches das ursprüngliche Objekt umschließt.
Penalty(E1 ,E2 ): Zu zwei gegebenen Knoten E1 = (p1 , ptr1 ), E2 = (p2 , ptr2 ) wird ein
Strafmaß berechnet, das entsteht, wenn E2 in den Teilbaum, der bei E1 beginnt,
eingefügt wird. Damit soll beim Einsetzen oder Teilen eines Knotens entschieden
werden, wo ein Knoten zu platzieren ist. Typischerweise wird der Größenanstieg des
Prädikates genommen, etwa size(Union({E1 , E2 }))−size(p2 ), mit einer geeigneten
Funktion size, die bei einem R-Baum beispielsweise die Fläche eines Prädikats (also
eines MBRs) berechnet.
PickSplit(P ): Gibt zu einer Menge P mit M + 1 Einträgen eine Partition in zwei
Teilmengen P1 , P2 zurück, die jeweils mindestens kM Einträge besitzen (hier wird
also der minimale Füllfaktor kontrolliert). Hier sollte man versuchen, die Menge
möglichst gut“ zu teilen. Für R-Bäume bedeutet dies zum Beispiel: Geringe Über”
lappung, kleine Flächen und niedrige Umfänge der MBRs um die sich ergebenden
Teilmengen.
Wenn die aufrufende Anwendung die Datensätze - insbesondere die Schlüssel - bereits
in einer für den Baum geeigneten Form bereitstellt, so ist es möglich, für Compress und
Decompress jeweils die Identitätsfunktion zu wählen. Eine interessante Möglichkeit ergibt
sich für Bäume, deren Wertebereich mit einer Ordnung versehen ist. Später wird man
sehen, dass dafür aus Effizienzgründen eine etwas andere Speicherung im GiST gewählt
werden kann. Für den Fall der Speicherung von Intervallen als Prädikat, kann Compress
für den linkesten Eintrag eines internen Knotens ein Prädikat der Größe Null liefern, für
die anderen Einträge im internen Knoten nur die linke Grenze des Intervalles. Decompress
KAPITEL 4. GIST-INDEXE
39
liefert dann wieder ein Intervall zurück, welches aus der vorhandenen linken Grenze und
dem Eintrag des nächsten Knotens generiert wird. Beim linkesten Eintrag verwendet man
−∞ und die linke Grenze des nächsten Eintrages, der sich auch in einem anderen Knoten
befinden kann, oder ∞, falls es keinen größeren“ Eintrag mehr gibt. Daraus ergibt sich
”
eine Speicherung von n − 1 Schlüsseln für n Einträge im Knoten, wie dies auch in B*Bäumen üblich ist.
Hat man diese Methoden für den gewünschten Datentyp implementiert, so können die
vom GiST bereitgestellten Suchbaummethoden, die im Folgenden kurz skizziert werden,
diese nach Bedarf aufrufen. Die Methoden Compress und Decompress werden jeweils
aufgerufen, wenn ein neuer Schlüssel in einen Knoten eingefügt bzw. ausgelesen wird.
Dies geschieht implizit und wird im Folgenden nicht weiter beschrieben.
Suche: Zu einem Prädikat q wird ausgehend von der Wurzel R eines GiST eine Tiefensuche durchgeführt. Dazu wird zu jedem Eintrag E des Knotens mittels der Methode
Consistent(E, q) herausgefunden, ob der Teilbaum oder Datensatz als Ergebnis in
Frage kommen kann. Bei internen Knoten wird die Suche mit dem entsprechenden
Teilbaum rekursiv weitergeführt, Blätter können anhand der tatsächlichen Datenbankeinträge genauer überprüft werden (oder man überlässt dies der aufrufenden
Anwendung, indem das Tupel einfach der Ergebnismenge zugefügt wird).
Suche in linearen Ordnungen: Ist der zu indexierende Wertebereich mit einer linearen Ordnung versehen, und bestehen die zu unterstützenden Anfragen aus Gleichheit und Wertebereichen, so kann die Suche noch effektiver gemacht werden, indem
man bei der Anlage der Spezialisierung eine zusätzliche Methode Compare(E1 , E2 )
implementiert, und ein Flag isOrdered setzt. Compare liefert zurück, welches der
zu den Knoten gehörenden Prädikate bezüglich der Ordnung kleiner“ ist. Die Ein”
träge werden in den Knoten geordnet abgelegt. Bei der Suche kann dann erst der
kleinste das Suchprädikat erfüllende Eintrag, und dann alle weiteren berücksichtigt werden, bis das Prädikat nicht mehr erfüllt ist. Die restlichen Einträge dieses
Knotens brauchen nicht weiter untersucht werden. Die Methoden eines geordneten
Baumes müssen sicherstellen, dass sich zwei verschiedene Einträge eines Knotens
nicht überlappen. Consistent(E1 , E2 ) muss dazu für jedes Paar von Einträgen E1 , E2
eines Knotens false liefern.
Einsetzen: Anhand des Prädikats des einzusetzenden Eintrags E wird der Knoten im
GiST gesucht, wo der neue Eintrag eingefügt werden soll. Dazu wird, beginnend bei
der Wurzel, jeweils Penalty(F ,E) für alle Einträge F eines Knotens aufgerufen, und
zu dem Eintrag mit der geringsten Strafe der zugehörige ptr verfolgt, bis man einen
Knoten einer vorher anzugebenden Stufe erreicht hat. Für das Einsetzen neuer Knoten in den GiST ist dies die Blattebene. Ist dort noch ausreichend Platz, so wird
der Eintrag in den Knoten eingefügt. Handelt es sich um einen geordneteten Baum,
so verwendet man Compare, um die richtige Position zum Einfügen im Knoten zu
finden. Sollte nicht mehr ausreichend Platz vorhanden sein, so muss der Knoten
geteilt werden. Dazu wird mittels PickSplit die beste Partition der Einträge des
KAPITEL 4. GIST-INDEXE
40
Knotens (und des neuen Eintrages) in zwei Teile gesucht. In geordneten Bäumen
muss PickSplit die Ordnung erhalten, also alle Einträge im linken Teil der Partition
müssen bezüglich der durch Compare festgelegten Ordnung kleiner sein als im rechten Teil. Steht die Partition fest, so verbleibt der eine Teil im aktuellen Knoten, der
andere wird in einem neuen Knoten gespeichert. Dieser neue Knoten wird in den
Vorgänger des ursprünglichen Knotens eingefügt, wobei sich bei Platzproblemen im
Vorgänger diese Methode des Aufteilens und Einsetzens bis zur Wurzel fortsetzen
kann. Ist in der Wurzel nicht ausreichend Platz, so wird sie ebenfalls aufgeteilt und
eine neue Wurzel des Baumes installiert, welche die beiden aus der alten Wurzel
entstandenen Knoten aufnimmt.
Die Prädikate der Knoten, die von Änderungen betroffen sind, müssen angepasst
werden. Dazu wird, beginnend auf der Ebene, die auf die Blattebene zeigt, für einen
Eintrag E = (p, ptr), dessen Teilbaum unter ptr geändert wurde, Union mit den
Einträgen des Teilbaumes aufgerufen, und p entsprechend korrigiert. Dies setzt sich
gegebenenfalls bis zu den Einträgen der Wurzel fort.
Löschen: Um einen Eintrag E = (p, ptr) aus einem GiST zu löschen, sucht man zuerst
mittels der Such-Methode über das Prädikat p das Blatt, in dem sich E befindet.
E wird aus dem Blatt entfernt. Hierbei kann es passieren, dass nun weniger als
kM Einträge im Knoten verbleiben. Je nachdem, ob man sich in einem geordneten
Baum befindet, oder isOrdered nicht gesetzt ist, kann jetzt unterschiedlich verfahren
werden.
In geordneten Bäumen wird die von B*-Bäumen bekannte borrow or coalesce- (borgen oder verschmelzen-) Technik verwendet: Sind in einem (gemäß der Ordnung)
Nachbarknoten mehr als 2kM Einträge, so werden diese gleichmäßig auf den aktuellen und den Nachbarknoten aufgeteilt. Ansonsten wandern alle Einträge des
zu kleinen Knoten in den Nachbarknoten. Der leere Knoten, sowie der Eintrag im
Vorgängerknoten auf diesen Knoten, werden entfernt. Sollten dadurch wiederum zu
wenige Einträge im Vorgängerknoten entstehen, setzt sich der borrow or coalesceProzess nötigenfalls bis zur Wurzel fort. (Siehe dazu auch [Com79].)
Ist der Baum nicht geordnet, so wird eine Technik, die auch bei R-Bäumen verwendet wird, herangezogen (vgl. [Gut84]). Sind in einem Knoten zu wenige Einträge,
so merkt man sich die Einträge und deren Stufe im Baum in einer Menge Q. Der
Eintrag im Vorgängerknoten auf den leeren“ Knoten wird entfernt (und sollte sich
”
dadurch wieder ein unterfüllter Knoten ergeben, so setzt sich das Merken der Einträge in Q und Entfernen aus dem Vorgängerknoten notfalls bis zur Wurzel fort).
Anschließend werden die Elemente in Q einzeln wieder in den Baum eingesetzt,
wobei die Stufe, die man sich gemerkt hat, beim Einsetzen berücksichtigt wird.
Bei beiden Vorgehensweisen werden die Prädikate für die Teilbäume jeweils an die
aktuelle Situation angepasst, um sie so spezifisch wie möglich zu halten. Hat die
Wurzel nur noch einen Unterknoten, so wird dieser zur neuen Wurzel des GiST,
und die alte Wurzel gelöscht.
KAPITEL 4. GIST-INDEXE
41
In manchen Anwendungen, in denen nach einem Löschvorgang ein baldiges Einsetzen von neuen Knoten erwartet wird, kann es nützlich sein, dass unterfüllte Knoten
nicht sofort entfernt werden (siehe dazu [JS93]). Dann reicht es aus, die Prädikate
der Knoten anzupassen. Die unterfüllten (oder leeren) Knoten verbleiben im Baum.
Derzeit sind drei GiST-Implementierungen im Internet zu finden:
• Die Universität Berkeley entwickelte eine in C++ verfasste Implementierung libgist,
die im April 2000 in der (bisher abschließenden) Version 2.0 freigegeben wurde.
• An der Universität Kapstadt entwickelte man 1997 aus einer frühen Version (0.9)
der libgist eine Portierung nach JAVA.
• Desweiteren existiert eine Implementierung, die in die Datenbank PostgreSQL eingebunden ist und dort derzeit (Juni 2003) auch verwendet und weiter gepflegt wird
([GiST-PSQL]). Insbesondere verwendet sie ein Paket namens PostGIS, welches
von Refractions Research Inc. unter der GPL ([GPL]) veröffentlicht wurde. PostGIS ([GiST-PGIS]) soll in der Version 1 (derzeit ist 0.7.5 aktuell) PostgreSQL zu
einer OpenGIS konformen räumlichen Datenbank erweitern (bezüglich der Simple
Features Specification for SQL).
Da diese Arbeit eine bereits bestehende Anbindung der libgist an eine Oracle-Datenbank
um räumliche Verbunde erweitern soll, ist hier insbesondere die Implementierung aus Berkeley interessant:
4.2
libgist der University of California at Berkeley
An der Universität Berkeley wurde von 1997 bis 2000 eine GiST-Implementierung namens
libgist in C++ erstellt. Diese wird im Folgenden kurz vorstellen möchte, da sie im Rahmen
dieser Diplomarbeit verwendet wird.
4.2.1
GiST-Erweiterungen
Die libgist enthält einige Erweiterungen des GiST-Konzeptes, die in [Aok98] vorgeschlagen
werden. Dies sind u.a.: Eine Cursorerweiterung, um statt einer Tiefensuche mittels eines
Stacks auch andere Reihenfolgen zu ermöglichen, in denen die Knoten bei der Suche durchlaufen werden. Außerdem kann ein Status zum aktuellen Suchlauf gespeichert werden. So
kann in R-Bäumen mit einer Prioritätswarteschlange auch eine nearest-neighbour-Suche
realisiert werden, die zu einem Objekt das nächstgelegene ermittelt. Statt consistent wird
eine allgemeinere Methode search angeboten, die, je nach Baumtyp, auf vorhandene Ordnungen der Einträge Rücksicht nehmen kann (beispielsweise binäre Suche bei geordneten
Einträgen). Das Knotenlayout ist dazu so zu ändern, dass GiST-Spezialisierungen die
Ordnung der gespeicherten Werte bestimmen können. Statt mit penalty alle Teilbäume
auf Prädikatänderungen beim Einfügen überprüfen zu müssen, kann findMinPen eine
KAPITEL 4. GIST-INDEXE
42
Ordnung ausnutzen, um nur wenige Teilbäume zu überprüfen. insert sorgt für ein der
Ordnung entsprechendes Einfügen neuer Einträge in die Knoten.
Es handelt sich dabei um eine echte Erweiterung in dem Sinne, dass die ursprüngliche
Funktionalität nicht beeinträchtigt wird. So kann man sich für ungeordnete Knoteneinträge auch entscheiden, in search weiterhin alle Einträge auf Konsistenz zu prüfen, die
Einträge in den Knoten beliebig vorzunehmen und weiterhin einen Stack bei der Suche
zu verwenden.
4.2.2
Funktionsübersicht
Die libgist stellt dem Anwender eine einheitliche Schnittstelle zur Verwendung verallgemeinerter Suchbäume zur Verfügung. Durch die Erzeugung eines Objektes der Basisklasse
gist wird ein Sitzungsobjekt erstellt, welches einen generischen verallgemeinerten Suchbaum darstellt. Erst beim Öffnen oder Erzeugen eines Suchbaumes wird die SuchbaumSpezialisierung festgelegt. Dann können Anfragen oder Änderungen ausgeführt werden,
bis der Baum geschlossen wird, und das gist-Objekt damit seine spezielle Ausprägung
wieder verliert. Vor der Zerstörung des Objektes können mehrere Sitzungen stattfinden,
also auch noch weitere, andere Suchbäume geöffnet und verwendet werden. Damit ist es
nicht nötig, Objekte einer festgelegten Spezialisierung zu verwenden, sondern zur Laufzeit
kann eine der implementierten Spezialisierungen ausgewählt werden.
Die typische Verwendung eines GiST-Objektes für einen Anwender läuft folgendermaßen ab: Zunächst wird ein Objekt der Klasse gist initialisiert und dabei der zugehörige
Konstruktor aufgerufen. Mit den Methoden open(Dateiname) oder create(Dateiname,
Spezialisierung) wird ein existierender Suchbaum geladen oder ein neuer, mit der entsprechenden Spezialisierung, erstellt.
Mittels insert(. . .) können jetzt Paare bestehend aus Schlüssel- und Datenelement
in den Baum eingefügt werden (also beispielsweise ein MBR und eine RowID).
Die Suche im Baum verläuft mehrstufig. Bevor der Suchvorgang beginnt, werden noch
zwei weitere Objekte benötigt: Eines vom Typ gist_query_t, das zur Spezifizierung der
Anfrage dient, und ein Iterator, im Datenbank-Kontext auch Cursor genannt, vom Typ
gist_cursor_t, der Informationen zum Baumdurchlauf und der aktuellen Suche speichert. Die Anfragen sind vom verwendeten Baumtyp abhängig, in R*-Bäumen etwa Anfragen auf Überlappung, Schnitt oder Gleichheit mit dem angegebenem Suchprädikat. Die
Methode fetch_init(. . .) initialisiert den Cursor entsprechend der Anfrage. Dabei wird
an Hand der Anfrage die zu verwendende Cursor-Erweiterung ausgewählt. Die Abfrage
des Suchergebnisses wird mit mehrmaligem Aufruf der Methode fetch(. . .) ausgeführt.
fetch() liefert dazu Schlüssel und Datenelement in vorher zu reservierende Speicherbereiche.
Um Einträge aus dem Baum zu entfernen, ist eine Anfrage zu konstruieren, die genau
die zu löschenden Einträge findet. Die Methode remove(Query) löscht alle Einträge des
Baumes, die der Anfrage entsprechen.
Der aktuelle Baumzustand kann jederzeit durch einen Aufruf von flush() mit der zugehörigen Datei synchronisiert werden. Ansonsten geschieht dies spätestens beim Beenden
der Verbindung des GiST-Objektes mit einer Index-Datei durch die Methode close().
KAPITEL 4. GIST-INDEXE
4.2.3
43
Klassenübersicht
Die Kernklasse der libgist-Bibliothek ist die Basisklasse gist, die die Methoden für den
Anwender bereitstellt. Die Bibliothek arbeitet dateibasiert, die verallgemeinerten Suchbäume werden jeweils in einzelnen Dateien abgelegt. Als Schnittstelle zum Dateisystem
existiert eine Klasse gist_file. Sie stellt eine seitenbasierte Verwaltung zur Verfügung
und ermöglicht die Speicherung einiger Meta-Daten in einem Datei-Header (z.B. magicstring, Baum-Spezialisierung, ungenutze Seiten). Damit die Seiten bei mehrfacher Verwendung nicht ständig neu geladen oder geschrieben werden müssen, kann eine festgelegte
Zahl davon im Hauptspeicher verwaltet werden. Der Zugriff darauf erfolgt über eine HashTabelle (gist_htab). Die Größe eines Baumknotens entspricht der einer Speicher-Seite.
Zugriff auf die Seitenstruktur (Seiten-Header, Einträge (slots), Verzeichnis der Einträge)
und zugehörige Management-Funktionen erfolgt über die Klasse gist_p.
Zur Erweiterung des Baumes sind mehrere Klassen als Ausgangspunkte vorgesehen.
gist_ext_t spezifiziert die grundlegende Erweiterungsklasse. Die abstrakten Methoden
(insert, findMinPen, serach, union,. . .) müssen in Unterklassen spezifiziert werden. Diese
Klasse ermöglicht weitgehende Kontrolle über das Knoten-Layout des Baumes.
Sind die Knoten eines Baumes nicht geordnet, so kann die Klasse gist_unordered_t
als Ausgangspunkt gewählt werden. Darin wird ein Interface, wie im original GiSTArtikel ([HNP95]) beschrieben, bereitgestellt. Das Knotenlayout wird dabei von der Klasse gist_unorderedn_t (man beachte das zusätzliche n“), einer Unterklasse von gist_
”
ext_t, bereitgestellt. Zur Erstellung einer neuen (ungeordneten) Baumspezialisierung
werden in einer Unterklasse die abstrakten Methoden aus gist_unordered_t implementiert. Ein Objekt davon wird dann dem Konstruktor des gist_unorderedn_t-Objektes
übergeben, um das komplette Objekt mit den geforderten Knoten-Methoden (nämlich
ungeordnete Speicherung) und GiST-Methoden (consistent, penalty,. . .) zu erhalten. Eine zusätzliche abstrakte Methode in gist_unordered_t ist queryCursor, die zu einer
Suchanfrage (der Klasse gist_query_t) eine passende Cursor-Erweiterung (gist_cursor_
ext_t) angeben muss.
Die Cursor, vom Typ gist_cursor_t, werden genau wie ein gist-Objekt generisch
erzeugt. Erst bei der Verbindung mit einer Suchanfrage wird ein spezieller Cursor, der
vom Typ gist_cursorext_t oder einer Unterklasse dieses Typs ist, ausgewählt und zum
Anfragen von Datensätzen verwendet.
4.2.4
Suchbaumerweiterungen
Für die libgist sind zahlreiche Suchbaum-Spezialisierungen verfügbar und auch in der
Distribution enthalten. Dies umfasst unter anderem B-Bäume für Ganzzahlen und Zeichenketten, sowie R-Bäume, R*-Bäume, SS-Bäume und SR-Bäume für Punkte und/oder
Rechtecke. Als Cursor-Erweiterungen sind eine Prioritäts-Warteschlange und ein lookup
stack enthalten, der als Prioritätswarteschlange mit der Einfügezeit als Priorisierung realisiert ist.
Möchte man einen neuen Suchbaumtyp implementieren, so werden zwei Vorgehensweisen vorgeschlagen:
KAPITEL 4. GIST-INDEXE
44
1. Die Spezialisierung wird aufgeteilt in die Teilbereiche
• Knotenlayout
• abstrakte Basisklasse mit für dieses Knotenlayout spezifischen Methoden
• spezielle Erweiterungsklasse zur Implementierung der Suchbaum-Methoden
Dabei kann für ungeordnete Einträge in den Knoten die Klasse gist_unorderedn_t
als Ausgangsbasis für das Knotenlayout verwendet werden. Die zugehörigen Methoden sind in gist_unordered_t abstrakt deklariert und müssen in einer Unterklasse
definiert werden.
2. Die Spezialisierung wird direkt als Unterklasse der Erweiterungsklasse gist_ext_t
erstellt. Knoten- und datenrelevante Methoden werden in einer gemeinsamen Klasse
beschrieben.
Ein Beispiel für die erste Vorgehensweise sind die R-Bäume und einige verwandte Spezialisierungen (Sphere-Tree, SS-Tree) der libgist-Distribution. Diese verwenden eine gemeinsame Klasse rtbase_ext_t, die in weiteren Unterklassen für den jeweiligen Baumtyp
vervollständigt werden.
Die zweite Vorgehensweise eignet sich besonders für weniger aufwendige Methoden,
wo nicht viele Variationen erwartet werden. Die B-Baum-Spezialisierungen der libgist sind
Beispiele für dieses Verfahren.
Werden Varianten der bereits vorgegebenen Bäume erstellt, so kann dies geschehen,
indem die Methoden einzelner Teil-Klassen eines Baumes in weiteren Unterklassen überschrieben werden.
Die Implementierung des R*-Baumes in der libgist ist in Abbildung 4.2 skizziert.
Dieser Ausschnitt der libgist-Klassenstruktur zeigt, wie eine R*-Baum-Erweiterung als
Erweiterungsobjekt an die Klasse gist angebunden ist. Die abstrakten Methoden sind in
der Abbildung kursiv dargestellt.
Die R*-Baum-Erweiterung überschreibt die Methoden pickSplit() und findMinPen()
der Knotenlayout-Klasse gist_unorderedn_ext_t, die wiederum die abstrakte Erweiterungsklasse gist_ext_t implementiert. In den Methoden der Knotenlayout-Klasse werden Methoden eines Objektes der Klasse gist_unordered_ext_t verwendet. Ein solches Objekt muss daher dem Konstruktor von rstar_ext_t übergeben werden. Konkret
wird bei R*-Bäumen ein Objekt der Klasse rt_ext_t verwendet, einer Unterklasse von
rt_base_ext. Diese Basisklasse definiert die abstrakten Methoden aus gist_unordered_
ext_t und vereint einige Methoden, die in verschiedenen darauf aufbauenden Unterbäumen verwendet werden (R-Bäume, SR-Bäume, SS-Bäume, etc.).
Neue Baumspezialisierungen sind der libgist noch bekannt zu machen (gist_ext.h,
gist_extensions.h). Erst dadurch kann das generische GiST-Objekt die richtigen Unterklassen der Erweiterungsklasse für die gewählte Spezialisierung auswählen. Weitere
Details zur Erstellung neuer Suchbaum-Spezialisierungen oder Cursor-Erweiterungen findet man unter [AK01].
KAPITEL 4. GIST-INDEXE
45
gist_ext_t
+gist_ext_list: gist_ext_t *[]
+myID: enum gist_ext_ids
+myName: char *
+insert()
+remove()
+updateKey()
+findMinPen()
+search()
+getKey()
+pickSplit()
+unionBp()
+queryCursor(): gist_cursorext_t*
gist_unorderedn_ext_t
gist
#_ext: gist_ext_t *
#_file: gist_file
+create()
+open()
+close()
+insert()
+remove()
+fetch_init()
+fetch()
+flush()
+ext: gist_unordered_ext_t &
+insert()
+remove()
+updateKey()
+findMinPen()
+search()
+getKey()
+pickSplit()
+unionBp()
+queryCursor(): gist_cursorext_t *
rstar_ext_t
+ext: rt_ext_t &
+findMinPen()
+pickSplit()
gist_unordered_ext_t
+consistent()
+penalty()
+union_bp()
+pickSplit()
+queryCursor(): gist_cursorext_t *
rtbase_ext_t
+consistent()
+union_bp()
+queryCursor(): gist_cursorext_t *
rt_ext_t
+penalty()
+pickSplit()
Abbildung 4.2: Ausschnitt aus der libgist-Klassenstruktur: R*-Baum-Spezialisierung
4.2.5
Einschränkungen der libgist
Einige Einschränkungen bestehen bei der verwendeten libgist-Version, insbesondere im
Vergleich zu den Vorschlägen der original GiST-Publikation [HNP95]:
• Der Verzweigungsgrad eines Knotens hängt von der Seitengröße (festgelegt durch
die Konstante SM_PAGESIZE) und dem tatsächlichen Platzbedarf der Einträge ab.
Insbesondere bei variabler Schlüssellänge kann die Anzahl der Einträge je Knoten
stark variieren.
• Löschvorgänge werden nicht an Hand des zu löschenden Eintrages, sondern an Hand
einer Suchanfrage durchgeführt. Der Benutzer muss also zum Löschen genau eines
Eintrages eine Such-Anfrage formulieren, die genau diesen Eintrag findet. Ansonsten
werden alle der Anfrage entsprechenden Einträge gelöscht. Dabei darf die Anfrage
nur Operatoren verwenden, die unabhängig von anderen Einträgen auswertbar sind,
also insbesondere keine nearest neighbour -Anfragen, wo erst am Ende der Suche klar
ist, welcher Eintrag die Suchbedingung erfüllt.
Diese Einschränkung hat zur Folge, dass Einträge mit identischen Schlüsseln nicht
einzeln aus dem Baum entfernt werden können. Verschärft wird dieses Problem
durch die Tatsache, dass durch Komprimierung der Schlüssel Duplikate noch wahr-
KAPITEL 4. GIST-INDEXE
46
scheinlicher werden, zumal in einer Datenbank-Relation Duplikate generell erlaubt
sind.
• Werden Einträge aus Blättern gelöscht, so werden die Suchprädikate des Vorgängers
nicht neu berechnet und bleiben dadurch gegebenenfalls unnötig groß.
• Leere Knoten werden nicht gelöscht, sondern verbleiben im Baum. Auch ein Zusammenfassen unterfüllter Knoten wird nicht untersützt. Dies kann nach häufigen
Löschoperationen zu schlechten Anwortzeiten führen, da aufgrund unzureichend gefüllter Knoten unnötig viele Teilbäume expandiert werden müssen.
Kapitel 5
GiST Indexe für Oracle
Oracle 9i bietet als objektrelationale Datenbank die Möglichkeit, benutzerdefinierte Typen und zugehörige Objekte aus bereits existierenden Typen zu erstellen. Die Typen
und Methoden können zu einem Data Cartridge zusammengefasst werden, so dass sie
als Einheit in die Datenbank eingebunden werden können. Einige Methoden können Vergleichsoperationen implementieren, die dem Datenbanksystem als Operatoren bekannt
gemacht werden können.
Ein Beispiel für ein Data Cartridge ist das Spatial Cartridge 1 der Oracle Corporation,
welches die Datenbank um Datentypen für räumliche Daten ergänzt (Punkte, Linienzüge, Polygone, zusammengesetzte Polygone, etc. ) Weiterhin stellt Spatial eine Reihe
von Operatoren zur Selektion (Auswahl von Datensätzen in einem query window ) und
Aggregation (Vereinigung, MBR-Berechnung) dieser Datentypen zur Verfügung. Zur Indexunterstützung einiger Operationen werden R-Bäume und Quadtree-Indexe angeboten.
5.1
Oracle - Extensible Indexing Interface
Um effektiv auf Objekte zugreifen zu können, ist es sinnvoll, passende Indexstrukturen
bereitzustellen. Dies ermöglicht das Extensible Indexing Interface des Oracle Data Cartridge Interface (ODCI), welches dem Benutzer eine Schnittstelle zur Verfügung stellt,
um eigene Datentypen geeignet zu indexieren. Dazu muss der Benutzer eine Reihe vorgegebener Methoden implementieren, die bei einer Anfrage an die Datenbank verwendet
werden, wenn ein unterstützter Operator auf einer indexierten Spalte zur Selektion einzelner Zeilen verwendet wird. Die Schlüssel und RowIDs der Datensätze sollen dabei in
einer geeigneten Datenstruktur gespeichert und schnell wieder abrufbar sein.
Aus Gründen der Konsistenzerhaltung und Transaktionssicherheit wird eine Speicherung der Indexdaten in Tabellen der Datenbank empfohlen. Im Falle eines konkurrierenden Zugriffes zweier Benutzer kann das Datenbanksystem bei externen Speicherstrukturen
keinen kollisionsfreien Zugriff (z.B. während einer Änderung des Indexes) gewährleisten.
Werden Tabellen genutzt, kann die Transaktionsverwaltung der Datenbank genutzt werden, um gleichzeitige Lese- und Schreibversuche zu koordinieren.
1
Produktname: Oracle Spatial, auch einfach Spatial genannt
KAPITEL 5. GIST INDEXE FÜR ORACLE
48
Im Falle einer Rücknahme von Änderungen (rollback) muss auch der zugehörige
Index zurückgesetzt werden. Bei externen Speicherstrukturen sind dazu die Änderungen
zu protokollieren, oder Kopien der Datenstrukturen vor Änderung anzulegen, um wieder
einen konsistenten Zustand herstellen zu können. Einfacher geht dies bei der Nutzung
von Tabellen der Datenbank zur Ablage der Speicherstrukturen, da diese ebenfalls zurückgesetzt werden können.
Die Methoden des Extensible Indexing Interface können in jeder Programmiersprache implementiert werden, die durch die Datenbank unterstützt werden. Somit kommen
PL/SQL, Java und C in Frage, letztere sind als externe Sprachen über PL/SQL einzubinden. Aus Performance-Gründen ist C insbesondere zur Implementierung aufwendigerer
Algorithmen zu empfehlen. C-Programme werden dazu als shared library bereitgestellt,
deren Prozeduren durch einen Erweiterungsprozess (extproc) der Datenbank aufgerufen werden. Damit kommt auch C++ als Programmiersprache in Frage, denn C++Prozeduren können über eine Linker-Anweisung in C-Semantik bekannt gemacht werden.
Vor der Erstellung eines benutzerdefinierten Indexes muss ein Objekttyp erstellt werden, der die vom Indexing Interface geforderten Methoden beinhaltet und der Speicherung des Zustandes zwischen zwei externen Bibliotheks-Aufrufen dient (scan context). Zu
diesem Objekttyp kann ein Indextyp erstellt werden, der spezifiziert, welche Operatoren
durch diesen benutzerdefinierten Index unterstützt werden.
Die Operatoren müssen auch als funktionale Implementierung vorliegen, d.h. auch ohne Indexunterstützung angeboten werden. Ist nur eine indexgestützte Verwendung sinnvoll, so kann die funktionale Implementierung beispielsweise mit einer Fehlermeldung
abbrechen, die den Benutzer zur Erstellung eines Indexes auffordert. Unter gewissen Voraussetzungen ist es allerdings auch möglich, in der funktionalen Implementierung auf den
Index zuzugreifen2 .
Sind diese Vorbereitungen getroffen, so kann ein Index zu einem passenden Attribut
erstellt werden:
create index INDEXNAME on TABELLE(SPALTE)
indextype is INDEXTYP parameters(’PARAMETER’);
5.1.1
Methoden des Extensible Indexing Interface
Bei der Erstellung eines Indexes wird die Methode ODCIIndexCreate(. . .) aufgerufen.
Der Methode wird eine Struktur mit zahlreichen Informationen zu der zu indexierenden
Tabelle, etwaige Parameter, die der Benutzer im SQL-Kommando angegeben hat und
eine Datenbank-Verbindung übergeben. ODCIIndexCreate() muss nun für den Aufbau
der nötigen Indexstrukturen sorgen, wobei es der Implementierung überlassen bleibt, wo
die dabei anfallenden Daten abgelegt werden.
Über die Datenbankverbindung sind Rückrufe (callbacks) an die Datenbank möglich.
Darüber ist eine Speicherung der Indexdaten in einer Tabelle der Datenbank möglich,
ohne sich als externes Programm separat (mit entsprechender Authentifizierung) mit
2
Siehe dazu Seite 7-35 in [O9i-DCDG]: Creating Index-based Functional Implementation“
”
KAPITEL 5. GIST INDEXE FÜR ORACLE
49
der Datenbank verbinden zu müssen. Sollte die zu indexierende Tabelle bereits Einträge
enthalten, so ist es Aufgabe von ODCIIndexCreate() diese über die Datenbankverbindung
abzurufen und in die Indexstruktur einzufügen.
Eine Änderung eines Indexes (alter index . . .) führt zu einem Aufruf der Methode
ODCIIndexAlter(). Hiermit ist es u.a. möglich, einem Index neue Parameter zu übergeben (z.B. einen anderen Speicherort), den Indexnamen zu ändern, oder einen Neuaufbau
des Indexes anzufordern, falls die Qualität des Indexes nach einer längeren Verwendung
nachlässt. Die Methode sollte den Index entsprechend der neuen übergebenden Parameter
ändern, soweit dies unterstützt wird.
Soll ein Index nicht mehr weiter verwendet werden, so wird er mittels drop index . . .
gelöscht. ODCIIndexDrop() ist dafür zuständig, die vom Index genutzten Ressourcen wieder freizugeben.
ODCIIndexCreate
Indexoperationen
ODCIIndexDrop
Abbildung 5.1: Lebenszyklus eines benutzerdefinierten Indexes
Während des laufenden Betriebes können sich die Daten der indexierten Tabelle ändern. Betrifft dies auch die indexierte Spalte, so führt ein Aufruf von insert, update
und delete jeweils zu einem Aufruf von ODCIIndexInsert(), ODCIIndexUpdate() und
ODCIIndexDelete(). Zusätzlich zur RowID werden bei Einfüge- und Änderungsoperationen die neu einzutragenden Werte, bei Änderungs- und Löschoperationen die alten Werte
übergeben.
bis alle Einträge gefunden
ODCIIndexStart
ODCIIndexFetch
ODCIIndexClose
Abbildung 5.2: Methodenaufruf beim Indexzugriff
Die Anfragebearbeitung geschieht, wie in Abbildung 5.2 zu sehen ist, in drei Stufen:
ODCIIndexStart() übergibt man den Operator, der durch den Index unterstützt werden soll, und möglicherweise ein Vergleichsobjekt. Zusätzlich wird ein Vergleichsintervall
(Start- und Stopp-Wert) angegeben, welches beispielsweise eine Zielgröße angeben kann.
Wird ein Index beispielsweise bei einer Anfrage verwendet, um Objekte einer bestimmten Größe (z.B. die Fläche eines Polygones) zu selektieren, so kann diese hier übergeben
werden.
Die Ergebnisse der Indexabfrage bestehen aus den RowIDs der entsprechenden Zeilen
der indexierten Tabelle. Diese werden bei einem Aufruf der Methode ODCIIndexFetch()
jeweils als Menge von Zeigern zurückgeliefert (deren Anzahl ODCIIndexFetch als Parameter angegeben wird). Evtl. muss die Methode mehrmals ausgeführt werden, bis alle
Ergebnisse abgerufen sind.
KAPITEL 5. GIST INDEXE FÜR ORACLE
50
Da zwischen den einzelnen Funktionsaufrufen der Programmfluss zur Datenbank zurückkehrt, ist es notwendig, Informationen zum aktuellen Status einer Anfrage zwischenzuspeichern (sämtliche Informationen zur Operation werden nur ODCIIndexStart() übergeben!). Im Falle einer externen C-Implementierung geschieht dies, indem von der Datenbank (bzw. dem extproc-Prozess) Speicher angefordert wird (OCIMemoryAlloc()),
der zur Ablage des sogenannten scan context dient. ODCIIndexStart() richtet den scan
context ein, indem Speicher für eine Struktur mit allen zu speichernden Informationen
angefordert wird. Diese Speicheradresse wird dann im Objekt gespeichert, welches auch
diese Methoden beinhaltet. ODCIIndexFetch kann damit wieder die Speicherstruktur erhalten und den eigenen Status darin vermerken. Dabei ist es durch Einsatz von Zeigern
in der Speicherstruktur und wiederholtem Aufruf von OCIMemoryAlloc auch möglich,
weiteren Speicher zu alloziieren.
Werden keine weiteren Ergebnisse mehr zurückgeliefert, so soll ODCIIndexClose() für
den Abschluss der Operation sorgen, indem alle verwendeten Ressourcen wieder freigegeben werden.
5.2
OraGIST-Bibliothek
Im Rahmen einer Diplomarbeit ([Lö01]) wurde von Ulf Löckmann eine Bibliothek entwickelt, die es ermöglicht, eine Verbindung der Schnittstellen der libgist und der Datenbank
Oracle (damals in der Version 8i) über das Extensible Indexing Interface zu erstellen.
Damit ist eine Unterstützung verallgemeinerter Suchbäume als Indexierungsstruktur
für benutzerdefinierte Indexe möglich.
5.2.1
Änderungen an der libgist
Um einige der Beschränkungen der libgist zu überwinden, wurden Teile der Bibliothek
geändert, um sie als Erweiterung der Oracle-Datenbank nutzbarer zu machen.
Da es sinnvoll ist, die Speicherstruktur der indexierten Daten in der Datenbank abzulegen, die libgist aber dateibasiert arbeitet, wurde die Klasse gist_file so geändert,
dass nicht Seiten einer Datei verwendet, sondern die Datenbankverbindung zur Ablage
von Speicherseiten genutzt werden kann.
Die in der libgist verwendeten Seiten haben eine feste Länge SM_PAGESIZE. Bei dateibasierter Operation wird aus einer angeforderten Seitennummer eine Position in einer Datei berechnet und ein entsprechend großer Speicherbereich gelesen oder geschrieben. Zur
Verwendung der Datenbank zur Seitenspeicherung wird im Datenbanksystem eine zweistellige Relation erstellt, die als Attribute eine Seitennummer (pageno vom Typ NUMBER)
und einen Speicherbereich zur Aufnahme der Daten besitzt (page: RAW(SM_PAGESIZE)).
Anstelle eines Dateizugriffes wird bei Ablage in der Datenbank in der Klasse gist_file
ein entsprechendes SQL-Kommando zum Lesen oder Schreiben einer Datenseite generiert
und ausgeführt.
Beim Löschen von Einträgen fordert die libgist, dass eine Anfrage formuliert wird,
die die zu löschenden Einträge spezifiziert. Dabei werden alle Einträge gelöscht, deren
KAPITEL 5. GIST INDEXE FÜR ORACLE
51
Schlüssel der Anfrage enstprechen. Um auch einzelne Einträge aus einem Suchbaum entfernen zu können, deren Schlüssel mehrfach vorhanden sind, wurde die libgist dahingehend
geändert, dass beim Löschen auch die RowID, also das zu einem Eintrag gehörende Datenelement, übergeben wird. Damit ist eine eindeutige Identifizierung des zu löschenden
Eintrages möglich, die beim Löschen berücksichtigt wird.
Bei der Suche eines zu löschenden Eintrages wird die formulierte Anfrage verwendet,
um den richtigen Knoten ausfindig zu machen. Zur Suche wird wiederum die zugehörige Cursor-Erweiterung verwendet. Dabei wird aber nicht der Pfad von der Wurzel zu
dem Knoten mit dem zu löschenden Eintrag gespeichert, weswegen die libgist auch den
umgekehrten Weg nicht kennt, um die Prädikate der Vorgängerknoten zu aktualisieren.
Um unnötig große Prädikate zu vermeiden, wurde das Knotenlayout der libgist dahingehend geändert, dass auch Verweise auf die Vorgängerknoten in den Knoten abgelegt
werden. Die Vorgänger können nach einem Löschvorgang gefunden, und die Prädikate
der Nachfolger aktualisiert werden. Dies geschieht in einer neuen Methode _shrink()
der Hauptklasse gist, bis sich im Laufe der Verarbeitung, von den Blättern Richtung
Wurzel fortschreitend, die Prädikate nicht mehr ändern.
Da leere Knoten in der original Implementierung der libgist im Baum verbleiben,
können Löcher“ im verwendeten Speicherbereich entstehen und unnötigen Speicherplatz
”
belegen. Um dies zu vermeiden, wird in _shrink() der Eintrag einer leeren Seite zunächst
aus dem Vorgänger entfernt. Anschließend wird die letzte Speicherseite des Baumes an die
nun freie Seitenposition bewegt und die Datei entsprechend gekürzt (oder die letzte“ Seite
”
in der Datenbank gelöscht). Mit den gespeicherten Verweisen auf den Vorgängerknoten
kann dieser gefunden, und der neue Speicherplatz der ehemals letzten Seite aktualisiert
werden. Dieser Vorgang kann sich, sollten dadurch wiederholt freie Knoten entstehen,
gegebenenfalls bis zur Wurzel fortsetzen.
Des weiteren wurden noch Anpassungen vorgenommen, um die libgist auf dem installierten Linux-System fehlerfrei kompilieren zu können. Gefundene Fehler in der ProgrammLogik wurden behoben. (Nähere Informationen finden sich in Kapitel 7 und Anhang A in
[Lö01].)
5.2.2
Struktur der Implementierung
Die OraGiST-Architektur besteht aus zwei Teilen: Der eine Teil ist unabhängig vom Datentyp und verwendeten Suchbaum. Die OraGiST-Library stellt damit das Bindeglied
zwischen der Schnittstelle der libgist und dem Extensible Indexing Interface dar. Dieser Teil implementiert die Methoden des Indexing Interfaces, in denen die generischen
Indexfunktionen der zugrunde liegenden libgist aufgerufen werden. Auch die Anpassung
der libgist an die Datenhaltung in Tabellen der Datenbank ist der Library-Komponente
zuzurechnen.
Die OraGiST-Toolbox ist dagegen vom Typ der zu indexierenden Objekte abhängig.
Dazu gehört insbesondere auch eine Anpassung der verwendeten Suchbäume an die darin
zu speichernden Schlüssel. Bei der Erstellung einer neuen OraGiST-Spezialisierung wird
der Benutzer durch ein Tool oragist unterstützt. Es handelt sich dabei um ein ShellSkript zur Automatisierung benötigter Vorarbeiten.
KAPITEL 5. GIST INDEXE FÜR ORACLE
52
Abbildung 5.3 gibt einen Überblick über die Struktur der OraGiST und des Zusammenspiels der verwendeten Schnittstellen.
Oracle Datenbank
Methoden−Aufrufe
GiST
Oracle Indexing Interface
1
1
1
GiST−Index−Datei
GiST−Erweiterung
1
gespeichert in
DB−Tabelle
n
1
OraGiST−Bibliothek
OraGiST
Benutzerdef. Indexstruktur
1
1
OraGiST−Erweiterung
+getExtension()
+getQuery()
+needFilter()
+approximate()
n
OraGiST−Toolbox
libgist−library
n
Benutzerdef. Datenbankobjekt
GiST−Eintrag
Abbildung 5.3: Architektur der OraGiST
5.2.3
Die Klasse OraGiST
Die abstrakte Klasse OraGiST stellt die Basisklasse aller mit dieser Bibliothek zu erstellenden Suchbäume dar. OraGiST ist selber eine Unterklasse der gist-Klasse der libgist, stellt
aber zusätzliche Funktionalitäten bereit. Diese bieten eine Schnittstelle zum Extensible
Indexing Interface und dienen dem Aufbau eines Suchbaumes zu einer Datenbankrelation. Dabei benötigte Funktionen, etwa das Auslesen der Tupel einer nichtleeren Tabelle
bei der Indexerstellung, werden bereits teilweise bereitgestellt.
Die wichtigsten implementationsunabhängigen öffentlichen Methoden sind:
ogcreate(): Für den Indexnamen wird ein Tabellenname oder Dateiname von der Spezialisierung erfragt, der bei der Anlage des Suchbaumes mit create() verwendet
wird. Das zu indexierenden Attribute und die zugehörigen RowIDs werden (im Fall
einer nichtleeren Tabelle) ausgelesen, die Schlüssel komprimiert, und die jeweiligen
Paare im Suchbaum abgelegt.
ogdrop(): Löschen des Suchbaumes und der zugehörigen Speicherstruktur.
oginsert(): Speicherung und Komprimierung des Attributes mit der zugehörigen RowID.
KAPITEL 5. GIST INDEXE FÜR ORACLE
53
ogdelete(): Eine Anfrage, die mindestens das zu löschende Element liefert, wird erstellt
und remove() mit der RowID des Elementes übergeben.
ogfetch init(): Initialisierung einer Suche mit einem Aufruf von fetch_init().
ogfetch(): Bis zu der von der Datenbank geforderten Höchstzahl an Antwortsätzen werden Einträge aus dem Suchbaum gelesen (fetch()). Die dabei erhaltenen RowIDs
werden in einer Collection gesammelt. Diese wird dem DB-System zur weiteren
Verarbeitung zurückgegeben.
ogclose(): Der Suchbaum wird über die gist-Methode close() geschlossen.
Zur Verwendung eines GiST-Indexes zur Indexierung eines Datentyps der OracleDatenbank ist eine Unterklasse von OraGiST zu erstellen, die die abstrakten Methoden
dieser Klasse implementiert. Die Unterklasse hängt dabei wesentlich von den folgenden
drei Parametern ab:
1. Von der zu verwendenden Suchbaum-Spezialisierung (R*-Baum, B-Baum,. . .)
2. Vom Datentyp, der dem Suchbaum als Schlüssel dient (Intervalle, Rechtecke, Quader, Kreise,. . .)
3. Vom Datentyp der Datenbank, der durch den Schlüssel dargestellt oder angenähert
werden soll (Polygon, Kreis, Intervall,. . .)
Um auf die Datentypen einzugehen, müssen folglich die datentypabhängigen abstrakten Methoden in OraGiST spezifiziert werden. Dies geschieht durch Definition der folgenden öffentlichen, indextypspezifischen Methoden in einer Unterklasse von OraGiST:
getExt(): Diese Methode soll eine Referenz auf die zu erstellende Suchbaum-Spezialisierung zurückliefern. Dies kann durch Erzeugung eines Objektes des Erweiterungstyps
gist_ext_t oder durch einen Zeiger auf einen entsprechenden Suchbaum geschehen.
(Zur Auswahl eines R-Baumes für Rechtecke beispielsweise: rt_rect_ext)
getMaxKeySize(): Die maximale Größe eines Schlüssels im Suchbaum wird benötigt,
um für einen Aufruf von fetch() ausreichenden Speicherplatz bereitzuhalten. Die
von fetch() ebenfalls benötigte Größe eines Datenelementes ist durch die feste
Länge der RowIDs vorgegeben.
getIdxFileName(): Zum angegebenen Indexnamen soll eine Zeichenkette für einen gültigen Dateinamen erzeugt werden. Üblicherweise gibt man die Konkatenation eines
Verzeichnisses im Dateisystem mit dem Indexnamen zurück.
approximate(): Diese Methode dient der Komprimierung der abzuspeichernden Schlüssel und wird in den Methoden ogcreate() und oginsert() verwendet. Dazu erhält
approximate() das Objekt und eine Datenbankverbindung, die zum vollständigen Abruf komplexer Objekte genutzt werden kann. Zu dem Objekt soll damit ein
für den Suchbaum geeigneter Schlüssel erstellt werden. Im Falle eines GeometrieObjektes kann dies beispielsweise die bounding box sein.
KAPITEL 5. GIST INDEXE FÜR ORACLE
54
getQuery(): Die Suche im Baum muss entsprechend dem verwendeten Operator bei der
Datenbank-Anfrage spezifiziert werden. Dazu ist für die mit dem Index verbundenen
Operatoren eine entsprechende Anfrage an den Suchbaum zu liefern. getQuery()
erhält die anfragespezifischen Parameter, also Suchoperator, Vergleichobjekt und
Ergebnisbereich, und soll dazu ein Objekt vom Typ gist_query_t zurückliefern.
Für R-Bäume kann dies beispielsweise rt_query_t::rt_equal, rt_query_t::rt_
overlap oder rt_query_t::rt_nearest sein.
needVerify(): Wenn die in dem Suchbaum gespeicherten Schlüssel nur Annäherungen
der indexierten Objekte sind (also beispielsweise ein MBR in R-Bäumen), der Baumzugriff daher nur mögliche Kandidaten einer Operation liefert, so soll hier true
zurückgeliefert werden. In einer privaten Methode verify() der Klasse OraGiST
wird dann eine Abfrage an die Datenbank gestellt, die mittels der funktionalen
Implementierung des Operators das Ergebnis für das tatsächliche Objekt in der
Datenbank überprüft. Nur falls verify() ebenfalls true, also Übereinstimmung
bezüglich der Operation liefert, wird die RowID der Ergebnismenge zugefügt.
Ist die Operation allein durch die Anfrage an den Suchbaum auswertbar, so kann
needVerify() false zurückliefern. Die Ergebnisse der Suchbaum-Anfrage finden
sich dann alle in der Ergebnis-Menge wieder.
5.3
Oracle - Pipelined Table Functions
In Oracle 9i ist es nicht möglich, einen Verbund-Index als benutzerdefinierte Indexstruktur
bereitzustellen. Dehalb kann das Oracle Extensible Indexing Interface nicht verwendet
werden, um einen Verbund zu berechnen, der Indexstrukturen für beide Verbundpartner
verwendet. Es wäre zwar möglich, einen zweiten Index bei der Berechnung heranzuziehen,
aber das Indexing Interface erlaubt es nur, eine RowID zurückzugeben.
Es ist also notwendig, eine Methode zu verwenden, die es erlaubt, die RowIDs der Ergebnismenge paarweise zurückzuliefern. Eine offensichtliche Möglichkeit ist die Erstellung
einer Funktion, die die Ergebnistupel in einer zweistelligen Relation ablegt. Dies erfordert
jedoch einen relativ hohen Verwaltungsaufwand, da die RowID-Paare einzeln mit einem
Callback in die Ergebnisrelation der Datenbank eingefügt werden müssen.
Aus Effizienzgründen wurde daher in dieser Arbeit eine andere Vorgehensweise gewählt: Die Verwendung einer Funktion, die eine Kollektion zurückliefert, auf die wie
auf eine Tabelle zugegriffen werden kann. Dies ist durch die Definition einer sogenannten
pipelined table function möglich. (Beschrieben in Kapitel 12 in [O9i-DCDG]). Diese Funktionen stehen im from-Teil einer select-Anweisung. Die zurückgelieferten Zeilen können
wie die Zeilen einer Tabelle weiterverarbeitet werden, so dass weitere Verknüpfungen
damit möglich sind.
Eine Funktion, die eine Kollektion als Rückgabewert besitzt (also ein varray oder
eine nested table) kann mit dem Schlüsselwort PIPELINED deklariert werden. Damit wird
angezeigt, dass die Funktion ihr Funktionsergebnis iterativ zurückliefern kann, statt alle
Zeilen nach der kompletten Berechnung zu übergeben.
KAPITEL 5. GIST INDEXE FÜR ORACLE
55
Pipeline-Funktionen können selber auch Kollektionen als Parameter übergeben werden. Dies geschieht entweder über einen Parameter eines Kollektions-Typs oder mittels
eines REF CURSORs. Dadurch ist es möglich, mehrere Pipeline-Funtionen hintereinanderzuschalten:
select * from TABLE(f(CURSOR(SELECT * FROM TABLE(g()))));
Die Ausgabe der Funktion g() wird dabei nicht erst komplett in einer temporären Tabelle oder einem Cache zwischengespeichert, sondern kann direkt von f() weiterverarbeitet werden. Im Rahmen dieser Arbeit ist dies allerdings nicht vorgesehen. Die PipelineFunktion dient nur als Datenquelle, sie liefert die Row-IDs der Verbundpartner. Zudem
ist die Übergabe eines Cursors an eine extern implementierte Funktion in der aktuellen
Version 9i noch nicht möglich.
Die Implementierung einer Pipeline-Funktion kann auf zwei Arten geschehen: Entweder als native PL/SQL-Funktion, wo das Laufzeitsystem die einzelnen Rückgabewerte
(evtl. zu Blöcken zusammengefasst) sofort nach ihrer Fertigstellung (mit PIPE ROW(Rückgabewert)) weiterleitet, oder man verwendet die Interface-Vorgehensweise, die bei einer Implementierung in einer externen Programmiersprache (C, Java) verwendet werden
muss. Da nur die Interface-Vorgehensweise für diese Arbeit interessant ist, wird nur diese
weiter betrachtet.
Um eine Pipeline-Funktion in der Interface-Variante zu erstellen, muss zuerst ein
Implementierungs-Typ erstellt werden. Dieser objektwertige Typ stellt Speicherplatz zur
Ablage eines Scan-Kontextes zur Verfügung und beinhaltet die Methoden des ODCITableInterfaces:
ODCITableStart(): Diese Methode initialisiert den Scan-Kontext und führt Aktionen
zur Vorbereitung der anschließenden Operationen aus, wie beispielsweise das Parsen
von Parametern oder Öffnen von Dateien.
ODCITableFetch(): Hier werden evtl. eingehende Datensätze verarbeitet und die Ausgaben zu Teil-Kollektionen zusammengestellt. Um nicht zu viele Kontextwechsel zu
haben, wird nicht jede einzelne Ausgabezeile zurückgeliefert, sondern mehrere Zeilen ergeben eine Teilmenge der Ausgabe-Kollektion. Deren maximale Mächtigkeit
wird der Methode zusätzlich zum Scan-Kontext als Parameter übergeben.
Der Scan-Kontext wird benötigt, um die in ODCITableStart angelegten Datenstrukturen verwenden zu können. Im Falle externer Prozeduren ist es damit möglich, den Speicher, der vom extproc-Prozess angefordert wurde oder wird, auch in
nachfolgenden Aufrufen dieser Methode wiederzuverwenden, ohne dass darin gespeicherte Daten zwischen den Kontextwechseln verloren gehen.
ODCITableClose(): Wurden von der Fetch-Methode keine weiteren Datensätze, sondern ein NULL-Wert zurückgeliefert, so wird diese Methode gestartet, um die verwendeten Ressourcen wieder freizugeben.
KAPITEL 5. GIST INDEXE FÜR ORACLE
56
Werden Pipeline-Funktionen im from-Teil einer Selektion angegeben, so wird für jede
dieser Funktionen ein Objekt des zugehörigen Implementierungs-Typs erstellt. In den jeweiligen Objekten können die zu den einzelnen Funktionen gehörenden Scan-Kontexte
abgelegt werden (also beispielsweise Strukturen mit von einem Erweiterungsprozess angeforderten Speicherbereichen), worauf die Methoden des ODCITable-Interfaces dann
zugreifen können. Ist der Programmfluß nach ODCITableClose wieder zur Datenbank
zurückgekehrt, so ist die Pipeline-Funktion beendet, und das zugehörige Objekt kann
zerstört werden.
bis alle Einträge geliefert
ODCITableStart
ODCITableFetch
ODCITableClose
Abbildung 5.4: Methoden des ODCITable-Interfaces
Wie man in Abbildung 5.4 sieht, ähnelt dieses Interface stark dem Methodenaufruf
des Extensible Indexing Interface bei der Abfrage eines Indexes. Doch im Gegensatz zum
Indexing Interface werden hier nicht einzelne RowIDs sondern Kollektionstypen zurückgeliefert, also beispielsweise Mengen von Objekten.
Der Rückgabewert einer Pipeline-Funktion muss dabei aber nicht zur Compile-Zeit
feststehen, sondern kann bei Funktionen, die verschiedene Datentypen zurückliefern sollen, auch erst zur Laufzeit bestimmt werden. Zur Compile-Zeit einer SQL-Anfrage wird
dann die Methode ODCITableDescribe() mit den Parametern der Funktion aufgerufen. Diese sollte dann den Rückgabe-Typ spezifizieren (oder einen undurchsichtigen Typ
(opaque type) liefern, der der Datenbank nicht bekannt ist, aber in anderen Methoden,
die typischerweise auch in externen Sprachen formuliert sind, weiterverarbeitet werden
kann).
In der Regel werden die Rückgabewerte einer Funktionen aber einen vorgegebenen
Typ besitzen, der dann vor der Deklaration einer Pipeline-Funktion definiert wird. Standardtypen und benutzerdefinierte Typen können dann von zugehörigen Operatoren bei
Vergleichen mit den Rückgabewerten herangezogen werden.
Kapitel 6
Entwurf des Verbund-Algorithmus
6.1
Vorüberlegungen
In Kapitel 3 wurden mehrere Algorithmen zur Erstellung eines räumlichen Verbundes
vorgestellt. Die zugrunde liegenden Indexstrukturen und Techniken kann man dabei unterscheiden in die Algorithmen, die den Raum in sich nicht überschneidende Bereiche
teilen (Z-Codes, teilweise Spatial Hash-Join) und eine Zuordnung zwischen den Objekten
und diesen Bereichen herstellen, und in Algorithmen, die die räumliche Lage der Objekte
in einer Baumstruktur speichern (R-Baum, Seeded-Tree), wobei die Koordinaten von Bereichen des Raumes (die sich auch überlappen dürfen) in den Baumknoten als Wegweiser
zu den Knoten mit den Objekten verwendet werden.
Da im Verlauf dieser Diplomarbeit keine komplett neue Indexstruktur zur Indexierung
von benutzerdefinierten Objekten in Oracle erstellt werden sollte sondern eine Erweiterung der bestehenden Index-Implementierung um räumliche Verbunde, wird ein Verbundalgorithmus benötigt, der auf OraGiST aufgesetzt werden kann.
Z-Codes lassen sich zwar in B*-Bäumen abspeichern, die auch von verallgemeinerten
Suchbäumen unterstützt werden, aber sie erlauben kaum Anpassungen. Insbesondere ist
eine Verallgemeinerung auf mehr als zwei Dimensionen schwierig, denn die den Raum
aufteilenden Z-Elemente würden zunehmend ihre Eigenschaft verlieren, einen ähnlichen
Z-Code bei räumlicher Nähe zu haben. Hinzu kommt, dass die Bit-Strings, die die Objekte
beschreiben, sehr viel länger und zahlreicher werden würden. Dies wirkt sich negativ auf
den dazugehörigen Verbundalgorithmus aus, so dass dieser nicht weiter in Frage kommt.
Der Spatial Hash-Join wird besonders für Verbundstrukturen empfohlen, denen kein
Index zugrunde liegt. Doch gerade das Erstellen der Schlüssel (MBRs) zu den Objekten
ist einer der Punkte, der mit am zeitaufwendigsten ist, da bisher keine geeignete Schnittstelle zur Datenbank bereit steht, um große Objektmengen an externe Programme (oder
Bibliotheken) zu liefern. Auch in der OraGiST-Bibliothek müssen die Objekte bei der
Indexerstellung einzeln aus der Datenbank abgerufen werden, was den wesentlichen Zeitfaktor bei der Indexerstellung ausmacht.
Die Verwendung eines vorhandenen Indexes zur Erfassung der Objektbeschreibungen (MBRs) ist eine Möglichkeit, diesen Kostenfaktor zu begrenzen. Doch muss weiter-
KAPITEL 6. ENTWURF DES VERBUND-ALGORITHMUS
58
hin für beide Indexe anschließend eine ähnliche Baumstruktur aufgebaut werden, deren
Objekte dann miteinander verglichen werden. Insbesondere dieses aufwendige Einrichten nur temporär genutzter Speicherstrukturen erscheint im Vergleich zum potentiellen
Performance-Gewinn des Algorithmus zu aufwendig. Für den Fall eines konkurrierenden
Zugriffes (zwei gleichzeitig ablaufende Verbundberechnungen) sollten diese Speicherstrukturen der Verwaltung der Datenbank unterliegen. Doch gerade das Ablegen und Anfordern von Datenseiten in der Datenbank ist ein entscheidender Flaschenhals bezüglich der
Zugriffsgeschwindigkeit.
Seeded Trees scheinen aufgrund ihrer Baumstruktur bestens zur Speicherung in einem
verallgemeinerten Suchbaum geeignet zu sein. Tatsächlich wäre es auch ohne weiteres
möglich, die oberen Ebenen eines Baumes zu kopieren. In die erste Ebene der grown level
könnte man leere Blätter in diesen kopierten Baum einfügen.
Wird jetzt der Baum gefüllt, so würden zuerst diese Blätter entsprechend der Schlüsselinformation der einzufügenden Elemente gesucht und gefüllt. Doch sollte es notwendig
sein, dass ein Knoten geteilt wird, so würde in einem verallgemeinerten Suchbaum das
normale Teilen stattfinden, so dass nicht die für einen Seeded Tree typischen, unterschiedlich hohe R-Teilbäume an die slot-pointer angefügt werden. Statt dessen würde der Baum
normal wachsen, d.h. dass er zur Wurzel hin“ wächst: Knoten werden geteilt, was sich
”
bis zur Wurzel fortsetzen kann und nötigenfalls zu einer neuen Wurzel des Baumes führt.
Dies zerstört aber gerade die gewünschte Eigenschaft, nämlich identische oder zumindest
ähnliche obere Ebenen.
Möchte man trotzdem ein Verhalten wie bei den Seeded Trees erhalten, z.B. kleine GiSTs an die slot-pointer anhängen, so wären sehr starke Änderungen an der doch
recht komplexen GiST-Bibliothek nötig. Insbesondere erwartet bzw. erstellt diese einen
ausgeglichenen Baum, denn die Art des Knotens (interner Knoten mit Prädikaten und
Verweisen auf weitere Seiten oder Blatt mit Prädikaten und Datenelementen) wird anhand der Höhe (level ) im Baum entschieden.
Das parallele Durchsuchen zweier R-Bäume ist dagegen ein relativ einfacher Algorithmus, den man leicht auf andere Bäume übertragen kann.
6.2
Verbundalgorithmen für GiST
Aufgrund der Baumstruktur eines verallgemeinerten Suchbaumes liegt es nahe, für einen
Verbund einen auf Bäumen arbeitenden Algorithmus an die Besonderheiten eines GiST
anzupassen. Am aussichtsreichsten erscheint dabei die für R-Bäume verwendete Methode,
zwei Baumstrukturen parallel zu durchsuchen.
Hierbei wird bei der Auswahl der zu besuchenden Teilbäume beim R-Baum-Verbund
eine nichtleere Schnittmenge der MBRs verwendet. Da in einem GiST auch andere Datentypen indexiert sein können, es sich bei den Schlüsseln damit nicht zwangsläufig um
Rechtecke handeln muss, ist eine andere geeignete Operation bereitzustellen, um herauszufinden, ob sich ein Verbundpaar in den zugehörigen Teilbäumen befinden könnte.
KAPITEL 6. ENTWURF DES VERBUND-ALGORITHMUS
6.2.1
59
Einfacher GiST-Verbund
Eine einfache Variante eines Verbundes zweier GiST-Strukturen leistet folgender Algorithmus:
gist-join1 (A: GiST1-Node, B: GiST2-Node);
FOR (EA ∈ A) DO
FOR (EB ∈ B) DO
IF meta_intersect(EB .pred, EA .pred) THEN
IF ((A is a leaf page) OR (B is a leaf page)) THEN
output(EA , EB )
ELSE
gist-join1(EA .ptr, EB .ptr)
END
END
END
END
END
Wie beim Verbund zweier R-Bäume bewegt sich der Algorithmus parallel durch zwei
Datenstrukturen. Dazu werden alle Einträge EA des einen Baumes A mit den Elementen EB des zweiten Baumes B verglichen. Statt auf eine nichtleere Schnittmenge zweier
Bounding-Boxen zu prüfen, wird hier eine vom Benutzer anzugebende boolsche Funktion meta intersect aufgerufen, die an Hand der Prädikate der Einträge prüft, ob ein
Verbundpaar gefunden werden kann. Ist dies möglich, so werden die möglichen Paare in
output ausgegeben, falls es sich bei einem der Knoten bereits um ein Blatt handelt. Dabei muss ein Teilbaum möglicherweise bis zu den Blättern weiterverfolgt werden. Handelt
es sich nicht um Blätter, so wird der Algorithmus mit den beiden Teilbäumen rekursiv
aufgerufen, die durch die zu den Einträgen gehörenden ptr referenziert werden.
meta intersect kann so gestaltet werden, dass nicht nur Prädikate gleichartiger GiST-Spezialisierungen überprüft werden können, sondern auch verschiedene Datentypen erlaubt sind. Als Beispiel könnte man sich eine Anwendung vorstellen, die zu Fahrzeugen
in regelmäßigen Zeitabständen eine Position abspeichert. Wird diese Kombination aus
Zeitpunkt und Position in einem gemeinsamen Datentyp in der Datenbank gespeichert
und mit einem verallgemeinerten Suchbaum indexiert, so möchte man vielleicht einen
Verbund mit einer ebenfalls gespeichert Landkarte erzeugen. Eine Anfrage wäre dann
beispielsweise: Welche Fahrzeuge sind (auch) auf Autobahnen unterwegs“. Die Schlüs”
sel der Karte bestehen aber vermutlich nur aus Koordinaten, während die Prädikate der
Fahrzeuginformationen Kombinationen aus Koordinate und Zeitkomponente sein könnten. meta intersect braucht aber nur überprüfen, ob sich die Koordinaten-Komponente
eines Fahrzeuges mit denen einer Autobahn schneidet, die Zeit-Information braucht hier
nicht berücksichtigt werden.
KAPITEL 6. ENTWURF DES VERBUND-ALGORITHMUS
6.2.2
60
Zusätzliche Selektionen
Die Beispiel-Anfrage wirft aber gleich eine weitere Frage auf: Wie erhält man die Autobahnen? Angenommen in der Straßenkarte sind alle Straßen und zusätzlich deren Typ
gespeichert. Diese Information gehöre zum Datentyp der Karte und ist auch als Information im GiST der Landkarte gespeichert. Dann wäre es sinnvoll, statt aller Elemente der
Knoten nur diejenigen zu überprüfen, die einer vorherigen Selektion entsprechen. Eine
etwas erweiterte Version eines GiST-Verbundes stellt daher folgender Algorithmus dar:
gist-join2 (A: GiST1-Node, α:Predicate1, B: GiST2-Node, β: Predicate2);
FOR (EA ∈ A) DO
IF consistent1(EA , α) THEN
FOR (EB ∈ B) DO
IF consistent2(EB , β) THEN
IF meta_intersect(EB .pred, EA .pred) THEN
IF ((A is a leaf page) OR (B is a leaf page)) THEN
output(EA , EB )
ELSE
gist-join2(EA .ptr, α, EB .ptr, β)
END
END
···
END
Mit den jeweils zu den GiST-Spezialisierungen gehörenden consistent-Methoden
können dabei Elemente vorselektiert werden, die für den Verbund nicht in Frage kommen.
Wie bei der Suche im GiST besagt ein positiver consistent-Aufruf für ein Element aber
noch nicht zwangsläufig, dass wirklich ein der Anfrage entsprechender Eintrag gefunden
werden muss. Dies ist in output zu berücksichtigen, wo die entsprechende consistentMethode weiter verwendet werden muss, falls man einen Teilbaum weiterverfolgen muss,
und nicht bereits zwei Blätter gefunden wurden.
Während meta intersect für die Beispielanfrage weiterhin nur die Koordinaten-Komponente zu vergleichen braucht, sollte es bei einer entsprechenden Anfrage damit möglich
sein, nur bestimmte Elemente der Bäume zu selektieren. Für die Karte etwa nur bestimmte Straßen, oder bei den Fahrzeug-Informationen nur bestimmte Zeitintervalle.
6.2.3
Verbundalgorithmus für die libgist
Die beiden vorigen Abschnitte zeigen, wie ein Verbund für eine GiST-Struktur rekursiv berechnet werden kann. Im Zusammenhang dieser Arbeit ist es allerdings notwendig,
dass die dabei gefundenen Verbundpaare nicht als Ganzes am Ende des Algorithmus zur
Verfügung stehen, sondern nach und nach abgerufen werden können. Denn nur so kann
das ODCITable Interface ausgenutzt werden, dass bereits Daten an die Datenbank zurückliefert, auch wenn der Verbund noch nicht komplett berechnet ist. Es macht daher
KAPITEL 6. ENTWURF DES VERBUND-ALGORITHMUS
61
Sinn, statt rekursiver Aufrufe und damit der impliziten Verwendung eines Stapelspeichers
(der Rücksprungadressen und Daten der verschachtelten Prozeduraufrufe), eigene Stacks
einzusetzen, auf denen der aktuelle Fortschritt der Suche festgehalten wird. Mittels eigener Stacks ist es auch möglich, die Verbundberechnung zu unterbrechen und später
wieder fortzusetzen, ohne komplizierte Aktionen auszuführen, um eine tiefe Rekursion zu
unterbrechen und dann wieder herzustellen.
Gesucht ist also ein Algorithmus, der einzelne Verbundpaare zurückliefert. Dazu ist
der bisherige Algorithmus aufzuteilen in eine Initialisierung des Baumdurchlaufes und
eine anschließend (gegebenenfalls mehrfach) auszuführenden Prozedur, die einzelne Verbundpaare berechnet und zurückliefert.
join-init (A: GiST1, α:Predicate1, B: GiST2, β: Predicate2);
queryA =construct a query for α and A
queryB =construct a query for beta and B
initialize stackA with A.root()
initialize stackB with B.root()
END
Während der Initialisierungsphase werden für jeden Baum Anfragen erstellt, die später
zum Auffinden der zu verbindenden Elemente des Baumes verwendet werden. Desweiteren
wird jeweils ein Stapelspeicher erstellt und mit dem Wurzelknoten der jeweiligen Bäume
gefüllt. Die Anfragen und Stapelspeicher, sowie Zugriffsstrukturen auf die GiST-Objekte
sollten dabei geeignet gespeichert werden (beispielsweise in einem Objekt, welches diese Prozedur als Methode besitzt), damit sie anschließenden Aufrufen von join-fetch
(ebenfalls als Methode dieses Objektes) zur Verfügung stehen.
join-fetch();
WHILE (NOT (stackA .empty() OR stackB .empty())) DO
IF (stackA .top().isItem() AND stackB .top().isItem()) THEN
RETURN (stackA .pop(), stackB .pop())
ELSE
A=stackA .pop()
B=stackB .pop()
FOR (EA ∈ search(A, queryA )) DO
FOR (EB ∈ search(B, queryB )) DO
IF meta_intersect(EA .pred, EB .pred) THEN
stackA .push(EA )
stackB .push(EB )
END
END
END
END
{ELSE}
KAPITEL 6. ENTWURF DES VERBUND-ALGORITHMUS
62
END
{WHILE}
RETURN EOF
END
Zur Vereinfachung berücksichtigt obiger Algorithmus zunächst wieder nur Bäume mit
der gleichen Baumhöhe, auf unterschiedlich hohe Suchbäume wird am Ende der Beschreibung nochmal kurz gesondert ein.
Am Anfang des Verbundalgorithmus wurde auf beide Stapelspeicher die Wurzel der
jeweiligen Suchbäume geschoben. Zu beachten ist, dass sich auch im Verlauf der Verbundberechnung auf den beiden Stacks (am Ende eines Schleifendurchlauf) immer jeweils
gleich viele Elemente auf den Stapeln befinden, denn eine Pop- oder Push-Operation wird
immer sowohl auf dem einen, als auch auf dem anderen Stapel durchgeführt.
Dieser Teil des Algorithmus arbeitet nun folgendermaßen: join-fetch liefert entweder
ein Paar (EA , EB ) von Verbundelementen oder EOF zurück (4. oder vorletzte Zeile).
Dazu wird zunächst untersucht, ob die Stapel bereits leer sind (eigentlich reicht es hier,
zu überprüfen, ob einer der Stapel leer ist, denn wie bereits erwähnt befinden sich am
Anfang einer Schleife immer gleich viele Elemente auf den Stacks). Ist dies der Fall, so
können keine weiteren Elemente gefunden werden und es wird EOF zurückgegeben.
Ansonsten wird der Typ der obersten Elemente der Stapelspeicher überprüft. Handelt es sich dabei um ein item, also einen Datensatz, oder einen Knoten1 ? Im Falle von
Datensätzen werden die Elemente von den jeweiligen Stapeln entfernt und können zurückgegeben werden; die Prozedur wird damit vorerst beendet. Im anderen Fall werden
sie ebenfalls entfernt, um darauf die Suchbaummethode search(node, query) anzuwenden, die die Menge alle Einträge des Knotens node liefert, die dem Suchprädikat query
entsprechen.
Die Ergebnisse der search-Aufrufe müssen nun jeder-mit-jedem“ mittels meta_
”
intersect verglichen werden. Passen die Einträge zusammen, so werden sie auf die
zugehörigen Stacks geschoben. Innerhalb eines Knotenpaares werden also erst alle Verbundpaare der Nachfolger oder enthaltenen Datenelemente ermittelt und auf den Stacks
abgelegt, statt sofort nach dem Finden eines Eintrages eine Rekursionsstufe weiter zu
gehen. Gefundene Verbundpaare (zwei items) landen daher auch erst auf den Stapeln:
Sie werden erst beim nächsten Durchlauf der WHILE-Schleife ausgegeben.
Handelt es sich um verschieden hohe Bäume, so ist die Suche im Baum nur bei dem
höheren Baum weiterzuführen. Die Einträge müssen aber dennoch mit den items des Baumes mit weniger Ebenen verglichen werden, bis auch beim höheren Baum die Blatt-Ebene
erreicht ist und ebenfalls items bei der Suche gefunden werden. Dazu ist es notwendig, die
item-Einträge bei jedem passenden Paar (wo meta_intersect also true liefert), wieder
auf den Stack zu pushen. Damit wird auch erreicht, dass die Anzahl der auf den beiden
Stapeln gespeicherten Einträge am Ende einer Schleife wieder gleich ist.
1
bei gleich hohen Bäumen ist der Typ des obersten Elementes jeweils gleich
Kapitel 7
JoinGiST
Ziel dieser Arbeit ist es, dem Benutzer eine Klassenstrukur bereitzustellen, die er erweitern
und verwenden kann, um einen Verbund zwischen zwei GiST-Strukturen zu berechnen, die
mit der libgist, bzw. speziell OraGiST erstellt wurden. Dazu muss er in einer Unterklasse
der Erweiterungsklasse einige Methoden implementieren, um auf die eingesetzten GiSTSpezialisierungen einzugehen.
7.1
Struktur
Der Zugriff auf die internen Knoten eines libgist-Suchbaumes kann nicht über die öffentlichen Methoden der Bibliothek geschehen, denn dies ist damit nicht vorgesehen. Um
dennoch auch auf private oder geschützte Methoden und Datenstrukturen zugreifen zu
können, gibt es zwei Alternativen bei der Implementierung des Verbundalgorithmus: Die
Klasse gist wird verändert, oder man erlaubt einer anderen Klasse den Zugriff auf die
Interna der Klasse gist.
Bei der ersten Variante wären umfangreiche Änderungen oder Ergänzungen der gistMethoden nötig. Um auf zwei Bäumen arbeiten zu können, wäre es zudem notwendig, zahlreiche Datenstrukturen für dieses doppelte Verwendung hinzuzufügen. Zusätzlich
würde eine starke Verwebung der Komponenten ein späteres Aktualisieren auf neue Versionen der libgist erschweren.
Daher wurde im Rahmen dieser Diplomarbeit der zweite Weg eingeschlagen, nämlich
eine eigenständige Klasse erstellt, die auf internen Strukturen der gist-Objekte zugreifen
darf. C++ ermöglicht dies, indem zwei Klassen als befreundet deklariert werden. Dazu
sind nur zwei weitere Zeilen im Quellcode der GiST-Bibliothek notwendig: In der HeaderDatei gist.h macht class JoinGiST den Namen der anderen Klasse bekannt, friend
class JoinGiST im Rumpf der gist-Klassen-Deklaration erlaubt der Klasse JoinGiST
den Zugriff auf interne Komponenten dieser Klasse.
Da die Eigenschaft eine befreundete Klasse zu sein nicht vererbbar ist, ist es nicht
möglich, weitere Unterklassen der Klasse JoinGiST zu erstellen, ohne die FreundschaftsEigenschaft und damit den uneingeschränkten Zugriff auf gist-Komponenten zu verlieren. Die Anpassung an die zu verbindenden Suchbäume muss daher in einer Erweite-
KAPITEL 7. JOINGIST
64
rungsklasse JoinGiST_ext_t vorgenommen werden. Die virtuellen Methoden der Erweiterungsklasse können in Unterklassen spezifiziert werden. Ein Objekt dieser Unterklassen
ist dann dem JoinGiST-Objekt zu übergeben, so dass dieses dessen spezialisierte Methoden verwenden kann.
Das JoinGiST-Objekt benötigt weiterhin Informationen über die zu verwendenden Indexdatensätze, Tabellen und Attribute. Diese werden in der Klasse JoinGiST_parameters
gesammelt und teilweise verarbeitet.
1
JoinGiST
−joinext: JoinGiST_ext_t *
−parameters: JoinGiST_parameters *
−dbh: DBConnectionHandle
−gist1: gist *
−gist2: gist *
−query1: gist_query_t *
−query2: gist_query_t *
+join_start(): int
+join_fetch(rows:int): int
−double_fetch(...): rc_t
1
1
2
gist
#_ext: gist_ext_t *
#_isOpen: bool
#_file: gist_file
+create()
+open()
+close()
+flush()
+insert()
+remove()
+fetch_init()
+fetch()
+isEmpty()
+extension(): gist_extension_t *
JoinGiST_ext_t
+meta_intersect(key1,isLeaf1:bool,...): bool
+getLeftIdxFileName(idxname:char *): char *
+getRightIdxFileName(idxname:char *): char *
+getLeftQuery(selection:string): gist_query_t *
+getRightQuery(selection:string): gist_query_t *
1
JoinGiST_parameters
#op: string *
#tablename1: string *
#tablename2: string *
#selection1: string *
#selection2: string *
#indexname1: string *
#indexname2: string *
#dbh: DBConnectionHandle
+getSpecialization(out spec1:string *&,
out spec2:string *&): bool
+getOperator(): string *
+getLeftIndexname(): string *
+getRightIndexname(): string *
+getLeftSelection(): string *
+getRightSelection(): string *
+getLeftTablename(): string *
+getRightTablename(): string *
+getLeftColumnname(): string *
+getRightColumnname(): string *
Abbildung 7.1: Ausschnitt der JoinGiST-Klassenstruktur
Bei der verwendeten gist-Klasse handelt es sich um die im Rahmen von OraGiST
erweiterte Variante, die ihre Suchbäume in der Oracle-Datenbank abspeichern kann.
7.2
7.2.1
Methoden der JoinGiST-Klassen
JoinGiST parameters
Die Klasse JoinGiST_parameters speichert die Optionen, die der Start-Funktion des
ODCITable-Interface übergeben werden. Außerdem werden in dieser Klasse die in der
Datenbank gespeicherten Parameter zu den Indexdatensätzen abgefragt. Die öffentlichen
Methoden dieser Klasse sind:
JoinGiST parameters(): Der Konstruktor der Parameter-Klasse erhält erhält sämtliche Parameter, die der Benutzer beim Aufruf der Verbund-Funktion angibt. Dieses
werden der externen Prozedur als C-Zeichenketten (char *) übergeben. Im einzelnen handelt sich sich dabei um:
KAPITEL 7. JOINGIST
65
• operator: Die Verbundoperation, die vom Benutzer gewünscht wird. Diese wird
lediglich in einer C++ Zeichenkette (string *) abgelegt
• table1, table2: Die Tabellen- und Attributbezeichner werden zusammen in einer Zeichenkette übergeben. Die geschützte Prozedur set_SchemaTableColumn
wird verwendet, um diese in die einzelnen Bestandteile zu zerlegen und separat
abzuspeichern.
• selection1, selection2: Die Selektionen werden, falls sie angegeben sind, unverarbeitet in der Klasse abgelegt.
• additional: Dieser Parameter kann zusätzliche Informationen beinhalten und
wird ebenfalls unverarbeitet abgelegt (z.B. wäre die Angabe einer Log-Datei
denkbar).
Zusätlich wird noch ein Datenbankverbindung und jeweils ein Bezeichner für den
Besitzer der Indexdateien gespeichert.
getSpecialization(): Diese Methode prüft zuerst, ob die Parameter der im Konstruktor angegebenen Tabellen schon abgefragt wurden. Ist dies der Fall, so wurde
dabei auch die Bezeichnung der Indexspezialisierung abgerufen, andernfalls wird
check_dba_data() aufgerufen. Die Rückgabe dieser Bezeichner geschieht über zwei
String-Zeiger-Referenzen die als Parameter erwartet werden. Es wird keine Kopie
erstellt, der Speicherplatz der Strings darf daher nicht freigegeben werden (dies
geschieht im Destruktor).
getLeftIndexname(): Hier wird ebenfalls erst überprüft, ob die Datenbank schon abgefragt wurde (ansonsten wird dies getan). Der Indexname, der zur linken Tabelle
gehört, wird dann als C-Zeichenkette zurückgegeben.
getRightIndexname(): Macht dasselbe - für die rechte Tabelle.
isLeftOratab(), isRightOratab(): geben den boolschen Wert zurück, ob die entsprechende Indexdatei in der Datenbank gespeichert ist. Dies wird (wie in OraGiST)
erkannt, indem der PARAMETER-Eintrag des Indexes auf die Zeichenkette " loc=f"
überprüft wird.
getLeftSelection(), getRightSelection(), getLeftTablename(), getRightTable
name(), getLeftColumnname() und getRightColumnname() geben jeweils
Zeiger auf die zugehörigen Strings zurück.
˜JoinGiST parameters(): Der Destruktor gibt die verwendeten Speicherbereiche wieder frei. (Da dies die übliche Aufgabe eines Destruktors ist, wird dies bei den anderen
Komponenten der JoinGiST-Klassenstruktur nicht weiter beschrieben.)
Zusätzlich sind noch einige nichtöffentliche Methoden enthalten. Diese dienen der Abfrage der Tabellen ALL_INDEXES und ALL_IND_COLUMNS der Datenbank, wo insbesondere
KAPITEL 7. JOINGIST
66
die Spalte PARAMETERS interessiert. Denn darin stecken die Informationen, welche Spezialisierung der Index verwendet, und ob er in der Datenbank oder einer Datei gespeichert
ist.
check one dba data(): Die Methode ruft die Index-Daten zu einer der beiden Tabellen
ab, indem eine Anfrage an die Datenbank formuliert und ausgeführt wird. Die erhaltenen Werte werden im Objekt gespeichert, so dass sie nicht nochmals abgerufen
werden müssen.
check dba data(): Durch zweifachen Aufruf von check_one_dba_data werden die Daten zu beiden Indexen abgefragt.
set SchemaTableColumn(): Die table-Parameter enthalten sowohl Angaben zu den
Tabellen, als auch den Spalten, für die ein Index existieren soll. Diese Daten werden
hier getrennt, um sie anschließend in den entsprechenden Variablen abzulegen.
7.2.2
JoinGiST ext t
Die Erweiterungs-Klasse JoinGiST_ext_t dient als Basisklasse für Erweiterungsklassen,
die der Anpassung an die zu verbindenden Bäume dienen. Zu einer Kombination zweier
OraGiST-Suchbäume muss jeweils eine Erweiterungsklasse erstellt werden, um auf die
in den Bäumen gespeicherten Datenstrukturen (und die zugrunde liegenden Suchbäume) einzugehen. Sämtliche Methoden dieser Klasse sind lediglich abstrakt deklariert und
müssen noch in einer Unterklasse definiert werden. Die öffentlichen Methoden sind:
setOperator: Dieser boolschen Methode wird der Verbundoperator (als String) übergeben. Diese sollte hier nicht einfach abgelegt werden, sondern schon verarbeitet
und in einer internen Darstellung gespeichert werden. Bei erfolgreicher Verarbeitung wird true als Rückgabewert erwartet, wird keine Operator im String erkannt,
liefert man false, um einen Fehler zu signalisieren.
getLeftIdxFileName(): Zu dem Parameter idxname vom Typ char * wird ein gültiger
Name im Dateisystem generiert, unter dem der Index abgespeichert ist. Diese Funktion muss auch (ohne Left“) in den Unterklassen von OraGiST angegeben werden,
”
der Rumpf dieser Prozedur kann daher einfach von der zu unterstützenden Spezialisierung übernommen werden. Der Dateiname wird ebenfalls als C-Zeichenkette
(char *) zurückgegeben.
getRightIdxFileName(): Für einen anderen Suchbaum könnte der Pfad zu einer Indexdatei unterschiedlich sein, daher muss er ebenfalls abgefragt werden.
getLeftMaxKeySize(), getRightMaxKeySize(): Die maximale Schlüssellänge, wie
sie ebenfalls in den OraGiST-Spezialisierungen angegeben sind.
getLeftQuery(), getRightQuery(): Diesen Methoden wird jeweils ein Zeiger auf eine
C++ -Zeichenkette übergeben, die eine Selektion beschreibt. Dabei ist das Format,
KAPITEL 7. JOINGIST
67
dass zur Spezifizierung dieser Selektion verwendet wird, demjenigen überlassen, der
diese Methoden implementiert - es wird lediglich eine Vorgabe gemacht: Handelt es
sich um einen NULL-Zeiger, so soll eine Abfrage erstellt werden, die den ganzen Baum
findet. (Bei den R-Baum-Derivaten der libgist erreicht man dies, indem man als
Anfrage-Operator rt_nooper angibt.) Aufgabe ist es nun, den String zu verarbeiten
und eine Anfrage vom Typ gist_query_t * zurückzuliefern.
meta intersect(): Diese Methode implementiert den Vergleich der Schlüssel der beiden
Bäume. Dazu wird der boolschen Methode jeweils ein Zeiger auf einen Schlüssel
und jeweils die Information, ob es sich um einen Schlüssel eines Blattes handelt
übergeben, denn in einigen Bäumen unterscheiden sich die Schlüssel der internen
Knoten von denen in den Blättern. Anhand dieser Informationen und des im Objekt gespeicherten Verbundoperators wird ein Vergleich der Schlüssel vorgenommen.
Kommen die Datenelemente, die zu den Schlüsseln gehören, als Verbundpartner in
Frage, bzw. könnten sich unter zugehörigen Teilbäumen Verbundpartner finden, so
wird true zurückgegeben. Entsprechen zwei Datenelemente in Blätter nicht dem
Verbundoperator oder sind Verbundpartner in zwei Teilbäumen ausgeschlossen, so
soll die Methode false liefern.
Die Zeiger auf die Schlüssel sind typlos (bzw. vom Typ void *), der Benutzer sollte
anhand der verwendeten Spezialisierung wissen, wie die Schlüssel in den Knoten des
Suchbaumes abgelegt sind. Nach einem entsprechenden Cast (auf eine entsprechenden Speicherstrukturen) kann dann auf die Komponenten der Schlüssel zugegriffen
werden.
7.2.3
JoinGiST
Die Klasse JoinGiST ist die Hauptklasse der JoinGiST-Strukur. In ihr wird der eigentliche
Verbund der Indexdatensätze berechnet. Daher ist es auch notwendig, dort die erforderlichen Datenstrukturen zusammenzufassen. Diese Klasse ist in der Klasse gist als friend
eingetragen, damit auf deren internen Datenstrukturen zugegriffen werden kann. Da durch
diese Klasse für den Endanwender aber kein unkontrollierter Zugriff auf private Elemente
der Klasse gist möglich ist, sondern lediglich einige zusätzliche Methoden bereitgestellt
werden, ist JoinGiST als Erweiterung der Zugriffsmöglichkeiten auf GiST-Objekte anzusehen, nicht als Bruch in der Kapselung der Datenstrukturen.
JoinGiST(): Dem Konstruktor wird neben der Datenbankverbindung und dem Parameter-Objekt ein Objekt vom Typ JoinGiST_ext_t * übergeben und im Objekt
abgelegt.
join start(): Diese Methode sorgt für die Vorbereitung des Verbundes. Dazu sind die
Indexnamen und ihre Speicherorte abzufragen. Zwei neue gist-Objekte werden
erstellt und die Indexstrukturen geöffnet. Von der Erweiterungsklasse werden zwei
Abfragen (gist_query_t) an die Suchbäume angefordert, wobei evtl. angegebene
KAPITEL 7. JOINGIST
68
Selektions-Parameter berücksichtigt werden müssen. Rückgabewert ist ein FehlerCode, der angibt, ob alles bei den Vorbereitungen geklappt hat oder ein Fehler
vorliegt.
join fetch(): Diese Methode liefert eine Anzahl an Verbundpaaren in einem Kollektionstyp zurück. Dazu erhält sie neben dem Zeiger auf den anzulegenden Kollektionstyp (und einem Indikator, der angibt, ob es sich dabei um einen NULL-Wert handelt,
die Kollektion also keine Elemente enthält) einen Wert, der angibt, wie viele Paare
angefordert werden.
In dieser Methode wird die private Funktion double_fetch() verwendet, um die
beiden Indexstrukturen parallel zu durchsuchen. Die beiden RowIDs die dabei zurückgeliefert werden, werden mittels der Methode return_results() der Ausgabekollektion zugefügt. Diese geschieht mehrfach, bis die erforderliche Anzahl an
Verbundpaaren gefunden und zur Ausgabe vorbereitet wurde, oder bis keine weiteren Verbundpaare mehr geliefert werden, die Suche also beendet ist.
Neben einigen kleineren privaten Methoden, die jeweils Teilaufgaben übernehmen (z.B.
die Erstellung der gist-Objekte oder das Laden der Datensätze), sind noch die folgenden
privaten Methoden interessant:
double fetch() Diese Methode implementiert den eigentlichen Verbund-Algorithmus.
Dazu wurden die Methoden fetch (und _fetch) der Klasse gist so angepasst,
dass sie nicht nur auf einem gist-Objekt arbeiteten, sondern auf zweien. In dieser Methode werden daher die einzelnen Knoten der beiden Bäume besucht und
die Einträge bestimmt, die der Anfrage (gist_query_t) entsprechen. Anstatt die
qualifizierten Einträge der einzelnen Indexe einfach auf die zugehörigen Stapelspeicher zu verschieben, wird hier aber erst ein Vergleich der Schlüssel aller gefundenen
Einträge des einen Baumes mit den Schlüsseln der Einträgen des anderen Baumes
vorgenommen (mittels meta_intersect der Erweiterungs-Klasse). Die dabei gefundenen Paare werden dann parallel auf die Stapelspeichern geschrieben. Da die
Operationen auf den Stacks immer parallel stattfinden, werden sie dort auch wieder
zusammen abgerufen. Sollten sich im Laufe dieses Prozesses zwei Dateneinträge auf
den Stapeln befinden, so ist ein Paar gefunden. Die obersten Einträge werden daher
von den beiden Stacks entfernt und die zugehörigen Schlüssel und RowIDs werden
zurückgegeben. Der aktuelle Fortschritt des Baumdurchlaufes bleibt dabei erhalten,
da er sich aus den auf den Stacks gespeicherten Werten ergibt. Die Stapel gehören
zu den gist-Objekten und werden daher nicht gelöscht, sondern bleiben bis zum
nächsten Aufruf von double_fetch() unverändert.
Der Methode werden zahlreiche Parameter übergeben (jeweils für jeden Baum:
gist-Objekt, Cursor, Schlüssel-Zeiger, Schlüssel-Länge, Daten-Zeiger, Daten-Länge, eof-Indikator), die größtenteils der Ausgabe der gefundenen Datensätze dienen.
return results(): Dieser Methode werden zwei Zeiger auf die zurückzuliefernden RowIDs (die als char * gespeichert sind) übergeben. Diese werden in einen String-Typ
KAPITEL 7. JOINGIST
69
der Datenbank umgewandelt und dem jeweiligen Teilobjekt (join_result_type.
left oder join_result_type.right) der Ergebnis-Kollektion zugefügt.
7.2.4
odci2join - Schnittstelle zwischen JoinGiST und Oracle
JoinGiST ist als objektorientierte Bibliothek konzipiert und in C++ implementiert. Um
die bereitgestellte Funktionalität mit der Datenbank verwenden zu können, ist es notwendig eine shared library zu erstellen, deren vom extproc-Prozess aufzurufenden Prozeduren
als extern "C" deklariert sind. Diese Prozeduren werden vom Linker entsprechend den
C Funktionsaufruf-Konventionen in der Bibliothek erstellt.
Die C-Prozeduren und auch ein Teil der eigentlichen Programmlogik befinden sich
in der Datei odci2join.cc. Hier werden die externen Prozeduren definiert, die vom
ODCITable-Interface aufgerufen werden. Die C-Prozeduren ODCITableFetch und ODCI
TableClose werden in den gleichnamigen Methoden des Table-Interface aufgerufen.
Um eine unterschiedliche Anzahl an Parametern zu unterstützen, ist in der InterfaceImplementierung die Methode ODCITableStart mehrfach überladen. Es wurden drei
PL/SQL-Funktionen (join3, join5 und join6) erstellt, die diese Interface-Implementierung verwenden. Je nach Parameterzahl wird eine der ODCITableStart-Methoden
aufgerufen, die wiederum eine der als extern deklarierten Prozeduren ODCITableStart_3,
ODCITableStart_5 oder ODCITableStart_6 der JoinGiST-Bibliothek aufrufen (diese können nicht überladen werden, da dies nicht der C-Konvention eines Funktionsaufrufes entspricht). Die C-Funktionen rufen wiederum die C++ Prozedur ODCITableStartCPP auf.
Diese wird nur einmal benötigt, da sie als polymorphe Prozedur implementiert ist. (Einsetzen von NULL-Werten für nicht angegebene Parameter.)
Folgendes leisten die Funktionen in odci2join.cc
ODCITableStartCPP: Die Datenbankverbindung wird initialisiert und der ScanKontext eingerichtet. Anschließend wird ein neues Objekt der Klasse JoinGiST_
parameters erstellt und dessen Methode getSpecialization verwendet, um die
Indextypen der zu verbindenden Bäume festzustellen. Anhand dieser Informationen wird das zugehörige Objekt vom Typ JoinGiST_ext_t ausgewählt, erstellt
und dem Konstruktor des zu erstellenden JoinGiST-Objektes zusammen mit dem
Parameter-Objekt übergeben. Die Methode start() des JoinGiST-Objektes bereitet dieses schließlich auf den Verbund vor.
ODCITableFetch: Die Datenbankverbindung wird initialisiert und der Scan-Kontext
ausgelesen, um die damit gespeicherten Informationen wiederherzugestellen. Anschließend kann die angeforderte Anzahl an Datensätzen über die Methode join_
fetch des JoinGiST-Objektes angefordert werden.
ODCITableClose: Die Datenbankverbindung wird initialisiert und der Scan-Kontext
ausgelesen. Erst dann hat man Zugriff auf das JoinGiST-Objekt - um es zu zerstören
und damit die belegten Ressourcen wieder freizugeben.
KAPITEL 7. JOINGIST
7.3
Einschränkungen
7.3.1
Cursorerweiterung
70
Bezüglich der verwendbaren Suchbaumerweiterungen gibt es eine Einschränkung: Es werden nur Suchbaum-Erweiterungen (bzw. zugehörige Anfragen) unterstützt, die die lookup
stack -Cursorerweiterung verwenden. Die Verwendung der priority queue-Erweiterung ist
damit ausgeschlossen. Dies hat zur Folge, dass keine nearest neighbour -Verbünde möglich
sind.
Da die exakte Berechnung des nächsten Nachbarn eines Objektes aber mit Indexen, die
die MBR des Objektes als Schlüssel verwenden, nicht sicher möglich ist, sollte dies keine
wesentliche Einschränkung darstellen. Üblicherweise werden bei der indexunterstützten
nearest neighbour -Suche die besten n Objekte zurückgeliefert. Als Beispiel, wo dies nicht
B
C
A
D
F
E
Abbildung 7.2: Nearest neighbour Suche
zum gewünschten Erfolg führt, betrachte man Abbildung 7.2. Werden nur die 4 nächsten
Objekte zum Punkt A abgefragt, so liefert der Index lediglich die Objekte B, C, D und E,
denn die MBRs (rot) der Objekte, die dem Index als Schlüssel dienen, liegen am inneren
Kreis und sind A damit am nächsten. Die tatsächlichen Geometrien dieser Polygone sind
dem Index nicht bekannt. Daher weiß er auch nicht, dass das Rechteck F dem Punkt A
eigentlich am nächsten ist.
Eine exakte Berechnung der vier aussichtsreichsten Kandidaten wäre daher nur möglich, wenn die tatsächlichen Geometrien aller Objekte, die sich im äußeren Kreis (also
dem die vier Geometrien umschließenden Kreis) befinden, von der Datenbank abgefragt
und bei der nearest neighbour -Suche verwendet werden.
7.3.2
Compiler
Derzeit ist die libgist-Bibliothek noch nicht an den aktuellen GNU-C-Compiler angepasst.
Die Compiler der 3.x-Reihe verlangen eine Anpassung an die neuen C++-Header, sowie
eine damit einhergehende Nutzung des std::-Namespaces (oder der Angabe von using
namespace std;) in allen Programmteilen. Daher muss das Paket mit dem alten Compiler
der Version 2.95.3 kompiliert werden.
KAPITEL 7. JOINGIST
71
Der C++ -Compiler g++ dieser alten Version hat allerdings Probleme bei der Ausnahmebehandlung im Zusammenhang mit großen Projekten. Löst man in einem try-Block
eine Ausnahme aus (mit throw), so landet man nicht im zugehörigen catch-Block, sondern dass Programm springt an eine zufällige“ Stelle (und stürzt ab).
”
Daher sollte die ansonsten zu empfehlende Verwendung der C++ -Ausnahmebehandlung
mit dieser Compilerversion auch nicht in Unterklasser der JoinGiST-Erweiterungsklasse
verwendet werden.
7.3.3
Speicherort der Indexdaten
JoinGiST verwendet die Index-Daten von OraGiST und ist damit bei konkurrierendem
Zugriff auf diese Datensätzen mit den gleichen Problemen konfrontiert. Insbesondere bei
einer Ablage im Dateisystem besteht kein Schutz, um eine Änderung des Datenbestandes
durch einen anderen Prozess zu unterbinden.
Daher ist es dringend zu empfehlen, die Daten in einer Tabelle der Datenbank abzulegen, indem bei der Indexerstellung der Parameter "loc=db" angegeben wird. Dann
garantiert die Datenbank, dass sich die Sicht auf die Daten für die Dauer des Statements
nicht verändert, auch wenn andere Operationen schreibend auf die Datensätze zugreifen.
Sollte dies in gleichen Statement geschehen, so kann es aber zu ein
Kapitel 8
Anwendung und Performance
8.1
8.1.1
Anwendung
Formulierung von Anfragen
Um eine Verbundanfrage zu initiieren, wird die Verbundfunktion mit den dazu erforderlichen Parametern (die vom Typ varchar2 sind) aufgerufen. Möchte man keine Selektionen
verwenden, so verwendet man join3. Diese Funktion erwartet nur drei Parameter: Der
Verbundoperator und die beiden Tabelle (mit dem zugehörigen, im Index erfassten Attribut). Ein Aufruf geschieht dann nach folgendem Muster:
select * from TABLE(join3(’operator’,
’tabelle1(attribut1)’, ’tabelle2(attribut2)’));
Dabei dürfen zwischen den ’-Zeichen der Tabellenbezeichner keine unnötigen Leerzeichen
vorkommen. Optional kann vor dem Tabellennamen ein Schema angegeben werden, gefolgt von einem Punkt ".". Bis zur öffnenden Klammer kommt der Tabellenname und
zwischen den Klammern steht die bei der Indexerstellung angegebene Spalte. Der Operator kann eine beliebige Zeichenkette sein, die allerdings von der verwendeten Unterklasse
von JoinGiST_ext_t erkannt werden muss. Es steht also dem Benutzer bei der Implementierung seiner Erweiterung frei, welche Operationen unterstützt werden und wie diese
ausgewählt werden. JoinGiST selber verwendet den Operator nicht.
Soll beim Indexzugriff gleich eine Selektion berücksichtigt werden, so verwendet man
join5, mit fünf Parametern:
select * from TABLE(join5(’operator’,
’tabelle1(attribut1)’, ’tabelle2(attribut2)’,
’selection1’, ’selection2’));
Die selection“-Einträge müssen dabei ebenfalls für das Erweiterungs-Objekt Sinn erge”
ben, so dass daraus eine Suchbaum-Anfrage erstellt werden kann.
KAPITEL 8. ANWENDUNG UND PERFORMANCE
8.1.2
73
Weitere Verbunde
Die join-Funktionen liefern über das ODCITable-Interface jeweils Paare von RowIDs
zurück, die das Ergebnis der ersten Filterstufe repräsentieren. Die Rückgabe besteht aus
einem eigenständigen Typ JOIN_RESULT_TYPE mit den Komponenten LEFT und RIGHT,
vom Typ VARCHAR2, in denen die RowIDs als String stehen. Diese können wie ganz
normale Attribute einer Tabelle für weitere Verknüpfungen herangezogen werden.
select L.attribut3, R.attribut5 from tabelle1 L, tabelle2 R,
TABLE(join5(’operator’,
’tabelle1(attribut1), tabelle2(attribut2),
’selection1’ ,’selection2’)) J
where L.ROWID=J.LEFT and R.ROWID=J.RIGHT
and L.attribut3 > 100
and plsqlOperator(L.attribut1, R.attribut2) = ’TRUE’;
Dies macht für die zurückgegebenen RowIDs natürlich nur Sinn, wenn sie mit der
Pseudo-Spalte ROWID der zugehörigen Tabellen verglichen werden.
Im letzen Beispiel könnte plsqlOperator beispielsweise der Durchführung der zweiten Filterstufe eines Verbundes dienen. Sind nämlich noch weitere zusätzliche Selektionen
vorhanden (wie hier mit L.attribut3 > 100, so macht es keinen Sinn, die zweite Filterstufe schon in der JoinGiST-Bibliothek auszuführen. Denn der Index wird ja gerade
verwendet, um teure“ Operationen mit den tatsächlichen Objekten zu vermeiden. Daher
”
ist es sinnvoll, diese erst zu anzuwenden, wenn möglichst viele Objekte aussortiert wurden. Vorraussetzung ist dabei natürlich, dass der Optimierer der Datenbank die Kosten
eines Operatoraufrufes richtig einschätzt und den Verbund in der richtigen Reihenfolge
durchführt.
Zusätzlich gibt es noch eine Funktion join6, mit einem weiteren Parameter additional,
der derzeit nicht genutzt wird, aber beispielsweise zur Angabe zusätzlicher Optionen
verwendet werden könnte. Denkbar wäre beispielsweise die Angabe einer Log-Datei oder
weiterer Optionen an JoinGiST oder die Erweiterungsklasse.
8.2
Praktisches Beispiel mit Performance
Um das Abschneiden des Verbundalgorithmus zu testen wurden zunächst zwei Tabellen
erstellt, zu denen mit OraGiST jeweils eine Indexstruktur aufgebaut wurde.
Der eine Datensatz, NENNDORF enthält 2655 Objekte, zumeist Linienzüge oder Polygone, die einen Ausschnitt aus einer Karte repräsentieren. Der andere Datensatz RECHTECKE
besteht aus 25000 Rechtecken, die dieses Kartenmaterial teilweise überlagern. Die Rechtecke sind in regelmäßigen Abständen über dem gleichen Koordinaten-Raum angelegt,
wobei aber einige mehrfach vorhanden sind.
Die Indexdatensätze werden in der Datenbank abgespeichert, wie dies allgemein empfohlen wird.
KAPITEL 8. ANWENDUNG UND PERFORMANCE
OraGiST
Oracle Spatial
rstar rect ext
R-Baum
74
Anzahl gefundener
Überschneidungen
Anlegen des Indexes
zu NENNDORF
8.3s
2.2s
(Anzahl Elemente)
2655
Anlegen des Indexes
zu RECHTECKE
72.9s
11.0s
(Anzahl Elemente)
25000
1. spatial join
(index overlap)
18.6s
33.0s
-299s
72652
2. spatial join
(overlap)
352.2s
159.3s
-513.7s
38802
self-join
NENNDORF
13.2s
33.1s
48029
self-join
RECHTECKE
24.1
277s
121000
Die ersten beiden Zeilen geben die Zeiten wieder, die benötigt wurden, um die Indexstrukturen zu erstellen und (bei OraGiST) diese in die Datenbank zu verschieben.
Beim ersten spatial join wird eine Anfrage an den Index über folgende Selektionen
berechnet:
select count(*) from
TABLE(join3(’overlap’, ’RECHTECKE(GEOMETRY)’,’NENNDORF(GEOMETRY)’));
bzw. mit der Oracle Spatial -Funktion sdo_filter:
select count(*) from NENNDORF N, RECHTECKE R,
where sdo_filter(r.geometry, n.geometry, ’querytype=join’)=’TRUE’;
Dabei stellte sich heraus, dass sdo_filter auf ein Vertauschen der Reihenfolge der zu
verbindenden Tabellen mit starken Performance-Verlusten reagiert. Die Verbundberechnung dauert bei einer Anfrage mit sdo_filter(n.geometry, r.geometry,. . . ) nicht
mehr etwa 33 Sekunden, sondern 299 Sekunden. Der symmetrisch arbeitende Verbundalgorithmus, der in JoinGiST verwendet wird, zeigt diese Anfälligkeit nicht.
Beim zweiten spatial join soll zusätzlich die tatsächliche Geometrie überprüft werden.
Dies geschieht mit der Methode sdo_geom.relate:
select count(*) from NENNDORF n, RECHTECKE r,
TABLE(join3(’overlap’,’NENNDORF(GEOMETRY)’,
’RECHTECKE(GEOMETRY)’)) j
where sdo_geom.relate(r.geometry, ’ANYINTERACT’, n.geometry,0.5)=’TRUE’
and r.rowid=right and n.rowid=left;
KAPITEL 8. ANWENDUNG UND PERFORMANCE
75
Oracle Spatial stellt eine Funktion zur Verfügung, die die zweite Filterstufe gleich mit
implementiert. Diese ist hier vermutlich auf Grund der besseren Anbindung an die Datenbank im Vorteil:
select count(*) from RECHTECKE r, NENNDORF n
where sdo_relate(r.geometry, n.geometry,
’mask=ANYINTERACT querytype=JOIN’)=’TRUE’;
Ändert man hier die Reihenfolge der Tabellen in sdo_relate, so ergibt sich wieder eine
deutlich schlechtere Zeit zur Berechnung des Verbundes.
Zu letzt wurde noch jeweils ein self-join über den Index berechnet (wie beim 1. spatial
join, mit dem Unterschied, dass jeweils das gleiche Objekt als Verbundpartner angegeben
wurde).
8.3
Performance-Analyse
Da der eigentliche Verbund mit JoinGiST bereits nach wenigen Sekunden berechnet
ist, und damit auch eine Anfrage ohne weitere Verknüpfungen, lohnt es sich vermutlich
nicht, hier weitere Optimierungen des Algorithmus vorzunehmen Dabei ist die VerbundBerechnung durchwegs schneller als mit den R-Bäumen des Oracle Spatial Cartridge,
obwohl die externe Implementierung vermutlich mit einem größeren Overhead beim Funktionsaufruf und einer schlechteren Anbindung an die Daten (bei Speicherung in der Datenbank) besitzt.
Soll aber nicht nur eine Verbundberechnung aufgrund der Indexdaten stattfindet, also
ohne das die tatsächlichen Objektgeometrien herangezogen werden, sondern auch ein weitere Verknüpfung mit den ursprünglichen Tabellen stattfinden, um weitere Operationen
auf den original Datensätzen ausführen zu können, so bricht die Verarbeitungsgeschwindigkeit zunehmend ein. Sie bleibt aber auf einem gleichmäßigen Niveau, im Gegensatz
zu den indexgestützten Operatoren des Spatial Cartride, die vermutlich den Index aber
einer gewissen Verbundkomplexität nicht mehr richtig verwenden könnem.
Die größte Schwachstelle bei JoinGiST ist vermutlich das Auffinden der zugehörigen
Datensätze durch die Datenbank. Diese kann nicht auf eine Zugehörigkeit der PipelineFunktion zu den anderen Tabellen schließen, so dass die üblichen Algorithmen zur Berechnung eines Verbundes zweier verschiedener Tabellen angewandt werden.
8.4
Ausblick und Verbesserungsmöglichkeiten
Es wäre möglich und erstrebenswert, eine engere Verzahnung mit OraGiST zu erreichen.
Würden die Spezialisierungen dort ebenfalls mit Erweiterungsobjekten stattfinden, statt
Unterklassen der OraGiST-Klasse zu erstellen, so könnte man diese einfach in die Erweiterungen von Join-GiST einsetzten. In diesen müsste dann praktisch nur noch die
meta_intersect-Methode und die Selektionserstellung implementiert werden. Indexnamen und Schlüssellängen könnten direkt von den OraGiST-Erweiterungen übernommen
werden.
KAPITEL 8. ANWENDUNG UND PERFORMANCE
76
Die Verbindung der Datenbank mit externen Funktionen ist nicht so effizient und flexibel, wie man es sich wünschen würde. So wäre es wünschenswert, das Indexing Interface
so zu erweitern, dass auch auch Verbundindexe möglich sind. Gut wäre auch die Möglichkeit, Indexe zu erstellen, die mehrere Attribute einer Tabelle in einer gemeinsamen
Datenstruktur halten kann, so dass gemeinsam zu indexierende Attribute nicht erst zu einem Objekttyp zusammengefasst werden müssen, um darauf eine Indexstruktur erstellen
zu können.
Anhang A
Beispiel einer OraGiST-Erweiterung
Möchte man einen benutzerdefinierten Index mit OraGiST erstellen, so sollte man zunächst den Datentyp und zugehörige Operatoren in Oracle erstellen. Zur Erstellung eines
OraGiST-Spezialisierung, verwendet man das Shell-Skript oragist. Ruft man es mit
oragist define
auf, so wird nach Angabe des Schemas und Oracle-Datentyps der indexierte werden soll,
einem Namen für die neue Spezialisierung sowie eines Oracle-Accounts mit Passwort
der Oracle Type Translator aufgerufen, um eine C-Header-Datei für diesen Datentyp
anzulegen. Zusätzlich erhält man drei weitere Dateien: Eine C++ -Header-Datei definiert
eine neue Unterklasse von OraGIST, die zu spezialisierenden Methoden brauchen nur
noch in der .cc-Datei implementiert werden. Ein SQL-Skript muss schließlich noch um
die Operatoren und den Indextyp ergänzt werden, die von der Erweiterung unterstützt
werden sollen. Der Implementationstyp des Oracle Index Implementation Types ist bereits
vorgegeben.
Sind die fehlenden Angaben in diesen Dateien implementiert, so kann mit
oragist register
OraGiST um den neuen Indextyp erweitert werden. Dabei wird odci2oragist.cc um
den neuen Indextyp erweitert, die Bibliothek wird neu kompiliert und der Indextyp in der
Datenbank eingerichtet (d.h. das SQL-Skript ausgeführt). Die Implementierungsdateien
befinden sich nun im Unterverzeichnissen des Verzeichnisses ogext, Änderungen müssen also dort vorgenommen werden. Sollte das Kompilieren fehlgeschlagen sein, so sollte
oragist register kein zweites Mal aufgerufen werden (denn dies würde zu mehrfachen
Eintragungen in odci2oragist.cc führen), sondern lediglich make ausgeführt werden.
Es folgt das Beispiel aus [Lö01] zur Indexierung des Oracle-Typs MDSYS.SDO_GEOMETRY
in der Erweiterung sdoggist (teilweise verändert, insbesondere ohne nearest neighbour Operationen, da diese nicht von JoinGiST unterstützt werden.):
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
Implementierung der typspezifischen OraGiST -Methoden:
sdoggist.cc
#include
#include
#include
#include
#include
”sdoggist.h”
”gist.h”
”gist rtpred rect.h” // FOR PREDICATES
”gist rtree.h” // FOR R−TREE EXTENSION
<stdio.h>
gist ext t ∗sdoggist :: getExt()
{
return &rt rect ext; // R−TREE EXTENSION
}
int sdoggist :: getMaxKeySize()
{
return 4 ∗ sizeof(double);
}
char ∗sdoggist::getIdxFileName(char ∗idxname)
{
char ∗tmp = new char[100];
sprintf (tmp, ”/opt/oracle/oragist−indices/%s”, idxname);
return tmp;
}
void sdoggist :: printKey(void ∗key, smsize t keysize)
{
double ∗rect = (double ∗)key;
fprintf (stderr , ”[%f, %f, %f, %f] (%d)\n”,
rect [0], rect [1], rect [2], rect [3], keysize );
}
void ∗sdoggist::approximate(DBConnectionHandle dbh,
void ∗value, void ∗value ind,
smsize t &size)
{
og MDSYS SDO GEOMETRY ∗geom
= (og MDSYS SDO GEOMETRY ∗)value;
og MDSYS SDO GEOMETRY ind ∗geom ind
= (og MDSYS SDO GEOMETRY ind ∗)value ind;
double ∗rect = new double[4];
78
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
double x, y;
int isPoint ;
if (OCINumberToInt(dbh−>errhp,
&(geom−>SDO GTYPE),
sizeof(isPoint ),
OCI NUMBER SIGNED,
(dvoid ∗)&isPoint)
!= OCI SUCCESS) return NULL;
if ( isPoint%10 == 1) // POINT TYPE
{
if (OCINumberToReal(dbh−>errhp,
&(geom−>SDO POINT.X),
sizeof(x),
(dvoid ∗)&x)
!= OCI SUCCESS) return NULL;
if (OCINumberToReal(dbh−>errhp,
&(geom−>SDO POINT.Y),
sizeof(y),
(dvoid ∗)&y)
!= OCI SUCCESS) return NULL;
rect [0] = x ; rect [1] = x;
rect [2] = y ; rect [3] = y;
}
else
// COMPLEX OBJECT
{
OCIIter
∗ iterator ;
boolean
eoc;
dvoid
∗elem;
OCIInd
∗elemind;
if (OCIIterCreate(dbh−>envhp,
dbh−>errhp,
geom−>SDO ORDINATES,
&iterator)
!= OCI SUCCESS) return NULL;
// GET FIRST X COORDINATE
if (OCIIterNext(dbh−>envhp,
dbh−>errhp,
iterator ,
&elem,
(dvoid ∗∗)&elemind,
&eoc)
!= OCI SUCCESS) return NULL;
79
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
if (OCINumberToReal(dbh−>errhp,
(OCINumber ∗)elem,
sizeof(x),
(dvoid ∗)&x)
!= OCI SUCCESS) return NULL;
// GET FIRST Y COORDINATE
if (OCIIterNext(dbh−>envhp,
dbh−>errhp,
iterator ,
&elem,
(dvoid ∗∗)&elemind,
&eoc)
!= OCI SUCCESS) return NULL;
if (OCINumberToReal(dbh−>errhp,
(OCINumber ∗)elem,
sizeof(y),
(dvoid ∗)&y)
!= OCI SUCCESS) return NULL;
rect [0] = x ; rect [1] = x;
rect [2] = y ; rect [3] = y;
sword status = OCIIterNext(dbh−>envhp,
dbh−>errhp,
iterator ,
&elem,
(dvoid ∗∗)&elemind,
&eoc);
while (!eoc && (status == OCI SUCCESS))
{
// GET REMAINING COORDINATES
if (OCINumberToReal(dbh−>errhp,
(OCINumber ∗)elem,
sizeof(x),
(dvoid ∗)&x)
!= OCI SUCCESS) return NULL;
if (OCIIterNext(dbh−>envhp,
dbh−>errhp,
iterator ,
&elem,
(dvoid ∗∗)&elemind,
&eoc)
!= OCI SUCCESS)
return NULL; // Y COORDINATE MISSING
80
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
if (OCINumberToReal(dbh−>errhp,
(OCINumber ∗)elem,
sizeof(y),
(dvoid ∗)&y)
!= OCI SUCCESS) return NULL;
if (x<rect [0]) rect [0] = x ; // SET UP
if (x>rect [1]) rect [1] = x ; // BOUNDING BOX
if (y<rect [2]) rect [2] = y ; //
if (y>rect [3]) rect [3] = y ; //
status = OCIIterNext(dbh−>envhp,
dbh−>errhp,
iterator ,
&elem,
(dvoid ∗∗)&elemind,
&eoc);
}
OCIIterDelete(dbh−>envhp, dbh−>errhp, &iterator);
}
size = 4 ∗ sizeof(double);
return rect;
}
gist query t ∗sdoggist :: getQuery(DBConnectionHandle dbh)
{
rt rect ∗r1
= new rt rect(2, (double ∗)qi−>appr cmpval);
int pred;
pred = ((qi−>start && ∗(qi−>start))
? rt query t :: rt overlap
: rt query t :: rt nooper);
return new rt query t((rt query t::rt oper)pred,
rt query t :: rt rectarg ,
(rt pred ∗)r1 );
}
bool sdoggist::needVerify()
{
: true;
// ... WHEREAS ”sdorel” NEEDS VERIFY
}
81
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
gist query t ∗sdoggist :: getEqualsQuery(DBConnectionHandle dbh,
void ∗value,
void ∗value ind)
{
smsize t size ;
rt rect ∗r1
= new rt rect(2, (double ∗)approximate(dbh,
value , value ind,
size ));
return new rt query t
((rt query t :: rt oper)rt query t :: rt equal ,
rt query t :: rt rectarg ,
(rt pred ∗)r1 );
}
82
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
Headerdatei der Klasse sdoggist:
sdoggist.h
#ifndef sdoggist ULO
# define sdoggist ULO
#include <oragist.h>
#include <oci.h>
#include <sdoggist oratype.h>
class sdoggist :public OraGiST
{
public:
sdoggist(DBConnectionHandle dbh = NULL)
: OraGiST(dbh) {}
// BASE−CLASS CONSTRUCTOR
gist ext t ∗getExt();
int getMaxKeySize();
char ∗getIdxFileName(char ∗idxname);
void printKey(void ∗key, smsize t keysize);
void ∗approximate(DBConnectionHandle dbh,
void ∗value,
void ∗value ind,
smsize t &size );
gist query t ∗getQuery(DBConnectionHandle dbh);
bool needVerify();
gist query t ∗getEqualsQuery(DBConnectionHandle dbh,
void ∗value,
void ∗value ind);
};
#endif
83
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
Headerdatei für den Datentyp (Pendant zu MDSYS.SDO_GEOMETRY):
sdoggist_oratype.h
#ifndef SDOGGIST ORATYPE ORACLE
# define SDOGGIST ORATYPE ORACLE
#ifndef OCI ORACLE
# include <oci.h>
#endif
typedef
typedef
typedef
typedef
OCIRef og MDSYS SDO GEOMETRY ref;
OCIRef SDO POINT TYPE ref;
OCIArray SDO ELEM INFO ARRAY;
OCIArray SDO ORDINATE ARRAY;
struct SDO POINT TYPE
{
OCINumber X;
OCINumber Y;
OCINumber Z;
};
typedef struct SDO POINT TYPE SDO POINT TYPE;
struct SDO POINT TYPE ind
{
OCIInd atomic;
OCIInd X;
OCIInd Y;
OCIInd Z;
};
typedef struct SDO POINT TYPE ind SDO POINT TYPE ind;
struct og MDSYS SDO GEOMETRY
{
OCINumber SDO GTYPE;
OCINumber SDO SRID;
struct SDO POINT TYPE SDO POINT;
SDO ELEM INFO ARRAY ∗ SDO ELEM INFO;
SDO ORDINATE ARRAY ∗ SDO ORDINATES;
};
typedef struct og MDSYS SDO GEOMETRY
og MDSYS SDO GEOMETRY;
struct og MDSYS SDO GEOMETRY ind
84
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
{
OCIInd atomic;
OCIInd SDO GTYPE;
OCIInd SDO SRID;
struct SDO POINT TYPE ind SDO POINT;
OCIInd SDO ELEM INFO;
OCIInd SDO ORDINATES;
};
typedef struct og MDSYS SDO GEOMETRY ind
og MDSYS SDO GEOMETRY ind;
#endif
85
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
Erzeugung des Indextyps in SQL:
sdoggist.sql
−− GiST extension name
−− sdoggist
−− SQL Type of indexed column :
−− MDSYS.SDO GEOMETRY
−− CREATE INDEXTYPE IMPLEMENTATION TYPE −−
create or replace type gist MDSYS SDO GEOMETRY im
as object
(
scanctx RAW(4),
static function
ODCIGetInterfaces(ifclist OUT SYS.ODCIObjectList)
return NUMBER,
static function
ODCIIndexCreate(ia SYS.ODCIIndexInfo,
parms VARCHAR2)
return NUMBER,
static function
ODCIIndexAlter(ia SYS.ODCIIndexInfo,
parms VARCHAR2,
alter option NUMBER)
return NUMBER,
static function
ODCIIndexDrop(ia SYS.ODCIIndexInfo)
return NUMBER,
static function
ODCIIndexInsert(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
newval MDSYS.SDO GEOMETRY)
return NUMBER,
static function
ODCIIndexDelete(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
oldval MDSYS.SDO GEOMETRY)
return NUMBER,
static function
ODCIIndexUpdate(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
oldval MDSYS.SDO GEOMETRY,
newval MDSYS.SDO GEOMETRY)
86
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
return NUMBER,
static function
ODCIIndexStart(sctx IN OUT
gist MDSYS SDO GEOMETRY im,
ia SYS.ODCIIndexInfo,
op SYS.ODCIPredInfo,
qi SYS.ODCIQueryInfo,
strt NUMBER,
stop NUMBER,
cmpval MDSYS.SDO GEOMETRY)
return NUMBER,
member function
ODCIIndexFetch(nrows NUMBER,
rids OUT SYS.ODCIRidList)
return NUMBER,
member function
ODCIIndexClose return NUMBER
);
/
−− CREATE IMPLEMENTATION UNIT −−
create or replace type body gist MDSYS SDO GEOMETRY im
is
static function
ODCIGetInterfaces(ifclist OUT SYS.ODCIObjectList)
return NUMBER is
begin
ifclist
:= SYS.ODCIObjectList
(sys .ODCIObject(’SYS’,’ODCIINDEX1’));
return ODCIConst.Success;
end ODCIGetInterfaces;
static function
ODCIIndexCreate(ia SYS.ODCIIndexInfo,
parms VARCHAR2)
return NUMBER
as external
name ”ODCIIndexCreate C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
87
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
parms,
return OCINUMBER);
static function
ODCIIndexAlter(ia SYS.ODCIIndexInfo,
parms VARCHAR2,
alter option NUMBER)
return NUMBER
as external
name ”ODCIIndexAlter C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
alter option ,
alter option indicator ,
parms,
return OCINUMBER);
static function
ODCIIndexDrop(ia SYS.ODCIIndexInfo)
return NUMBER
as external
name ”ODCIIndexDrop C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
return OCINUMBER);
static function
ODCIIndexInsert(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
newval MDSYS.SDO GEOMETRY)
return NUMBER
as external
name ”ODCIIndexInsert C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
rid , rid indicator ,
88
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
newval, newval indicator struct ,
return OCINUMBER);
static function
ODCIIndexDelete(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
oldval MDSYS.SDO GEOMETRY)
return NUMBER
as external
name ”ODCIIndexDelete C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
rid , rid indicator ,
oldval , oldval indicator struct ,
return OCINUMBER);
static function
ODCIIndexUpdate(ia SYS.ODCIIndexInfo,
rid VARCHAR2,
oldval MDSYS.SDO GEOMETRY,
newval MDSYS.SDO GEOMETRY)
return NUMBER
as external
name ”ODCIIndexUpdate C”
library oragist
with context parameters (
context,
ia , ia indicator struct ,
rid , rid indicator ,
oldval , oldval indicator struct ,
newval, newval indicator struct ,
return OCINUMBER);
static function
ODCIIndexStart(sctx IN OUT
gist MDSYS SDO GEOMETRY im,
ia SYS.ODCIIndexInfo,
op SYS.ODCIPredInfo,
qi SYS.ODCIQueryInfo,
strt NUMBER,
stop NUMBER,
89
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
cmpval MDSYS.SDO GEOMETRY)
return NUMBER
as external
name ”ODCIIndexStart C”
library oragist
with context parameters (
context,
sctx , sctx indicator struct ,
ia , ia indicator struct ,
op, op indicator struct ,
qi , qi indicator struct ,
strt , strt indicator ,
stop , stop indicator ,
cmpval, cmpval indicator struct ,
return OCINUMBER);
member function
ODCIIndexFetch(nrows NUMBER,
rids OUT SYS.ODCIRidList)
return NUMBER
as external
name ”ODCIIndexFetch C”
library oragist
with context parameters (
context,
self , self indicator struct ,
nrows, nrows indicator,
rids , rids indicator ,
return OCINUMBER);
member function
ODCIIndexClose return NUMBER
as external
name ”ODCIIndexClose C”
library oragist
with context parameters (
context,
self , self indicator struct ,
return OCINUMBER);
end;
/
−−−−−−−−− CREATE OPERATOR RELATE −−−−−−−−−
90
ANHANG A. BEISPIEL EINER ORAGIST-ERWEITERUNG
create function mysdorelate(m1 MDSYS.SDO GEOMETRY,
m2 MDSYS.SDO GEOMETRY)
return number is
val number;
begin
if sdo geom.relate(
m1,
MDSYS.SDO DIM ARRAY(
MDSYS.SDO DIM ELEMENT(’X’, 354100000,
355700000, 1),
MDSYS.SDO DIM ELEMENT(’Y’, 579800000,
581200000, 1)),
’ANYINTERACT’, m2,
MDSYS.SDO DIM ARRAY(
MDSYS.SDO DIM ELEMENT(’X’, 354100000,
355700000, 1),
MDSYS.SDO DIM ELEMENT(’Y’, 579800000,
581200000, 1)))
= ’TRUE’
then val := 1;
else val := 0;
end if ;
return val ;
end;
/
create operator sdorel binding (MDSYS.SDO GEOMETRY,
MDSYS.SDO GEOMETRY)
return number
using mysdorelate;
−−− CREATE INDEXTYPE FOR SDOREL −−−
create indextype sdoggist 01 for
sdorel(MDSYS.SDO GEOMETRY, MDSYS.SDO GEOMETRY),
using gist MDSYS SDO GEOMETRY im;
91
Anhang B
Beispiel einer JoinGiST-Erweiterung
Um eine neue JoinGiST-Erweiterung zu implementieren, wird ebenfalls ein kleines ShellSkript verwendet, um den Anwender bei dieser Aufgabe zu unterstützen.
Existiert noch kein Objekt für den Rückgabewert, so wird dieses mit
joingist init
in der Datenbank angelegt. Dabei wird das SQL-Skript joingist_resultimpl.sql ausgeführt, das zusätzlich gleich den Implementierungs-Typ des ODCITable Interfaces anlegt. Um diese Skript ausführen zu können, ist die Angabe von Username und Passwort
notwendig. Da diese als Parameter zu sqlplus auf der Eingabezeile erscheinen, wird sicherheitsbewussten Anwendern empfohlen den Typ direkt aus sqlplus erstellen (es wird
die Berechtigung Objekte in Oracle erstellen zu dürfen benötigt):
@’/pfad/zu/joingist_resultimpl.sql’
Damit die Implementierung die Bibliothek mit dem Alias joingist findet, muss zusätzlich
mit
create library joingist as ’/pfad/zu/joingist.so’
in sqlplus der Pfadname der Bibliothek bekannt gemacht werden. (Dazu benötigt man
Rechte, um in Oracle Bibliotheken erstellen zu dürfen)
Um eine neue Unterklasse der JoinGiST-Erweiterungsklasse JoinGiST_ext_t zu erstellen, ruft verwendet man:
joingist create
Es werden die Namen der beiden OraGiST-Erweiterungsklassen abgefragt, für die der Verbund implementiert werden soll. Daraus ergibt sich der Basisname der neuen JoinGiSTErweiterungsklasse und es werden zwei Dateien dazu erstellt: Eine Header-Datei, die
diese Klasse als Unterklasse von JoinGiST_ext_t deklariert und ein Datei, in der die
C++ -Methoden implementiert werden müssen. Zusätzlich wird die Datei odci2join.cc
um eine Abfrage für diese Spezialisierungs-Kombination erweitert, so dass das neue Objekt bei einem Verbundaufruf der Klasse JoinGiST übergeben werden kann.
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
Definition des Rückgabeobjektes und der ODCITable-Implementation:
joingist_resultimpl.sql
CREATE TYPE join result type AS OBJECT (
left VARCHAR2(18),
right VARCHAR2(18)
);
CREATE TYPE join result set IS TABLE OF join result type;
CREATE OR REPLACE TYPE join result impl AS OBJECT (
key RAW(4),
STATIC FUNCTION ODCITableStart(sctx OUT join result impl,
op IN STRING, t1 IN STRING, t2 IN STRING,
s1 IN STRING, s2 IN STRING, add IN STRING)
RETURN BINARY INTEGER
AS LANGUAGE C
LIBRARY joingist
NAME ”ODCITableStart 6”
WITH CONTEXT
PARAMETERS (
context,
sctx , sctx INDICATOR STRUCT,
op, t1 , t2 , s1 , s2 , a,
RETURN),
STATIC FUNCTION ODCITableStart(sctx OUT join result impl,
op IN STRING, t1 IN STRING, t2 IN STRING,
s1 IN STRING, s2 IN STRING)
RETURN BINARY INTEGER
AS LANGUAGE C
LIBRARY joingist
NAME ”ODCITableStart 5”
WITH CONTEXT
PARAMETERS (
context,
sctx , sctx INDICATOR STRUCT,
op, t1 , t2 , s1 , s2,
RETURN),
STATIC FUNCTION ODCITableStart(sctx OUT join result impl,
op1 IN STRING, t1 IN STRING, t2 IN STRING)
RETURN BINARY INTEGER
AS LANGUAGE C
93
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
LIBRARY joingist
NAME ”ODCITableStart 3”
WITH CONTEXT
PARAMETERS (
context,
sctx , sctx INDICATOR STRUCT,
op1, t1 , t2,
RETURN),
MEMBER FUNCTION ODCITableFetch(self IN OUT join result impl,
nrows IN NUMBER,
rslt OUT join result set)
RETURN BINARY INTEGER
AS LANGUAGE C
LIBRARY joingist
NAME ”ODCITableFetch”
WITH CONTEXT
PARAMETERS (
context,
self , self INDICATOR STRUCT,
nrows,
rslt , rslt INDICATOR,
RETURN),
MEMBER FUNCTION ODCITableClose(self IN join result impl)
RETURN BINARY INTEGER
AS LANGUAGE C
LIBRARY joingist
NAME ”ODCITableClose”
WITH CONTEXT
PARAMETERS (
context,
self , self INDICATOR STRUCT,
RETURN)
);
/
CREATE FUNCTION join3(op IN STRING, t1 IN STRING, t3 IN STRING)
RETURN JOIN RESULT SET
PIPELINED USING join result impl;
/
CREATE FUNCTION join5(op IN STRING, t1 IN STRING, t3 IN STRING,
s1 IN STRING, s2 IN STRING)
RETURN JOIN RESULT SET
94
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
PIPELINED USING join result impl;
/
CREATE FUNCTION join6(op IN STRING, t1 IN STRING, t3 IN STRING,
s1 IN STRING, s2 IN STRING, a IN STRING)
RETURN JOIN RESULT SET
PIPELINED USING join result impl;
/
95
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
Headerdatei der Erweiterungs-Klasse sdoggist_sdoggist:
join_sdoggist_sdoggist.h
#include ”gist rtpred rect.h” //for query predicates
#include ”joingist.h”
class sdoggist sdoggist : public JoinGiST ext t{
public:
bool setOperator(string ∗&op);
gist query t ∗getLeftQuery(string ∗&selection);
gist query t ∗getRightQuery(string ∗&selection);
char ∗getLeftIdxFileName(char ∗idxname);
char ∗getRightIdxFileName(char ∗idxname);
int getLeftMaxKeySize();
int getRightMaxKeySize();
bool meta intersect(const void ∗key1, const bool &leaf1,
const void ∗key2, const bool &leaf2);
protected:
bool equalOp;
};
96
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
Implementierung der typspezifischen JoinGiST -Methoden:
join_sdoggist_sdoggist.cc
#include ”join sdoggist sdoggist.h”
//join with two indexes of type sdoggist
#include <string>
bool sdoggist sdoggist :: setOperator(string ∗&op){
// if keyword equal is present : equality−join
if (op==NULL) return false; //no real string
if (op−>find(”equal”)==op−>npos){
//not found
equalOp=false;
} else {
//find () returned something smaller than npos:
//”equal”−>found
equalOp=true;
}
return true;
}
gist query t ∗ sdoggist sdoggist :: getLeftQuery(string ∗&selection){
//parse a string of the form ”x1, y1, x2, y2”
if (! selection ) return NULL; //selection−pointer is NULL
double ∗rect coordinates=new double[4];
string :: size type index1=0;
//rect coordinate order is
//x low, x high,y low ,y high
rect coordinates[0]=atof( selection −>c str());
// x low set
index1=selection−>find(’,’, index1+1);
if (index1 != selection −>npos){
rect coordinates[2]=atof(( selection −>c str()+index1+1));
} else {
return NULL; //something went wrong
} // y low set
index1=selection−>find(’,’, index1+1);
if (index1 != selection −>npos){
rect coordinates[1]=atof(( selection −>c str()+index1+1));
} else {
97
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
return NULL; //something went wrong
} // x high set
index1=selection−>find(’,’, index1+1);
if (index1 != selection −>npos){
rect coordinates[3]=atof(( selection −>c str()+index1+1));
} else {
return NULL; //something went wrong
} // y high set
rt rect ∗rect=new rt rect(2,rect coordinates);
gist query t ∗query=new rt query t(rt query t::rt overlap,
rt query t :: rt rectarg , rect );
return query;
}
gist query t ∗ sdoggist sdoggist :: getRightQuery(string ∗&selection){
//same as left query ...
return getLeftQuery(selection);
}
//this is from sdoggist.cc : ”getIdxFileName()”
char ∗sdoggist sdoggist :: getLeftIdxFileName(char ∗idxname){
char ∗tmp = new char[100];
sprintf (tmp, ”/opt/oracle/oragist−indices/%s”, idxname);
return tmp;
}
//it might be, that you store your different Indexes in different directories
char ∗sdoggist sdoggist :: getRightIdxFileName(char ∗idxname){
char ∗tmp = new char[100];
sprintf (tmp, ”/opt/oracle/oragist−indices/%s”, idxname);
return tmp;
}
//this is from sdoggist.cc : ”getLeftKeySize()”
int sdoggist sdoggist :: getLeftMaxKeySize()
{
return 4 ∗ sizeof(double);
}
int sdoggist sdoggist :: getRightMaxKeySize()
{
98
ANHANG B. BEISPIEL EINER JOINGIST-ERWEITERUNG
return 4 ∗ sizeof(double);
}
bool sdoggist sdoggist :: meta intersect(const void ∗key1, const bool &leaf1,
const void ∗key2, const bool &leaf2){
//we support two Operators: intersection and equality
//for equality equalOp will be set , otherwise test for intersection
double ∗rect1=(double ∗)key1;
double ∗rect2=(double ∗)key2;
//equality : leaf entrys must be equal,
//
other nodes just have to overlap
if ( leaf1 && leaf2)
if (equalOp==true)
if (( rect1[0]==rect2[0]) &&
(rect1[1]==rect2[1]) &&
(rect1[2]==rect2[2]) &&
(rect1[3]==rect2[3]))
return (true);
else return (false);
//test for intersection : return false if they do not overlap
//(here we count ”touching” towards ”overlapping”)
// if a.high < b.low
or
a.low > b.high −−> no overlap
if (( rect1 [1] < rect2 [0]) || ( rect1 [0] > rect2 [1]))
return (false);
if (( rect1 [3] < rect2 [2]) || ( rect1 [2] > rect2 [3]))
return (false);
return (true);
}
99
Literaturverzeichnis
[Aok98]
Paul M. Aoki: Generalizing Search in Generalized Search Trees Proceedings
of the 14th International Conference on Data Engineering, Orlando, Februar
1998, S. 380-389
[AK01]
Paul M. Aoki, Marcel Kornacker: Guide to Writing Extensions
http://gist.cs.berkeley.edu/libgist-2.0/ext_guide.html, März 2001
[BKS93]
Thomas Brinkhoff, Hans-Peter Kriegel, Bernhard Seeger: Efficient Processing
of Spatial Joins Using R-trees Proceedings of ACM SIGMOD International
Conference on Management of Data, Mai 1993, S. 237-246
[BKSS90] Norbert Beckmann, Hans-Peter Kriegel, Ralf Schneider, Bernhard Seeger: The
R∗ -tree: An Efficient and Robust Access Method For Points and Rectangles
Proceedings of the ACM SIGMOD International Conference on Management
of Data, Atlantic City, Mai 1990, S. 322-331.
[Com79]
Douglas Comer: The Ubiquitous B-Tree Computing Surveys, 11(2): S. 121-137,
Juni 1979
[GiST-PSQL] Teodor
Sigaev,
Oleg
Bartunov:
GiST
for
PostgreSQL
http://www.sai.msu.su/~megera/postgres/gist/, Mai 2003
[GiST-PGIS] Dave Blasby (Principal Developer) et al.: PostGIS: Geographic Objects for
PostgreSQL http://postgis.refractions.net/
[GPL]
GNU General Public License
[Gut84]
A. Guttman: R-trees: A Dynamic Index Structure for Spatial Searching Proceedings of ACM SIGMOD International Conference on Management of Data,
Boston, 1984, S. 47-57
http://www.gnu.org/copyleft/gpl.html
[HLR97] Yum-Wu Huang, Ning Jing, Elke A. Rundensteiner: Spatial Joins Using Rtrees: Breadth-First Traversal with Global Optimizations Proceedings of the
23rd VLDB Conference, Athen, 1997
[HNP95] Joseph M. Hellerstein, Jeffrey F. Naughton, Avi Pfeffer: Generalized Search
Trees for Database Systems Technical Report #1274, University of Wisconsin
at Madison, July 1995
LITERATURVERZEICHNIS
101
siehe auch: Generalized Search Trees for Database Systems (Extended Abstract)
Proceedings of the 21st VLDB Conference, Zürich, Schweiz, 1995, S. 562-573
[HR01]
Theo Härder, Erhard Rahm: Datenbanksysteme: Konzepte und Techniken der
Implementierung 2. Auflage, Berlin, Heidelberg, New York, Barcelona, Hongkong, London, Mailand, Paris, Tokio, 2001, Springer-Verlag
[JS93]
Theodore Johnson, Dennis Shasha: Why Free-at-Empty Is Better Than Mergeat-Half Journal of Computer Sciences and Systems, 47(1), August 1993, S.
45-76
[Kle03]
Carsten Kleiner: Modelling Spatial, Temporal and Spatio-Temporal Data in
Object-Relational Database Systems Dissertation, Fachbereich Informatik, Universität Hannover, 2003
[KL03]
Carsten Kleiner, Udo W. Lipeck: OraGiST - How to Make User-Defined Indexing Become Usable and Useful G. Weikum, H. Schöning, E. Rahm (eds.),
BTW 2003 - Datenbanksysteme für Business, Technologie und Web - Tagungsband der 10. BTW-Konferenz 26.-28.2.2003, Leipzig, LNI P-26, GI, Bonn, 2003,
S. 324-334.
[Li97]
Udo Lipeck: Datenbanksysteme Vorlesung am Institut für Informatik, Fachgebiet Datenbanken und Informationssysteme im Wintersemester 1997/98, Universität Hannover
[Lö01]
Ulf Löckmann: Erweiterung eines objektrelationalen Datenbankmanagementsystems um verallgemeinerte Suchbäume als Indexstrukturen Diplomarbeit am
Institut für Informatik, Fachgebiet Datenbanken und Informationssysteme,
Universität Hannover, Mai 2001
[LR95]
Ming-Ling Lo, Chinya V. Ravishankar: Generating seeded trees from data sets
The Fourth International Symposium on Large Spatial Databases (Advances
in Spatial Databases: SSD ’95), Portland, Maine, August 1995, Springer-Verlag
[LR96]
Ming-Ling Lo, Chinya V. Ravishankar: Spatial Hash-Joins Proceedings of
ACM SIGMOD International Conference on Management of Data, Montreal, Juni 1996, S. 247-258
[LR94]
Ming-Ling Lo, Chinya V. Ravishankar: Spatial Joins Using Seeded Trees Proceedings of ACM SIGMOD International Conference on Management of Data,
Minneapolis, Mai 1994, S. 209-220
[LR98]
Ming-Ling Lo, Chinya V. Ravishankar: The Desing and Implementation of
Seeded Trees: An Efficient Method for Spatial Joins IEEE Transactions on
Knowledgment and Data Engineering, Vol. 10, Nr. 1, Januar/Februar 1998, S.
136-152
LITERATURVERZEICHNIS
102
[OM84]
Jack A. Orenstein, T. H. Merrett: A Class of Data Structures for Associative
Searching Proceedings of the 4th ACM SIGACT-SIGMOD-SIGARTS Symposium on Principles of Database Systems, ACM Press, New York, 1984, S.
181-190
[OM88]
Jack A. Orenstein, Frank A. Manola: PROBE Spatial Data Modeling and Query Processing in an Image Database Application IEEE Transactions on Software Engineering, Vol. 14, Nr. 5 Mai 1988, S. 611-629
[O9i-CIPG] Jack Melnick: Oracle9i Call Interface Programmer’s Guide (Release 2)
Oracle Corporation, März 2002
[O9i-DCDG] William Gietz: Oracle9i Data Cartridge Developer’s Guide (Release 2)
Oracle Corporation, März 2002
[O9i-DPTG] Connie Dialeris Green: Oracle9i Database Performance Tuning Guide and
Reference (Release 2) Oracle Corporation, Oktober 2002
[O9i-DWG] Paul Lane: Oracle9i Data Warehousing Guide (Release 2) Oracle Corporation, März 2002
[O9i-PCP] Syed Mujeeb Ahmed, Jack Melnick, Neelam Singh, Tim Smith: Pro*C/C++
Precompiler Programmer’s Guide (Release 2) Oracle Corporation, März 2002
[O9i-SUG] Chuck Murray: Oracle9i Spatial User’s Guide and Reference Oracle Corporation, Juni 2001
[Pea90]
G. Peano: Sur une courbe qui remplit toute une aire plane Mathematische
Annalen 36, 1890, S. 157-160
Erklärung
Hiermit versichere ich, dass ich die vorliegende Arbeit und die zugehörige Implementierung selbstständig verfasst und dabei nur die angegebenen Quellen und Hilfsmittel
verwendet habe.
Hannover, 27. Juni 2003
Oliver Schweer