Arbeit und Energie

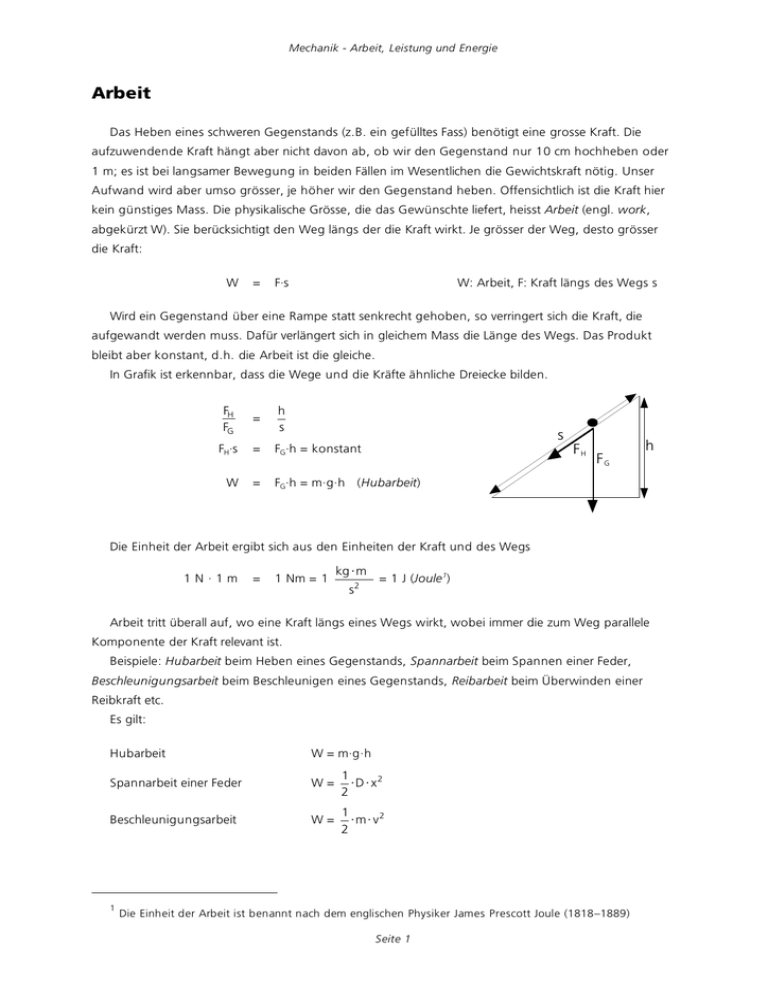
Mechanik - Arbeit, Leistung und Energie
Arbeit
Das Heben eines schweren Gegenstands (z.B. ein gefülltes Fass) benötigt eine grosse Kraft. Die
aufzuwendende Kraft hängt aber nicht davon ab, ob wir den Gegenstand nur 10 cm hochheben oder
1 m; es ist bei langsamer Bewegung in beiden Fällen im Wesentlichen die Gewichtskraft nötig. Unser
Aufwand wird aber umso grösser, je höher wir den Gegenstand heben. Offensichtlich ist die Kraft hier
kein günstiges Mass. Die physikalische Grösse, die das Gewünschte liefert, heisst Arbeit (engl. work,
abgekürzt W). Sie berücksichtigt den Weg längs der die Kraft wirkt. Je grösser der Weg, desto grösser
die Kraft:
W
=
F·s
W: Arbeit, F: Kraft längs des Wegs s
Wird ein Gegenstand über eine Rampe statt senkrecht gehoben, so verringert sich die Kraft, die
aufgewandt werden muss. Dafür verlängert sich in gleichem Mass die Länge des Wegs. Das Produkt
bleibt aber konstant, d.h. die Arbeit ist die gleiche.
In Grafik ist erkennbar, dass die Wege und die Kräfte ähnliche Dreiecke bilden.
!
FH
FG
=
h
s
FH·s
=
FG·h = konstant
!
W
=
FG·h = m·g·h (Hubarbeit)
s
FH
FG
h
Die Einheit der Arbeit ergibt sich aus den Einheiten der Kraft und des Wegs
1N·1m
=
1 Nm = 1
kg " m
s2
= 1 J (Joule 1)
Arbeit tritt überall auf, wo eine Kraft längs eines Wegs wirkt, wobei immer die zum Weg parallele
Komponente der Kraft relevant ist.!
Beispiele: Hubarbeit beim Heben eines Gegenstands, Spannarbeit beim Spannen einer Feder,
Beschleunigungsarbeit beim Beschleunigen eines Gegenstands, Reibarbeit beim Überwinden einer
Reibkraft etc.
Es gilt:
Hubarbeit
W = m·g·h
Spannarbeit einer Feder
W=
1
" D " x2
2
Beschleunigungsarbeit
W=
1
" m " v2
2
!
!
1
Die Einheit der Arbeit ist benannt nach dem englischen Physiker James Prescott Joule (1818–1889)
Seite 1
Mechanik - Arbeit, Leistung und Energie
Leistung
Bei der Arbeit spielt die Zeit, die für das Erbringen einer Arbeit nötig ist, keine Rolle. Wenn wir die
Zeit zusätzlich berücksichtigen, erhalten wir die physikalische Grösse der Leistung (engl. power,
abgekürzt P).
P
1J
1s
!
=
=
W
t
1
t: Zeit für die Arbeit W
J
= 1 W (Watt2)
s
Es gilt zu beachten, dass der Buchstabe W einerseits für die physikalische Grösse der Arbeit, aber
!
! für die Leistung
auch als Einheit
verwendet wird.
Aus der Einheit der Leistung lässt sich eine zweite Einheit für die Arbeit ableiten, die im Alltag
Verwendung findet: Die Kilowattstunde.
1’000 W · 3’600 s
=
1 kW · 1 h = 1 kWh
3.6·106 J
=
1 kWh
Energie
Die Arbeit, die beim Heben eines Gegenstands aufgewendet wird, ist in der höheren Lage des
Gegenstands gespeichert und kann wieder zurück gewonnen werden. Das Gleiche gilt für eine
gespannte Feder oder einen beschleunigten Gegenstand. Gespeicherte Arbeit wird Energie genannt.
Hubarbeit führt zu Lageenergie (potentielle Energie). Die Energie, die in einer gespannten Feder
steckt, wird ebenfalls potentielle Energie genannt. Ein sich bewegender Gegenstand hat
Bewegungsenergie (kinetische Energie).
Diese Energieformen können durch Arbeit in einander umgeformt werden. Z.B. verliert ein fallender
Gegenstand potentielle Energie und gewinnt durch Beschleunigungsarbeit kinetische Energie.
Beachten Sie den Unterschied:
Energie bezeichnet einen Zustand von gespeicherter Arbeit.
Arbeit bezeichnet einen Vorgang, bei dem eine Form der Energie in eine andere umgewandelt wird.
Potentielle und kinetische Energie werden mechanische Energieformen genannt. Daneben sind aber
viele weitere Energieformen vorhanden: Wärme (innere Energie), Elektrische Energie, Strahlungsenergie,
chemische Energie, Kernenergie.
Energieerhaltungssatz: Die Gesamtenergie eines abgeschlossenen Systems ist konstant.
Die Umwandlung von einer Energieform in eine andere ist in der Praxis nicht in allen Fällen
vollständig möglich. Wärme etwa lässt sich niemals vollständig in mechanische Energie umwandeln.
2
Die Einheit der Leistung ist benannt nach dem englischen Erfinder James Watt (1736–1819)
Seite 2