AUSWERTUNG: ELEKTRISCHE WIDERSTÄNDE Mit Hilfe einer

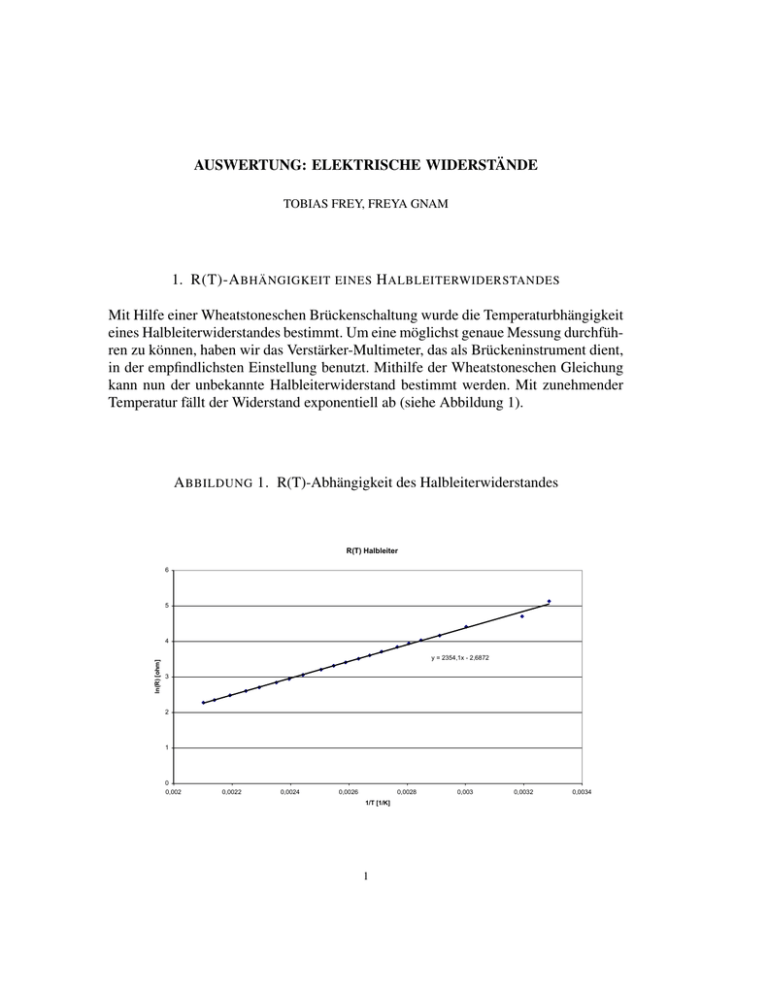
AUSWERTUNG: ELEKTRISCHE WIDERSTÄNDE
TOBIAS FREY, FREYA GNAM
1. R(T)-A BHÄNGIGKEIT EINES H ALBLEITERWIDERSTANDES
Mit Hilfe einer Wheatstoneschen Brückenschaltung wurde die Temperaturbhängigkeit
eines Halbleiterwiderstandes bestimmt. Um eine möglichst genaue Messung durchführen zu können, haben wir das Verstärker-Multimeter, das als Brückeninstrument dient,
in der empfindlichsten Einstellung benutzt. Mithilfe der Wheatstoneschen Gleichung
kann nun der unbekannte Halbleiterwiderstand bestimmt werden. Mit zunehmender
Temperatur fällt der Widerstand exponentiell ab (siehe Abbildung 1).
A BBILDUNG 1. R(T)-Abhängigkeit des Halbleiterwiderstandes
R(T) Halbleiter
6
5
ln(R) [ohm]
4
y = 2354,1x - 2,6872
3
2
1
0
0,002
0,0022
0,0024
0,0026
0,0028
1/T [1/K]
1
0,003
0,0032
0,0034
A BBILDUNG 2. Logarithmische Auftragung
R (T)
180
160
140
R [ohm]
120
100
80
60
40
20
0
0
50
100
150
200
250
T [°C]
Zur Bestimmung der temperaturabhängigen Widerstandsgleichung tragen wir den Logarithmus des Widerstandes über den Kehrwert der Temperatur auf (siehe Abbildung
2).
Aus der resultierenden Geradengleichung lassen sich die gesuchten Koeffizienten a
und b bestimmen. Es gilt: a = 68, 1 mΩ und b = 2354, 1 K
Für die Widerstandsgleichung ergibt sich somit:
R(T ) = 68 mΩ · e
2354 K
T
2. B ESTIMMUNG VERSCHIEDENER W IDERSTÄNDE
2.1. I(U)-Abhängigkeit eines Edelmetallwiderstandes (oszillographisch). Mittels
der Halbwellenschaltung des Experimentiergerätes wurde die I(U)-Abhängigkeit von
Platin bei Zimmertemperatur bestimmt (siehe Messprotokoll). Wie wir vermutet haben
besteht ein linearer Zusammenhang zwischen Spannung und Strom.
2
2.2. Vergleich von Heiß- und Kaltwiderstand einer 60 W-Birne. Wir messen einen
Kaltwiderstand der Glühbirne von 64, 13 Ω. Dies ist deutlich weniger als der notwendige Betriebswiderstand von 807 Ω. Daher fließt nach dem Einschalten kurzzeitig ein
sehr großer Strom. Durch die Erwärmung steigt der Widerstand dann rasch auf den
Betriebswiderstand an.
2.3. Kaltwiderstand einer 50 W-Kohlefadenlampe. Wie in der vorherigen Aufgabe messen wir den Kaltwiderstand der Kohlefadenlampe mit dem Ohmmeter und vergleichen diesen mit dem Betriebswiderstand der Kohlefadenlampe. Wir messen einen
Kaltwiderstand von 1690 Ω. Der Betriebswiderstand beträgt nur 968 Ω. Bei Kohlenstoff nimmt der Widerstand mit zunehmender Temperatur ab. Um auf den notwendigen Betriebswiderstand zu kommen muss die Kohlenstofflampe weniger heiß werden
als die Wolframlampe. Man erkennt, dass sie sich nach dem Einschalten langsamer
aufhellt als die Wolframlampe.
3. O SZILLOGRAPHISCHE B ESTIMMNUNG DER I(U)-A BHÄNGIGKEIT
VERSCHIEDER D IODEN UND DES VARISTORS
Die Kennlinien der Dioden und des Varistors finden sich in unserem Messprotokoll
skizziert. Sie entsprechen unseren Erwartungen. Bei der Aufzeichnung mussten wir
beachten, das der y-Eingang des Oszilloskop verpolt wurde, damit die Masse am gleichen Potential abgegriffen werden kann. Daher war im Oszillosgraphenbild der positive Strom auf der negativen y-Achse aufgezeichnet. Wir haben die Kennlinien jedoch
gespiegelt und so aufgetragen, dass sich der richtige Verlauf ergibt.
Bei der Silizium- und Germaniumdiode konnten wir kein Strom in Sperrrichtung messen. Dies liegt daran, dass die Spannung der Halbwellenschaltung bei diesem Versuchsaufbau unterhalb der Durchbruchspannung bleibt. Bei der Zener–Diode war ein
Strom in Sperrrichtung messbar, da für den Zener-Durchbruch bereits kleine Spannungen ausreichen.
Wir haben die Dioden mit einem Fön erwärmt, konnten jedoch keinen deutlichen Unterschied zum kalten Zustand beobachten.
4. W IEDERHOLUNG DER I(U)-A BHÄNGIGKEIT DES VARISTORS DURCH
PUNKTWEISE S TROM - UND S PANNUNGSMESSEUNG
Wir haben wie schon in Aufgabe 3.4 die Kennlinie eines Varistors bestimmt, diesmal
aber durch punktweise Strom- und Spannungsmessung (siehe Abbildung 3). Diese
Messkurve ist von der Form U = c · I b . Wir erhalten aus der logarithmischen Auftragung (siehe Abbildung 4) die Werte für b und c. Es gilt:
U = 3, 624 · I 0,3553
3
A BBILDUNG 3. I(U)-Abhängigkeit des Varistors
I(U) Varistor
50
40
30
20
I [mA]
10
0
-15
-10
-5
0
5
10
15
-10
-20
-30
-40
-50
U [V]
A BBILDUNG 4. Logarithmische Auftragung Varistor
I(U) Varistor -b&c Bestiimung
3
2,5
y = 0,3553x + 1,2876
2
ln(U) [V]
1,5
1
0,5
0
-5
-4
-3
-2
-1
0
-0,5
ln(I) [mA]
4
1
2
3
4
5
A BBILDUNG 5. I(U)-Abhängigkeit der Tunneldiode
I (U) Tunneldiode - punktförmig gemessen
300
200
Innenwiderstand 1700 ohm
I [müA]
100
0
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
-100
-200
Innenwiderstand 600 ohm
-300
U [V]
5. T UNNELDIODE
5.1. I(U)-Abhängigkeit der Tunneldiode durch punktweise Strom- und Spannungsmessung. Um die I(U)-Abhängigkeit der Tunneldiode zu bestimmen, haben wir die
Spannungsteilerschaltung am Experimetiergerät verwendet. Die Messung erfolgte im
300 µA- Bereich. Daher liegt der Innenwiderstand des Strommessgerätes bei Ri =
600 Ω, weshalb die Arbeitsgerade des Multizets die Kurve der Tunneldiode nur in
einem Punkt schneidet. Dadurch tritt keinSprungverhalten der Stromstärke auf. Der
Stromverlauf in Abhängigkeit der Spannung ist in Abbildung 5 aufgetragen.
Die Eigenschaften einer Tunneldiode sind gut erkennbar. Das lokale Maximum des
Tunneleffektes liegt bei I = 0, 03 µA und U = 120 mV (Höckerspannung). Hier ist
es für die Elektronen energetisch am günstigsten vom Valenzband zum Leitungsband
zu tunneln. Mit zunehmender Spannung benötigen die Elektronen weniger Energie
um die Grenzschicht zu umlaufen, als dafür, sie zu durchtunneln. Dies zeigt sich in
dem zweiten Anstieg der Stromstärke. Das lokale Minimum der Leitfähigkeit liegt bei
I = 0, 25 µA und U = 20 mV (Talspannung).
5
A BBILDUNG 6. Widerstand der Tunneldiode in Abhängigkeit von der Spannung
Tunneldiode -Widerstand
16000
14000
12000
R [ohm]
10000
8000
6000
4000
2000
0
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
U [V]
A BBILDUNG 7. Differentieller Widerstand in Abhängigkeit von der Spannung
differentieller Widerstand
100
50
0
dR [ohm]
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
-50
-100
-150
-200
U [V]
Wir tragen nun den Widerstand und den differentiellen Widerstand über der Spannung
auf (siehe Abbildung 6 und 7. Der differentielle Widerstand berechnet sich gemäß
1
dR = dU
= UI22 −U
.
dt
−I1
6
5.2. Sprungverhalten des Stromes bei der Tunneldiode. Der Messbereich des Strommessgerätes wurde nun auf 100 µA herabgesetzt und die Spannung erneut von Null
hochgeregelt. Dabei konnten wir ein Sprungverhalten des Stromes beobachten.
Im gewählten Messbereich beträgt der Innenwiderstand des Strommessgerätes Ri =
1700 Ω. Dadurch ergeben sich drei Schnittpunkte der Arbeitsgeraden mit der Kennlinie
der Tunneldiode. Wird die Stromstärke von Null langsam hochgeregelt, so springt sie
beim Erreichen des ersten Schnittpunktes sofort auf den Wert des letzten Schnittpunktes. Zwischen den Schnittpunkten wählt die Stromstärke also den Weg der Arbeitsgeraden. Anschließend verläuft sie wieder entlang der Kennlinie.
5.3. Oszilloskopische Beobachtung der Spannung der Tunneldiode. Wir haben
dem Schaltkreis nun eine Spule hinzugefügt, so dass beim “Springen“ des Stromes
eine Spannungsüberhöhung statt fand. Die Spannung an der Tunneldiode haben wir
dann oszillosgraphisch beobachtet und dabei die Spannung am Spannungsteiler hochgeregelt.
In dem Augenblick in dem die Spannung den ersten Arbeitspunkt erreicht, fällt der
Strom sehr schnell ab. Dadurch erzeugt die Spule eine gegengerichtete Induktionsspannung. Somit springt die Spannung der Tunneldiode beim Erreichen des ersten Arbeitspunktes in den negativen Bereich. Anschließend baut sich die induzierte Spannung wieder ab und die Spannung der Diode läuft wieder entlang der Kennlinie zum
Arbeitspunkt. Beim Erreichen des Arbeitspunktes wiederholt sich der Vorgang. Dadurch entsteht ein periodische Schwingungsverhalten. Es kann also somit aus einer
Gleichspannung am Eingang nur mit Hilfe einer Diode und einer Spule eine Wechselspannung erzeugt werden.
7