6.2 Elektrischer Stromkreis a) b) n folgt aus den Daten von Kupfer

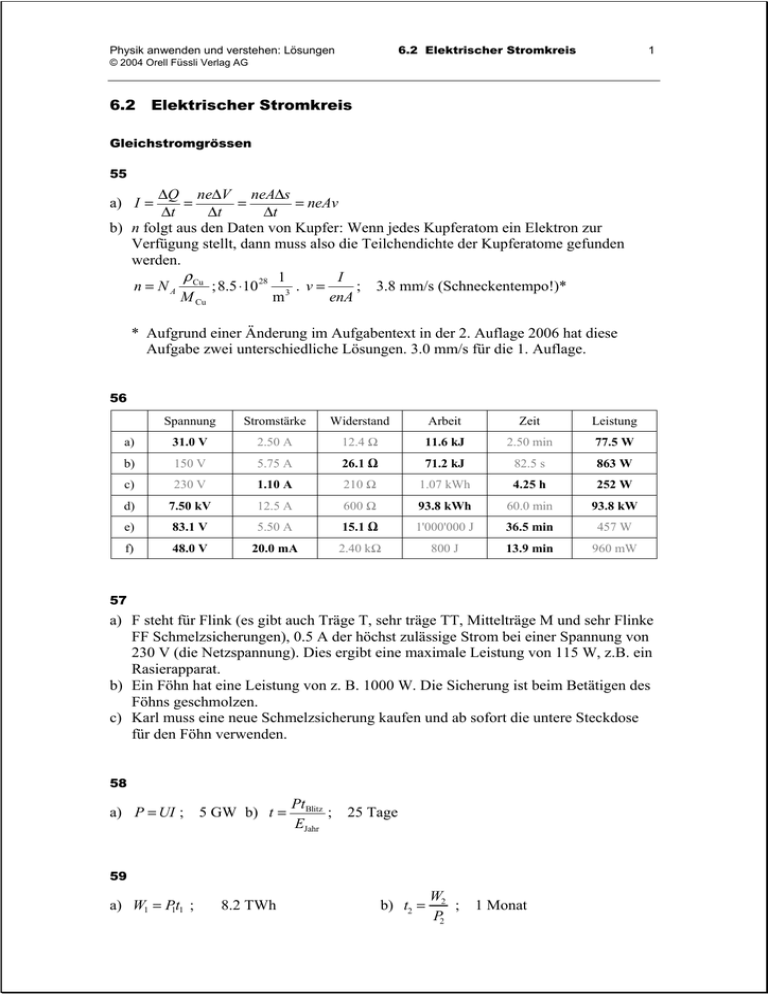
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
1
© 2004 Orell Füssli Verlag AG
6.2
Elektrischer Stromkreis
Gleichstromgrössen
55
∆Q ne∆V neA∆s
=
=
= neAv
∆t
∆t
∆t
b) n folgt aus den Daten von Kupfer: Wenn jedes Kupferatom ein Elektron zur
Verfügung stellt, dann muss also die Teilchendichte der Kupferatome gefunden
werden.
ρ
I
1
; 3.8 mm/s (Schneckentempo!)*
n = N A Cu ; 8.5 ⋅10 28 3 . v =
M Cu
m
enA
a) I =
* Aufgrund einer Änderung im Aufgabentext in der 2. Auflage 2006 hat diese
Aufgabe zwei unterschiedliche Lösungen. 3.0 mm/s für die 1. Auflage.
56
Spannung
Stromstärke
Widerstand
Arbeit
Zeit
Leistung
a)
31.0 V
2.50 A
12.4 Ω
11.6 kJ
2.50 min
77.5 W
b)
150 V
5.75 A
26.1 Ω
71.2 kJ
82.5 s
863 W
c)
230 V
1.10 A
210 Ω
1.07 kWh
4.25 h
252 W
d)
7.50 kV
12.5 A
600 Ω
93.8 kWh
60.0 min
93.8 kW
e)
83.1 V
5.50 A
15.1 Ω
1'000'000 J
36.5 min
457 W
f)
48.0 V
20.0 mA
2.40 kΩ
800 J
13.9 min
960 mW
57
a) F steht für Flink (es gibt auch Träge T, sehr träge TT, Mittelträge M und sehr Flinke
FF Schmelzsicherungen), 0.5 A der höchst zulässige Strom bei einer Spannung von
230 V (die Netzspannung). Dies ergibt eine maximale Leistung von 115 W, z.B. ein
Rasierapparat.
b) Ein Föhn hat eine Leistung von z. B. 1000 W. Die Sicherung ist beim Betätigen des
Föhns geschmolzen.
c) Karl muss eine neue Schmelzsicherung kaufen und ab sofort die untere Steckdose
für den Föhn verwenden.
58
a) P = UI ; 5 GW b) t =
PtBlitz
; 25 Tage
EJahr
59
a) W1 = Pt
11 ;
8.2 TWh
b) t2 =
W2
; 1 Monat
P2
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
2
© 2004 Orell Füssli Verlag AG
60
Nutzbarer Energieinhalt der Batterie: ∆E = UI ∆t ; 11.3 kJ;
Preis pro kWh also 790.– Fr.
Vergleich: 1 kWh aus dem Netz kostet ca. 20 Rappen.
61
1Fr. ⋅ 3.6 ⋅106 J/kWh
∆t =
= 2 ⋅106 s oder 25 Tage
0.14 Fr./kWh ⋅12 W
62
∆Q cm∆ϑ
=
; 3.3 min
P
P
U U2
b) R = =
; 59 Ω
I
P
c) P′ = 1 P ⇒ t ′ = 4t ; 4-mal länger
4
a) t =
63
a) ϑ2 = ϑ1 +
IU ∆t
; 56 °C
mc
b) η =
cm∆ϑ
; 86 %
IU ∆t
64
a)
Q
= L f + cAl ∆ϑ ; 0.97 MJ/kg bzw. 0.27 kWh/kg
m
Also 0.97 MJ um ein Kilogramm Aluminium auf Schmelztemperatur zu bringen und
dann noch zu schmelzen.
b) Aluminium ist 3fach positiv geladen.
In 110 Öfen wird in der Zeit t folgende Masse abgeschieden:
N
It
m = 110nAl M Al = 110 Al M Al = 110
M Al
NA
3eN A
In derselben Zeit wird folgende Arbeit aufgewendet:
W = Pt = UIt
3UeN A
W 3UIteN A
=
=
; 43 MJ/kg, bzw. 12 kWh/kg
m 110 ItM Al 110M Al
Also 43 MJ um ein kg Aluminium elektrolytisch zu gewinnen.
Es braucht also rund 44-mal mehr Energie, um Aluminium elektrolytisch zu
gewinnen, als es wieder einzuschmelzen!
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
© 2004 Orell Füssli Verlag AG
Serien- und Parallelschaltung
65
a) P = 20 ⋅ 4 '000 kWh = 250 kW
40 ⋅ 8 h
b) PL = P ; 12 W
n
66
RL
= RL I ; 20.9,
Rtot
U
somit dürfen 20 Glühbirnen parallel geschaltet werden.
a) N ist die Anzahl Glühbirnen: N =
2
b) P = 20 ⋅ U ; 1.32 kW (bei 20 Glühbirnen)
RL
67
a)
vor dem getrennten Streckenabschnitt:
auf dem getrennten Streckenabschnitt:
nach dem getrennten Streckenabschnitt:
T
b) I =
U
;
RM + RS
T
0.22 A
68
a) Es gibt nur zwei Schaltungen:
b) Es gibt diese 4 Schaltungen:
3
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
4
© 2004 Orell Füssli Verlag AG
c) Es gibt die 4 Schaltungen von N = 3 mit einem Serie- oder Parallelwiderstand mehr,
also 8 Fälle plus die nachfolgenden 2:
d) Es gibt die 10 Schaltungen von N = 4 mit einem Serie- oder Parallelwiderstand
mehr, also 20 Fälle plus die nachfolgenden 4:
e) Es gibt die 24 Schaltungen von N = 5 mit einem Serie- oder Parallelwiderstand
mehr, also 48 Fälle plus die nachfolgenden 18 Fälle:
Übrigens: (alles mit Computerhilfe gefunden)
N 1 2 3 4
# 1 2 4 10
5
24
6
66
7
180
8
522
9
10
11
1532 4624 14136
12
43930
13
137908
14
437502
Eine allgemeine Formel ist dem Autor dieser Aufgabe nicht bekannt, fragen Sie mal
Ihre Mathematiklehrerin bzw. Ihren Mathematiklehrer.
69
I1 = 220 mA , I 2 = 220 mA , I 3 = I 4 = 73.3 mA
70
a) 10 Ω
b) I1 = 2.4 A , I 2 = 1.4 A , I 3 = I 4 = 0.96 A , I 5 = 0.58 A , I 6 = 0.86 A
c) 20 V
71
a) Lösung des Gleichungssystems P1 = 300 W =
P2 = 1250 W =
U2
b) P =
;
R
U2
bzw.
R1 + R2
U 2 ⋅ ( R1 + R2 )
ergibt R1 = 71 Ω und R2 = 106 Ω.
R1 ⋅ R2
500 W bzw. 750 W
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
5
© 2004 Orell Füssli Verlag AG
72
U2
R
Stufe 1: R = 416 Ω, P = 130 W
Stufe 2: R = 255 Ω, P = 210 W
Stufe 3: R = 169 Ω, P = 310 W
Stufe 4: R = 86 Ω, P = 620 W
Stufe 5: R = 57 Ω, P = 930 W
Stufe 6: R = 50 Ω, P = 1.1 kW
a) allgemein: P =
b)
A wird verbunden mit
1
2
4
B wird verbunden mit
4
4 und 5
5
R
671 Ω
71 Ω
502 Ω
P
79 W
740 W
110 W
73
3-stufig
4-stufig
P1
R2
P2
R3
R1
1.32
kW
0.66
kW
40 Ω
80 Ω
160 Ω
40 Ω 1.32 kW 80 Ω 0.66 kW 180 Ω
P3
R4
0.33 kW
0.29 kW 360 Ω
P4
∆Qmax ∆Qmin
400 kJ 100 kJ
0.15 kW 400 kJ 44 kJ
Der 4-stufige Haarföhn hat kaum Vorteile, da die neue vierte Stufe nur eine sehr
schwache Wärmeleistung hat.
74
I
A
I1
I2
A
B
D
V
C
Wenn man Amperemeter und Voltmeter austauscht, bekommt man die oben stehende
Schaltung.
Das Amperemeter hat einen sehr kleinen Widerstand, so ist I1 ≈ 0. Das Voltmeter hat
einen sehr grossen Widerstand, so fliesst praktisch kein Strom zwischen C und D, somit
ist auch I ≈ 0.
Das Amperemeter zeigt praktisch keine Stromstärke, und das Voltmeter zeigt ungefähr
die Quellenspannung der Schaltung an: ein bisschen weniger als 230 V.
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
© 2004 Orell Füssli Verlag AG
75
a)
R
U0 −UL
; 2.7 Ω
I
U
c) η = L ; 82 %
U0
b) R =
76
Der Widerstand R1 der grossen Glühbirne beträgt nach Herstellerangaben:
U2
; 353 Ω
R1 =
P
Für die kleine Glühlampe gilt: R2 = 6.8 Ω
Der Gesamtwiderstand der in Reihe geschalteten Lampen ist: Rtot = R1 + R2
Folglich fliesst durch beide Lampen eine Stromstärke von: I =
U
Rtot
Über der grossen Glühbirne liegt eine Spannung von: U 1 = R1 I = R1
U
Rtot
U2
Die Leistung der grossen Lampe ist demnach: P1 = U 1 I = R1 2 ;
Rtot
144 W
U2
Analog gilt für die kleine Glühbirne: P2 = R2 2 ;
Rtot
2.8 W
77
a) Die Spannung wird 1:1 geteilt, also 6 V.
b) Die Spannung wird 2:1 geteilt, also 8 V.
U2
U12
c) R =
; 12 Ω, P1 =
= 5.3 W
P
R
(dies ist mehr als die erlaubten 3 W, das Lämpchen leuchtet also heller und wird
bald durchbrennen),
P3 = P4 = 1.3 W
(dies ist weniger als die erlaubten 3 W, diese Lämpchen leuchten einfach weniger
hell).
6
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
© 2004 Orell Füssli Verlag AG
78
a)
Schaltung 2
Schaltung 1
4V
0.3 A
6V
0.2 A
4V
0.3 A
6V
0.2 A
Schaltung 4
Schaltung 3
4V
0.3 A
6V
0.2 A
4V
0.3 A
6V
0.2 A
b) Bei den Schaltungen 2 und 4 beträgt die Gesamtstromstärke 0.3 A, bei den anderen
Schaltungen 0.5 A. Die Leistung ist also bei 2 und 4 am kleinsten.
79


R2
R1 R2
 1 
x
=
a) R =
mit
= R1 
1 
R1
R1 + R2
 +1
x 
Es wird die Funktion f ( x) =
1
x
und g ( x) = 1 dargestellt.
=
1+ x 1
+1
x
7
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
8
© 2004 Orell Füssli Verlag AG
b) Ist ein Widerstand der Parallelschaltung null, so ist der Ersatzwiderstand null. Dies
entspricht einem Kurzschluss.
Ist ein Widerstand der Parallelschaltung unendlich (entspricht offenem Schalter!), so
ist der Ersatzwiderstand gleich dem anderen.
80
)
(
a) R1,2 = 1 RS ± RS2 − 4 RP RS ; R1 = 94.7 Ω und R2 = 5.28 Ω
2
b) Sei RP der Parallelwiderstand und RS der Seriewiderstand, dann folgt aus
RR
1
1
1
+
=
, dass RP = 1 2 , d.h. R1 + R2 muss R1 R2 teilen.
R1 R2 RP
R1 + R2
Dazu können Sie ein kleines Programm schreiben, das aus zwei Schleifen besteht.
In der äusseren Schleife wird R1 von 1 bis 150 hochgezählt und in der inneren R2
von 1 bis 150, wobei jedes Mal die Teilbarkeit geprüft wird. Dann finden Sie unter
anderen folgende Lösungen, die aber alle nicht sehr nahe an der Lösung a) sind.
c)
R1 in Ω R2 in Ω RP in Ω RS in Ω
72
9
8
81
90
10
9
100
110
11
10
121
81
Diese Schaltung heisst Brückenschaltung. Sie lässt sich mit den Kirchhoff’schen Sätzen
vollständig verstehen.
R1
R3
R5
A
B
R2
R4
82
a)
U1
Batterie 1
U2
Batterie 2
32 V
kurzgeschlossen
32 V
kurzgeschlossen
30 V
30 V
b) U3 = R3 I3 ;
27 V
Rtotal
bezüglich
wirksamer Batterie
64 Ω
60 Ω
–
I1
I2
500 mA – 400 mA
– 375 mA
500 mA
125 mA
100 mA
I3
100 mA
125 mA
225 mA
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
9
© 2004 Orell Füssli Verlag AG
Innerer Widerstand
83
Beim Drehen des Zündschlüssels (= Schliessen des Schalters) steigt die Stromstärke I0
stark an. Bedingt durch den Innenwiderstand der Batterie, führt dies zu einer starken
Abnahme der Klemmenspannung.
I0
Schalter
Scheinwerfer
Ri
Anlasser
84
U K = U 0 − Ri I ; 11.8 V, 10.2 V
85
a) Die Batterie hat einen inneren Widerstand, der in Serie zum Lämpchen geschaltet
ist. Wenn ein äusserer Widerstand Ra angeschlossen wird, ist die gemessene
Klemmenspannung kleiner als die Quellenspannung U0.
U
b) Ra = R1 = 1 ; 9.0 Ω
P1 = U1 I1 ; 1.44 W
I1
U − U1
; 3.0 Ω
c) Ri = 0
I1
U0
; 0.32 A;
U 2 = R1 I 2 ; 2.88 V; P2 = U 2 I 2 ; 0.92 W
d) I 2 = 1
21R +R 
 1
i
2

86
U K = U 0 − Ri I
U 0 = 4.7 V;
I max = 1.1 A und Ri = 4.3 Ω.
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
10
© 2004 Orell Füssli Verlag AG
87
 U0 

Ri 
 ≈ U 0 ⋅  1 −  , falls Ra Ri ;
a) U K = Ra ⋅ 
 Ri + Ra 
 Ra 
b)
lim U K = U 0 .
Ra →∞
UK
U0
Ri
Ra
88
a) P = UI ; ja
U −UK
b) Ri = 0
; 200 Ω
I
c) Die Leistung wird maximal für R = Ri. Bei einem Verbraucherwiderstand von 200 Ω
2
U0
U0
wäre die Stromstärke I =
, die Leistung also P = R ⋅
; 0.17 W.
R + Ri
( R + Ri ) 2
89
a) Vereinfachende Annahme: Der Lampenwiderstand ist unabhängig von der
Stromstärke.
6V
RBirne =
= 12 Ω
0.5 A
R ⋅ 4 ⋅U 0
; 5.1 V
U K = Birne
RBirne + 4 ⋅ Ri
U K2
b) P =
; 2.2 W
RBirne
90
a) R =
UK
;
I
b) I1 =
U1 − U K
;
R1
7.97 Ω;
R1 =
35.7 m;
U1 − U K′
;
I′
I2 = I − I1 ;
1.96 Ω
146 mA;
R2 =
c) Die beiden Batterien werden sehr verschieden belastet.
Zwischen den Batterien fliesst ein Ausgleichsstrom.
U2 −UK
;
I2
0.205 Ω
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
© 2004 Orell Füssli Verlag AG
91
U0
; 20 A, 12 A und 5.5 A
Ri + Ra
U K = U 0 − Ri I ; 40 V, 48 V und 55 V
I=
92
a) Die Spannung beträgt: U = 5000 ⋅U 0 = 750 V
RReihe = 5000 ⋅ R0 = 1250 Ω
Die 140 Reihenwiderstände sind noch parallel geschaltet: Rinnen =
Somit ist I =
RReihe
= 8.9 Ω
140
U
; 0.93 A.
R
( aussen + Rinnen )
b) Die Stromstärke in den einzelnen Elektrozyten ist 140-mal kleiner als die gesamte
Stromstärke:
I Reihe = I ; 6.6 mA
140
Somit wird der Aal von seiner eigenen Stromquelle nicht getötet.
Spezifischer Widerstand
93
2
l = Rπ r ; 46 m
ρel
94
Weil sein Volumen erhalten bleibt, muss seine Querschnittsfläche A auf ein Drittel
zurückgehen. Wegen R = ρel l verneunfacht sich sein Widerstand auf 18 Ω.
A
95
a) U = Ri
3
I max ; 3.8 V
4
b) I = U = UA ; 6.2 A
R ρell
96
cm∆ϑ
; 1.0 kW
∆t
ρ lP
c) A = el 2 ; 4.3 ⋅10−9 m 2
U
a) P =
b) I =
P
; 4.4 A
U
11
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
© 2004 Orell Füssli Verlag AG
97
2l
; 0.68 Ω
A
RKabelU 0
U2
b) U = U 0 −
, wobei RMotor = 0 ; 225 V
RKabel + RMotor
P0
a) RKabel = ρel
c) P1 =
U2
; 1.8 kW
RMotor
d) PKabel
(U − U )
= 0
2
RKabel
; 44 W
98
a) lDraht = 11.55 m ;
b) RDraht = ρel
lDraht
;
db
d=
P=
ρel PlDraht
bU 2
;
0.22 mm
U 02 RDraht
; 92 W
( Ri + RDraht ) 2
c) I Draht RDraht = U 0 − Ri ( I Draht + I Anlasser ) ;
I Draht = 4.0 A ;
P = 23 W
99
a) R = ρel,Cu
4l
;
2
πd Cu
3.6 Ω und m = ρCu
2
πd Cu
l ; 1.5 t
4
2
ρ el,Al
πd Al
; 7.5 mm, m = ρ Al
l ; 0.71 t
ρ el,Cu
4
b) d Al = d Cu
100
a) Widerstand eines Seils zwischen den Kreuzungsmasten: 34 mΩ;
PV = I 2 RSeil ⋅ 6 ; 810 kW
b) d = 2
A
π
; 51 mm; effektiv ist der Durchmesser grösser, da 2027 mm2 den
reinen Materialquerschnitt angibt.
c) ρel = R
A
;
l
3.6 ⋅10−8 Ωm
12
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
13
© 2004 Orell Füssli Verlag AG
101
a) Aus U = RI und R = ρ el
b)
l
und m = ρAl folgt l =
A
mU
;
Iρ el ρ
1.43 km
∆l 1  ∆m ∆U ∆I 
= 
+
+  ; 0.081 = 8.1%, also l = 1.43 km ± 0.12 km
l
2 m
U
I 
Temperaturabhängiger Widerstand
102
U
; 120 Ω. Der Widerstand von Metallen nimmt mit steigender Temperatur
I
zu. Der Draht der Lampe im Betrieb mit 24 V ist offensichtlich sehr heiss (>2000
°C), sonst würde er nicht so hell mit weissem Licht glühen.
a) R =
b)
25
Spannung in V
20
15
10
5
0
0
50
100
150
200
Stromstärke in mA
c) An jeder Lampe liegt eine Spannung von (230/16) V = 14.4 V. Bei dieser Spannung
beträgt die Stromstärke gemäss Diagramm 150 mA. Das ist auch die Stromstärke für
die Reihenschaltung. Der Gesamtwiderstand beträgt (230 V/0.15 A) = 1.53 kΩ.
103
a) 6 V·0.6 A = 3.6 W
Also «6 V/3.6 W» ist die korrekte Lampeninschrift.
b)
:
b = 0.56
Physik anwenden und verstehen: Lösungen
6.2 Elektrischer Stromkreis
14
© 2004 Orell Füssli Verlag AG
3
c) Aus P = UI ∞ T und R = U ∞ T folgt I ∞ U 5
I
b = 0.60
4
2
d) R = U ∞ U3 = U 5
I
U5
e) Aus d) folgt mit R ∝ T : T = T0
U in V
I in A
R in Ω
T in K
1.0
0.22
4.5
1.6 ⋅103
2.0
0.32
6.3
2.2 × 103
R
, T0 = 353 K, R0 = 1.0 Ω
R0
3.0
0.41
7.3
2.6 ⋅103
4.0
0.48
8.3
2.9 ⋅103
5.0
0.54
9.3
3.3 ⋅103
6.0
0.60
10
3.5 ⋅103
104
Es handelt sich um Kennlinien bei unterschiedlicher, aber jeweils konstanter
Temperatur. Bei 1 ist der Widerstand kleiner und die Temperatur tiefer als bei 2.
105
Bei 1 nimmt der Quotient U/I mit zunehmender Spannung ab. Das bedeutet, dass der
Ohm‘sche Widerstand mit zunehmender Temperatur abnimmt. 1 ist also die Kennlinie
des NTC-Widerstandes, 2 die des PTC-Widerstandes.
106
Nach Einstellung einer Spannung nimmt die Stromstärke zu, weil sich der Widerstand
aufheizt und daher besser leitet. Bei den ersten Messungen stellt sich ein Gleichgewicht
zwischen der elektrischen Leistung Pzu = UI und der durch Wärmeleitung, Konvektion
und Wärmestrahlung abgegebenen Leistung Pab = Q t ein. Dadurch wird auch die
Temperatur stabil und die Stromstärke steigt nicht weiter. Bei der letzten Messung
nimmt über längere Zeit die Stromstärke und damit die elektrische Leistung schneller zu
als die abgegebene Wärmeleistung. Bevor sich ein neues Gleichgewicht einstellen kann,
ist eine Temperatur erreicht, bei der der Widerstand schmilzt.
107
Die Spannung U0 der Spannungsquelle wird in der Serienschaltung aufgeteilt:
U 0 = U NTC + U Lampe
U NTC U Lampe
=
RNTC RLampe
Wenn nach dem Einschalten die Temperatur der beiden Widerstände durch die
elektrische Energiezufuhr steigt, nimmt RNTC ab und RLampe zu. Somit nimmt auch UNTC
ab und ULampe zu. Die Stromstärke in der Reihenschaltung kann sich auch verändern.
Aber offensichtlich nimmt sie kaum ab, sondern eher zu, so dass die Leistung der
Lampe P = U Lampe I mit steigender Temperatur zunimmt.
Die Teilspannungen sind proportional zu den Widerständen:
6.2 Elektrischer Stromkreis
Physik anwenden und verstehen: Lösungen
15
© 2004 Orell Füssli Verlag AG
108
a)
RGlüh
RGlüh
RGlüh
RNTC
RNTC
RNTC
b) Der NTC-Widerstand darf sich nicht stark aufheizen und der Strom, der durch ihn
fliesst, trägt nicht zur gewünschten Lichtproduktion bei. Im kalten Zustand hat der
Glühdraht einen viel kleineren Widerstand als der NTC-Widerstand. Dadurch fliesst
bei gleicher Spannung mehr Strom durch den Glühdraht. Die Leistung ist für den
Glühdraht höher, und er wird so heiss, dass er glüht. Aber auch dann ist sein Widerstand immer noch deutlich kleiner als der des NTC-Widerstandes.
c) Wenn ein Glühdraht durchbrennt, hat der verbleibende, kalte NTC-Widerstand
einen viel grösseren Widerstandswert als die übrigen, intakten Lampen. In der
Reihenschaltung entfällt also auf ihn ein grosser Teil der Netzspannung. Dadurch
heizt er sich auf, und sein Widerstandswert geht zurück. Parallel dazu geht auch die
Teilspannung, die auf ihn entfällt, zurück. Im Vergleich zu a) ist die Teilspannung
an der (defekten) Lampe und die Stromstärke wieder etwa gleich gross. Der NTCWiderstand ist heisser, aber nicht so heiss, dass er glüht.
d) Offensichtlich kann es vorkommen, dass die in c) beschriebenen Vorgänge zu einer
grösseren Stromstärke in der Serienschaltung führen. Das geschieht, wenn der
Widerstand des heissen NTC-Widerstandes in einer defekten Lampe kleiner als der
Gesamtwiderstand einer intakten Lampe ist. Bei mehreren durchgebrannten Lampen
kann es so zu einer Überhitzung der übrigen Lampen kommen, die dann auch
durchbrennen. Schliesslich kann es zu einer Überhitzung der Zuleitungen und
Verbindungsdrähte mit Brandgefahr kommen.