6.2.5 Zwei Kondensatoren parallel oder in Serie

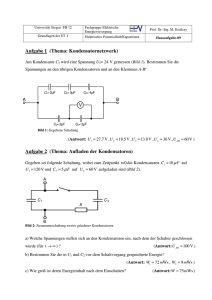
V060205
Zwei Kondensatoren parallel oder in Serie
6.2.5 Zwei Kondensatoren parallel oder in Serie
******
1 Motivation
Experimentelle Bestimmung der Kapazität zweier gleicher Kondensatoren in Serie- und in
Parallelschaltung.
2 Experiment
Abbildung 1: Zwei Kondensatoren parallel oder in Serie
Die Kapazität unterschiedlicher Anordnungen von Kondensatoren wird gemäss der Gleichung
C=
Q
U
(1)
bestimmt, wobei die Spannung U vorgegeben ist und die Ladung Q durch Entladen der Kapazitätsanordnung in einem ballistischen Galvanometer bestimmt wird (siehe Abb. 1).
Physikdepartement ETH Zürich
1
V060205
a
Zwei Kondensatoren parallel oder in Serie
C = C0
c
C = 2 C0
b
C=
C0
1
2
C0
C0
C0
C0
C0
Abbildung 2: Die drei Messanordnungen: a) Einzelkondensator, b) Parallelschaltung zweier
Kondensatoren, c) Serieschaltung zweier Kondensatoren.
Man misst mit drei verschiedenen Anordnungen (siehe Abb. 2):
a) Einzelne Kapazität C0 :
Die dabei gemessene Ladung
Q0 = C0 U
(2)
dient zur Normierung der folgenden beiden Messungen.
b) Parallelschaltung zweier Kondensatoren mit Kapazität C0 :
⇒
Q = 2Q0
C = 2C0
(3)
c) Serieschaltung zweier Kondensatoren mit Kapazität C0 :
Q = 21 Q0
⇒
Physikdepartement ETH Zürich
2
C = 12 C0
(4)
V060205
Zwei Kondensatoren parallel oder in Serie
3 Theorie
3.1 Das Gesetz von Gauss
Das Gesetz von Gauss folgt aus der Kombination des (rein mathematischen) Satzes von
Gauss und der (physikalischen) Maxwellgleichung, welche eine Beziehung zwischen Ladungen
und elektrischer Feldstärke herstellt.
Der Satz von Gauss führt ein Volumenintegral einer skalaren Grösse in ein Oberflächenintegral
eines Vektorfeldes über:
I
Z
(5)
E · dA = (∇ · E) dV ,
V
∂V
wobei ∂V die geschlossene Oberfläche des Volumens V bedeutet. Mit der Maxwellgleichung
(∇ · E) =
ρ
ε0
(6)
erhält man schliesslich das Gesetz von Gauss
Z
I
ρ
Q
dV =
ε0
ε0
E · dA =
(7)
V
∂V
Der Fluss des elektrischen Feldes aus einer geschlossenen Oberfläche heraus ist gleich der durch
die Oberfläche eingeschlossenen Ladung, dividiert durch die Dielektrizitätskonstante des Vakuums.
3.2 Elektrisches Feld und Kapazität des Plattenkondensators
Das elektrische Feld E im Innern steht senkrecht zur Platte (siehe Abb. 3); im Äussern ist es
annähernd gleich Null. Falls der Plattenabstand d verglichen mit den Plattendimensionen klein
ist, können wir annehmen, dass das Feld im Kondensator überall etwa gleich gross ist.Die Fläche
der Platte sei A.
Wir integrieren über die in der Figur gestrichelt eingezeichnete geschlossene Fläche O (Oberfläche
eines geeignet gewählten Quaders) und erhalten:
I
1
ΦE = En dA = E A =
Q
(8)
ε0
O
wobei Q die Ladung auf der Platte ist. Daraus ergibt sich sofort:
E=
=
1 Q
ε0 A
σ
,
ε0
wobei σ die Flächenladungsdichte ist (Einheit C m−2 ).
Physikdepartement ETH Zürich
3
(9)
(10)
V060205
Zwei Kondensatoren parallel oder in Serie
O
+Q
−Q
+
+
+
+
+
+
+
+
+
+
+
−
−
−
−
−
−
−
−
−
−
−
Abbildung 3: Das elektrisches Feld des Plattenkondensators. Randeffekte des Feldes sind vernachlässigt.
Die elektrische Spannung U zwischen den Platten beträgt
U = Ed =
1 Q
d,
ε0 A
(11)
wobei d den Plattenabstand bedeutet.
Für die Kapazität erhalten wir damit
C=
Q
A
= ε0
U
d
(12)
3.3 Kapazität zweier Kondensatoren
a) Parallelschaltung (siehe Abb. 4)
In diesem Fall liegt an beiden Kondensatoren dieselbe Spannung an, und die Ladungen
addieren sich:
Q = Q1 + Q2 = C1 U + C2 U
(13)
⇒
C = C1 + C2
Physikdepartement ETH Zürich
4
(14)
V060205
Zwei Kondensatoren parallel oder in Serie
+
−
C1
+
U
C1
C2
−
U
C2
Abbildung 4: Linkes Bild: Kondensatoren parallel. Rechtes Bild: Kondensatoren in Serie.
b) Serieschaltung
Zwischen den benachbarten Platten der beiden Kondensatoren kann die Ladung nur verschoben werden; deshalb muss sie entgegengesetzt gleich gross sein. Die Summe der an den
Kondensatoren abfallenden Spannung muss gleich der angelegten Spannung sein. Es gilt
also
Q
Q
U = U1 + U2 =
+
(15)
C1 C2
⇒
1
1
1
=
+
C
C1 C2
5
(16)