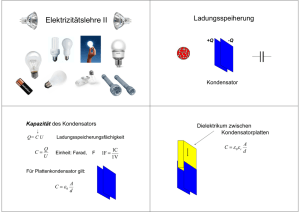
C Q C Q C Q + = 1 11 C CC + =

Zusammenschaltung von Kondensatoren
Hintereinanderschaltung:
Reihenschaltung zweier vorerst ungeladener Kondensatoren: Als Erweiterung der Kirchhoffschen
Knotenregel lässt sich angeben, dass die Summe aller nach dem Einschalten durch jeden Knoten der
Schaltung geflossenen Ladungen Null ist, da im Knoten keine Ladungen erzeugt oder vernichtet werden.
Nach dem Einschalten muss daher die Ladung auf beiden Kondensatoren gleich sein.
Aus der Maschenregel
U = U1 + U 2
bzw.
Q Q Q
=
+
C C1 C2
erhält man für die Gesamtkapazität der
Reihenschaltung:
1 1
1
=
+
C C1 C 2
Parallelschaltung:
Q = Q1 + Q2 .
C ⋅ U = C1 ⋅ U + C 2 ⋅ U . Daher gilt
Die gesamte Ladung ist die Summe der Ladungen auf den einzelnen Kondensatoren:
An beiden Kondensatoren liegt die selbe Spannung an, d.h.
C = C1 + C 2
Klammler
TPH 1
Seite 1 von 4
Laden und Entladen von Kondensatoren
Beim Laden und Entladen von Kondensatoren über ohmsche Widerstände erfolgt die Änderung des
Ladezustandes nicht sprunghaft; die Momentanwerte von Strom und Spannung ergeben sich aus den
Kirchhoffschen Regeln.
laden
R
I
Uq
entladen
C
Abbildung 1: Laden und Entladen eines Kondensators über einen ohmschen Widerstand
Laden:
Maschenregel:
Q
C
Uq = U R + UC = I ⋅ R +
Differentialgleichungen:
Ersetzen von I durch dQ/dt ergibt die Differentialgleichung
für Q(t):
Uq = R
dQ 1
+ Q
dt C
Oder man differentiert die Gleichung und erhält die
Differentialgleichung für I(t):
0=R
dI 1
+ I
dt C
Lösungen:
Ladestrom des Kondensators:
I (t ) = I 0 ⋅ e
−
t
RC
=
Uq
−
t
τ
⋅e
R
mit der Zeitkonstanten τ = R ⋅ C
Uq
Lösung der Differentialgleichung für die Ladung Q(t) am
Kondensator:
Q(t ) = Q0 ⋅ (1 − e
−
t
RC
−
U (t ) = U q ⋅ (1 −
Klammler
uc = U q (1 − e − t /τ )
t
τ
i=
) = U q ⋅ C ⋅ (1 − e )
Uq
R
e − t /τ
t
Mit U=Q/C beträgt damit die Spannung U(t) am
Kondensator:
t
−
e τ
Uq
R
Abbildung 2: Ladekurven
)
TPH 1
Seite 2 von 4
Entladen:
Maschenregel:
0 = U R + UC = I ⋅ R +
Q
C
Differentialgleichungen:
Differentialgleichung für Q(t):
0=R
dQ 1
+ Q
dt C
Differentialgleichung für I(t):
0=R
dI 1
+ I
dt C
Lösungen:
Entladestrom des Kondensators:
t
RC
t
−
U
= − 0 ⋅e τ
I (t ) = I 0 ⋅ e
R
mit der Zeitkonstanten τ = R ⋅ C .
−
U0
u c = U 0 ⋅ e −t /τ
− UR0
(U0...anfängliche Kondensatorspannung)
Ladung Q(t) am Kondensator:
Q (t ) = Q0 ⋅ e
−
t
RC
= U0 ⋅ C ⋅ e
−
t
τ
i=−
Abbildung 3: Entladekurven
Spannung U(t) am Kondensator:
U (t ) = U 0 ⋅ e
Klammler
−
U 0 −t / τ
e
R
t
τ
TPH 1
Seite 3 von 4
Energieinhalt des geladenen Kondensators
Um die Ladungsportion dQ entgegen der Kondensatorspannung auf den Kondensator zu laden, ist die
Arbeit
dW = U dQ zu verrichten. Mit C =
Kondensators
W = ∫ U dQ = ∫ U C du =
Q
U
bzw.
dQ = C dW beträgt die Arbeit zum Laden des
CU 2
.
2
Die Ladearbeit und damit der Energieinhalt des geladenen Kondensators beträgt daher
We =
CU 2
2
Diese Energie steckt im elektrischen Feld gespeichert. Wenn man die Energie durch das
We
. Mit der Formel für die Kapazität
V
We ε 0 E 2 D ⋅ E
=
=
. Dies ist eine allgemein gültige
des Plattenkondensators erhält man damit we =
V
2
2
Beziehung für die Energiedichte des elektrischen Feldes
& &
D⋅E
we =
2
Kondensatorvolumen dividiert, erhält man die Energiedichte
Klammler
TPH 1
we =
Seite 4 von 4