Versuch M08: Auf- und Entladung von Kondensatoren I Einleitung

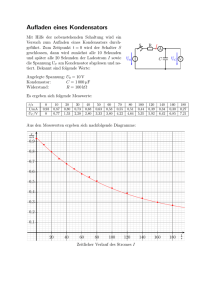
Versuch M08: Auf- und Entladung von
Kondensatoren
16. April 2014
I Einleitung
I.1
Exponentieller Aufbau und Zerfall
Thema dieses Versuches ist das exponentielle Zeitverhalten, wie es bei der
Auf- und Entladung eines Kondensators über einen Widerstand auftritt. Das
in diesem Versuch untersuchte
monoexponentielle Zeitverhalten ist von
genereller Bedeutung, das nicht nur in elektrischen Schaltkreisen, sondern
auch bei Phänomenen der radioaktiven Zerfälle, Lebensdauern angeregter
Zustände von Atomen und Molekülen, Populationsdynamiken in der Biologie, Reaktionen erster Ordnung in der Chemie u.a. eine wichtige Rolle spielt.
Dierentialgleichung erster Ordnung beschrieben, bei der die erste Ableitung der
In diesen Fällen ist das Zeitverhalten des Prozesses durch eine
gemessenen Gröÿe nach der Zeit immer proportional zu dieser Gröÿe selbst
ist, nämlich:
1
dA(t)
= − · A(t) + E,
dt
τ
(1)
A(t) die gemessene Gröÿe ist, während E ein Eingangssignal bedeutet.
Die Konstante τ wird als Zeitkonstante bezeichnet. Für sinusförmige Eingangssignale ist A(t) ebenfalls sinusförmig. (Dieser Fall spielt bei Versuchen
wobei
im Bereich Elektronik eine Rolle.)
Für ein Eingangssignal
E=0
E , das sich zur Zeit t = 0 sprungartig von E = A0 auf
A(t) durch die Exponentialfunktion
ändert, ist das Zeitverhalten von
t
A(t) = A0 · e− τ
beschrieben. Springt das Eingangssignal
E = A0 ,
E
zur Zeit
(2)
t = 0
von
E = 0
auf
so gilt:
t
A(t) = A0 · 1 − e− τ .
1
(3)
Gleichung (2) beschreibt den exponentiellen Abbau oder die Entladung
A0 ), während Gleichung (3) den Aufbau oder
die Aufladung von Null bis zum Endwert A0 wiedergibt. Aufgrund der
sprungartigen Änderung von E zum Zeitpunkt t = 0 wird A(t) in Gleichun(beginnend beim Anfangswert
gen (2) und (3) auch als
I.2
Sprungantwort bezeichnet.
Messung der Kondensatorentladung
Abbildung 1: Zur Aufnahme der Entladefunktion
Wird ein Kondensator der Kapazität
so folgt die Spannung
UC
C
über einen Widerstand
R
entladen,
am Kondensator der Entladungsgleichung:
t
UC = U0 · e− RC .
Zunächst wird die Kondensatorspannung
U0 = 10 V
(4)
mit Hilfe des Voltme-
ters exakt eingestellt. Dann trennt man die Kabelverbindung
K und startet
exakt zu diesem Zeitpunkt die Stopp-Uhr. Unter scharfer Beobachtung der
Spannungsanzeige und mit Hilfe der Split-Funktion der Stopp-Uhr lassen
sich jetzt sehr genaue Wertepaare von Spannung und Zeit aufnehmen.
I.3
Messung der Kondensatoraufladung
Hierzu dient die Messschaltung nach Figur 2, wobei lediglich die eine Leitung des Kondensators umgelegt werden muss. Für den Aufladevorgang des
Kondensators
C
über den Widerstand
2
R
gilt die Aufladegleichung:
t
UC = U0 · 1 − e− RC .
(5)
Abbildung 2: Zur Aufnahme der Aufladefunktion
Zunächst wird der Kondensator mit dem Kabel
nung
U0 = 10 V
K überbrückt und die Span-
wieder mit Hilfe des Voltmeters exakt eingeregelt. Genau
im Moment der Trennung der Kabelbrücke startet der Aufladevorgang des
UC ergibt
U + UC = 10 V.
Kondensators. Die gesuchte Kondensatorspannung
abgelesenen Wert
U
aus
UC = 10 V − U ,
3
da
sich mit dem
II Aufgaben
1.) Bestimmen Sie den Zeitverlauf der Kondensatoraufladung und -Entladung jeweils für 2 selbst ausgewählte
nungssprung
10 V.
RC -Kombinationen für den Span-
Zur freien Auswahl stehen je 4 Kondensatoren und
Widerstände zur Verfügung:
C/µF
1
2,2
4,7
10
R/MΩ
1
2,21
4,75
10
Die Fehlertoleranz der einzelnen Bauteile beträgt 1% für die Widerstände und 5% für die Kondensatoren. Mit Hilfe der Zeitkonstante
R·C
τ
=
lässt sich der erforderliche Zeitaufwand pro Messbereich abschät-
zen, was man bei der Versuchsplanung berücksichtigen sollte.
2.) Stellen Sie die 4 Zeitverläufe der Sprungantwort
U (t)
grasch auf zwei
Bögen DIN A4 Millimeterpapier dar, wobei für jede RC-Kombination
Auf- und Entladung gemeinsam auf demselben Blatt dargestellt sind.
3.) Entnehmen Sie den Graken die sogenannten Halbwertszeiten
tH ,
das sind die Zeiten, bei denen die Spannung 50% des Spannungsendwertes erreicht hat.
t
auf (warum?). Tragen Sie
RC
U
für die Kondensatorauf- und Entladung ln
über der Zeit auf (U ist
U0
dabei jeweils die gemessene Spannung). Zeichnen durch die jeweiligen
4.) Lösen Sie die Gleichungen 4 und 5 nach
Messpunkte die Ausgleichsgeraden und bestimmen aus den Steigungen
der 4 Geraden die Zeitkonstanten
τ.
5.) Berechnen Sie die zu erwartenden Zeitkonstanten aus der Formel
RC .
Ri = 100 MΩ des
1 MΩ), der dem jeweils
Hierbei muss der Innenwiderstand
berücksichtigt werden (Oszilloskop:
ten Widerstand
R
τ =
Voltmeters
ausgewähl-
parallel geschaltet ist, wohingegen der Innenwider-
stand der Gleichstromquelle vernachlässigbar gering ist.
6.) Vergleichen und diskutieren Sie die Ergebnisse von 3, 4 und 5.
4