docx

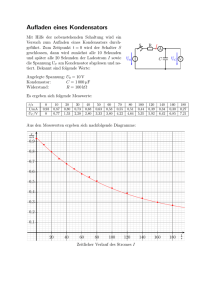
Entladen eines Kondensators im
mathematischen Modell
Nach dem Laden des Kondensators ( 𝐶 = 100 ∙ 10−6 𝐹) wird der Schalter umgelegt und
der Kondensator entlädt sich über den Widerstand R = 470.000 Ω. Zum Zeitpunkt t =
0s liegt also am Kondensator die Spannung 𝑈𝑎𝑙𝑡 = 12𝑉 an.
Nach dem Ohmschen Gesetz fließt dann ein Strom der Stromstärke
(1)
𝐼 = 𝑈𝑎𝑙𝑡 /𝑅
I ist definiert als Ladungsmenge, die pro Zeit (ab-)geflossen ist, also ergibt
sich für die abgeflossene Ladungsmenge 𝛥𝑄 . . .
(2)
∆𝑄 = 𝐼 ∙ ∆𝑡
(1) in (2) eingesetzt ergibt für die in der Zeit ∆𝑡 geflossene Ladung ∆𝑄 . . .
(3)
∆𝑄 =
𝑈𝑎𝑙𝑡
𝑅
∙ ∆𝑡
𝑄
Da der Kondensator Ladung „verloren“ hat, sinkt nach 𝐶 = 𝑈 die Spannung (C
ist konstant für den Kondensator!) um den Wert ∆𝑈. Es ist . . .
(4)
∆𝑈 =
∆𝑄
𝐶
(3) in (4) eingesetzt ergibt dann
(5)
∆𝑈 =
𝑈𝑎𝑙𝑡
𝑅∙𝐶
∙ ∆𝑡
Die Spannung 𝑈𝑎𝑙𝑡 = 12𝑉 ist in der Zeit ∆𝑡 also um den Wert ∆𝑈 =
𝑈𝑎𝑙𝑡
𝑅∙𝐶
∙ ∆𝑡
gesunken. Es errechnet sich somit neben der Koordinate K1 (t1=0s; 12V) die
zweite Koordinate zu K2 (∆𝑡; 𝑈𝑎𝑙𝑡 −
noch die Spannung Uneu = Ualt -
𝑈𝑎𝑙𝑡
𝑅∙𝐶
𝑈𝑎𝑙𝑡
𝑅∙𝐶
∙ ∆𝑡 ). Jetzt liegt am Widerstand nur
∙ ∆𝑡 an. Diesen Wert setzt man nun für Ualt
in Gleichung (1) ein und kann damit K3 errechnen.
Aufgabe 1
Vervollständigen Sie durch Rechnung untenstehende Tabelle und trage die Messwerte
in das Diagramm ein.
Aufgabe 2
Bauen sie obige Schaltung auf und bestimmen sie die Messwerte UG experimentell
und diskutieren Sie mögliche Abweichungen vom mathematischen Wert.