Entladekurve eines Kondensators Aufgabe: Nehmen Sie die

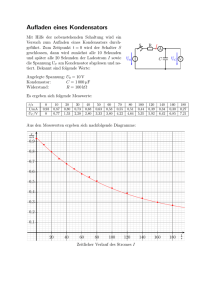
Entladekurve eines Kondensators
Aufgabe:
Nehmen Sie die Entladekurve eines Kondensators auf und ermitteln Sie daraus die im Kondensator
gespeicherte Ladung und dessen Kapazität!
1. Bauen Sie folgende Schaltung auf. Achten Sie unbedingt auf die Polung des Kondensators.
2. Stellen Sie am Stromversorgungsgerät eine Spannung von 9 V ein.
3. Entladen Sie den Kondensator über den Widerstand R=10 kΩ. Messen Sie nach jeweils 5 s die
Stromstärke.
4. Berechnen Sie mit Hilfe der Formel R=U/I die zu erwartende Anfangsstromstärke. Begründen Sie
Abweichungen zu ihrer gemessenen Anfangsstromstärke.
5. Stellen Sie die Entladekurve I(t) graphisch dar und geben Sie die Gleichung an. (exponentielle
Regression, I in A)
6. Die Fläche unter dem Graphen I(t) entspricht der vom Kondensator gespeicherten Ladung. Ermitteln
Sie mit Hilfe der Regressionsgleichung aus Aufgabe 5 den Flächeninhalt und damit die gespeicherte
Ladung.
7. Führen Sie den Versuch für zwei weitere Ladespannungen (3V und 6V) durch und ermitteln Sie jeweils
die gespeicherte Ladung.
8. Stellen Sie die Ladung in Abhängigkeit von der Spannung graphisch dar. Welcher Zusammenhang
besteht? Begründen Sie. Geben Sie die Gleichung der Kurve an.
9. Die Kapazität des Kondensators wird nach der Gleichung C=Q/U berechnet. Berechnen Sie die
Kapazität des Kondensators aus den drei Messwertpaaren. Berechnen Sie den Mittelwert und geben Sie
diesen in μF an. Wie lässt sich die Kapazität im Diagramm aus Aufgabe 8 interpretieren?
10. Nennen Sie je zwei systematische und zufällige Fehlerquellen.