14. Energie des Kondensators im Spulenfeld: Deduktive Herleitung:
Werbung
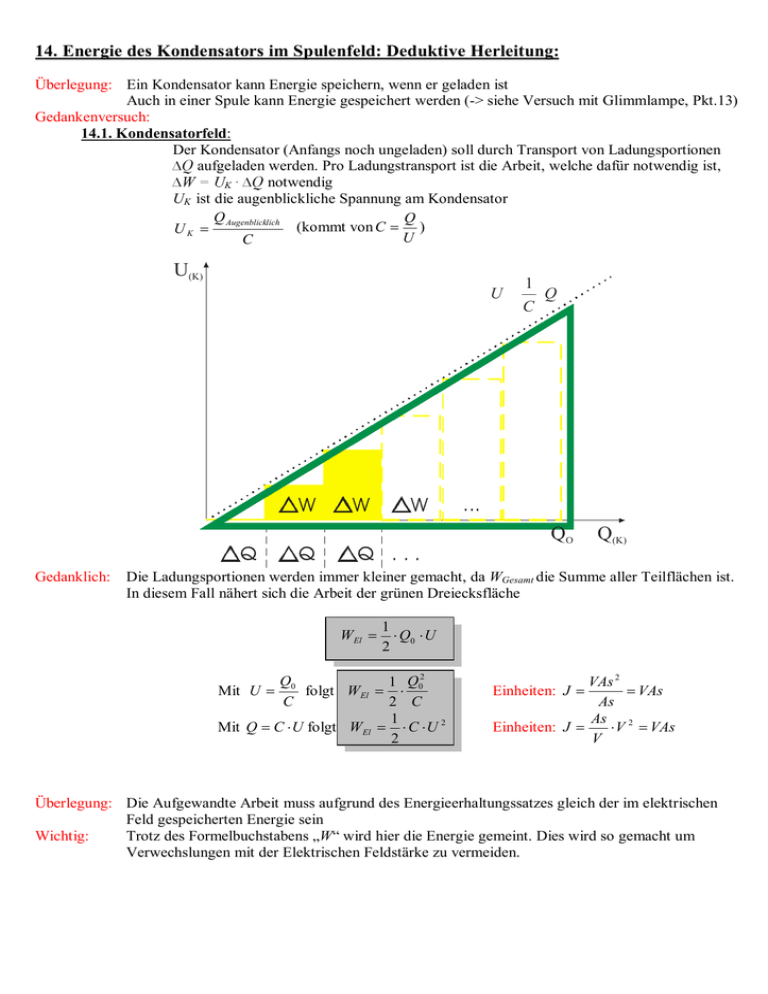
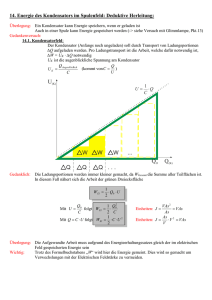
14. Energie des Kondensators im Spulenfeld: Deduktive Herleitung: Überlegung: Ein Kondensator kann Energie speichern, wenn er geladen ist Auch in einer Spule kann Energie gespeichert werden (-> siehe Versuch mit Glimmlampe, Pkt.13) Gedankenversuch: 14.1. Kondensatorfeld: Der Kondensator (Anfangs noch ungeladen) soll durch Transport von Ladungsportionen aufgeladen werden. Pro Ladungstransport ist die Arbeit, welche dafür notwendig ist, notwendig K UK ist die augenblickliche Spannung am Kondensator Q Augenblicklich Q (kommt von C = ) UK = U C U(K) U 1 Q C QO Gedanklich: Q(K) Die Ladungsportionen werden immer kleiner gemacht, da WGesamt die Summe aller Teilflächen ist. In diesem Fall nähert sich die Arbeit der grünen Dreiecksfläche WEl = 1 ⋅ Q0 ⋅ U 2 Q0 1 Q02 Mit U = folgt WEl = ⋅ 2 C C 1 Mit Q = C ⋅ U folgt WEl = ⋅ C ⋅ U 2 2 VAs 2 Einheiten: J = = VAs As As 2 Einheiten: J = ⋅ V = VAs V Überlegung: Die Aufgewandte Arbeit muss aufgrund des Energieerhaltungssatzes gleich der im elektrischen Feld gespeicherten Energie sein Wichtig: Trotz des Formelbuchstabens „W“ wird hier die Energie gemeint. Dies wird so gemacht um Verwechslungen mit der Elektrischen Feldstärke zu vermeiden. 14.2. Spulenfeld: Analog zur Energie eines Kondensators gibt es auch die magnetische Energie eines Spulenfeldes Auch in Spulenfeldern muss Energie gespeichert werden können t Deduktive Herleitung: t W = ∫ U Ind ⋅ I ⋅ dt = ∫ − L ⋅ I ⋅ I ⋅ dt = 0 0 I (t ) durch Substitution: t dI ∫ L ⋅ dt ⋅ I ⋅ dt = 0 I = I (t ) Im ax 1 W = − ∫ L ⋅ I ⋅ dI = − ∫ L ⋅ I ⋅ dI = − ⋅ L ⋅ I 2 2 0 I (0 ) 0 => Wm = = 1 ⋅L⋅I2 2 1 ⋅L⋅I2 2 Aufgabe: S.111/ Nr.1 Berechnen Sie die Energie eines Plattenkondensators, dessen kreisförmige Platten einen Durchmesser von 26 cm und einen Abstand von 3,0 mm haben, wenn an den Platten eine Spannung von 4,7 kV liegt. (1,7 mJ) Lösung: C = ε0 A 1 ; W = CU ² => d 2 2 0,26m π ⋅ 1 A 1 2 2 −12 −1 −1 W = ⋅ ε ⋅ 0 ⋅ U ² = ⋅ 8,8542 ⋅ 10 CV m ⋅ ⋅ (4700V ) = 1,7mJ 2 d 2 0,03m