KAPAZITÄT und ENERGIE - Fakult at f ur Physik

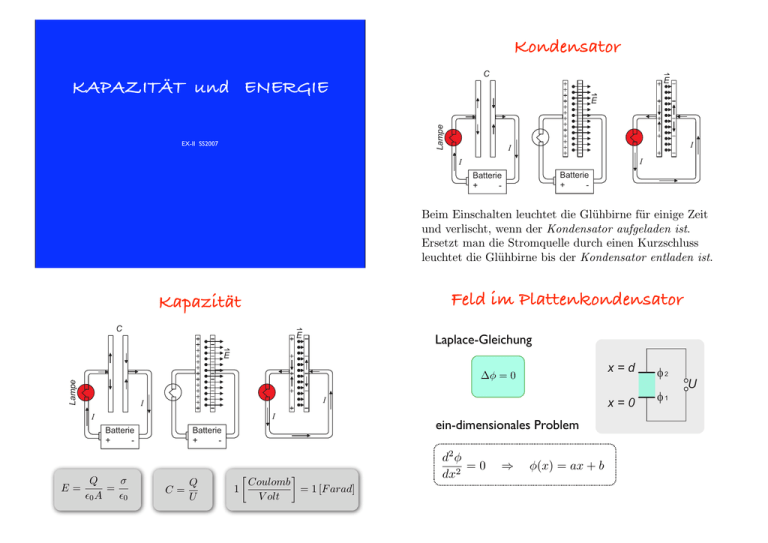
Kondensator
"
KAPAZITÄT und ENERGIE
!
# $ % & '
!
EX-II SS2007
!
!
!
!
! " ##$ % &$
' ((((((((()
! " ##$ % &$
' ((((((((()
Beim Einschalten leuchtet die Glühbirne für einige Zeit
und verlischt, wenn der Kondensator aufgeladen ist.
Ersetzt man die Stromquelle durch einen Kurzschluss
leuchtet die Glühbirne bis der Kondensator entladen ist.
Feld im Plattenkondensator
Kapazität
"
Laplace-Gleichung
!
!
# $% $&
∆φ = 0
# $ % & '
!
!
!
!
!
Q
σ
=
!0 A
!0
C=
Q
U
1
!
# $% $"
ein-dimensionales Problem
! " ##$ % &$
' ((((((((()
! " ##$ % &$
' ((((((((()
E=
! "!
"
Coulomb
= 1 [F arad]
V olt
d2 φ
=0
dx2
⇒
φ(x) = ax + b
! ""
"
Feld im
Plattenkondensator
# $% $&
! "!
!
2
d φ
=0
dx2
φ(x) = ax + b
⇒
! "
# $% $"
Randbedingungen
φ(x) =
φx=0 = φ1 = b
φx=d = φ2 = ad + φ1
! "!
!
"
! "
"
U
x + φ1
d
# $% $"
C=
Kondensatoren
"
Beispiel:
für A = 1 cm2 und d = 1 mm ist C = 0.9 pF .
1 Volt
σ
Q
U
=
=
"0
"0 A
d
A
d
Kapazitätsbereiche :
# $% $&
! = −∇φ
! = − U !ex
E
d
E=
C = !0
Feld im
Plattenkondensator
C = !0
A
d
Q
U
Q=CU
≈ 5 × 106 Elektronen
Feld einer geladenen Hohlkugel
Homogene Verteilung der Ladung - Symmetrie des Problems
pF, nF, µF, mF
Hohlkugel trägt die
Flächenladungsdichte σ.
!
! "#
$
Gesamtladung: Q = 4πR2 σ
%
! ·E
! = 1ρ
∇
"0
' (
&
!
S
&
$
#
Für Kugelfläche r < R gilt
)
"
' (
&
! · dS
!=0
E
#
$
&
"
Kapazität eines Kugelkondensators
%
U = φi − φa = fc Q
$
&
$
'
C=
Q
r
Feldstärke springt um σ/"0
#"
!
1
1
−
ri
ra
"
$
$
Q
ri
φ(r) = fc
%
Potentialdifferenz
Zwei konzentrische Hohlkugeln
mit den Radien ri und ra
tragen die Ladungen +Q und −Q.
φi = fc
Kapazität eines Kugelkondensators
#"
ri ≈ R ≈ ra
C=
$
! "
1 R2
A
= !0
fc d
d
Schaltung von
Kondensatoren
Kapazität einer Kugel
'
Q
1 ri · ra
Q
=
=
U
φi − φa
fc ra − ri
! "
! > ri ) = fc Q êR
E(r
r2
$
&
C = !0
A
d
parallel:
gleiche Spannung liegt an der Summe der Flächen
Wenn wir den Radius der äußeren Kugel
gegen ∞ anwachsen lassen
Cges =
!
Ci
i
C=
Q
1 ri · ra
Q
=
=
U
φi − φa
fc ra − ri
ri = R
in Serie:
Die gleiche Ladungsdifferenz (jeweils +Q und −Q )
verteilt sich über die Summe der Abstände.
ra → ∞
C = 4π"0 R
1
Cges
=
! 1
Ci
i
+Q −Q
+Q −Q
+Q −Q
geladene Kugel als Energiespeicher
Spannungsüberhöhung
φR = fc
φ∞ = 0
Die Ladung verteilt sich auf den Kondensator und das Elektrometer
!
! "
dW = dQ (φR − φ∞ ) = dQ φR
Qges = QC + QE = CE · UE + CC · UC
$
Differenz der potentiellen Energie
Qges = (CE + CC ) · U
Wenn wir d erhöhen und
damit die Kapazität CC erniedrigen,
dann steigt die Spannung U an!
!
!
"
#
1
W = fc
R
!
Q dQ =
1
Q2
1 Q2
·
=
4π"0 R 2
2 C
Energiespeicher
Wel =
UE = UC = U
Energiedichte im Plattenkondensator
"
C = !0 A/d
!
#
1 Q2
1
= CU 2
2 C
2
Energiedichte
Gilt für beliebige elektrische Feldanordnungen im Vakuum.
Definition der Energiedichte des elektrischen Feldes :
U =E·d
wel = Wel /V =
Volumen des Kondensators A · d = V
Wel =
1
1
1
C U 2 = !0 E 2 · Ad = !0 E 2 V
2
2
2
Energiespeicher
Wel =
Volumen &
elektrisches Feld
1 Q2
1
= CU 2
2 C
2
Wel =
1
!0 E 2
2
1
1
1
C U 2 = !0 E 2 · Ad = !0 E 2 V
2
2
2
[wel ] =
W ·s
J
= 3
3
m
m
"
!
Q
R
Besondere Vorsicht ist bei Arbeiten mit Hochspannung angebracht. Verkabelungen sollten vor Inbetriebn
von einer zweiten Person geprüft werden. „Stolperdrähte“ sind zu vermeiden. Es sind nur Verkabelunge
hochspannungstauglichen Kabeln und Steckern, welche entsprechend isoliert sind, zugelassen.
Versuchsaufbauten mit blanken Drähten oder hochspannungsfreien Stellen sind verboten. Die Verkabelu
sind übersichtlich zu halten. Der Erdung ist besondere Beachtung zu schenken. Lieber einmal zu viel als
zu wenig kompetente
Hilfe beiziehen.
DieStromschlages
Werkstatt hilft lieber beim Verkabeln, als dass sie nachher def
Gefährlichkeit
eines
Geräte flickt! Zudem sind Arbeiten mit Hochspannung zu unterlassen, wenn sich nur eine Person im Lab
5 mA spürt man
als unangenehm,
befindet, insbesondere nachts und an<Wochenenden.
Vorsicht:
auch nach Ausschalten des Geräts liegt ma
> 50 an
mA
frieren Nervensignale
undmit
Muskeln
ein
für einige Zeit noch eine hohe Spannung
(Kondensator).
Dauerversuche
Hochspannung
sind für D
klar zu kennzeichnen mit Namen und Erreichbarkeit.
Kraft zwischen Kondensatorplatten
"
1
wel = Wel /V = !0 E 2
2
!
Sicherheitsaspekte
Innenwiderstand des menschlichen Körpers
Platten sind entgegengesetzt geladen (+Q und −Q)
Sie ziehen sich mit einer Kraft F an
1
F ∆d = !0 E 2 A ∆d
2
Kraft x Weg
Zunahme des
Volumens
30 Volt
1
1
F = !0 E 2 · A = Q · E
2
2
Widerstand trockener Haut (≈ 20kΩ)
Der Hautwiderstand kann aber bei hohen
Spannungen bis auf Null absinken.
σ
Q
E=
=
"0
"0 A
Bereich
1:
Wechselströme in diesem Bereich werden von den meisten Menschen
gar nicht wahrgenommen.
Bereich
2:
Es ist ein Kribbeln zu spüren, auch schmerzhafte Verkrampfungen
sind möglich. Direkte Schäden sind kaum zu befürchten.
Bereich
3:
Die Stromquelle kann auf Grund von Muskelverkrampfung nicht mehr
losgelassen werden.
Bereich
4:
Schwere Schädigung und häufig tödliche Stromwirkung , z.B. durch
Herzkammerflimmern.
Stromweg
Körperwiderstand
(minimal)
Hand Hand
ca. 650 "
Hand Fuß
ca. 1300 "
Hand Füße
ca. 975 "
elle
u
Hände gsq"
un650
n
ca.
n
a
p
Füße
!
er S
ng d esentlich beträgt
Leistu DerisHautwiderstand
tw
einige Tausend Ohm, kann
bei hohen Spannungen aber
bis auf Null absinken.
,-. /,0+#12" -1'13# .3%#$'2*+45
Jeder Mensch lädt sich durch Bewegung schnell mal auf mehrere 1000V auf. Oft reichen wenige Volt Sp
aus, aktive elektrische Bauteile zu zerstören. Dies kommt auch schon mal vor, wenn man mit der Hand o
Berührung in die Nähe des Bauteils kommt.
Beim Arbeiten mit hochempfindlichen Messgeräten oder elektrischen Bauteilen aller Art ist grundsätzlic
Erdungsband zu tragen. Das einfache Tragen eines Erdungsbandes verhindert teure Reparaturarbeiten.
!"#$ % &'()"*+,"(!"##$ %&'($ )&'* +&,-. /'* '&01-) &)- 21'$ +&,-&(3$&-4 5##$&' *&$ %2)&)
6501-. *57 $&' %&'( 3$&' +&,- &)-89
Grundsätze zum Umgang mit Chemikalien:
! Keine Stoffe verwenden, wo ich mir über die Giftigkeit nicht
im Klaren bin.
! Sicherheitshinweise auf den Etiketten beachten!
! Kapellen benutzen
Chemikalien mit sehr giftigen, giftigen o
gesundheitsschädlichen Eigenschaften
T+
T
Xn
Chemikalien mit ätzenden oder reizende
Eigenschaften
C
Xi