Elastischer Stoß mit einem ruhenden Körper

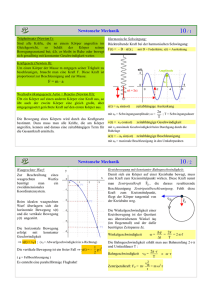
Elastischer Stoß eines sich bewegenden Körpers auf einen ruhenden Körper
1. Wir stellen uns zunächst unter m eine kleine und unter M eine große Masse vor.
Die Geschwindigkeit der stoßenden Masse m sei v, die große Masse ruht.
m
v
M
m
Nach dem Impulserhaltungssatz gilt:
Nach dem Energieerhaltungssatz gilt:
(1)
(2)
u1
M
u2
m v = m u1 + Mu2
½ m∙v2 = ½ m∙u12 + ½ M∙u22
M
u
m 2
Setzt man diesen Term für u1 in die mit 2/m multiplizierte Gleichung (2) ein, erhält man zunächst
Aus Gleichung (1) ergibt sich
(1')
u1 = v -
(2')
M ö
M
æ
v 2 = ç v - u2 ÷ + u12
m ø
m
è
2
éæ M
ù
ö
0 = u2 × êç + 1 ÷ u2 - 2v ú ,
ø
ëè m
û
und nach einigen Umformungen die Gleichung
welche die beiden Lösungen für u2 u2 = 0 oder u2 =
2m
× v besitzt, zu denen nach (1') die Lösungen für u1
M+m
M-m
× v gehören.
M+m
Die Lösung [u1 = v und u2 = 0] beschreibt den Fall, dass die (kleine) Masse m die (große) Masse M nicht trifft.
u1 = v oder u1 = -
M-m
2m
Nach einem elastischen Stoß haben die beiden Körper die Geschwindigkeiten u1 = - M + m × v und u2 = M + m × v .
99
2
× v » - v und u2 =
×v »0
101
101
Überprüfe die Gültigkeit des Impulserhaltungssatzes und des Energieerhaltungssatzes für dieses Beispiel:
2. Die Ergebnisse für M = 100∙m : u1 = -
IES:
EES:
3. Vertauscht man M und m in der oberen Herleitung, die an keiner Stelle die Voraussetzung M > m benutzt, so
gewinnt man für den elastischen Stoß einer (großen) Masse M der Geschwindigkeit v auf eine ruhende (kleine)
Masse m
M
v
m
M-m
M
u1
m
u2
2M
die Gleichungen u1 = M + m × v und u2 = M + m × v .
4. Die Ergebnisse für M = 100∙m : u1 =
99
200
× v » v und u2 =
× v » 2v
101
101
Überprüfe die Gültigkeit des Impulserhaltungssatzes und des Energieerhaltungssatzes für dieses Beispiel:
IES:
EES:
5. Zum Schluss formulieren wir das Ergebnis allgemeiner
für beliebige Massen m1 und m2 , von denen m1 zunächst
die Geschwindigkeit v hat und m2 zunächst ruht:
u1 =
m1 - m2
2m1
× v und u2 =
×v
m1 + m2
m2 + m 1