Computational Neuroscience Das Neuron

Computational Neuroscience
Das Neuron
http://www.nefo.med.uni-muenchen.de/~vorlesung/
Inhalt
• Neuronenarten
• Ionenkanäle
• Ruhemembranpotential
• Ersatzschaltbild
• Aktionspotentialleitung
• Modellierung der Funktion (Hodgkin-Huxley)
Literatur / Referenzen
Bücher
• Kandell, Schwartz: Principles of Neural Science
• Dayan, Abbott: Theoretical Neuroscience
• Gerstner, Kistler: Spiking Neurons
• Feynman: Lectures on Physics
• Bower und Beeman: Book of Genesis
Links
• http://www.nefo.med.uni-muenchen.de/~vorlesung/
• http://www.genesis-sim.org/GENESIS/
Neuron:
Unterschied zu anderen Zellen
Schnelle Membranpotentialänderung
• Ruhemembranpotential: -65 mV
(bezüglich extrazellulärem Raum)
• Aktionsmembranpotential: bis +55 mV
• 500 V/s, bis 108 Ionen/s/Kanal
⇒Signalverarbeitung:
⇒Signale sind Membranpotentialänderungen
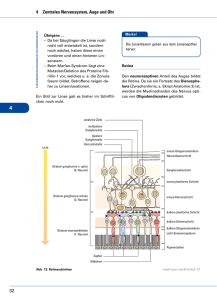
Neuronenarten
Neuronenarten
Neuron: Funktion
Signalentstehung und –weiterleitung
im (Knie-) Reflexbogen
Zellmembran als Isolator
Ionen im
polaren Wasser
Na+, Cl-
Lipid-Doppelschicht:
Nichtpolar
Vm=Vin-Vex
VR=-60 ...-70 mV
K+, A-
Geometrie der Zellmembran
(Kung 2005, Nature 436)
Membrangeometrie beeinflußt die intrinsischen Kräfte
Ionenkanäle
Grund für Mebranpotentialänderung: Ionenkanäle
Funktionen der Ionenkanäle:
1. Ionenleitung
2. Ionenselektion (Na+ vs K+)
3. Öffnen / Schließen (Schalten)
in Abhängigkeit von folgenden Siganalen:
• Elektrisch (Spannung)
• Mechanisch (Druck, Spannung)
• Chemisch (Transmitter)
Ionenkanal: Selektivität
R=0,095 nm
=> ENa stark, mehr H20
R=0,133 nm
=> EK schwach, weniger H20
Ionenkanal: Selektivität
für K+, Na+, Mg2+, Ca2+, Cl-
Aktive Zone
Kompensation für den
Verlust der energetisch
günstigen H2O-Wolke
durch polare Aminosäuren
Ionenkanal: Schalter
non-gating
gating
Chemisch
(Transmitter)
Resistiv
(Ohmsch)
Gleichrichter
(nichtlinear)
Elektrisch
Mechanisch
Ionenkanal: Schaltfunktion
(Sigworth 2003, Nature 423)
Ionenkanal: Struktur
(McKinnon 2005, Science 309)
(Kung 2005, Nature 436)
Ionenkanäle: Phylogenese
(Kung 2005, Nature 436)
Ruhemembranpotential
Nernst-Potential für K+
[ ]
[ ]
20 mM
R ⋅T
K+ O
⋅ ln + = 26 mV ⋅ 2,3 ⋅ log10
= −75 mV
Ek =
400 mM
Z ⋅F
K I
Nernst-Potential für Na+
[ ]
[ ]
440 mM
R ⋅T
Na + O
Ek =
⋅ ln
=
26
mV
⋅
2
,
3
⋅
log
= +55mV
10
Z ⋅F
Na + I
50 mM
R: Gaskonstante 8,314 J/mol.K
F: Faradaykonstante 9,65.104 C/mol
Exkurs: Nernst-Potential
Zustandsgleichung
des idealen Gases
P ⋅V = N ⋅ k ⋅ T
N
⇒ P = ⋅ k ⋅T = n ⋅ k ⋅T
V
⇒ dP = Px + Px + dx = k ⋅ T ⋅ dn
BoltzmannVerteilung
Druck
Ort x
nx+dx
Px+dx
(Ideal gas law)
x+dx
F ⋅ n ⋅ dx = Px + Px + dx = dP
x
=
k ⋅ T ⋅ dn
F ⋅ n ⋅ dx
Fdx dn
=
kT
n
dP.E. dn
−
=
kT
n
1
1
P.E.
.
.
−
=
⇒
−
= ln n + c
dP
E
dn
∫n
kT ∫
kT
∆U
P. E .
−
−
(
)
n
x
1
⇒
= e kT
n( x ) = n0 ⋅ e kT
n( x 2 )
∆U = k ⋅ T ⋅ ln
n2
n1
∆U =
nx
Px
F
Kraft im
Potential
P.E.: Potentielle
Energie
R ⋅T M o
ln
Z ⋅ F Mi
(Feynman, Vol I, 40-2)
Na+-K+-Pumpe
Aufrechterhaltung der Ionengradienten
durch Energiezufuhr (Metabolismus – ATP)
Kanal: Batterie mit Widerstand
Ersatzschaltbild
(Electrical equivalent circuit)
Ek =
[ ]
[ ]
R ⋅T
K+
20 mM
⋅ ln + O = 26 mV ⋅ 2,3 ⋅ log10
= −75 mV
Z ⋅F
K I
400 mM
Ersatzschaltbilder
für mehrere Ionenkanäle
Ruhemembranpotential (Vm):
Berechnung mit Ersatzschaltbild
− I Na = I K
⇒ I Na + I K = 0
Vm = ENa +
I Na
g Na
Vm = EK +
IK
gK
⇒ I Na = g Na ⋅ (Vm − ENa )
⇒ I K = g K ⋅ (Vm − EK )
⇒ Vm ⋅ ( g Na + g K ) = (ENa ⋅ g Na ) + (EK ⋅ g K )
⇒ Vm =
Vm =
(ENa ⋅ g Na ) + (EK ⋅ g K )
(g Na + g K )
ENa ⋅ g Na + EK ⋅ g K + ECl ⋅ gCl
= −69 mV
(g Na + g K + gCl )
(De- und Hyper-) Polarisierung
Dynamik: Sprungantwort
U=
Q
C
Ic = C ⋅
⇒ dU =
dQ I c ⋅ dt
=
C
C
dU
dt
dU m
dt
−t


U m (t ) = I m Rin ⋅ 1 − e Rin ⋅Cin =τ 


I m = I i + I C = Rin ⋅ U m + Cin ⋅
meuler.m
1
T
N
u
t
=
=
=
=
4;
T/dt;
zeros(N,1);
linspace(0,T-dt,N)';
i = zeros(N,1);
i(t>.2) = 1;
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.5
1
1.5
2
Zeit [s]
2.5
3
3.5
4
1
Spannung [V]
dt = 0.01;
C = 1;
g = 1;
Strom [A]
0.8
0.8
0.6
0.4
0.2
0
u(1) = 0;
for j=2:N
u(j) = u(j-1) + dt/C * (i(j-1) - g * u(j-1));
end;
subplot(211), plot (t, i, 'k-');
ylabel ('Strom [A]');
set (gca, 'YLim', [-.1 1.1]);
subplot(212), plot (t, u, 'k-');
xlabel ('Zeit [s]');
ylabel ('Spannung [V]');
set (gca, 'YLim', [-.1 1.1]);
du (t ) 1
= [I (t ) − g ⋅ u (t )]
dt
C
du (t ) u j − u j −1
=
dt
∆t
u j − u j −1 1
= [i j −1 − g ⋅ u j −1 ]
C
∆t
∆t
u j = u j −1 + [i j −1 − g ⋅ u j −1 ]
C
Einfache Simulink-Simulation
U=
Q
C
Ic = C ⋅
⇒ dU =
dQ I c ⋅ dt
=
C
C
dU
dt
Im = Ii + Ic =
dU m
1
⋅ U m + C in ⋅
Rin
dt
du(t )
= I (t ) − g ⋅ u (t )
dt
1
u (t ) = ⋅ ∫ (I (t ) − g ⋅ u (t ))dt
C
C
1
Sine Wave
Sign
1
s
Integrator
0.5
1
1/C
u
0
1
g=1/R
u
Sum
-0.5
To Workspace
-1
0
5
10
15
Time [s]
20
25
Ersatzschaltbild
Voltage Clamp
Voltage Clamp
http://www.science.smith.edu/departments/NeuroSci/courses/bio330/squid.html
K- und Na-Leitfähigkeit: Dynamik
Inaktivierung der Na-Leitfähigkeit
Aktionspotential
(Hodgkin, Huxley and Katz 1952, Hodgkin and Huxley 1952a-d)
Nobelpreis 1963
Filme
Kennzahlen
• Spezifische Membrankapazität: ~1µF/cm2
• Ruhemembranpotential: Urest~-70mV
• Spezifischer Ruhewiderstand: 1M
mm2
• Membranoberfläche ca.: 0.01-0.1 mm2
• Membrandicke: 3-4 nm
Hodgkin-Huxley-Modell
I (t ) = I cap (t ) + ∑ I k (t )
k
I cap (t ) = C ⋅
= I (t )
du
dt
− ∑ I k (t )
k
6444444444474444444444
8
3
4
− g Na m h ⋅ (u − E Na ) + g K n ⋅ (u − E K ) + g L ⋅ (u − E L )
m& = α m (u ) ⋅ (1 − m ) − β m (u ) ⋅ m
n& = α n (n ) ⋅ (1 − n ) − β n (u ) ⋅ n
h& = α (u ) ⋅ (1 − h ) − β (u ) ⋅ h
[
]
h
x
x
E x (mV )
Na
K
L
115
-12
10,6
(
g x mS
)
cm
120
36
0,3
n
2
m
h
h
(
)
α x u mV
0,1 − 0,01u
e1−0,1u − 1
2,5 − 0,1u
e 2,5−0,1u − 1
0,07 ⋅ e
−u
20
(
β x u mV
0,125 ⋅ e
4⋅e
−u
−u
)
80
18
1
e 3−0,1u + 1
Hodgkin-Huxley-Modell
Kaliumstrom: gK n4 (u(t)-EK)
n& = α n (u ) ⋅ (1 − n) − β n (u ) ⋅ n
Gating-Variable n beschreibt den
Übergang einer Gating-Untereinheit
(activation particle) vom offenen in
den geschlossenen Zustand und
zurück.
Wahrscheinlichkeit für “offen”: n
Wahrscheinlichkeit für
“geschlossen”: 1-n
1
α
0.9
β
0.8
transitions (1/s)
0.7
Das Öffnen von 4 unabhängigen und
identische Gating-Untereinheiten ist
erforderlich um einen Kaliumkanal zu
öffnen → n4.
0.6
0.5
0.4
0.3
0.2
0.1
0
-100
-80
-60
-40
-20
0
u (mV)
20
40
60
80
100
α beschreibt die
spannungsabhängige Übergangsrate
vom geschlossenen zum offenen
Zustand (β offen → geschlossen)
Hodgkin-Huxley-Simulation
Iinj/Am
in nA/cm^2
u/(Am*(1-b))
Pulse
Generator Iinj
Fläche
1
s
Integrator
Vm
Scope Vm
iIons
iIons
Vm
Sum
dVm (t )
C⋅
= I (t ) − ∑ I k (t )
dt
k
⇒ Vm (t ) =
1 

⋅ ∫  I (t ) − ∑ I k (t ) dt
C 
k

in mV
Hodgkin-Huxley-Simulation
Iinj/Am
in nA/cm^2
u/(Am*(1-b))
Pulse
Generator Iinj
Vm
Fläche
gkm*(Vm-Vk0)
IK
iK
-K-
Vm gNam*(Vm-VNa0)
I Na
1
s
1/cm Integrator
Vm
Scope Vm
in mV
iNa
Vm
I Ions = ∑ I k (t ) = I Na + I K + I L
k
IL
To Workspace
gL*(u-VL0)
um.mat
iL
To File
Sum
3
4
(
)
(
)
I
t
=
g
m
h
⋅
V
−
E
+
g
n
⋅ (Vm − E K ) + g L ⋅ (Vm − E L )
∑ k
Na
m
Na
K
k
Hodgkin-Huxley-Simulation
Vm
1
Vm
Iinj/Am
gK*(u^4)
n
in nA/cm^2
n^4
u/(Am*(1-b))
n(Vm)
1
gkm*(Vm-Vk0)
Pulse
Generator Iinj
Fläche
-62
EK
Vm
Vm-EK
gkm*(Vm-Vk0)
Product
iK
-K-
1
s
1/cm Integrator
Vm gNam*(Vm-VNa0)
I K = g K n ⋅ (Vm − E K )
Vm
Scope Vm
in mV
iNa
Vm
4
To Workspace
gL*(u-VL0)
um.mat
n ∈ [0 K1] =) [0K100%]
(
⇒ gK n
4
)
iL
mS
mS
4
= 36 2 ⋅ n (Vm , t ) ∈ [0 K 36] 2
cm
cm
To File
Sum
Hodgkin-Huxley-Simulation
Vm
n
1
Vm
gK*(u^4)
n^4
n(Vm)
1
gkm*(Vm-Vk0)
-62
EK
n
Vm-EK
Product
1-u
0,1 − 0,01 ⋅ V
α n (Vm ) = 1−0,1⋅Vm m
e
−1
1
(1-n)
a_*(1-n)
f(u)
u-Vr
Vm
(0.01*(10-u))
/(exp((10-u)/10)-1)
V
Product
Sum1 Integrator1
V
0.125*exp(-u/80)
−Vm
1
n
b_n*n
f(u)
β n (Vm ) = 0,125 ⋅ e
1
s
Product1
n
80
n = ∫ [α n (Vm ) ⋅ (1 − n ) − β n (Vm ) ⋅ n]dt
Hodgkin-Huxley-Simulation
Vm
gK*(u^4)
n
1
Iinj/Am
n^4
Vm
in nA/cm^2
n(Vm)
u/(Am*(1-b))
1
gkm*(Vm-Vk0)
Pulse
Generator Iinj
Fläche
-62
EK
Vm-EK
Vm
gkm*(Vm-Vk0)
Product
iK
1
s
Integrator
Vm
Vm
Scope Vm
in mV
gNam*(Vm-VNa0)
iNa
n
Vm
To Workspace
1-u
gL*(u-VL0)
(1-n)
a_*(1-n)
iL
f(u)
1
Vm
u-Vr
(0.01*(10-u))
/(exp((10-u)/10)-1)
V
Sum
Product
1
s
Sum1 Integrator1
V
b_n*n
f(u)
0.125*exp(-u/80)
Product1
n
1
n
neuron_init.m
Am= 3.14e-4
Cm = 1
% total membrane area [cm^2]
% area specific membrane capacitance [µF/cm^2)
VK0
VL0
VNa0
Vr
%
%
%
%
Nerst potential
Nerst potential
Nerst potential
membrane steady
%
%
%
%
area
area
area
area
gJ
gK
gNa
gL
= -62
= -39.4
= 65
= -50
= 700
= 36
= 120
=
0.3
specific
specific
specific
specific
K+ ions [mV]
other ions [mV]
Na+ ions [mV]
state voltage
conductance
conductance
conductance
conductance
of
of
of
of
the junction seal [µS/cm^2]
K+ ion channels [µS/cm^2]
Na+ ion channels [µS/cm^2]
other ion backgroud channel [µS/cm^2]
h0=0.5961
m0=0.0529
n0=0.3177
b=0.1
mK=0
mNa=0
mL=0
%
%
%
%
ratio between junction membrane area to total membrane area
µK activity of K+ ion channels on junction membran [0=0%, 1=100%, 2=200%]
µNa activity of Na+ ion channels on junction membran [0=0%, 1=100%, 2=200%]
µL activity of other ion channels on junction membran [0=0%, 1=100%, 2=200%]
Simuliertes Aktionspotential
60
Membranpotential [mV]
40
20
0
-20
-40
-60
0
5
10
Zeit [ms]
15
Leitungseigenschaften
rm
=
λ=
ra
λ=
∆V ( x ) = ∆V0 ⋅ e
−x
λ
Rm
ρ
2πa
πa 2
Rm a
⋅
ρ 2
λ
Längenkonstante
Rm
spez. Membranwiderstand
ρ
spez. Cytoplasmawiderstand
a
Radius
Weiterleitung eines
Aktionspotentials
Myelinisierung
1− 2mm
2 µm
πa 2
1
v~
=
c m ⋅ ra c m ρ
Fragen
• Ersatzschaltbild einer Membran
• Berechnung des Ruhemembranpotentials
• Differentialgleichung der passiven Membran
• Sprungantwort / Simulink-Modell
• Funktionsweise der Voltage Clamp
• Getrennte Messung der K- und Na-Ströme
• Dynamik der K- und Na-Ströme
• Qualitative Beschreibung eines Aktionspotentials
• Hodgkin-Huxley-Gleichung
• Bedeutung der Gating-Variablen n, m, h
Exkurs: Skalarprodukt (1)
WANTED
r r
Eine mathematis che Operation a , b für die zwei Pfeile
r
r
bzw. Vektoren a und b mit folgenden Eigenschaf ten :
(1)
( 2)
(3)
( 4)
r r
r r
k ⋅ a, b = k ⋅ a, b
r r
r r
a, b = b , a
r r r
r r
r r
a + c , b = a, b + c , b
1, falls i =
r r
ei , e j = 
0, falls i ≠
1
 0
r a 
r
r
a =  1  = a1 ⋅   + a 2 ⋅   = a1 ⋅ e1 + a 2 ⋅ e2
 0
1
 a2 
r b 
1
 0
r
r
b =  1  = b1 ⋅   + b2 ⋅   = b1 ⋅ e1 + b2 ⋅ e2
0
1
 b2 
r r
a+c
r
a
Kommutativ gesetz
Distributivgesetz
j
 = δ (i, j )
j
r
e2
r r
r
r
r
r
a , b = a1 ⋅ e1 + a 2 ⋅ e2 , b1 ⋅ e1 + b2 ⋅ e2 mit (3)
r
r
r
r
r
r
r
r
= a1 ⋅ e1 , b1 ⋅ e1 + a1 ⋅ e1 , b2 ⋅ e2 + a 2 ⋅ e2 , a1 ⋅ e1 + a 2 ⋅ e2 , b2 ⋅ e2 mit (1)
r r
r r
r r
r r
= a1 ⋅ b1 ⋅ e1 , e1 + a1 ⋅ b2 ⋅ e1 , e2 + a 2 ⋅ b1 ⋅ e2 , e1 + a 2 ⋅ b2 ⋅ e2 , e2 mit (4)
r r
r r
⇒ a , b = a o b = a1 ⋅ b1 + a 2 ⋅ b2
r
a
r
c
r
b
r
e1
r r
a, b
r r
c,b
r r r
a + c, b
Rechenregel für 2D
Exkurs: Skalarprodukt (2)
r
r r
r r
r
a , b = a ⋅ b ⋅ cos(ϕ ) = a ⋅ cos(ϕ ) ⋅ b
r
a
r
e2
r
b
ϕ
r
e1
r
a ⋅ cos(ϕ )
Cosinussatz
B
r
a
ϕ
C
r
c
r
b
A
r r
r r
r
r
b , a = b ⋅ a ⋅ cos(ϕ ) = b ⋅ cos(ϕ ) ⋅ a Kommutativ gesetz (2)
r r
a, b
cos(ϕ ) = r r
b⋅a
r r r
∆ABC : c = a − b
r2 r r2
r r r r
c = a −b = a −b ⋅ a −b
r2 r2
r r
= a + b − 2⋅a ob
r2 r2
r r
= a + b − 2 ⋅ a ⋅ b ⋅ cos(ϕ )
(
)(
)
r2 r2 r2
für ϕ = 90° gilt : c = a + b (Pythagora s)
Perceptron
S1
wi1
S2
wi2
Neuron i
Σ
win
n
oi = ∑ S j w ji
Sn
j =1
Skalarprodukt in n Dimensionen
zwischen Signalvektor S und
Vektor der synaptischen Gewichte wi
Neuron 1
w11
Σ
S1
S2
w21
Σ
w1n
Sn
w2n
Neuron 2
...
Neuron m
r
r
o =W ⋅s
 o1   w11
  
 o2   w21
O = 
  
o   w
 m   m1
w12
w22
w1n   s1 
  
  s2 
 ⋅ O
O
  
wmn   s n 
Skalarprodukt: Anwendung 1
Korrelationskoeffizient
r=0.83
35
x=1:8;
a=x+randn(size(x));
b=4*x+randn(size(x));
az=(a-mean(a))./std(a);
bz=(b-mean(b))./std(b);
r=az*bz'/length(x);
30
25
20
b
ra ,b
~
1 n
1 n a i − a~ bi − b 1 r r
= ⋅ ∑ z (ai ) ⋅ z (bi ) = ⋅ ∑
⋅
= ⋅ a z o bz
σb
n i =1
n i =1 σ a
n
15
10
plot(a,b,'ko');
xlabel('a');
ylabel('b');
title(sprintf('r=%1.2f',r));
5
0
1
2
3
4
5
6
7
8
a
a =
b =
r =
1.3986
4.2914
0.8322
3.1163
9.1071
3.6205
12.2450
3.7123
16.1650
3.6282
20.4062
5.3141
25.2160
7.3317
29.4484
7.0023
30.9749
Skalarprodukt: Anwendung 2
Fouriertransformation
Purkinje-Zelle als Perceptron
(Brunel et al., 2004)
Exkurs: Infinitesimalrechnung
df ( x )
f (x + h ) − f (x )
= lim
dx
h
h →0
Differentiation
Differentialquotient
f(x)=x
3
Beispiele:
2
⇒
 ( x + h )2 − x 2 x 2 + 2 xh + h 2 − x 2

df ( x )
= lim 
=
= 2 x + h = 2 x
dx
h
h
h→ 0 

f (x ) = e x
⇒
 e x+h − e x
eh −1
de x
1 − 1
x
= lim 
= ex
= ex
=e
h
h 
dx
h
h →0 
f (x ) = x
f(x+h)
f(x)
x
x+h
Integration
h ⋅ f ( x + h ) ≥ A(x + h ) − A(x ) ≥ h ⋅ f (x ) ÷ h
A(x + h ) − A(x )
≥ f (x )
h
A(x + h ) − A( x )
⇒ lim
= f (x )
h
h →0
dA( x )
⇒
= f (x ) ⇔
∫ f (x )dx =A(x )
dx
f (x + h ) ≥
f(x)
A(x)
A(x+h)-A(x)
f(x)=x
3
f(x+h)
A(x+h)
x x+h
Integration ist Umkehrung der Differentiation
Ruhemembranpotential