Document

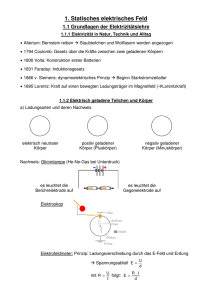
Biologische Physik 2
(Physik für Biologen)
Elektrostatik:
Ladungen - Arten, Wechselwirkung
Elektrisches Feld, Elektrische Feldstärke, Feldlinien
Elektrostatisches Potential, Äquipotentialflächen, Spannung
Plattenkondensator, Kapazität, Dielektrikum, Schaltung und
Anwendung von Kondensatoren
Gleichstrom:
Spannungsquellen, Strom, Spannung, Ohmsches Gesetz
Kirchhoffsche Gesetze und Gleichstromnetzwerke
Stromleitung in Flüssigkeiten, Stromleitung in Gasen und Vakuum
Elektrizität in Biosystemen
Etwas zur Geschichte:
Jahrhunderte hat sich in der Elektrizität nicht viel getan, dann aber ….
600 v. Chr.:
Erste Beschreibung der elektrostatischen Eigenschaften des
Bernsteins (Elektron) (Thales v. Milet)
1746
Pieter van Musschenbroek erfindet die "Leidener Flasche„
1749
Benjamin Franklin regt die Bezeichnungen "positiv" und
"negativ" für die Elektrizität an
1785
Charles de Coulomb stellt das "Coulomb'sche Gesetz„ auf
1786
Abraham Bennet erfindet das Goldblatt-Elektroskop
1787
Luigi Galvani führt seine "Froschschenkelexperimente" durch
1789
Alessandro Volta erklärt die Froschschenkelexperimente
(Funktionelle Elektrostimulation → Rehabilitation)
1910
Robert Millikan – Bestimmung der Elementarladung „e“
1987
Nobelpreis für Supraleitung (Verlustfreie Stromleitung)
Ladungen - Arten, Wechselwirkung
Die Elektrostatik:
Gesamtheit der Erscheinungen die von ruhenden Ladungen stammen
Wechselwirkung elektrisch geladener Körper
Seit dem Altertum ist bekannt, dass Körper sich durch reiben aufladen
können. Wo haben Sie sich schon „aufgeladen“ ?
Staub oder kleine Teilchen bleiben an aufgeladenen Körpern hängen. Sie
werden auch gegen die Gravitationskraft angezogen.
LADUNGEN – „entstehen“ z.B. durch Reibung
Es gibt mindestens zwei Arten von Ladungen ……………
Genaue Untersuchungen haben gezeigt, dass es genau zwei Arten von
Ladungen gibt.
Man benannte die Ladungen so, dass Ladungen auf geriebenen Glasstäben
positiv genannt werden und Ladungen auf geriebenem Bernstein negativ.
Ladungen sind nicht beliebig teilbar. Versuche von Millikan ergaben,
dass die kleinste beobachtbare Ladung den Betrag
e = 1.6022 x 10-19 C hat.
Wir nennen es ELEMENTARLADUNG e.
Was ist die Ladung von 1C ? → 1/e = 6,24 x 1018 Elementarladungen
Ladung ist somit gequantelt, ist auch verschiebbar und bleibt erhalten.
Elektron → kleinste negative Ladung
Proton → kleinste positive Ladung (Wasserstoffkern)
In Kernbauteilen, den Quarks, gibt es Ladungen vom Betrage e/3 . Diese sind
nicht frei zu beobachten.
Elektron - der Name kommt vom griechischen Wort Elektron und
bedeutet Bernstein, denn an ihm wurde die Elektrizität erstmals
beobachtet. Reibt man Bernstein beispielsweise mit einem Katzenfell, so
lädt es sich elektrisch auf
→ Reibungselektrizität
Manche Stoffe eignen sich besonders gut zur Leitung der
elektrischen Ladungen – man nennt sie elektrische Leiter.
Leiter (1. Klasse) sind Metalle. Die Leitfähigkeit von Metallen beruht auf
der Verfügbarkeit von beweglichen Ladungsträgern – Elektronen. Bei
einem Leiter können die Elektronen (in der „Aussenhülle“ mit wenig
Energie abgelöst werden, sie stehen dann zum Ladungstransport zur
Verfügung.
Unter einem Nichtleiter versteht man einen Festkörper, der nicht
elektrisch leitfähig ist. Nichtleiter bezeichnet man auch als Isolatoren oder
Dielektrika.
Nichtleiter sind Stoffe, deren Elektronen fest an die Atome gebunden sind
(z.B. Glas, Keramik, trockenes Holz, Kunststoffe oder reines Wasser).
Und … es gibt auch die Halbleiter ….
Unter einem Halbleiter versteht man einen Festkörper, dessen
elektrische Leitfähigkeit zwischen der eines Metalls und der eines Isolators
liegt.
Ladungen können z.B. mit ELEKTROSKOP gemessen werden.
Wie funktioniert es ?
Metalle sind sehr gute Leiter – freie Bewegung von Ladungen ist möglich –
Messteile der Elektroskope werden aus Metallen gebaut.
Wir beobachten hier:
a.Kraftwechselwirkung,
b.Ladungstransport – Ableitung zu anderen
leitenden Flächen – „Erdung“,
c.Neutralisation – die Verbindung von pos.
und neg. geladenen Elektroskopen nivelliert
den Ausschlag.
Ausmessen des Kraftfeldes mit einem geladenem Probekörper Coulomb‘sches Gesetz
• Geladener Körper mit Ladung Q1
• Probekörper mit Ladung Q2
im Abstand r
Experimente ergeben :
F ∝ Q1
F ∝ Q2
1
F∝ 2
r
Richtung der Kraftwirkung
(bei Kugeln) liegt auf der
Verbindungsgeraden
(Zentralkraft)
r r
Q1 ⋅ Q2
F (r ) = K ⋅
r2
Verhalten von Ladungen:
Die Kraft zwischen 2 Ladungen (Beobachtung von Coulomb):
r r
Q1 ⋅ Q2
F (r ) = K ⋅
r2
;
Das Coulomb‘sche Gesetz ist mathematisch äquivalent zum
Gravitationsgesetz.
Alle Aussagen über die Gravitation gelten auch für Ladungen, mit dem
Unterschied, dass Ladungen zwei Vorzeichen haben können.
Die Ladungsmenge (SI Einheit) ist mit C (Coulomb) bezeichnet.
ε0 ist die Dielektrizitätskonstante des Vakuums
Welche WW (Fernwirkungskraft) überwiegt ?
Gravitations- oder elektrostatische WW ?
Die Coulombkraft ist eine Zentralkraft, d.h., sie wirkt in der
Verbindungslinie von zwei Punktladungen Man kann die Ladungen
bewegen - die Kräfte wirken immer entlang der Verbindungslinie.
Elektrostatische Kräfte sind additiv.
Gibt es mehrere Ladungen Q, so ist
die Kraft die alle Ladungen auf eine
Ladung q ausüben die vektorielle
Summe der Kräfte die alle Ladungen
Q auf die Ladung q ausüben.
Kontakt – und Reibungselektrizität (1)
Reibt man einen Glas- oder einen Hartgummistab, findet man 2
verschiedene Arten der Elektrizität:
Der „glaselektrische“ Zustand wird als positiv (+) und der „harzelektrische“
als negativ (-) bezeichnet (Lichtenberg 1778).
Beim Reiben entstehen stets gleichgroße, entgegengesetzte Ladungen. Die
Ladungen werden nicht erzeugt, sondern nur getrennt und in ihrer Wirkung
zum Vorschein gebracht.
Speziell bei den Isolatoren gibt es solche zu denen die
Elektronen eine größere Affinität haben (z.B.
Hartgummi) als zu anderen wie z.B. die Haare eines
Katzenfells.
Bringt man durch Reibung zwei Materialien
unterschiedlicher Elektronenaffinität in innigen
Kontakt, so gehen Elektronen von dem einen Isolator
zum anderen. Bei dem Isolator mit geringerer
Elektronenaffinität bleiben positive Ionen (rosa)
zurück.
Kontakt – und Reibungselektrizität
‡ In der Elektronenhülle der Atome
nehmen die Elektronen unterschiedliche
diskrete Energieniveaus ein. Bei Metallen
an die Stelle des einzelnen Energieniveaus
gibt es ein ganzes Bündel sehr eng beieinander
liegender Energieniveaus.
‡ Bei verschiedenen Stoffen sind die
Energieniveaus unterschiedlich aufgefüllt.
‡ Bei Berührung fließt ein Diffusionsstrom, bis die
Aufladung durch fehlende bzw. überschüssige
Elektronen weiteren Transport verhindert – es
entsteht ein Gleichgewicht der allerdings zum
Elektronenüberschuss, bzw. Mangel an der
Berührungsfläche führt
‡ Diese Effekte treten zwischen allen Materialien
ein – bei Isolatoren bleibt die Trennung erhalten, bei
Leitern ist es schwer verwirklichbar, meistens fließen
die Ladungen über den letzten Berührungspunkt ab.
Elektrisches Feld, Elektrische Feldstärke
Kraftwirkungen von Ladungen sind über große Distanzen beobachtbar – es ist
somit nützlich den Begriff des elektrischen Feldes einzuführen.
In einem Raum wird durch eine elektrische Ladung auf eine andere Ladung eine
Kraft ausgeübt. Dieser Raum wird elektrisches Feld genannt.
Die Stärke und Richtung des elektrischen Feldes wird durch die Feldlinien
dargestellt. Die Ursache des elektrischen Feldes ist die Ladung Q.
Die Wirkung kann z.B. durch eine “Probeladung – q” untersucht werden.
Um das Feld zu beschreiben und von der Probeladung unabhängig zu sein,
kann man die wirkende Kraft auf die Probeladung q beziehen.
Diese neue Größe nennt man die elektrische Feldstärke E:
1 Q
F
⋅ 2
E= ; → E=
4πε 0 r
q
→
⎡N ⎤
⎢⎣ C ⎥⎦
Damit kann in jedem Punkt des Raumes das E-Feld bestimmt werden
Das elektrische Feld kann durch Feldlinien veranschaulicht
werden
E – Feld einer Punktladung
E – Feld von zwei entgegengesetzt
gleich großen Ladungen (rot: +; blau:- )
Positive Ladung nennt man Quelle, die
negative die Senke eines E-Feldes
* Feld einer ruhenden Punktladung
* Feld einer unendlich langen „geladenen Linie“
Leiter im E- Feld:
Die Feldlinien enden stets
NORMAL auf die
Oberfläche, da sich im
Leiter bewegliche
Ladungen befinden
( E –Feld kann in ┴
und║ Komponente zerlegt
werden, die ║
Komponente
„verschwindet“ (warum ?)
und die ┴ bleibt, somit
stehen die Feldlinien
normal auf die
Leiteroberfläche.
Bildladung und „Faradaykäfig“
Feldlinien in der nähe eines Leiters - sie können mit einer Bildladung erklärt
werden.
Da elektrische Feldlinien immer senkrecht auf der Oberfläche eines Leiters
stehen müssen, sieht das Feldlinienbild einer Punktladung in der Nähe eines
Leiters wie die Hälfte des Feldlinienbildes eines Dipols aus. Das elektrische
Feld der Punktladung erzeugt an der Oberfläche die Influenzladung , die das
äussere Feld im Leiter abschirmt → Faradaykäfig.
Leiter haben im inneren keine statischen E-Felder (Feldfreier Raum)
Das E - Feld kann durch Feldlinien experimentell veranschaulicht werden
Wichtige Fakten zusammengefaßt:
Elektrostatisches Potential (Potenzial), Äquipotentialflächen und Spannung
Da eine elektrische Ladung im elektrischen Feld eine Kraft erfährt, wird bei ihrer
Bewegung durch das elektrische Feld Arbeit verrichtet, bzw. es muss Arbeit
verrichtet werden, um die Ladung gegen das elektrische Feld zu bewegen.
Arbeit (dW) = Kraft (F) . Weg (ds) (skalares Produkt)
Die gesamte Arbeit ergibt sich durch Summation, bzw. Integration über die
Einzelarbeiten:
2
→
→
W1→2 = ∑ dW = ∫ F ⋅ d s
1
Die benötigte Arbeit
hängt nur vom Startund Zielort ab, nicht
vom genauen Weg !
1
2
Auf den Kreissegmenten (grün) ist der Wert des Integrals = 0, warum ?
Die Arbeit zur Verschiebung einer Probeladung q im Feld einer Punktladung Q
(Verschiebungsarbeit) ist gegeben durch:
→
W1→2
Q.q
=
4πε 0
⎛1 1⎞
⋅ ⎜⎜ − ⎟⎟
⎝ r1 r2 ⎠
Fall 1: r1 > r2 → W1→2 < 0;
Fall 2: r1 < r2 → W1→2 > 0
Um von der Größe der Probeladung q unabhängig zu sein dividiert man die
Arbeit durch die Probeladung q.
W1→2
= ΔU
q
Es ist die Differenz der potentiellen Energien zwischen
den Punkten 1 und 2 – man nennt es Potentialdifferenz,
oder elektrische Spannung.
Die Einheit ist (Joule/Coulomb) = Volt (V)
Man ordnet einer Ladung im ∞ die potentielle Energie Null, und somit diesem
Punkt auch das Potential Null. Damit ergibt sich für das Potential eines Punktes
im Abstand r von einer Punktladung Q:
∞
W
Q 1
ΔU =
= ∫ E ⋅ q ⋅ ds ⇒ U (r ) = ∫ E ⋅ ds =
⋅
q
4πε 0 r
r
Ist ein Raumpunkt mit einem Potential U bestimmt, kann man Flächen gleicher
Potentiale – die Äquipotentialflächen finden. Eine Ladungsverschiebung über
diese Fläche → keine Veränderung der potentiellen Energie.
Äquipotentialflächen einer Punktladung –
je größer das Potential desto näher liegt
die Äquipotentialfläche der Ladung, desto
höher die Feldstärke.
Die Äquipotentialflächen stehen senkrecht
auf die Feldlinien → eine Leiteroberfläche
muss eine Äquipotentialflächen sein.
Feld und Äquipotentialflächen von 2 Ladungen
Plattenkondensator, Kapazität, Dielektrikum
Ein Plattenkondensator besteht im wesentlichen aus 2 parallelen, sich im Abstand d
voneinander befindlichen leitenden, voneinander isolierten Platten. Werden die Platten
unterschiedlich (+, bzw. -) geladen so entsteht im Inneren des Kondensators ein weitgehend
homogenes elektrisches Feld mit einer konstanten Feldstärke E.
Elektrisches Feld des geladenen
Kondensators, die Inhomogenität
der Randzonen kann durch die
Teilung einer Platte wesentlich
verbessert werden.
Die Spannung zwischen den
Platten ergibt sich aus
d r
r
U = ∫ E ⋅ ds
0
Wir erhalten: U = E . d
Im Außenraum des Plattenkondensators kompensieren sich die Felder der
Ladungsverteilungen der beiden Einzelplatten.
Die Feldstärke (und somit die Spannung) zwischen den Platten hängt von der
Ladung Q ab. Die Spannung und Ladung sind zueinander proportional:
Q = C . U; den Proportionalitätsfaktor C nennt man die Kapazität des Kondensators
Die Kapazität eines Kondensators (ist auch von den Abmessungen abhängig)
gibt die gespeicherte Ladung Q bezogen auf die Potentialdifferenz U an:
Q
C=
U
Die Kapazität C ist von der
Plattenfläche A und vom
Plattenabstand d abhängig.
Es gilt:
A
A
bzw. C = ε 0ε r
C = ε0
d
d
(was ist nun die εr ?)
Relative Dielektrizitätskonstante εr
einiger Stoffe bei 20°C
Gibt es im Kondensator einen Isolator (Dielektrikum)
so werden aufgrund der Spannung die Dipole
ausgerichtet und dadurch die Feldstärke verringert,
dadurch aber die Kapazität erhöht:
C = ε0
A
A
bzw. C = ε 0ε r
d
d
Die relative Dielektrizitätskonstante gibt somit eine
relative Kapazitätszunahme des Kondensators an.
Permanente Dipole ohne / mit Feld
Beim anlegen eines äusseren Feldes an
Isolatoren werden sich im Isolator entweder
Dipole bilden, oder werden ausgerichtet.
Ein Dipol ist „ein neutrales Stück Materie, bei
dem das Zentrum der positiven und negativen
Ladung nicht zusammenfallen“.
Unpolares Medium ohne / mit Feld
Energiespeicherung im Kondensator
Das Aufladen eines Kondensators ist mit Arbeitsaufwand gebunden. Je
höher die Ladung desto größer der Arbeitsaufwand:
q
Arbeit dW ist das Produkt von Ladung dq und
dW = dq ⋅ u
u=
Potentialdifferenz u
C
Die Gesamtenergie ergibt sich aus der Summation (oder Intergration) aller Beiträge dW:
Q
qdq 1 Q 2 1
W=∫
=
= CU 2
C
2 C 2
0
Mit
2
ε
ε
ε
ε
εε
U
A
1
W = CU 2 = 0 r U 2 = 0 r 2 ( Ad ) = 0 r E 2V
2
2 d
2 d
2
C = ε 0ε r
erhält man (mit dem Vol. V=A.d) für die Energiedichte w (unabh. von der
Geometrie des Kondensators):
W
1
= w = ε 0ε r E 2
V
2
Die Energie eines geladenen Kondensators steckt im elektrischen Feld.
A
d
Kondensator – Etwas Geschichte.
Die Leidener Flasche ist die älteste Bauform eines Kondensators. Sie
besteht aus einem Glasgefäß, an dem Metallbeläge auf der Innen- und
Außenseite angebracht sind. Das Glas wirkt hierbei als Isolator.
Das Prinzip der Leidener Flasche wurde 1745 von dem Physiker Pieter
van Musschenbroek in Leyden gefunden, als er bei Laborversuchen mit
entsprechenden Anordnungen von Gläsern und Metallteilen elektrische
Stromschläge erhielt.
ca. 200 Jahre
„Elektrostatischer“ Kuss
Schaltung und Anwendung von Kondensatoren
Kondensatoren sind unumgängliche Bestandteile von allen Geräten
und Instrumenten die auf der Basis der Elektrizität arbeiten. Sie finden
vielfache Anwendungen in vielen Bereichen, wie Elektronik,
Elektrotechnik, Radiotechnik, Messtechnik, Haustechnik, ….
Die entsprechende Wahl der Größe (Kapazität) von Kondensatoren
kann durch eine entsprechende Kombination von diesen
elektronischen Bauteilen erreicht werden:
→ PARALLELSCHALTUNG
→ SERIENSCHALTUNG (auch REIHENSCHALTUNG genannt)
PARALLELSCHALTUNG –
alle Kondensatoren liegen auf der gleichen Spannung
+
Qi = U ⋅ Ci
U
-
C ges = ∑ Ci
i
SERIENSCHALTUNG –
alle Kondensatoren haben die gleiche Ladung Q
Ui =
Q
Ci
; U = ∑U i
i
1
1
=∑
CGes
i Ci
Elektrisches Feld der Erde
Schematische Ladungsverteilung
an der Erdoberfläche in der
unteren Atmosphäre und E-Feld
der Erde als Funktion der Höhe
Auf einer leitenden Kugel verteilen
sich Ladungen immer so, dass die
Kugeloberfläche eine
Äquipotezialfläche wird.
Leitende Kugel hat eine gleichmäßige
Oberflächen Ladung. Im Außenraum
erzeugt sie das gleiche Potenzial wie
eine im Zentrum vereinigte Ladung
Potential einer (Punkt) Ladung:
Q
1
U=
⋅ und
4πε 0 r
Q
C=
U
Die Kapazität einer Kugel mit dem
Radius R:
E(Erde) = 130 V /m
Q(Erde) = - 6.105 C
In der Atmosphäre gibt es Ladungsträger beider
Polaritäten. Untere Schichten : Überschuß an
pos. Ionen – Abschirmung von E(Erde) und
Abnahme mit der Höhe
C = 4πε 0 ⋅ RE
Kapazität der Erde
CE = 0.7 mF
Elektrostatische
Staubfilter
Staubemissionskontrolle
von Industrieanlagen und
Kraftwerken
Hochspannung
Zusammenfassung
Elektrostatik (Erscheinungen die von ruhenden Ladungen stammen):
¼ Ladungen – Arten (+;-), Wechselwirkung (Kraft)
E=
¼ Elektrisches Feld, Elektrische Feldstärke
¼ Elektrostatisches Potential, Spannung
r r
Q ⋅Q
F (r ) = K ⋅ 1 2 2
r
[N ]
F
1 Q
⋅
; → E=
q
4πε 0 r 2
⎡N ⎤
⎢⎣ C ⎥⎦
∞
W
Q 1
ΔU (r ) = ⇒ ∫ E ⋅ ds =
⋅ [V ]
4πε 0 r
q
r
A Q
C = ε 0ε r =
d U
¼ Plattenkondensator, Kapazität, Dielektrikum
¼ Schaltung und Anwendung von Kondensatoren
C ges = ∑ Ci
i
1
1
=∑
CGes
i Ci
[F ]
GLEICHSTROM –
die gleichmäßige, zeitlich konstante Bewegung von elektrischen Ladungen
(Ladungsträger: Elektronen, positive und negative Ionen)
• der schwächste Gleichstrom transportiert in sehr kurzen Zeiten viel mehr Ladung
als man durch Reibung erzeugen konnte
• in Elektrostatik (ruhende Ladungen) – keine Potentialdifferenz längs eines Leiters
• im täglichen Leben legt man stets Spannungen an Leitern → Ladungsbewegung
(Strom)
I=
dQ
dt
⎡C ⎤
⎢⎣ s ⎥⎦ ≡ [A]
Wenn in 1s durch einen Leiter eine Ladung von 1C (etwa 6.1018 e) fließt →
Stromstärke von 1 Ampere
• Die Ströme können nur auf Kosten äußerer Energiequellen aufrechterhalten
werden, sonst würde sehr schnell der von der Elektrostatik geforderte Zustand
eintreten
• Spanungsquellen – Batterien, Netzgeräte, Netz
• Stromrichtung – aus historischen Gründen wird die Richtung definiert als die
Flußrichtung positiver Ladungsträger, auch wen sich später zeigte, dass in
Metallen der Strom von negativen Ladungsträger, den Elektronen, verursacht wird.
Die technische Stromrichtung ist also immer von PLUS nach MINUS.
+
-
Der elektrische Widerstand und das Ohm‘sche Gesetz
Bei vielen Leitern beobachtet man eine
Proportionalität zwischen I(A) und U(V) – der
Proportionalitätsfaktor R heißt der (elektrische)
Widerstand: U = R . I; R=U/I
⎡ Volt ⎤
[R] = ⎢
= Ω (Ohm)
⎥
⎣ Ampere ⎦
Beim homogenen Leiter ist der Widerstand
proportional zur Länge l und umgekehrt
proportional zum Querschnitt des Leiters:
U
l
R= = ρ⋅
I
A
[Ω]
ρ heißt spezifischer Widerstand des Materials.
Manchmal wird auch der Kehrwert σ = 1 / ρ (spez.
Leitfähigkeit) verwendet.
Spezifische Widerstände
einiger Leiter und
Isolatoren (bei 20°C)
GLEICHSTROMNETZWERKE
Leicht
Leicht
Auch leicht, aber wie
gehen wir hier vor ?
• Gleichstromnetzwerke – Kirchhoff‘schen Regeln
Wie viele Maschen
haben wir hier ?
Reihenschaltung von Widerständen
U ges = U1 + U 2 + U 3 + U 4
U ges = I ( R1 + R2 + R3 + R4 )
U ges = I ⋅ Rges
Der Gesamtwiderstand Rges einer Reihenschaltung errechnet
sich indem man die Einzelwiderstände addiert.
Rges = R1 + R2 + ... + Rn
Da es sich bei der Reihenschaltung um einen unverzweigten
Stromkreis handelt fließt überall der gleiche Strom.
Die Stromstärke I ist also überall in der Schaltung gleich groß.
An jedem Widerstand liegt eine elektrische Spannung an. Diese
ist umso größer, je größer der jeweilige Widerstand ist.
Rges = ∑ Ri
i
Parallelschaltung von Widerständen
U
An allen
Widerständen liegt
hier die gleiche
Spannung U
I = I1 + I 2 + I 3
U
U U U
1
1
1
= +
+
=U( +
+ )
Rges R1 R2 R3
R1 R2 R3
1
1
= ∑ = Gges
Rges
i Ri
⎡1⎤
⎢⎣ Ω ⎥⎦ ≡ [1S ] ( Siemens)
Die Leistung und Arbeit des elektrischen Stromes
Werden unter dem Einfluss der elektrischen Spannung U
Ladungsträger mit der Elektrizitätsmenge Q bewegt, so wird dabei
eine Arbeit W verrichtet.
Es handelt sich dabei um die elektrische Arbeit, gegeben durch:
W=QxU
Elektrizitätsmenge: Q = I × t
Die Elektrizitätsmenge Q besteht aus dem elektrischen Strom I und
der Zeit in Sekunden in der dieser Strom fließt. Somit erhalten wir:
W=UxIxt
(Joulsches Gesetz)
Elektrische Arbeit = Spannung × Strom × Zeit
W = P x t in (Ws ) = (V x A x s)
Elektrische Arbeit = Leistung x Zeit
Aus der Spannung U und der Strom I die Leistung P berechnet.
Für Leiter für die das Ohmsche Gesetz gilt, kann man auch schreiben:
2
U
P =U ⋅I = I2 ⋅R =
R
Stromleitung in Flüssigkeiten
• Reines Wasser ist kein guter Stromleiter
• Man kann eine Lösung durch Zusatz von z.B. Salz leitend machen
• Verdünnte Salzlösungen, Säuren und Basen sind gute Stromleiter
• Durch Auflösen eines Salzes in Flüssigkeit entsteht eine leitende
Lösung – der Elektrolyt
• Die Aufteilung des gelösten Stoffen in positive und negative Ionen:
Dissoziation
.
Ladungstransport in Flüssigkeiten
Kathode
Anode
Destilliertes Wasser:
Kein Strom, da Ladungsträger
fehlen
H2O
HCL
Salzsäure (HCL) : Dissoziation!
es sind positiv geladene H+ – Ionen und
negativ geladene Cl- – Ionen vorhanden:
Strom kann fließen!
Dissoziation: Ionentrennung durch
Analgern von Wassermolekülen
Salzsäure: H CL
Zusammenstellung einiger Fakten:
• Elektrolyte sind somit leitende Flüssigkeiten
• Man teilt sie in Säuren, Salze und Basen. Elektrolyte werden beim Auflösen
in Wasser durch Dissoziation in Ionen aufgespaltet.
• Die Stromleitung in Elektrolyten erfolgt somit durch frei bewegliche Ionen.
• Beim Anlegen einer Spannung wandern sie positiven Ionen zum negativen
Pol (Kathode), die negativen Ionen zum positiven Pol (Anode).
• Weil die Ionen größer als Elektronen sind ist der spez. Widerstand von
Elektrolyten wesentlich größer (typ. Faktor 100) als von Metallen
• Gleichzeitig mit der Ladung transportieren die Ionen auch eine Masse. Es
kommt daher auch zu einem Massentransport, ein wesentliches
Kennzeichen der elektrolytischen Stromleitung.
Technische Anwendungen der Elektrolyse sind z. B. die Gewinnung reiner
Stoffe oder die Herstellung von Batterien.
Einschub (über die Basiseinheit Stoffmenge):
Als Molekulargewicht - genauer: Molekularmasse oder Molekülmasse bezeichnet man die Summe der Atommassen aller Atome in einem
Molekül.
Zur Bestimmung der Molekularmasse eines x-beliebigen Moleküls addiert
man einfach die Atommassen aller am Aufbau des Moleküls beteiligten
Atome.
Beispiele:
Formel: H2O Molekularmasse 2 × 1 + 16 = 18
Formel: CO2 Molekularmasse 12 + 2 × 16 = 44
Das Mol ist die SI-Basiseinheit der Stoffmenge. Es wird definiert als
diejenige Menge einer Substanz, die so viele Teilchen (Atome, Moleküle,
Ionen oder Elektronen) enthält, wie Atome in 12 Gramm des KohlenstoffIsotops 12C enthalten sind.
Die Teilchenzahl pro Mol (Avogadrokonstante NA, Loschmidtzahl (L)) beträgt:
L= NA = 6,0221367 × 1023 Mol-1 = 6,0221367 x 1026 kMol-1
Beispiel:
Lösung von NaCl in Wasser: 0,2 kMol / m3, Elektrodenfläche A: 0,01m2,
Stomstärke I: 1 A.
Anzahl der Ionen (+ und -) nach vollständiger Dissoziation:
n- =0,2 . 6,.1026 = 1,2.1026 Ionen, ebensoviele n+.
Driftgeschwindigkeit v = I/n.A.e = 1 / (2,4.1026).(0.01).(1.6.10-19) = 2.6 μm/s
Gleichzeitig mit der Ladung transportieren die Ionen auch eine Masse
Um 1 kMol einer Substanz an einer Elektrode abzuscheiden benötigt man
eine Ladungsmenge
Q = z.e.L
e… Elementarladung, z…Ladungszahl, L…Loschmidtzahl (Avogardozahl)
kF = e.L = 0,965 . 108 As/kMol (Faraday-Konstante)
Faraday forschte viel auf dem Gebiet der Stromleitung in Flüssigkeiten. Dabei hat
er auch eine Methode zur Freisetzung von Metallen entwickelt. Diese Methode
nannte Faraday Elektrolyse (nach einem griechischen Ausdruck für „mittels
Elektrizität befreien“).
Das FARADAY'sche Gesetz besagt, dass die in einem Elektrolyten die
transportierte Masse der transportierten Ladung proportional ist:
m Transportierte Masse [kg]
M Molmasse [kg/kMol]
Q Transportierte Ladung [As]
z Ladungszahl pro Molekül, z.B. 1 für Na+; -2 für SO4 -kF Faradaykonstante = 0,965.108 As/kMol
M ⋅Q M ⋅ I ⋅t
m=
=
z ⋅ kF
z ⋅ kF
Wie lange muß ein Strom
von 10A fließen um 1 kg Cu
aus einer CuSO4 Lösung
abzuscheiden ?
1kg ⋅ 2 ⋅ k F
5
t=
= 3,04 ⋅10 s ≈ 3,5 Tage
63,5 ⋅10 A
Stromleitung in Gasen und Vakuum
Die Stromleitung in Gasen stellt ein kompliziertes Phänomen dar, denn
freie Ladungsträger können auf vielfache Weise erzeugt werden. Und
die Ladungsträger können sowohl Elektronen (q = -e) wie auch
positiv oder negativ geladene Ionen sein.
Man bezeichnet das Auftreten eines elektrischen Stroms in einem Gas
als Entladung.
Prinzipiell werden unterschieden:
Unselbständige Entladung
Es werden die freien Ladungsträger
durch äußere Einflüsse erzeugt.
Selbständige Entladung
Es werden die freien Ladungsträger
durch das elektrische Feld selbst erzeugt.
Unselbständige Entladung
Quellen für die Erzeugung freier Ladungen sind:
- Hohe Temperatur
- erhitzte Metalloberflächen
- heiße Flamme
Teilchenstrahlung
- radioaktive Quellen (natürliche oder künstliche)
- kosmische Höhenstrahlung
Elektromagnetische Strahlung (bestimmte Wellenlängen)
In allen Fällen werden die Gasatome ionisiert (d.h. in ein Elektron und
ein positives Ion zerlegt), oder dissoziiert (d.h. in zwei gegensätzlich
geladene Ionen zerlegt).
Strom – Spannung – Charakteristik
eines ionisierten Gases
• Gefäß mit 2 Elektroden – A und K
• Niedriger Gasdruck (einige hundert Pa)
• Erzeugung von Ladungsträger (z.B.γ)
• Messung von Strom als Funktion der
Spannung
• U prop. zu I
• Sättigungsbereich – I steigt nicht an
• Oberhalb von Uc – Stoßionisation (abh.
von p, Gasart)
• Oberhalb von UZ – selbständige
Entladung bleibt erhalten auch ohne
von außen erzeugte Ladungen
Supraleitung
Widerstandsfreie - also verlustfreie (R¼0) - Leitung elektrischen Stroms, welche
unterhalb einer bestimmten Temperatur (Sprungtemperatur) einsetzt.
Diese Temperatur ist eine Materialkonstante.
Kamerlingh Onnes hatte beobachtet, dass Quecksilber bei Abkühlung auf
Temperaturen unterhalb von 4 Kelvin (Sprungtemperatur), also bei ungefähr -270 °C
den elektrischen Strom völlig verlustlos und ohne sich dabei zu erwärmen leitet.
(Nobelpreis 1913 !!!)
Ideal zum Transport der elektrischer Energie
Die widerstandsfreie elektrische Leitung ist gleichbedeutend mit der Tatsache, dass beliebige
Distanzen verlustfrei überwunden werden können.
Damit wäre ein weltweites Verbundnetz realisierbar: Solarstrom würde in den sonnenreichen
Gegenden der Erde erzeugt, genutzt werden kann der Strom dann auch in den sonnenärmeren
Gebieten. In einem geschickten weltweiten Verbund könnte Solarenergie ohne Speicher benutzt
werden, wenn rund um die Erde und damit rund um die Uhr Strom erzeugt und auf der ganzen
Erde verteilt werden könnte.
Der Bau supraleitender Fernleitungen scheitert jedoch u.a. an der Notwendigkeit einer Kühlung
der Leitung.
Bis jetzt: einige Nobelpreise – Wunschtraum: Supraleitung bei Raumtemperatur
Elektrizität in Biosystemen
• Zelle - die kleinste lebensfähige Einheit des Tier- u. Pflanzenreiches
• Zelle ist umgeben von der Zellmembran – sie ist selektiv durchlässig . Durch die
Zellmembran steht die Zelle mit der äußeren Umgebung in Verbindung.
Die Proteine auf der Zellmembran erleichtern diese Wechselwirkung.
• Funktion und Eigenschaft
- Aufbau elektrischer Potenziale
- Zellmembran ist semipermeabel
- Passt sich der Formveränderung
der Zelle an
- Erregungsweiterleitung
Über die Membran
besteht eine
Potentialdifferenz
Sie besteht vorwiegend aus Lipiden
und Proteinen, Dicke – 7 bis 9 nm.
Die Zahl der positiven und negativen Ladungen ist in beiden Würfeln (links und
rechts von der Membran) gleich, d.h. beide Räume sind elektrisch neutral.
Die jeweiligen Ionensorten sind aber unterschiedlich verteilt: Im Zellplasma
dominieren K+ - Ionen und Proteinat-Ionen, in der Interzellularflüssigkeit
herrschen Na+ Ionen vor.
Bezüglich der Na+ - und K+ - Ionen herrscht also Ungleichverteilen, ebenso
zwischen den Chlorid-Ionen im Zellinnern und im Außenraum.
Proteinat-Ionen finden sich nur im Plasma der Nervenzelle.
Innenseite der Membran
100 000 K+
A
-
10 000 Na+
107 800 Proteinat-Anionen A 2 200 Chlorid-Ionen
Cl -
Außenseite der Membran
2 000 K+
Membran
Membran
108 000 Na+
110 000 Cl -
Gleichgewichtspotentialdifferenz
RT ⎛ ci ⎞
U=
⋅ ln⎜⎜ ⎟⎟
kF
⎝ ca ⎠
Zur Erklärung des Membranpotentials U:
Um das Zustandekommen des Membranpotentials zu verstehen, müssen wir zwei
Gradienten für jeweils eine Ionensorte
(K+ oder Na+ ) betrachten:
Die K+ Diffusion
a) Chemischer Gradient (Diffusionsgradient) für K+ ist
von innen nach außen gerichtet Ö K+ : Ausstrom aus dem
Zellinnern
b)
Elektrischer Gradient für K+ ist dem chemischen
Gradienten entgegengesetzt Ö K+ : Einstrom.
Ungleichverteilung der
Gesamtionen
Was wäre die Folge, wenn nur diese Gradienten den K±
Strom über dem Membran in Ruhe kontrollieren würden?
Es käme zu einem Ausstrom von K+ Ionen so lange, bis
sich ein Gleichgewicht zwischen dem nach außen
diffundierenden K+ und dem diesem Diffusionsbestreben
entgegengesetzen elektrischen Gradienten ausgebildet hat.
Das Ergebnis wäre ein konstantes K+ Gleichgewichtspotential von etwa - 90 mV.
Da auch Na+ und Cl- Ionen vorhanden sind Ö Ruhepotential (RP) von etwa -70 mV
Nervenimpulse (Abweichung der Spannung über d. Membran vom RP)
Nervenzellen → Aufnahme, Verarbeitung und Weiterleitung von Reizen
(Signalen, Informationen). Sie kommen nur bei Tieren und Menschen vor. Obwohl
auch Pflanzen, Pilze reizbar sind besitzen sie keine Nervenzellen.
Informationsaufnahme
Verarbeitung
Stört man das empfindliche Gleichgewicht (RP) dann
reagiert die Zellmembran sehr heftig Ö so öffnen sich
an der Stelle des Reizes plötzlich Poren in der
Zellmembran (Natriumkanäle), wodurch es zu einem
Ladungsausgleich zwischen dem positiven Außen- und
dem negativen Innenraum kommt (Depolarisation)
Leitung
Im Gegensatz zum Ruhepotential nennt man diese
Reaktion Aktionspotential.
Informationsübertragung
Nach dem Reiz schon bald bildet sich das RP zurück, indem sich zunächst
Kaliumkanäle öffnen, die positive Kalium-Ionen aus der Zelle ausströmen lassen,
und indem sich die Natriumkanäle von selbst wieder schließen und somit der
Na+ -Einstrom gebremst wird (Natrium-Kalium-Pumpe).
Das Ruhepotential (RP) einer
Nervenzelle ist das elektrische
Potential, die Spannung also, die
man dann messen kann, wenn sich
die Zelle im elektrochemischen
Gleichgewicht befindet.
Experimentelle Aufnahme d. Aktionpotentials
Das Aktionspotential (grün) zeigt einen
typischen typischen Verlauf, den man in
7 Phasen einteilen kann.
1. Ruhepotential
2. Depolarisierung
3. Positive Rückkopplung
4. Peak
5. Repolarisierung
6. Hyperpolarisierung
7. Wiederherstellung des Ruhepotentials
A. KONTINUIERLICHE ERREGUNGSLEITUNG (Axon)
Grenzt erregter Bereich an einen unerregten Bereich → innen als auch außen an
der Membran gibt es benachbarte,entgegengesetzt geladene Zonen →
Ionenwanderung - zunächst innen und außen der Membran entlang, dann auch
durch diese hindurch.
Die Membran wird so stark depolarisiert, dass ein neues Aktionspotential ausgelöst
wird. Ein neuer Grenzbereich bildet sich, wiederum wandern Ionen, die
Membran wird depolarisiert, neue Aktionspotentiale werden ausgelöst.
Fortschreitende Depolarisation führt also zum kontinuierlichen Fortschreiten
von Aktionspotentialen über das Axon.
Zahlreiche Pharmaka und Drogen wirken an den Synapsen, indem sie die Impulsübertragung
beschleunigen oder verlangsamen. Wobei es verschiedene Transmitter und Rezeptoren gibt.
Muscarin (Gift des Fliegenpilzes) lagert sich als Muscarischer- Acetycholin- Rezeptor an. Das
Gift der Tollkirsche (auch Belladonna und Atropin) wirkt über denselben Rezeptor.
Opium, Morphium, Heroin wirken über die sogenannten Opiat- Rezeptoren.
(B) SALTATORISCHE ERREGUNGSLEITUNG:
Laufen Aktionspotentiale über bestimmte Axone, die Zellen mit dichter
Isolationshülle bilden, können nur an den Schnürringen (Ranviersche Schnürringe)
Aktionspotentiale entstehen. Die Strecke dazwischen, je nach Axon (1 - 5 mm),
wird von den Ionen „überbrückt", die zum Ladungsausgleich innen an der
Axonmembran und außen an den Schwannschen Zellen entlangwandern.
Die Aktionspotentiale laufen also nicht kontinuierlich über das Axon, sondern
springen von Schnürring zu Schnürring. Diese Art der Erregungsleitung geht
rascher: Diese Axone leiten bei einem Durchmesser von 10-20 µm die Erregung
mit Geschw. bis 130 m/s.
Einige Zahlenbeispiele:
Kapazität (Zellenmembran) beträgt etwa 0.01 F/m2 (!!)
Ein Plattenkondensator von 1 m2 und d=9nm → 0.001F
daraus folgt, dass Membran ein Dielektrikum sein muss
mit ε = 10. Auch die Feldstärke über d. Membran ist
gigantisch: E=U/d → 70mV / 7nm = 10 Megavolt / m (!)
Die Oberfläche aller Zellen beträgt etwa 21000m2.
C = ε 0ε r
A
d
Q
qdq 1 Q 2 1
W=∫
=
= CU 2
C
2 C 2
0
P=
W
t
Die Gesamtkapazität ergibt sich zu C(ges) = 210 F (!!!!)
Die gespeicherte Energie W (ges)=0.5CU2 = 0.52 Joule
Ann.
Es dauert etwa 10 ms bis eine Zelle wieder bereit ist Reize zu verarbeiten →
Ka-Na-Pumpe muss eine Arbeit verrichten (ATP – adenosine triphosphate).
Die erbrachte Leistung P:
P=0.52 J / 0.01 s = 52 W.
In 24 Stunden ergibt es die Energiemenge von 4493 kJoule
Tägliche Nahrungsaufnahme: etwa 10000kJ, also ca. 50% der Energie könnte
für die Impulsverarbeitung verwendet werden.
Eine kleine
„Gedächtnisstütze“
U
R=
I