3. Juni 2015

Datenstrukturen und Algorithmen
Graphalgorithmen
Darstellung von Graphen
Java
public void addNode(V u) {
nodes.add(u);
edges.put(u, new LinkedListhVi());
}
Java
public void addEdge(V s, V t) {
ListhVi adjlist = edges.get(s);
adjlist.add(t);
if(!directed) {
adjlist = edges.get(t);
adjlist.add(s);
}
}
(Folie 185, Seite 58 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Darstellung von Graphen
Java
public void delEdge(V s, V t) {
ListhVi adjlist = edges.get(s);
adjlist.remove(t);
if(!directed) {
adjlist = edges.get(t);
adjlist.remove(s);
}
}
(Folie 186, Seite 58 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
Übersicht
3
Graphalgorithmen
Darstellung von Graphen
Tiefensuche
Starke Komponenten
Topologisches Sortieren
Kürzeste Pfade
Netzwerkalgorithmen
Minimale Spannbäume
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 187, Seite 58 im Skript)
Tiefensuche
Tiefensuche ist ein sehr mächtiges Verfahren, das iterativ alle
Knoten eines gerichteten oder ungerichteten Graphen besucht.
Sie startet bei einem gegebenen Knoten und färbt die Knoten
mit den Farben weiß, grau und schwarz.
Sie berechnet einen gerichteten Tiefensuchwald, der bei einem
ungerichteten Graph ein Baum ist.
Sie ordnet jedem Knoten eine Anfangs- und eine Endzeit zu.
Alle Zeiten sind verschieden.
Die Kanten des Graphen werden als Baum-, Vorwärts-,
Rückwärts- oder Querkanten klassifiziert.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
1/
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
1/2
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
3/
1/2
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/
3/
1/2
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/
5/
3/
1/2
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/
5/
3/
1/2
6/
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/
5/
3/
1/2
6/7
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/
5/8
3/
1/2
6/7
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/9
5/8
3/
1/2
6/7
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/9
5/8
3/10
1/2
6/7
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/9
5/8
3/10
1/2
6/7
11/
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 188, Seite 58 im Skript)
Tiefensuche – Beispiel
4/9
5/8
3/10
1/2
6/7
11/12
Die Kanten des Tiefensuchwaldes sind dick dargestellt.
Ein Knoten ist anfangs weiß.
Ein Knoten ist grau, während er aktiv ist.
Danach wird er schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
Noch ein Beispiel
(Folie 189, Seite 58 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 190, Seite 58 im Skript)
Java
public void DFS(MaphV, Integeri d,
MaphV, Integeri f, MaphV, Vi p) {
MaphV, Integeri color = new HashMaphV, Integeri();
for(V u : allNodes())
color.put(u, WHITE);
int time = 0;
for(V u : allNodes())
if(color.get(u) == WHITE)
time = DFS(u, time, color, d, f, p);
}
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 191, Seite 58 im Skript)
Java
public int DFS(V u, int t, MaphV, Integeri c,
MaphV, Integeri d, MaphV, Integeri f, MaphV, Vi p) {
d.put(u, ++t);
c.put(u, GRAY);
for(V v : neighbors(u))
if(c.get(v) == WHITE) {
p.put(v, u);
t = DFS(v, t, c, d, f, p);
}
f.put(u, ++t);
c.put(u, BLACK);
return t;
}
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 192, Seite 58 im Skript)
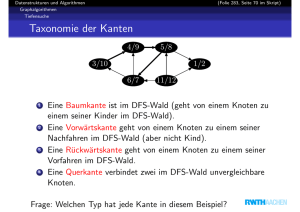
Taxonomie der Kanten
4/9
5/8
3/10
1/2
6/7
1
2
3
4
11/12
Eine Baumkante ist im DFS-Wald (geht von einem Knoten zu
einem seiner Kinder im DFS-Wald).
Eine Vorwärtskante geht von einem Knoten zu einem seiner
Nachfahren im DFS-Wald (aber nicht Kind).
Eine Rückwärtskante geht von einem Knoten zu einem seiner
Vorfahren im DFS-Wald.
Eine Querkante verbindet zwei im DFS-Wald unvergleichbare
Knoten.
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 192, Seite 58 im Skript)
Taxonomie der Kanten
4/9
5/8
3/10
1/2
6/7
1
2
3
4
11/12
Eine Baumkante ist im DFS-Wald (geht von einem Knoten zu
einem seiner Kinder im DFS-Wald).
Eine Vorwärtskante geht von einem Knoten zu einem seiner
Nachfahren im DFS-Wald (aber nicht Kind).
Eine Rückwärtskante geht von einem Knoten zu einem seiner
Vorfahren im DFS-Wald.
Eine Querkante verbindet zwei im DFS-Wald unvergleichbare
Knoten.
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
2/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
2/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
2/
4/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
5/
2/
4/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
5/6
2/
4/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
5/6
2/
4/7
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
1/
5/6
2/
4/7
8/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
5/6
4/7
1/
9/
2/
8/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/
5/6
4/7
1/
9/
2/
8/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
5/6
4/7
1/
9/
2/
8/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
5/6
4/7
1/
9/12
2/
8/
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
5/6
4/7
1/
9/12
2/
8/13
3/
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
5/6
4/7
1/
9/12
2/
8/13
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
15/
1/
9/12
5/6
2/
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
15/16
1/
9/12
5/6
2/
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
15/16
1/
9/12
5/6
2/17
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
10/11
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
19/
10/11
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 193, Seite 58 im Skript)
Taxonomie der Kanten
19/20
10/11
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
Frage: Welchen Typ hat jede Kante in diesem Beispiel?
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
1/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
1/
2/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
1/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
1/
4/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
5/
1/
4/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/
5/
1/
4/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/
1/
4/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/8
1/
4/
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/8
1/
4/9
2/
3/
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/8
1/
4/9
2/
3/10
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/8
1/
4/9
2/11
3/10
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 194, Seite 58 im Skript)
DFS – Ungerichtete Graphen
6/7
5/8
1/12
4/9
2/11
3/10
Wir erhalten immer einen Baum, wenn der Graph
zusammenhängend ist.
Implementierung: Eine ungerichtete Kante wird durch Kanten in
beide Richtungen dargestellt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 195, Seite 58 im Skript)
Taxonomie der Kanten
19/20
10/11
Betrachte Kante (u, v ):
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
1
d(u) < d(v ) und
f (v ) < f (u) ⇐⇒
Baum- oder
Vorwärtskante
2
d(v ) < d(u) und
f (u) < f (v ) ⇐⇒
Rückwärtskante
3
sonst Querkante
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 195, Seite 58 im Skript)
Taxonomie der Kanten
19/20
10/11
Betrachte Kante (u, v ):
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
1
d(u) < d(v ) und
f (v ) < f (u) ⇐⇒
Baum- oder
Vorwärtskante
2
d(v ) < d(u) und
f (u) < f (v ) ⇐⇒
Rückwärtskante
3
sonst Querkante
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 195, Seite 58 im Skript)
Taxonomie der Kanten
19/20
10/11
Betrachte Kante (u, v ):
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
1
d(u) < d(v ) und
f (v ) < f (u) ⇐⇒
Baum- oder
Vorwärtskante
2
d(v ) < d(u) und
f (u) < f (v ) ⇐⇒
Rückwärtskante
3
sonst Querkante
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 196, Seite 58 im Skript)
Tiefensuche
Theorem
Gegeben sei ein gerichteter Graph G = (V , E ) (in
Adjazenzlistendarstellung).
Durch Tiefensuche kann ein DFS-Wald inklusive der Funktionen
d : V → N, f : V → N in O(|V | + |E |) Schritten (also in linearer
Zeit) berechnet werden.
Beweis.
(Skizze) Solange ein Knoten grau ist, wird jede inzidente Kante
einmal besucht. Jeder Knoten wechselt seine Farbe nur zweimal,
jedesmal mit konstantem Aufwand.
Jede Kante wird daher ebenfalls nur einmal besucht.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 197, Seite 58 im Skript)
Zusammenhangskomponenten
Definition
Es sei G = (V , E ) ein ungerichteter Graph. Ein Pfad der Länge k
von u1 nach uk+1 ist eine Folge (u1 , u2 ), (u2 , u3 ), . . . , (uk , uk+1 )
von Kanten aus E wobei u1 , . . . , uk+1 paarweise verschieden sind.
Wir sagen u und v sind zusammenhängend, wenn es einen Pfad
von u nach v gibt.
Eine Menge C ⊆ V ist eine Zusammenhangskomponente, wenn
alle Knoten in C zusammenhängend sind und es keine echte
Obermenge von C mit dieser Eigenschaft gibt.
(Alternativ: Die Zusammenhangskomponenten sind die
Äquivalenzklassen der Relation zusammenhängend“.)
”
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 197, Seite 58 im Skript)
Zusammenhangskomponenten
Definition
Es sei G = (V , E ) ein ungerichteter Graph. Ein Pfad der Länge k
von u1 nach uk+1 ist eine Folge (u1 , u2 ), (u2 , u3 ), . . . , (uk , uk+1 )
von Kanten aus E wobei u1 , . . . , uk+1 paarweise verschieden sind.
Wir sagen u und v sind zusammenhängend, wenn es einen Pfad
von u nach v gibt.
Eine Menge C ⊆ V ist eine Zusammenhangskomponente, wenn
alle Knoten in C zusammenhängend sind und es keine echte
Obermenge von C mit dieser Eigenschaft gibt.
(Alternativ: Die Zusammenhangskomponenten sind die
Äquivalenzklassen der Relation zusammenhängend“.)
”
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 197, Seite 58 im Skript)
Zusammenhangskomponenten
Definition
Es sei G = (V , E ) ein ungerichteter Graph. Ein Pfad der Länge k
von u1 nach uk+1 ist eine Folge (u1 , u2 ), (u2 , u3 ), . . . , (uk , uk+1 )
von Kanten aus E wobei u1 , . . . , uk+1 paarweise verschieden sind.
Wir sagen u und v sind zusammenhängend, wenn es einen Pfad
von u nach v gibt.
Eine Menge C ⊆ V ist eine Zusammenhangskomponente, wenn
alle Knoten in C zusammenhängend sind und es keine echte
Obermenge von C mit dieser Eigenschaft gibt.
(Alternativ: Die Zusammenhangskomponenten sind die
Äquivalenzklassen der Relation zusammenhängend“.)
”
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
1/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
1/
2/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
1/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
1/
4/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
5/
1/
4/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/
5/
1/
4/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/
1/
4/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/8
1/
4/
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/8
1/
4/9
2/
3/
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/8
1/
4/9
2/
3/10
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/8
1/
4/9
2/11
3/10
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 198, Seite 58 im Skript)
Zusammenhangskomponenten
Theorem
Die Zusammenhangskomponenten eines ungerichteten Graphen
können in linearer Zeit gefunden werden.
Beweis.
Die Knoten, die jeweils in einem Aufruf der Tiefensuche schwarz
werden, gehören zu einer Komponente.
6/7
5/8
1/12
4/9
2/11
3/10
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 199, Seite 58 im Skript)
Finden von Kreisen
Theorem
Gegeben sei ein gerichteter Graph G . Dann können wir in linearer
Zeit feststellen, ob G azyklisch ist (keine Kreise enthält).
Beweis.
Führe eine Tiefensuche auf G aus.
Behauptung: G ist genau dann azyklisch, wenn es keine
Rückwärtskanten gibt.
⇒ Wenn es eine Rückwärtskante von u nach v gibt, dann gibt es
auch einen Pfad von v nach u im DFS-Wald. Dies ist ein Kreis.
⇐ Angenommen es gibt einen Kreis. Sei u der Knoten auf dem
Kreis mit minimalem d(u) und v der Knoten auf dem Kreis vor u.
Dann gilt d(u) < d(v ) und f (v ) < d(u).
Also ist (v , u) eine Rückwärtskante.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 199, Seite 58 im Skript)
Finden von Kreisen
Theorem
Gegeben sei ein gerichteter Graph G . Dann können wir in linearer
Zeit feststellen, ob G azyklisch ist (keine Kreise enthält).
Beweis.
Führe eine Tiefensuche auf G aus.
Behauptung: G ist genau dann azyklisch, wenn es keine
Rückwärtskanten gibt.
⇒ Wenn es eine Rückwärtskante von u nach v gibt, dann gibt es
auch einen Pfad von v nach u im DFS-Wald. Dies ist ein Kreis.
⇐ Angenommen es gibt einen Kreis. Sei u der Knoten auf dem
Kreis mit minimalem d(u) und v der Knoten auf dem Kreis vor u.
Dann gilt d(u) < d(v ) und f (v ) < d(u).
Also ist (v , u) eine Rückwärtskante.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 199, Seite 58 im Skript)
Finden von Kreisen
Theorem
Gegeben sei ein gerichteter Graph G . Dann können wir in linearer
Zeit feststellen, ob G azyklisch ist (keine Kreise enthält).
Beweis.
Führe eine Tiefensuche auf G aus.
Behauptung: G ist genau dann azyklisch, wenn es keine
Rückwärtskanten gibt.
⇒ Wenn es eine Rückwärtskante von u nach v gibt, dann gibt es
auch einen Pfad von v nach u im DFS-Wald. Dies ist ein Kreis.
⇐ Angenommen es gibt einen Kreis. Sei u der Knoten auf dem
Kreis mit minimalem d(u) und v der Knoten auf dem Kreis vor u.
Dann gilt d(u) < d(v ) und f (v ) < d(u).
Also ist (v , u) eine Rückwärtskante.
Datenstrukturen und Algorithmen
Graphalgorithmen
Tiefensuche
(Folie 199, Seite 58 im Skript)
Finden von Kreisen
Theorem
Gegeben sei ein gerichteter Graph G . Dann können wir in linearer
Zeit feststellen, ob G azyklisch ist (keine Kreise enthält).
Beweis.
Führe eine Tiefensuche auf G aus.
Behauptung: G ist genau dann azyklisch, wenn es keine
Rückwärtskanten gibt.
⇒ Wenn es eine Rückwärtskante von u nach v gibt, dann gibt es
auch einen Pfad von v nach u im DFS-Wald. Dies ist ein Kreis.
⇐ Angenommen es gibt einen Kreis. Sei u der Knoten auf dem
Kreis mit minimalem d(u) und v der Knoten auf dem Kreis vor u.
Dann gilt d(u) < d(v ) und f (v ) < d(u).
Also ist (v , u) eine Rückwärtskante.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
Übersicht
3
Graphalgorithmen
Darstellung von Graphen
Tiefensuche
Starke Komponenten
Topologisches Sortieren
Kürzeste Pfade
Netzwerkalgorithmen
Minimale Spannbäume
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 200, Seite 58 im Skript)
Starke Zusammenhangskomponenten
Definition
Es sei G = (V , E ) ein gerichteter Graph. Ein Pfad der Länge k von
u1 nach uk+1 ist eine Folge (u1 , u2 ), (u2 , u3 ), . . . , (uk , uk+1 ) von
Kanten aus E wobei u1 , . . . , uk+1 paarweise verschieden sind.
Eine Menge C ⊆ V ist eine starke Zusammenhangskomponente,
wenn es Pfade zwischen allen Paaren von Knoten in C gibt und es
keine echte Obermenge von C mit dieser Eigenschaft gibt.
Die starken Komponenten sind eine Verfeinerung der
Zusammenhangskomponenten des entsprechenden ungerichteten
Graphen.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 200, Seite 58 im Skript)
Starke Zusammenhangskomponenten
Definition
Es sei G = (V , E ) ein gerichteter Graph. Ein Pfad der Länge k von
u1 nach uk+1 ist eine Folge (u1 , u2 ), (u2 , u3 ), . . . , (uk , uk+1 ) von
Kanten aus E wobei u1 , . . . , uk+1 paarweise verschieden sind.
Eine Menge C ⊆ V ist eine starke Zusammenhangskomponente,
wenn es Pfade zwischen allen Paaren von Knoten in C gibt und es
keine echte Obermenge von C mit dieser Eigenschaft gibt.
Die starken Komponenten sind eine Verfeinerung der
Zusammenhangskomponenten des entsprechenden ungerichteten
Graphen.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
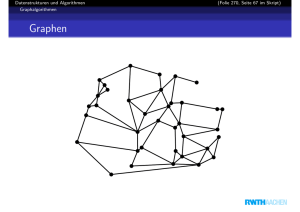
Starke Komponenten – Beispiel
Es gibt genau vier starke Komponenten.
(Folie 201, Seite 58 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 202, Seite 58 im Skript)
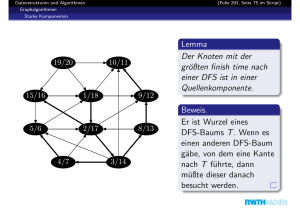
Lemma
Der Knoten mit der
größten finish time nach
einer DFS ist in einer
Quellenkomponente.
Beweis.
Er ist Wurzel eines
DFS-Baums T . Wenn es
einen anderen DFS-Baum
gäbe, von dem eine Kante
nach T führte, dann
müßte dieser danach
besucht werden.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
19/20
15/16
(Folie 202, Seite 58 im Skript)
10/11
1/18
5/6
9/12
2/17
4/7
Lemma
Der Knoten mit der
größten finish time nach
einer DFS ist in einer
Quellenkomponente.
8/13
3/14
Beweis.
Er ist Wurzel eines
DFS-Baums T . Wenn es
einen anderen DFS-Baum
gäbe, von dem eine Kante
nach T führte, dann
müßte dieser danach
besucht werden.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
19/20
15/16
(Folie 202, Seite 58 im Skript)
10/11
1/18
5/6
9/12
2/17
4/7
Lemma
Der Knoten mit der
größten finish time nach
einer DFS ist in einer
Quellenkomponente.
8/13
3/14
Beweis.
Er ist Wurzel eines
DFS-Baums T . Wenn es
einen anderen DFS-Baum
gäbe, von dem eine Kante
nach T führte, dann
müßte dieser danach
besucht werden.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 203, Seite 58 im Skript)
Quellenkomponente:
Starke Komponente, in die
keine Kante hineinführt
19/20
15/16
10/11
1/18
9/12
Senkenkomponente: Starke
Komponente, aus der
keine Kante herausführt
Gr : Wie G , aber Richtung
der Kanten umgekehrt
5/6
2/17
8/13
Korollar
4/7
3/14
Der Knoten mit der
größten finish time nach
einer DFS in Gr ist in einer
Senkenkomponente von G .
Die starken Komponenten von G und Gr sind identisch.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 203, Seite 58 im Skript)
Quellenkomponente:
Starke Komponente, in die
keine Kante hineinführt
19/20
15/16
10/11
1/18
9/12
Senkenkomponente: Starke
Komponente, aus der
keine Kante herausführt
Gr : Wie G , aber Richtung
der Kanten umgekehrt
5/6
2/17
8/13
Korollar
4/7
3/14
Der Knoten mit der
größten finish time nach
einer DFS in Gr ist in einer
Senkenkomponente von G .
Die starken Komponenten von G und Gr sind identisch.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 204, Seite 58 im Skript)
Starke Komponenten
Lemma
Gegeben sei ein gerichteter Graph G mit einem DFS-Wald.
Der DFS-Wald bleibt samt discover und finish times ein möglicher
DFS-Wald, wenn die Quellenkomponente entfernt wird, die den
Knoten mit maximaler finish time enthält.
3/4
7/16
10/15
1/6
18/21
12/13
2/5
8/9
11/14
17/22
19/20
Beweis.
Der Baum spannt die ganze starke Komponente auf. Er wurde als
letzter besucht.
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 205, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
1
Bilde Gr (Kanten umdrehen)
2
Führe Tiefensuche auf Gr aus
3
Ordne die Knoten nach absteigender finish time f (v )
4
Führe in dieser Reihenfolge Tiefensuche auf G aus
5
Jeder Baum im DFS-Wald spannt eine starke Komponente auf
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
2/5
8/9
11/14
17/22
19/20
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
2/5
8/9
11/14
17/22
19/20
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
2/5
8/9
17/22
11/14
19/20
3/4
1/6
2/5
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
2/5
17/22
8/9
11/14
19/20
7/14
8/13
3/4
9/12
10/11
1/6
2/5
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
2/5
17/22
8/9
11/14
19/20
7/14
8/13
3/4
9/12
15/16
10/11
1/6
2/5
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 206, Seite 58 im Skript)
Starke Komponenten – Algorithmus von Kosaraju
3/4
7/16
10/15
1/6
18/21
12/13
17/22
2/5
8/9
11/14
19/20
19/20
7/14
8/13
3/4
17/22
9/12
18/21
15/16
10/11
1/6
2/5
Datenstrukturen und Algorithmen
Graphalgorithmen
Starke Komponenten
(Folie 207, Seite 59 im Skript)
Theorem
Der Algorithmus von Kosaraju berechnet die starken Komponenten
eines gerichteten Graphen.
Beweis.
Die DFS auf G beginnt in einem Knoten einer Senkenkomponente
von G . Dabei entsteht ein DFS-Baum, der diese starke
Komponente aufspannt.
Die DFS fährt dann wieder in einer Senkenkomponente des
Restgraphen fort und so weiter.
19/20
7/14
8/13
17/22
3/4
9/12
18/21
15/16
10/11
1/6
2/5