Vorlesung Ang. Mathematik für BWL 2.Woche: Funktionen I
Werbung

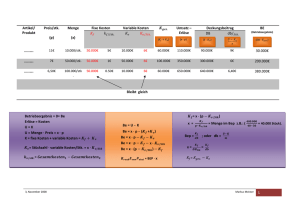
Vorlesung Ang. Mathematik für BWL 2.Woche: Funktionen I Der Funktionsbegriff ist seit ca. 350 Jahren (Leibniz, Newton) einer der bedeutendsten mathematischen Begriffe. Bis vor wenigen Jahrzehnten hat man in der Mathematik und in den Anwendungswissenschaften eine Funktion in erster Linie als Beziehungen zwischen (einer oder mehreren) unabhängigen Variablen und einer davon abhängigen Variablen gesehen (Variablenkonzept). Erst mit der mengentheoretischen Fundierung der Mathematik im 20. Jh. definierte man Funktionen (Abbildungen) als spezielle Art von Zuordnungen zwischen Mengen (Zuordnungskonzept). 2.1 Definition v. Funktion als Zuordnung zw. Mengen: Gegeben seien: S Definitionsmenge (Urbildmenge) A, S Wertemenge (Bildmenge) B, (es kann A=B sein) S Zuordnungsvorschrift f, die jedem x0A genau ein f(x)0B zuordnet. Eine derartige Zuordnungsvorschrift nennt man Funktion (oder Abbildung) von A nach B. Bei Funktionen kommt es also darauf an, dass (i) jedem Element von A ein Element von B zugeordnet wird (ii) jedem Element nur ein einziges Element von B zugeordnet wird. Beachte: C statt x, f, A, B können auch andere Bezeichnungen stehen. C Bedingung (i) kann durch geeignete Reduktion der Menge A immer erreicht werden: man eliminiert aus A alle Elemente, denen kein Element aus B zugeordnet wird. C Bedingung (ii) kann oft durch Reduktion von B erreicht werden. z.B.: f(x) = x ist eine Funktion im oben definierten Sinn, wenn A= ú0+ und B = ú0+. Würde man A=ú und B=ú0+ wählen, dann würde nicht jedem Element aus A ein Element aus B zugeordnet: f wäre dann keine Funktion. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 10 2.4 Darstellungsformen von Funktionen 2.4.1 systemische und symbolische Darstellung: x 6 f(x), y = f(x); K = K(m); E = E(m,p) 2.4.2 Darstellung in Wertetabelle 2.4.3 Funktionsgleichung bzw. Termdarstellung: f(x) = 2x+14: Funktionen als Rechenvorschriften 2.4.4 Graphische Darstellung durch Funktionsgraphen: Funktionen als “Kurven” Die Darstellungsformen 1 und 2 sind sehr allgemein, 3 und 4 hauptsächlich für reelle Funktionen relevant. Verschiedene Darstellungsformen erlauben verschiedene Operationen: symbolische Darstellung: - Hintereinanderausführen von Funktionen (Einsetzen) - Invertieren von Funktionen Tabelle: - Ablesen von bestimmten Funktionswerten - Änderungsverhalten, Maxima, Minima (reellwertige Fu) Funktionsgleichung, Termdarstellung: - Berechnen von Funktionswerten, - Addieren von Funktionen, - Ableitungsfunktion - Ermitteln von Funktionsgraphen - Umformen von Funktionen (ev. auch Invertieren) Funktionsgraph: - Ablesen spezieller Werte - Änderungsverhalten von Funktionen - Vergleich von Funktionen - graph. Invertieren (falls möglich) Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 14 2.5 Spezielle Typen von reellen Funktionen 2.5.1 Betragsfunktion f(x) = |x|: f(x) = x für x>0, und f(x) = -x für x<0 2.5.2 konstante Funktionen: f(x) = c (c beliebige Konstante 0 2.5.3 Treppenfunktionen: stückweise konstante Funktionen. Messungen aller Art führen oft zu Treppenfunktionen. Treppenfunktionen mit “feiner” Treppung (Länge jeder Treppenstufe und Abstand der Stufen relativ klein) werden oft durch “glatte” (=differenzierbare, termdarstellbare) Funktionen approximiert. 2.5.4 lineare Funktionen f(x) = k·x + d mit k, d 0 , k…0 Spezialfall: homogen lineare Funkt: f(x) = k·x k…0, k 0 2.5.5 Potenzfunktionen f(x) = xn; n ganzzahlig (auch n<0!) 2.5.6 allgemeine Potenzfunktion für a = 1/n: Wurzelfunktion f(x) = xa; a 0 2.5.7 Polynomfunktionen f(x) = a·x+b (a,b0 ú , a…0) (Pol. ersten Grades, lineare Fu) f(x) = a·x2+b·x+c (a,b,c0 , a…0) (2. Gr., quadrat. Pol) f(x) = a·x3+b·x2+c·x+d (a,b,c,d 0 , a…0) (Polynome 3. Gr.,) 2.5.8 gebrochen rationale Funktionen f(x) = p1(x)/p2(x) mit p1, p2 Polynome 2.5.9 Exponentialfunktionen f(x) = c·ax = c·ex·ln(a) mit a>0; c…0; e = 2,71828... ax · ay = ax+y 2.5.10 Logarithmusfunktionen f(x) = alog(x) mit a > 0; speziell ln(x) =elog(x) ln(x): “natürlicher Logarithmus” alog(x) = ln(x)/ln(a); alog(1) = 0 alog(a) = 1; x log(x) = x ax und alog sind invers. alog(a ) = x; a alog(x·y) =alog(x) +alog(y) s alog(r ) = s · alog(r) Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 15 2.7 Rechnen mit Funktionen Addition, Subtraktion, Multiplikation, Division von reellen Funktionen erfolgen elementweise: f1 + f2 (x) = f1(x) + f2(x) f1 S f2 (x) = f1(x) S f2(x) f1 · f2 (x) = f1(x) · f2(x) f1 / f2 (x) = f1(x) / f2(x) (für f2 … 0) Voraussetzung: f1, f2 reelle Funktionen, die für dieselben xWerte definiert sind. z.B. f1(x) = 2x; f2(x) = x2; f1+f2(x) = 2x + x2 Addition und Subtraktion von Funktionen ist auch graphisch möglich! z.B. bei der Wilson’schen Formel (opt. Bestellmenge): Wilson'sche Formel 8 7 6 Kosten 5 Fixko/Stk Lagerko/Stk 4 GesKo/Stk 3 2 1 0 0 2 4 6 8 10 12 Menge x Gesamtkosten/Stk = Fixkosten/Stk + Lagerkosten/Stk Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 18 Vorlesung Angew. Mathematik für BWL 3. Woche: Funktionen II 3.1 Funktionen in d. WiWi (Auswahl) Funktionstyp unabh. Variable(n) abh. Variable Einsatzmenge von Prod.Fakt. Produktionsmenge bzw. Ertrag Produktionsmenge Gesamtkosten Absatzmenge Preis pro Stück Preis pro Stück absetzbare Menge Erlösfunktionen Produktionsmenge Gesamterlös Gewinnfunktion Produktionsmenge Gewinn Konsumfunktion Volkseinkommen Konsumausgaben Produktionsfunktion (Ertragsfunktion) Kostenfunktionen Preis-Absatzfunktion Nachfragefunktion 3.1.1 Produktionsfunktionen (Ertragsfunktionen) unabh. Var: Einsatzmenge(n) von Produktionsfaktor(en) abhängige Var.: Produktionsmenge bzw. Ertrag m = f(r1, r2, r3, ... rn) bzw. E = f(r1, r2, r3, ... rn) Sonderfall: nur eine unabh. Variable m = f(r) bzw. E = f(r) (durch ceteris-paribus-Bedingung erreichbar) 3.1.2 Preis-Absatzfunktion p = p(m) unabh. Var.: Nachgefragte Menge eines Monopolgutes abh. Var.: Preis des Gutes - beschreibt Absatz eines Monopolgutes aus der Sicht des Anbieters: Monopolist bestimmt Menge m: am Markt ist ein davon abhängiger Preis p(m) erzielbar Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 22 3.1.3 Nachfragefunktion m = m(p) unabh. Var.: Preis eines Monopolisten abh. Var: am Markt nachgefragte Menge - beschreibt Absatz eines Monopolgutes aus der Sicht der Käufer: Am Markt ist ein Monopolgut zu einem bestimmten Preis p verfügbar. In Abhängigkeit davon wird die Menge m(p) nachgefragt. - ist zur Preis-Absatzfunktion invers 3.1.4 Erlösfunktionen - Erlös = abgesetzte Menge × Preis pro ME; E = m · p - Wenn Preis-Absatzfunktion p = p(m) gegeben ist, dann ist E(m) = m · p(m) mit unabhängige Variable: abgesetzte Menge m abhängige Variable: Gesamterlös (=Umsatz) E 3.1.5 Gewinnfunktion - Gewinn = Gesamterlös – Gesamtkosten; G = E – K - Wenn E und K jeweils als Funktionen der Menge m gegeben sind, dann ist die Gewinnfunktion G(m) = E(m) – K(m) mit unabhängige Variable: Menge m abhängige Variable: Gewinn G(m) z.B. sei K(m) = m3–10m2+40m+50 und Nachfragefunktion p(m) = –12m + 110 Dann ist E(m) = m · p(m) = –12m2 + 110m und damit G(m) = –m3 – 2m2 + 70m – 50 3.1.6 Konsumfunktionen unabhängige Variable: Volkseinkommen Q abhängige Variable: Konsumausgaben C = C(Q) oft lineares Modell: C(Q) = a + c·Q Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 23 a: autonomer Konsum c: marginale Konsumquote: - 0 < c <1; c liegt etwa bei 0,8 ... 0,95 - c gibt an, wieviel von jedem Schilling Volkseinkommen für Konsumzwecke ausgegeben wird. 3.2 Kostenfunktionen K = K(m) unabh. Var: Produktionsmenge m. abh. Var.: Gesamtkosten K(m) 3.2.1 Grundlegende Begriffe aus der Kostentheorie: In der Kostentheorie wird um die Gesamtkostenfunktion ein ganzes System von miteinander zusammenhängenden Begriffen aufgebaut. Hier zeigt sich die Leistungsfähigkeit des Funktionsbegriffes im wirtschaftstheoretischen Kontext. Fixkosten Kf: Kostenanteil, der von der Produktionsmenge m nicht abhängt, also auch bei Menge m = 0 anfällt. variable Kosten Kv: Kostenanteil, der von der Menge abhängt, i.a. eine wachsende Funktion der Menge. Gesamtkosten K: Fixkosten + variable Kosten; K = Kf + Kv Grenzkosten K’: (in etwa) der Kostenzuwachs, den die letzte (oder nächste) produzierte Einheit verursacht. Stückkosten k: Gesamtkosten/Menge; k = K/m; variable Stückkosten kv: kv = Kv/m fixe Kosten je Stück kf: kf = Kf/m. Beachte: die fixen Kosten je Stück sind nicht fix, sondern hängen von m ab! Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 24 Oft interessiert man sich bei der Untersuchung von Funktionen für folgende Frage: wie ändert sich f(x), wenn sich x ändert? Wir nehmen dazu an, dass uns die Änderung von f(x) interessiert, wenn sich x von x0 auf x1 (es sei x0 < x1) ändert. Man kann dann das Änderungsverhalten der Funktionswerte auf verschiedene Weise messen. Wir setzen einfachheitshalber y0 := f(x0); y1 := f(x1) und definieren vier verschiedene Änderungsmaße: absolute Differenz: Änd1 := y1-y0; Differenzenquotient: Änd2 := (y1-y0)/(x1-x0) = Änd1/(x1-x0) prozentuelle Änder.: Änd3 := (y1-y0)/y0 = y1/y0 - 1 = Änd1/y0 Elastizität(skoeff).: Änd4 := (y1-y0)/y0 / (x1-x0)/x0 = = (y1-y0)@x0 / y0@(x1-x0) = Änd2 @ x0/y0 Aufgabe: Berechnen Sie Änd1 bis Änd4 für die Funkt. f1(x) = 2x+5; f2(x)=2x; f3(x)=ln(x) für x0=3 und x1=5 bzw. für x0=2 und x1=3. Was fällt auf? Beachte: C Alle vier Maßzahlen Änd1 bis Änd4 haben eine bestimmte Sachbedeutung und sind in geeigneten Konstellationen sinnvoll interpretierbar. Es gibt also mehr als ein sinnvolles Maß für die Änderung von Funktionswerten. C Änd1 ist ein wenig praktikables Maß, weil es den x-Abstand nicht berücksichtigt. Ein großer Wert für Änd1 muss noch nicht heißen, dass sich die Funktion rasch ändert; es kann einfach sein, dass x0 und x1 sehr weit auseinanderliegen. Änd2 ist demgegenüber ein standardisiertes (normiertes) Maß, das auch Vergleiche von Änderungsraten für verschieden weit auseinanderliegende x-Werte ermöglicht. In ähnlicher Weise ist Änd4 gegenüber Änd3 ein standardisiertes Änderungsmaß für prozentuelle Änderungen. C Bei Funktionen in tabellarischer Darstellung oder in Termdarstellung kann man die zur Berechnung der Änderungsmaße erforderlichen Zahlen xi bzw. yi direkt ablesen oder berechnen. Bei Funktionsgraphen kann man qualitativ direkt sehen, ob die Funktion wächst oder fällt. C Das Änderungsmaß Änd1 kann im Funktionsgraphen als “Höhendifferenz”, Änd2 als Steigung der Verbindungsstrecke der Punkte (x0;y0) und (x1;y1) interpretiert werden. Auch für die Elastizität (Änd4) gibt es eine graphische Interpretation (siehe Abschnitt 5.3) Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 26 3.4 Momentane Änderungsrate - Differentialquotient Zur Berechnung der Änderungsmaße Änd1 bis Änd4 benötigt man stets zwei Wertepaare (x0;y0) und (x1;y1). Damit beziehen sich die Änderungen auch stets auf eine Intervall (x0;x1). Für bestimmte (“glatte”) Typen von Funktionen ist es nun möglich, auch Änderungsmaße zu konstruieren, die nicht für Intervalle, sondern für jeden einzelnen x-Wert definiert sind. Die Grundidee besteht dabei darin, x1 immer näher an x0 zu rücken und dabei zu sehen, was mit dem Änderungsmaß passiert. Für Änd1 ist dieser Versuch wenig erfolgreich, weil immer das Ergebnis lim Änd1'0 herauskommen würde.. x16x0 Wir würden als “momentane” Änderung stets 0 erhalten - ein wenig aussagekräftiges Ergebnis! Berechnet man hingegen lim Änd2 , so ergibt sich in x16x0 vielen Fällen eine sinnvoll interpretierbare momentane Änderungsrate oder Differentialquotient oder erste Ableitung von f in x0. Symbolisch bezeichnet man diese Zahl mit f`’(x0). Dieser momentanen Änderungsrate entspricht geometrisch die Steigung der Tangente1 an den Funktionsgraphen im Punkt (x0;y0). Die moderne Analysis kennt genaue Kriterien, wann eine Funktion f an einer bestimmten Stelle x0 überhaupt differenzierbar ist (d.h. ein f’(x0) existiert). Wir wollen der Einfachheit halber davon ausgehen, dass die von uns betrachteten Funktionen in der Wirtschaftstheorie dann, wenn wir Ableitungen betrachten, auch tatsächlich differenzierbar sind. 1 Verschiedene deutschsprachige BWL-Autoren (z.B. WÖHE 1984, S. 480) meinen im Zusammenhang mit der Steigung der Tangente, dass diese Steigung einer Geraden gleich dem Tangens ihres Neigungswinkels ist. Dies ist jedoch nur dann richtig, wenn eine Einheit auf der Abszisse dieselbe absolute Länge hat wie eine Einheit auf der Ordinate. Für ungleich skalierte Achsen ist diese Aussage falsch und bei fehlenden Skalierungen sinnlos. Beispiel: Der Tangens des Neigungswinkels einer 45° Gerade ist 1. Wenn jedoch die x-Achse in 1-cm-Abständen mit 10; 20; 30;... und die y-Achse in 1-cmAbständen mit 100; 200; 300; ... skaliert ist, dann hat eine Gerade mit 45° Neigung nicht Steigung 1, sondern Steigung 10. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 27 Typische Funktionen in der Ökonomie (siehe dazu auch Hauke/Opitz, Kapitel 2.1 + 2.2) Lineare Preis-Absatz-Funktion : p ( x) = a − bx x = Absatz, Produktionsmenge, p = Preis je Mengeneinheit Lineare Absatz-Preis-Funktion (Umkehrfunktion der Preis-Absatz-Funktion): x( p) = a 1 − p b b x = Absatz, Produktionsmenge, p = Preis je Mengeneinheit Umsatzfunktion/Erlösfunktion U ( x ) = x ⋅ p ( x) U ( p) = p ⋅ x( p) Lineare Kostenfunktion K ( x ) = K fix + k v ⋅ x Kfix = Fixkosten, k v = variable (Stück-)Kosten Stückkosten K ( x) k (x ) = x Gewinnfunktion G( x) = U ( x ) − K ( x) = D( x) − K fix ( x) D(x) = Deckungsbeitrag Stückgewinn g ( x) = p ( x) − k ( x) Produktionsfunktion x = x (v ) v = Rohstoff-/Materialeinsatz mit der Umkehrfunktion v = v (x ) , die den Materialverbrauch angibt Übung: Bearbeiten Sie die Aufgaben 1 und 2. 2. Differentialrechnung bei einer Funktion mit einer Veränderlichen dy (gibt Anstieg einer Tangente im Punkt x an) dx Synonyme: Ableitungsfunktion / Grenzfunktion / Marginalfunktion Ableitung einer Funktion y ′ = f ' ( x) = 5 Übersicht über wichtige spezielle Ableitungsregeln Funktion 1.Ableitung f (x ) = c ⇒ f ' (x ) = 0 f (x ) = x n ⇒ ( f ( x)) n ln f ( x ) ⇒ ⇒ Funktion f (x ) = e x f ' ( x ) = n ⋅ x n−1 f ( x ) = ln x n ⋅ ( f ( x)) n−1 ⋅ f ' ( x) f (x ) = e g ( x) f ′( x) f ( x) f (x ) = g (x ) 1.Ableitung ⇒ f ' ( x) = e x 1 ⇒ f ' (x ) = x ⇒ f ' ( x) = g ' ( x ) ⋅ e g ( x ) f ' (x ) = h( x ) Allgemeine Ableitungsregeln (1) Faktorregel: Ableitung von c ·f(x) (2) Summenregel: Ableitung von f(x)±g(x) (3) Produktregel: Ableitung von f(x) ·g(x) (4) Kettenregel: Ableitung von f(g(x)) f ( x) (5) Quotientenregel: Ableitung von g (x ) Übung: a) Bearbeiten Sie die Aufgaben 3 und 4. b) Bestimme die 1. Ableitung von y= ist ist ist ist c) Bestimme die höheren Ableitungen von c ·f´(x) f´(x) ±g´(x) g(x) · f´(x) +f(x) ·g´(x) f´(g(x)) ·g´(x) g ( x ) ⋅ f ′( x ) − f ( x ) ⋅ g ′( x) g ²(x) ist ( x2 2x4 − 7x (3x ⇒ 2 − 2x ) ) 3 g ' (x ) f ( x ) ⋅ h ' ( x ) ⋅ ln g ( x ) + h( x ) ⋅ g ( x ) g>0 5 . y = 2x 4 + 5x3 + 3x2 + 7 . Ökonomische Interpretation der 1. Ableitung Sie beschreibt näherungsweise die Funktionswertveränderung bei Änderung der unabhängigen Variablen x um 1 Einheit. z.B. K´(x) = Grenzkostenfunktion; sie gibt ungefähr die zusätzlichen Kosten an, die bei der Erhöhung der Produktion um eine Einheit anfallen. Übung: a) Bestimme und zeichne Durchschnitts- und Grenzkostenfunktion von K(x) = 5 +2 x +0,5x2. b) Interpretiere Grenzsteuersatz und Durchschnittssteuersatz, Grenzumsatz, marginale Konsumquote. Analyse von Funktionen mit Hilfe der Ableitung • Monotonie f´(x) ≥ 0 (f´(x) > 0) ∀x∈[a,b] ∈Df ⇒ f(x) ist (streng) monoton wachsend f´(x) ≤ 0 (f´(x) < 0) ∀x∈[a,b] ∈Df ⇒ f(x) ist (streng) monoton fallend Krümmung (Konkavität oder Konvexität) f´´(x) ≥ 0 ∀x∈[a,b] ∈Df ⇒ f(x) auf [a,b] konvex (nach oben geöffnet) ökonomisch: progressiv wachsend, degressiv fallend f´´(x) ≤ 0 ∀x∈[a,b] ∈Df ⇒ f(x) auf [a,b] konkav (nach unten geöffnet) 6 3.6 Ableitung von Funktionen in der Wi-Theorie 3.6.1 Grenzkosten bei Kostenfunktionen Gegeben seien eine Kostenfunktion: m ÷ K(m), ein m0 und zugeordnete Kosten K0=K(m0). Frage: wie ändert sich K, wenn m um 1 EH von m0 auf m1 = m0+1 erhöht wird? (Kostenzuwachs der nächsten/letzten Einheit). Diesen Kostenzuwachs pro ME nennt man in der Wirtschaftstheorie Grenzkosten oder marginale Kosten (engl. marginal cost). Die so definierten Grenzkosten entsprechen (bei ausreichend kleinen ME) in etwa der mathem. Ableitung der Kostenfunktion K’. Nur bei linearen Kostenfunktionen sind die so definierten Grenzkosten exakt gleich der mathematischen Ableitung K’. Beispiel: Sei K(m) = 0,00001m3-0,003m2+0,4m +20 und damit K(79) = 37,81; K(80) = 37,92; K(81) = 38,03 Grenzkosten (m=80) = K(81)-K(80) = 0,11 oder K(80)-K(79) = 37,92 - 37,81 = 0,11 mathem. Ableitungsfunktion: K’(m) = 0,00003m2-0,006m+0,4 K’(80) = 0,11. Wir sehen also an diesem Beispiel: Grenzkosten . K’ (=Differentialquot. dK/dm) 3.6.2 Grenzertrg bei Ertragsfunktionen: Genauso wird für eine Ertragsfunktion r ÷ E(r) der Grenzertrag definiert: Der Grenzertrag ist jener Ertragszuwachs, wenn r um eine Einheit erhöht wird (Ertragszuwachs der letzten/nächsten eingesetzten Einheit von r). Mathematisch ist der Grenzertrag wiederum (näherungsweise) die erste Ableitung der Ertragsfunktion. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 30 3.6.3 Einkommensteuerfunktion S: E ÷ S(E) E: Bruttoeinkommen p.a.; S(E): ESt bei Bruttoeinkommen E Aufgabe: Zeichnen Sie die Funktion E ÷ S(E) für die österreichische Einkommensteuer (EStG 1988, § 33, Abs. 1: Die Einkommensteuer beträgt von dem Einkommen jährlich für die ersten 50.000 S ..10%; für die weiteren 100.000S .. 22%; für die weiteren 150.000S ..32%; für die weiteren 400.000S .. 42%; für alle weiteren Beträge .. 50%.). Grenzssteuersatz S’: wieviel erhöht sich der Steuerbetrag, wenn man brutto um ÖS 1,mehr verdient? Spitzensteuersatz: Grenzsteuersatz der höchsten Steuerstufe, 1997 in Österreich bei 50%. Steuerprogression: Grenzssteuersätze werden für höhere Einkommensklassen immer höher. Durchschnittssteuersatz s: = S(E)/E Der Durchschnittssteuersatz s ist bei progressivem Steuersystem stets s # S’. Dies sieht man aus der letzten Graphik: Die Steigung der Strecke OA entspricht dem Durchschnittssteuersatz, die Steigung der Tangente in A dem Grenzsteuersatz für Einkommen E0. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 31 3.7.3 Ein praktischer Ausweg: C Funktionen in der Wi-Theorie brauchen nicht mit infinitesimaler mathematischer Schärfe betrachtet werden. C Für wirtschaftstheoretische Modelle reicht es, wenn man unter den Grenzkosten (Grenzertrag, Grenzerlös...) den Zuwachs bei der Kosten (Erträge, Erlöse) meint, wenn die unabh. Variable um eine Einheit erhöht wird; bzw. der Differenzenquotient Kostenänderung/Mengenänderung) bei ausreichend kleiner Mengenänderung. C Anders gesagt: Grenzkosten = ∆Kosten/∆Menge (∆:Änderung) bei ausreichend kleiner Mengenänderung ∆Menge. C Noch anders gesagt: wenn man bei Differentialquotienten in WiWi-Texten den Nenner = 1 setzt, dann ist der ganze Jammer mit einem Schlag behoben. Z.B. bei Wöhe (1984): Bei dE/dr nehme man dr = 1 (d.h. Änderung des eingesetzten Faktors um 1) an, und “rettet” damit die (sonst falsche) Gleichungskette dE/dr · dr = dE = E’ C Zusammenfassung: Don’t worry, be happy! Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 34 4.2 Kurvendiskussion von Funktionstermen: 1) 2) Funktionsterm ableiten (ev. auch 2. Ableitung) Wertetabelle anlegen: x f(x) f’(x) f ”(x) Anmerk. -2 -1 0 1 3) Max. Definitionsmenge bestimmen d.h.: Polstellen 4) 5) f(x) = 0 liefert Nullstellen fN(x) = 0 liefert (mögliche) Extrema fO > 0: Minimum; fO < 0: Maximum 6) 7) 8) (dort, wo f nicht def. = Nullstellen des Nenners) ausschließen Oder man eruiert Art des Extremums durch Nachbarwerte aus Tabelle bzw. Graphen. fO = 0 liefert (mögliche) Wendepunkte. Verhalten von f für x64 bzw. x6-4 (Grenzwerte) Funktionen der Art P1/P2 mit Grad P1 $ Grad P2 (P1, P2 Polynome) konvergieren für x64 bzw. x6-4 gegen eine einfachere Funktion, z.B. f(x) = (x2+2)/2x konvergiert für x6±4 gegen 0,5x; weil (x2+2)/2x = 0,5x + 1/x und damit x 2%2 1 ' lim 0,5x% ' 0,5x lim x x64 2x x64 Zeichnen des Funktions-Graphen aus den obigen Informationen 2) - 7) Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 36 4.3 Nichtlineare Optimierung in den WiWi Prinzip: Man beschreibt einen Sachverhalt durch eine Funktion und sucht dann das Extremum dieser Funktion. Beispiel: gegeben sei die Gewinnfunktion g(x) = -0,002x3 +9,621x2+57,78x - 8153800. Bei welcher Menge x ist der Gewinn maximal? Lösung: a) Ermittle gN(x) = -0,006x2+19242x+57,78 b) Setze gN(x) = 0. Dies liefert x1 = –3 und x2 = 3210. c) Ob g(x2) ein Maximum ist, kann man mit Hilfe der zweiten Ableitung oder auch durch benachbarte Werte (man berechne g(3200), g(3210) und g(3220)) herausbekommen. ODER: Man tabelliere x und g(x) mit Excel (mit variablen Tabellenanfang und Schrittweite) und suche in der Tabelle den Maximalwert von g(x) (ev. mehrmals den Tabellenanfang und die Schrittweite verändern!) 4.4 Losgrößenformel (Wilson’sche Formel): Gegeben: m: (gleichmäßige) Nachfrage pro ZE (Stk/ZE) k0: fixe Kosten je Produktionslos (GE) k1: (variable) Kosten je Stück (GE/Stk) h: Lagerkosten pro Stück und ZE (GE/Stk.ZE) Gesucht: x: Losgröße (Produktionsmenge) mit minimalen Gesamtkosten (=Prod.Kost + Lagerkosten) je Stück Annahme: Es werden x Stück in einem Produktionslos produziert, die gleichzeitig ins Lager kommen. Nach x/m ZE ist das Lager aufgebraucht und das nächste Los mit x Stück kommt ins Lager. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 37 Z.B.: m = 1000 Stk/Tag ko: 6000 ÖS/Los h = 3 ÖS/Stk.Tag k1: 0,25 ÖS/Stk Sei: x = 4000 Stk D.h. alle x/m = 4 Tage kommen 4000 Stk ins Lager. Mittl. Lagerdauer/Stk d(x) =: 0,5 · x/m (=2 Tage im Bsp) Lagerkosten/Los L(x) = d(x)·h·x = (hx2)/2m (24.000 ÖS) Gesamtkosten/Los f(x) = k0+k1x+L(x) (31.000 ÖS) Stückkosten g(x) = f(x)/x = k0/x + k1+(hx)/(2m) Bei uns: g(x) = 6000/x + 0,25 + 3x/2000 bzw. g(x) = Fixkosten/Stk + var.K/Stk + LagerK/Stk Minimale Stückkosten erfordert gN(x) = 0 2 gN(x) = -ko/x + h/2m = 0 liefert xopt = 2mk0 h 4.4.1 Losgrößenformel bei Wöhe (1984, S 416ff) Wöhe verwendet einen etwas anderen Ansatz, der zum selben Ergebnis führt: Gegeben: M: Verkauf (=Nachfrage pro Jahr) ( ~m) Kf: Fixkosten je Los (~k0) Kl: Lagerkosten pro Stk u. Jahr (~h) Gesucht: m: optimale Losgröße (~x) Wöhe ermittelt die gesamten fixen Kosten KF und die gesamten Lagerkosten KL pro Jahr und minimiert deren Summe K = KF+KL Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 38 Anwendung des logistischen Wachstums: 4.9 Produktlebenszyklusmodelle 4.9.1 Fünf Phasen im Produktlebenszyklus: 1) Einführung: wenig Umsatz, viel Werbeaufwand, kein Gewinn 2) Wachstum: große abs. Zuwächse, Break-Even 3) Reife: Umsatz erreicht Maximum, hohe Gewinne 4) Sättigung: Markt gesättigt: Umsätze stagnieren 5) Degeneration: Produkt läuft aus, verschwindet vom Markt. Ossimitz: Vorlesung Ang. Mathematik für Betriebswirte VOFL98_1 Seite 44