Lehrgang Elektrotechnik 1

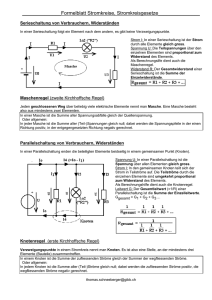
Lehrgang : ELEKTROTECHNIK 1
Arbeitsblatt Nr. 13 :
Name:
ET1-13-F.DOC - 13.11.02
Knotenpunkt- und Maschen-Regel nach Kirchhoff *
*Gustav Robert Kirchhoff wurde am 12. März 1824 in Königsberg geboren. Nach dem Studium der Naturwissenschaften wurde er 1850
Physik-Professor in Breslau. 1854 wechselte er nach Heidelberg und 1875 nach Berlin an die Universität. Bereits in den ersten Jahren seiner
Forschertätigkeit beschäftigte sich Kirchhoff mit den Erscheinungen und Gesetzen der Elektrizität. Er knüpfte an die Erkenntnisse von Georg
Simon Ohm (1789 – 1854) an und stellte im Jahr 1854 die beiden nach ihm benannten Kirchhoffschen Regeln der elektrischen Stromkreise auf.
Von großer Bedeutung für die Astronomie und Physik wurden Kirchhoffs experimentelle Untersuchungen der Emission und Absorption des Lichtes, die er in den Jahren 1859 und 1860 zusammen mit dem Chemie-Professor Robert Wilhelm Bunsen (1811 – 1899) durchführte. Die dabei
gewonnenen Erkenntnisse führten zur Erklärung der Fraunhoferschen Linien des Sonnenspektrums, zur Begründung der Spektralanalyse und zur
Aufstellung des Kirchhoffschen Strahlungsgesetzes. Kirchhoff starb am 17. Oktober 1887 im 64. Lebensjahr in Berlin.
™
1.
Knotenpunkt-Regel (1. Kirchhoffsche Regel)
Ι3
Ι1
Ι4
n
∑ Ik = 0
k =1
In jedem Stromverzweigungspunkt ist die Summe aller
Ströme unter Beachtung der Vorzeichen stets gleich Null.
Ι2
• Für den Knotenpunkt in Bild 1 gilt demnach:
zufließende
Ströme (+)
n
∑ Ik = I1 + I2 + ( −I3 ) + ( − I4 ) + ( −I5 ) = 0
k =1
⇒ I1 + I 2 − I3 − I 4 − I5 = 0
⇒
™
2.
zufließenden
n
∑ Uk = 0
k =1
abfließend
Ströme ist stets gleich der Summe der
Maschen-Regel (2. Kirchhoffsche Regel)
U1
U7
R6
U4
U5
Ι7
Ι1
R3
U3
M1
U6
Ströme.
Ι3
U2
Umlaufrichtung in
der Masche
Ι6
positives Vorzeichen, Spannungen gegen die Umlaufrichtung ein negatives Vorzeichen.
Ι2
R2
• Spannungen in Umlaufrichtung der Masche erhalten ein
• Damit gilt in der Masche M1 (Bild 2):
abfließenden
Ι8
In jedem geschlossenen Stromkreis
(Masche) ist die Summe der Spannungen unter Beachtung der Vorzeichen stets gleich Null.
• Die Umlaufrichtung in einer Masche ist frei wählbar.
abfließende
Ströme (–)
Bild 1: Knotenpunkt in einem
Netzwerk
I1 + I 2 = I3 + I 4 + I5
12
4
4
3 14243
zufließend
• Fazit: Die Summe der
Ι5
Ι5
R5
Ι4
Bild 2: Masche in einem Netzwerk
U1 – U2 – U3 + U4 + U5 + U6 – U7 = 0
• Anwendungsbeispiel: Brückenschaltung
Ι1
Masche M1 :
U1 + UAB – U3 = 0
R2
A
U1
⇒
U2
UAB = U3 – U1
M1
Masche M2 :
U2 – U4 – UAB = 0
R1
⇒
M2
U AB
U3
UAB = U2 – U4
U4
C
Masche M3 :
U3 + U4 – U0 = 0
D
Ι3
⇒
U0 = U3 + U4
⇒
Ι = Ι1 + Ι3
Ι
R3
B
R4
M3
Knotenpunkt C :
Ι – Ι1 – Ι3 = 0
U0
Lehrgang : ELEKTROTECHNIK 1
Name:
ET1-13A.DOC - 16.11.03
Arbeitsblatt Nr. 13 a) : Schaltungen von elektrischen Widerständen (Wiederholungsübung)
• Übungsaufgaben: Gruppenschaltungen von Widerständen (gemischte Schaltungen)
Ι1
1. Berechnen Sie für die nebenstehende Widerstandsschaltung
R1
R3
A
Ι3
a) den Gesamtwiderstand Rges ,
80 Ω
Ι2
b) die Ströme Ι 1 , Ι 2 und Ι 3 und
U = 220 V
R2
R4
5Ω
10 Ω
c) die Spannung UAB zwischen den Punkten A und B.
4Ω
R6
[110 Ω ; 2 A – 1,6 A – 0,4 A ; 8 V]
Ι
2. Berechnen Sie für die nebenstehende Widerstandsschaltung
R5
26 Ω
B
R1
A
6Ω
R3
10 Ω
a) den Strom Ι und
b) die Spannung UAB zwischen den Punkten A und B.
12 Ω
U=
R2
R5
R4
130 V
15 Ω
60 Ω
18 Ω
[13 A ; 86,67 V]
B
Ι1
3. Berechnen Sie für die nebenstehende Widerstandsschaltung
a) den Gesamtwiderstand Rges und
R1
Ι2
12 Ω
45 Ω
R3
[62,3 Ω ; 1,35 A – 134,4 mA – 112 mA]
C
R2
24 Ω
U = 100 V
b) die Ströme Ι 2 , Ι 6 und Ι 7 .
R4
A
Ι6
Ι7
R6
60 Ω
R7
72 Ω
R5
30 Ω
54 Ω
B
4. Der Gesamtwiderstand der nebenstehenden Widerstandsschaltung beträgt Rges = 5,55 Ω.
D
R1
R4
5Ω
7,5 Ω
a) Zeichnen Sie die Schaltung so um, daß Reihen- und
Parallelschaltungen zweifelsfrei erkennbar sind.
R5
4,5 Ω
R3
b) Berechnen Sie den Widerstand R3 .
[15 Ω]
R2
R6
10 Ω
3Ω
Ι ges
U = 10 V
5. Gegeben ist die nebenstehende Widerstandsschaltung.
a) Zeichnen Sie die Schaltung so um, daß
Reihen- und Parallelschaltungen zweifelsfrei
erkennbar sind.
b) Berechnen Sie den Gesamtwiderstand Rges
der Schaltung.
c) Berechnen Sie die Spannungen an den
Widerständen R1 , R3 und R7 .
[2,4 Ω ; 1,5 V – 7,5 V – 4,5 V
R5
A
R1
R2
1Ω
2Ω
3Ω
B
U = 12 V
R3
R4
R6
5Ω
6Ω
2Ω
R7
C
3Ω
Lehrgang : ELEKTROTECHNIK 1
1.
ET1-14-F.DOC - 17.11.02
Ermittlung von Knotenpunkt- und Maschengleichungen
Arbeitsblatt Nr. 14 :
™
Name:
Seite
1
Ermittlung der Anzahl der möglichen Knotenpunktgleichungen (n) und der erforderlichen Maschengleichungen (k) für die Berechnung eines Gleichstrom-Netzwerkes
• Bezeichnet man mit m die Anzahl der Knotenpunkte in einem Netzwerk und mit i die Anzahl der unbekannten Zweigströme (und damit auch die Anzahl der erforderlichen Gleichungen), dann ermöglichen
u
n = m – 1 Knotenpunkte die Aufstellung von n voneinander unabhängigen
Knotenpunktgleichungen und
u
k = i – n Maschen die Aufstellung von k voneinander unabhängigen Maschengleichungen.
• Beispiel: Die Zweigströme in dem unten dargestellten Netzwerk sollen berechnet werden.
i
m
n
k
u Unbekannte Zweigströme im Netzwerk:
u Knotenpunkte im Netzwerk:
u Mögliche Knotenpunktgleichungen:
u Erforderliche Maschen und Maschengleichungen:
™
2.
= 10
= 6
= 6 – 1 = 5
= 10 – 5 = 5
Verfahren zur Ermittlung von Maschen, die eine Aufstellung voneinander unabhängiger Maschengleichungen ermöglichen
1. Sämtliche Knotenpunkte werden über den »vollständigen Baum« miteinander verbunden.
Achtung: Die Zweige des Baumes dürfen an keiner Stelle in sich geschlossene Maschen bilden!
2. Die verbleibenden Verbindungen zwischen den Knotenpunkten bilden das
»System der unabhängigen Zweige«.
3. Die Festlegung der Maschen erfolgt nach folgendem Verfahren:
a) Immer von einem unabhängigen Zweig ausgehen und dann
b) den Zweig über den vollständigen Baum zu einer Masche schließen.
Wichtiger Hinweis: Nie zweimal über einen unabhängigen Zweig gehen!!!
Ι2
Ι3
B
Ι4
M1
R2
A
Ι1
U1
R4
R1
M2
Ι5
R5
C
U2
R3
Ι6
Ι 10
Spannungen:
M3
R6
R12
U 1 = 60 V
U 2 = 80 V
R10
U 3 = 80 V
M5
D
Ι8
U3
R8
Ι7
R7
M4
E
R 1 ... R 12 = 10 Ω
R9
Ι9
R 11
Ι 10
F
Vgl.: Moeller/Frohne u.a., Grundlagen der Elektrotechnik, Stuttgart 1996 (18. Auflage), S.83
Widerstände:
vollständiger Baum
unabhängige Zweige
Maschen
Lehrgang : ELEKTROTECHNIK 1
3.
ET1-14-F.DOC - 17.11.02
Ermittlung von Knotenpunkt- und Maschengleichungen
Arbeitsblatt Nr. 14 :
™
Name:
Seite
2
Beispiel: Gleichstrom-Netzwerk mit 10 unbekannten Zweigströmen
Ι2
Ι3
B
Ι4
M1
R2
A
Ι1
R4
R1
U1
M2
Ι5
R5
C
U2
R3
Ι6
Ι 10
Spannungen:
M3
R6
U 1 = 60 V
R12
U 2 = 80 V
R10
U 3 = 80 V
M5
D
Ι7
Ι8
U3
R8
Widerstände:
E
R7
R 1 ... R 12 = 10 Ω
R9
M4
vollständiger Baum
unabhängige Zweige
Ι9
R 11
Ι 10
Maschen
F
a) 5 Knotenpunktgleichungen
A. + I1 − I 2
B.
+ I2
C. − I1
D.
E.
+ I10
− I3
− I4
+ I4
+ I3
+ I5
− I6
+ I6
− I5
− I7
+ I7
=0
=0
=0
=0
=0
− I8
+ I9
b) 5 Maschengleichungen
+ R1 ⋅ I1 + R 2 ⋅ I2
+ R 3 ⋅ I3 − R 4 ⋅ I 4
+ R 4 ⋅ I4
− R 6 ⋅ I6
M 3 − ( R 5 + R12 ) ⋅ I5 − R 6 ⋅ I6
M4
+ R 7 ⋅ I 7 − R 8 ⋅ I8
M5
− R1 ⋅ I1 + R 6 ⋅ I6
− R 7 ⋅ I7
− R 9 ⋅ I9
+ R 8 ⋅ I8
M1
M2
− U1 = 0
=0
− R 7 ⋅ I7
+ U2
+ ( R10 + R11 ) ⋅ I10
+ U1 − U 3
Ergebnisse
Ι1
=
2,2
A
Ι4
=
0,6
A
Ι7
=
0,6
A
Ι2
=
3,2
A
Ι5
=
3,0
A
Ι8
=
0,8
A
Ι3
=
2,6
A
Ι6
=
1,4
A
Ι9
=
– 0,2
A
Ι 10
=
1,0
A
=0
=0
=0
Lehrgang : ELEKTROTECHNIK 1
Name:
ET1-15-1.DOC - 17.11.02
Berechnung von Gleichstrom-Netzwerken (Übungen)
Arbeitsblatt Nr. 15 :
• Aufgabe :
Ι1
1. gegeben :
U1 = 10 V
U2 = 20 V
U3 = 10 V
Berechnen Sie bei allen Aufgaben dieses Arbeitsblattes die
jeweils gesuchten Zweigströme
mit Hilfe der Knotenpunkt- und
der Maschenregel.
Ι3
A
Ι2
+
U1
R1 = 5,0 Ω
R2 = 12,5 Ω
R3 = 5,0 Ω
+
U2
+
R1
R2
U3
R3
gesucht :
I2 = ?
Lösung: I 2 = 2 A
2.
B
gegeben:
U1
R1 bis R7 = 5 Ω
Ι3
Ι1
R1
U1 = U2 = U3 = 210 V
U3
Ι5
A
Ι2
gesucht:
I1 = ?
I2 = ?
R4
R2
R5
R3
Lösung:
U2
I1 = 4 A
I2 = 8 A
Ι6
B
3.
gegeben:
gesucht:
Ri1 = Ri2 = 5 Ω
I1 = ? I2 = ?
I3 = ?
R1 = 10 Ω
R2 = 20 Ω
R3 = 10 Ω
R4 = 20 Ω
U1 = 200 V
U2 = 100 V
C
R6
R1
I1
R7
A
I3
I2
R i1
R3
R2
R4
U1
Lösung:
I1 = 3,125 A
I2 = 1,875 A
I3 = 1,250 A
U2
4.
R1
gegeben:
R1 = 10 Ω
R4 = 20 Ω
R2 = 30 Ω
R5 = 5 Ω
U1 = 100 V
U2 = 150 V
gesucht:
R3 = 5 Ω
R6 = 20 Ω
B
R i2
Ι1
A
Ι4
R4
Ι3
R7 = 2 Ω
U1
U2
R3
R2
Sämtliche Zweigströme !
R7
Ι7
Ι5
D
Lösung:
B
C
I1 = – 1,712 A
I3 = 6,277 A
I4 = – 4,565 A
I5 = 3,652 A
I6 = 0,913 A
I7 = – 2,625 A
Ι6
R6
R5
Arbeitsblatt Nr. 15
Lösung
1
Ι1 +
Ι2 –
2
Ι1 +
Ι2
3
2 Ι1 –
Ι2
zu Aufgabe 2
Ι3
Ι1 +
2+4
Ι1 +
3
2 Ι1 –
2+4 = 2'
2 Ι3
–
Ι5
= – 42 A
Ι3
–
Ι5
= 0
+
Ι5
+
+
Ι2
Ι6 = + 42 A
·2
0 = + 42 A
= 0
2 Ι3
–
Ι5
= – 42 A
2 Ι1 +
2
Ι2 – 2 Ι3
–
2 Ι5
Ι1 +
2
Ι2
+
Ι5
–
Ι5
= – 42 A
= – 42 A
2 Ι1 –
3
Ι5
Ι2
5
1
+
Ι2 –
2
Ι6 = 0
= 0
5
1
= 0
–
Ι2
4
Ι5
–
= 0
+
Ι2
0 = + 42 A
= 0
2 Ι3
5
1+5 = 1'
2 Ι1 +
2
Ι2 + 0
–
3 Ι5
2+4 = 2'
Ι1 +
2
Ι2
+
Ι5
+
Ι2
0 = + 42 A
3
2 Ι1 –
1+5 = 1'
2 Ι1 +
2
Ι2 + 0
–
3 Ι5
= – 42 A
2+4 = 2'
3 Ι1 +
6
Ι2
+ 3 Ι5
= + 126 A
3
2 Ι1 –
1'+2' = 1''
5 Ι1 +
3
2 Ι1 –
1'+2' = 1''
5 Ι1 +
8
Ι2
3
16 Ι1 –
8
Ι2
1''+3
21 Ι1 +
0
= 0
Ι2
8
= 0
Ι2
= + 84 A
+ 0
Ι2
= 0
= 0
= + 84 A
21 Ι1 = +
84 A
Ι1 = +
4,0 A
5 Ι1 +
8
Ι2
= + 84 A
+
8
Ι2
= + 64 A
Ι2 = +
U1
I3
R1
I1
U3
I5
A
I2
R4
·8
= + 84 A
+ 0
+
1''
·3
R2
R5
8,0 A
R1 =
5Ω
R4 =
5Ω
U1 = 210 V
R2 =
5Ω
R5 =
5Ω
U2 = 210 V
R3 =
5Ω
R6 =
5Ω
U3 = 210 V
R7 =
5Ω
R3
U2
I6
B
R6
C
R7
ET1-15-2.xls - 05.12.02
Lehrgang : ELEKTROTECHNIK 1
• Überlagerungssatz nach Hermann v. HELMHOLTZ (1821-1894)
Ι3
A
Helmholtz ging von der Annahme aus, daß sich der Zweigstrom in
jedem Maschenzweig eines Netzwerkes zusammensetzt aus einer
Summe von fiktiven Teilströmen, wobei jede Spannungsquelle für sich
betrachtet in jedem Zweig einen dieser fiktiven Teilströme erzeugt.
Ι2
U1
U2
U3
12 V
24 V
72 V
R1
R2
R3
3Ω
6Ω
6Ω
™
1.
Der tatsächliche Zweigstrom in einem Maschenzweig ergibt sich aus
der Überlagerung dieser fiktiven Teilströme, wobei bei deren Addition
die jeweilige Stromrichtung durch entsprechende Vorzeichensetzung
zu berücksichtigen ist.
Zur Darstellung dieses Verfahrens sollen die Zweigströme in dem nebenstehenden Schaltungsbeispiel berechnet werden.
B
Berechnung der fiktiven Teilströme nur mit U1 (Dazu werden U2 und U3 kurzgeschlossen.)
I'1
I'3
A
R 'ges = R1 +
I'2
U1
U2
U3
=0V
=0V
12 V
™
2.
R1
R2
R3
3Ω
6Ω
6Ω
3.
4.
I1' , I'2 und I'3
I1' =
U1
R 'ges
;
U 'AB = I1' ⋅ R 23
I'2 =
U 'AB
R2
;
I'3 =
sind die Teilströme,
die nur mit U1
erzeugt würden.
U 'AB
R3
Berechnung der fiktiven Teilströme nur mit U2 (Dazu werden U1 und U3 kurzgeschlossen.)
I''1
I''3
A
R ''ges = R 2 +
U1
U2
U3
=0V!
24 V
=0V!
R1
R2
R3
3Ω
6Ω
6Ω
R1 ⋅ R 3
R1 + R 3
I1'' , I''2 und I''3
I''2 =
U2
R ''ges
;
U ''AB = I''2 ⋅ R13
I1'' =
U ''AB
R1
;
I3'' =
sind die Teilströme,
die nur mit U2
erzeugt würden.
U ''AB
R3
B
Berechnung der fiktiven Teilströme nur mit U3 (Dazu werden U1 und U2 kurzgeschlossen.)
I'''
1
I'''
3
A
R '''ges = R 3 +
I'''
2
™
R 2 ⋅ R3
R 2 + R3
B
I''2
™
ET1-16-F.DOC - 02.12.03
Überlagerungsverfahren nach HELMHOLTZ (Superpositionsmethode)
Arbeitsblatt Nr. 16 :
Ι1
Name:
U1
U2
U3
=0V!
=0V!
72 V
R1
R2
R3
3Ω
6Ω
6Ω
R1 ⋅ R 2
R1 + R 2
I1''' , I'''2 und I'''3
I3''' =
U3
R '''ges
;
U '''AB = I3''' ⋅ R12
I1''' =
U '''AB
R1
;
I'''2 =
sind die Teilströme,
die nur mit U3
erzeugt würden.
U '''AB
R2
B
Überlagerung der Teilströme zur Ermittlung der tatsächlichen Zweigströme
I'3
I1
I'1
I''1
I'''
1
A
I3
I2
I'2 I''2 I'''
2
I''3
I'''
3
d i d i
= d − I i + I + d− I i
= d − I i + d− I i + I
I1 = I1' + − I1'' + − I1'''
I2
I3
'
2
'
3
''
2
'''
2
''
3
'''
3
Teilströme mit gleicher Richtung
wie der jeweilige Zweigstrom erhalten ein positives, die mit entgegengesetzter Richtung ein
negatives Vorzeichen.
Ι2
Ιa
U1
M1
+
Ι5
A
Ιb
R2
M2
B
Ι3
Sofern in einem Zweig mehr als ein Kreisstrom angenommen wurde, werden die
Zweigströme durch Überlagerung der Kreisströme ermittelt. In den übrigen
Zweigen ist der Zweigstrom jeweils der Kreisstrom.
Ι4
Ιc
R3
M3
R4
zu 4. Maschengleichungen für das Netzwerk-Beispiel
ƒ Masche M1 mit dem Kreisstrom Ι a (Die Richtung von Ι a ist hier die positive.)
R 1 ⋅ I a − U1 + U 2 + R 2 ⋅ ( I a + I b ) = 0
U2
+
C
Ι6
ƒ Masche M2 mit dem Kreisstrom Ι b (Die Richtung von Ι b ist hier die positive.)
D
• Das Kreisstromverfahren
2. Festlegung unabhängiger Maschen
Die Bestimmung voneinander unabhängiger Maschen sollte mit Hilfe des "vollständigen Baumes" erfolgen.
3. Zuordnung von Kreisströmen (auch: Maschenströme)
Jeder Masche wird ein Kreisstrom zugeordnet. Auch deren Richtung kann beliebig
festgelegt werden. Die gewählte Kreisstromrichtung wird in der jeweiligen Masche
als positive Stromrichtung angenommen.
4. Aufstellen der Maschengleichungen mit den Kreisströmen
Das Aufstellen der Maschengleichungen erfolgt gemäß der Maschenregel. Die
Spannungsabfälle sind als Produkt anzugeben aus dem Widerstand und dem Kreisstrom, der durch den jeweiligen Widerstand "fließt" (z.B.: R1 · Ι a in der Masche
M1 oder R4 · Ι c in der Masche M3). Falls durch einen Widerstand mehrere
Kreisströme "fließen", so müssen bei der Berechnung des Spannungsabfalls
sämtliche Kreisströme und ihre Richtungen berücksichtigt werden (z.B.:
R2 · (Ι a + Ι b ) in der Masche M1 oder R3 · (Ι b – Ι c) in der Masche M2).
5. Berechnung der Kreisströme
Durch Auflösung des Maschengleichungsystems z.B. mit Hilfe des Additionsverfahrens werden die unbekannten Kreisströme berechnet.
hier die positive.)
R 3 ⋅ (I c − I b ) + R 4 ⋅ I c = 0
zu 6. Ermittlung der Zweigströme für das Netzwerk-Beispiel
ƒ Zweige mit nur einem Kreisstrom
Ι1 = Ιa
Ι4 = Ιc
Ι5 = Ιb
Ι6 = Ιb
ƒ Zweige mit mehreren Kreisströmen (Überlagerung)
Ι1
Ιa
Ι5
A
Ι2
Ιb
Bild 1
Ι 2 = (– Ι a) + (– Ι b)
siehe Bild 1
Ι 3 = (Ι b) + (– Ι c)
siehe Bild 2
Ι5
Ιb
• Beispiel:
Berechnen Sie sämtliche Zweigströme des
Netzwerk-Beispiels. Gehen Sie dabei von
folgenden Werten aus:
U1 = 75 V
U2 = 90 V
R1 = 2,1 Ω
R2 = 2,8 Ω
R3 = 140 Ω
R4 = 120 Ω
Ι4
B
Ι3
Ιc
Bild 2
ET1-17-F.DOC - 17.11.02
Name :
Die Richtungen der Zweigströme können beliebig festgelegt werden. Sofern die
gewählte Stromrichtung mit der tatsächlichen Stromrichtung nicht übereinstimmt, so
ergibt sich bei der Berechnung für den jeweiligen Zweigstrom ein negativer Wert.
ƒ Masche M3 mit dem Kreisstrom Ι c (Die Richtung von Ι c ist
Das Kreisstromverfahren
1. Festlegung der Richtungen der Zweigströme
U 2 + R 2 ⋅ (I b + I a ) + R 3 ⋅ (I b − I c ) = 0
Lehrgang : ELEKTROTECHNIK 1 .
Ι1
R1
6. Ermittlung der Zweigströme
(Beispiel mit 6 Zweigströmen)
Arbeitsblatt Nr. 17 :
• Netzwerk
Lehrgang : ELEKTROTECHNIK 1
ET1-18.DOC - 17.11.02
Übungen zum Kreisstromverfahren
Arbeitsblatt Nr. 18 :
1.
Name:
I2
Lösung:
2.
R6
+
b) Berechnen Sie die Spannung UXY zwischen X und Y.
I5
UXY = – 50 V
+
+
I4
U4 +
R3
U2
R4
+
X
Die nebenstehende Schaltung mit den Spannungen U1 = 9 V und U2 = 12 V
enthält die Widerstände R1 = 2,4 Ω , R2 = 1 Ω , R3 = 2 Ω , R4 = 3 Ω und
R5 = 5 Ω .
+
U1
Ι1
R1
Ι4
R4
Berechnen Sie mit Hilfe des Kreisstromverfahrens sämtliche Zweigströme.
Ι3
R5
Lösung:
Ι 1 = 1,0 A
Ι 4 = 2,2 A
Ι 2 = 3,0 A
Ι 5 = 1,8 A
U3
U5
R5
R2
Ι 3 = 2,00 A
Ι 6 = 0,75 A
Y
I6
I1
Ι 2 = 3,25 A
Ι 5 = 0,50 A
I3
U1
a) Berechnen Sie mit Hilfe des Kreisstromverfahrens sämtliche
Zweigströme.
Ι 1 = 2,75 A
Ι 4 = 1,25 A
I1
R1
In der nebenstehenden Schaltung mit den Spannungen
U1 = 10 V, U2 = 50 V sowie U3 = U4 = U5 = 20 V
beträgt jeder einzelne Widerstand 10 Ω.
Ι5
R3
Ι 3 = 1,2 A
Ι2
R2
+
U2
3.
Ι1
R1
Von dem nebenstehenden Netzwerk sind
folgende Daten bekannt:
Ι4
A
Ι5
U1 = 100 V
U2 = 150 V
U3 = 200 V
R1 = 10 Ω
R2 = 20 Ω
R3 = 30 Ω
R4 = 40 Ω
R5 = 50 Ω
R6 = 60 Ω
R7 = 70 Ω
R8 = 80 Ω
R9 =
1Ω
R2
C
Ι9
U1
R9
U3
+
B
Ι6
Ι2
Berechnen Sie mit Hilfe des Kreisstromverfahrens sämtliche Zweigströme.
Lösung:
Ι 2 = – 1,58 A
Ι 5 = + 3,47 A
Ι 8 = – 0,66 A
Ι 3 = – 1,50 A
Ι 6 = – 0,74 A
Ι 9 = + 4,21 A
Ι8
D
Ι7
+
R4
R8
F
E
Berechnen Sie den Zweigstrom Ι 4 des nebenstehenden
Netzwerks. Gehen Sie von folgenden Daten aus:
U1 = 4,5 V
U2 = 6,0 V
U3 = 7,5 V
R1 = 3 Ω
R2 = 5 Ω
R3 = 4 Ω
Lösung: Ι 4 = 0,694 A
U2
R5
Ι3
4.
R7
R6
R3
Ι 1 = + 2,63 A
Ι 4 = – 0,84 A
Ι 7 = – 0,08 A
+
R1
R2
U1
R3
R4 = 1 Ω
U3
U2
I4
R4
Arbeitsblatt
Nr. 18
Aufgabe 3
Lösung mit dem Gaußschen Eliminationsverfahren
M1
R1 Ι a
+
R2 (Ιa –
Ιc) + R9 (Ιa –
Ιb )
M2
R9 (Ιb – Ιa)
+
R6 (Ιb –
Ιc) + R4 (Ιb –
Ιd)
+ R3 Ι b
= + U1
Ιa = Ι1
R1 = 10 Ω
R5 =
50 Ω
R9 =
= – U1
Ιb = Ι2
R2 = 20 Ω
R6 =
60 Ω
U1 = 100 V
M3
R5 (Ιc – Ιd)
+
R4 (Ιc –
Ιd)
+ R8 Ι c
= – U2
Ιc = Ι3
R3 = 30 Ω
R7 =
M4
R5 (Ιd – Ιc)
+
R6 (Ιd –
Ιb) + R2 (Ιd –
Ιa)
+ R7 Ι d
= + U2 – U3
Ιd = Ι4
R4 = 40 Ω
R8
M1
31 Ιa
–
–
20
Ιd
= + 100 A
: 31
M2
– Ιa
+
131
Ιb
–
Ιc
–
60
Ιd
= – 100 A
· (–1)
–
40
Ιb
+ 170 Ιc
–
50
Ιd
= – 150 A
–
60
Ιb
–
Ιc
+
200
Ιd
= –
M3
M4 – 20
Ιa
Ιb
M1
Ιa
–
0,03
Ιb
M2
Ιa
–
131
Ιb
–
M3
40
Ιb
M4
Ιa
+
3
Ιb
M1
Ιa
–
0,03
Ιb
+
40
50
40
Ιc
+ 170 Ιc
+ 2,5 Ιc
130,97
Ιb
–
M3
–
40
Ιb
+ 170 Ιc
M1-M4
–
3,03
Ιb
–
–
0,03
Ιb
M1-M2
M1
Ιa
40
2,5
Ιc
Ιc
= + 3,23 A
Ιd
= + 100 A
Ιa
–
60
50
Ιd
= – 150 A
Ιd
= + 2,5 A
C
– 0,65 Ιd
= + 3,23 A
Ι2
–
10
– 60,65 Ιd
= – 96,8 A
: 130,97
Ιd
= – 150 A
: (–40)
+ 9,35 Ιd
= + 0,73 A
: (–3,03)
– 0,65 Ιd
= + 3,23 A
–
50
Ιb
– 0,31
Ιd
= – 0,74 A
2
Ιb
– 4,25 Ιc
+ 1,25 Ιd
= + 3,75 A
3
Ιb
+ 0,83 Ιc
– 3,09 Ιd
= – 0,24 A
– 0,65 Ιd
= + 3,23 A
– 0,31 Ιc
– 0,46 Ιd
= – 0,74 A
Ιa
–
0,03
Ιb
Ιb
1
–
0,46
Ι4
R2
R9
Ι9
Ιd
+
Ι6
Ιb
Ι8
D
Ι7
+
Ιc
R4
Ι3
F
E
– 1,71 Ιd
= – 4,49 A
: 3,94
+ 2,62 Ιd
= – 0,5 A
: (–1,13)
– 0,65 Ιd
= + 3,23 A
Ι1 = Ιa
Ι5
=
Ιa + (−Ιd)
Ιb
Ιb
Ermittlung der Zweigströme durch Überlagerung der Kreisströme
– 0,31 Ιc
– 0,46 Ιd
= – 0,74 A
Ι2 = Ιb
Ι6
=
Ιb + (−Ιd)
a
Ιc
– 0,43 Ιd
= – 1,14 A
Ι3 = Ιc
Ι7
=
Ιb + (−Ιc)
b
Ιc
– 2,32 Ιd
= + 0,44 A
Ι4 = Ιd
Ι8
=
Ιc + (−Ιd)
– 0,65 Ιd
= + 3,23 A
– 0,31 Ιc
– 0,46 Ιd
= – 0,74 A
Ιc
– 0,43 Ιd
= – 1,14 A
Ιd
= – 1,58 A
Ιd
= – 0,84 A
1
M1
1
a
a–b
Ιa
–
0,03
Ιb
Ιb
1,89
R5
R8
– 1,13 Ιc
0,03
U2
M3
+ 3,94 Ιc
–
R7
R6
1–3
Ιa
U3
B
M2
R3
+
M4
U1
1–2
M1
U2 = 150 V
U3 = 200 V
Ι5
– 0,65 Ιd
+
70 Ω
80 Ω
A
: (–20)
M1
1
M1
Ιc
50 A
Ι1
R1
=
1Ω
: 1,89
ET1-18-3.XLS - Querformat - 20.11.02
Lehrgang : ELEKTROTECHNIK 1
1.
ET1-19-F.DOC - 25.02.04
Dreieck-Stern-Umwandlung (und umgekehrt)
Arbeitsblatt Nr. 19 :
™
Name:
™
Dreieck- und Stern-Schaltung
2.
Prinzip der Dreieck-Stern-Umwandlung
A
Jede Dreieckschaltung kann in eine elektrisch gleichwertige Sternschaltung umge
wandelt werden.
r12
Die Dreieckschaltung mit den Dreieckwiderständen R1 , R2 und R3 zwischen den Knotenpunkten A, B und C läßt sich in eine elektrisch
gleichwertige Sternschaltung mit den Sternwiderständen r12 , r23 und r31 umwandeln.
R2
R1
r23
r31
S
C
B
Umgekehrt läßt sich die Sternschaltung mit
r12 , r23 und r31 in eine elektrisch gleichwertige
Dreieckschaltung mit R1, R2 und R3 umwandeln
R3
b) Stern-Dreieck-Umwandlung
a) Dreieck-Stern -Umwandlung
l gegeben:
R1
R2
R3
l gegeben:
r12
r23
r31
l gesucht:
r12
r23
r31
l gesucht:
R1
R2
R3
D r e i e c k widerstände :
S t e r n widerstände :
R1 ⋅ R 2
R1 + R 2 + R 3
R1 = r12 + r31 +
r12 ⋅ r31
r23
R2 ⋅ R3
r23 =
R1 + R 2 + R 3
R 2 = r12 + r23 +
r12 ⋅ r23
r31
R 3 ⋅ R1
R1 + R 2 + R 3
R 3 = r31 + r23 +
r31 ⋅ r23
r12
r12 =
r31 =
™
3.
Übungsaufgabe : Brückenschaltung
I3
Berechnen Sie für die nebenstehende Brückenschaltung
a) den Ersatzwiderstand der Schaltung zwischen den
Knotenpunkten A und D ,
b) die Brückenspannung UBC zwischen den Knotenpunkten B und C und schließlich
c) den Brückenstrom I5 sowie alle übrigen Zweigströme.
Lösungen:
RAD = 12,38 Ω
I1 = 5,03 A
I4 = 4,77 A
UBC = –25,8 V
I2 = 3,3 A
I5 = –1,72 A
I3 = 3,04 A
A
I
R3
(25 Ω)
U
(100 V)
I1
U1
U3
(10 Ω)
C
B
I5
R5
I4
R4
R1
(15 Ω)
U2
U4
(5 Ω)
I2
R2
(15 Ω)
D
Lehrgang : ELEKTROTECHNIK 1
Arbeitsblatt Nr. 20 :
Name:
ET1-20-1.DOC - 28.11.02
Netzwerksberechnung mit der Ersatzspannungsquelle
Seite 1
Grundlage der folgenden Darstellung des Ersatzspannungsquellen-Verfahrens ist das im Unterricht behandelte
Einführungsbeispiel (siehe Mitschrift). Dabei wurde angenommen, daß der Widerstand R3 als Lastwiderstand an
einen aktiven Zweipol mit der Spannungsquelle U und den Widerständen R1 und R2 angeschlossen sei.
• Zusammenfassung zur
1.
2.
3.
Bestimmung der Kennwerte U0 und Ri der Ersatzspannungsquelle
Zur Bestimmung der Quellenspannung
U0 der Ersatzspannungsquelle denken wir
uns den Widerstand R3 zunächst herausgetrennt, d.h. es wird angenommen, daß
der aktive Zweipol im Leerlauf betrieben
wird (siehe Bild 1). Die Leerlaufspannung UABo an den Klemmen des
aktiven Zweipols ist dann die Quellenspannung U0 der Ersatzspannungsquelle,
d.h. U0 = UABo (im Leerlauf bei I = 0).
Zur Bestimmung des Innenwiderstandes
Ri der Ersatzspannungsquelle denken wir
uns die Spannungsquelle in Bild 1 kurzgeschlossen (d.h. wir setzen U = 0 !!) und
ermitteln den Ersatzwiderstand RAB des
aktiven Zweipols zwischen den Klemmen A
und B (siehe Bild 2). Dieser Ersatzwiderstand RAB ist dann der Innenwiderstand Ri
der Ersatzspannungsquelle, d.h.: Ri = RAB
(bei U = 0).
Mit der Bestimmung der Kennwerte U0
und Ri der Ersatzspannungsquelle
haben wir für den aktiven Zweipol eine
vereinfachte und elektrisch gleichwertige
Ersatzschaltung gewonnen (siehe Bild 3).
R1
+
U1
A
I=0
I 1o
I
= I 1o
2o
U
U ABo
R2
–
R3
B
Aktiver Zweipol
Bild 1: Aktiver Zweipol im Leerlauf
A
R1
+
U=0!
R3
R2
–
B
Aktiver Zweipol
Bild 2: Aktiver Zweipol mit kurzgeschlossener Spannungsquelle
A
Ri
Ui
+
U
U0
R3
AB
B
Ersatzspannungsquelle
Bild 3: Ersatzspannungsquelle für den aktiven Zweipol
4.
Zur Untersuchung der Schaltung
gemäß der jeweiligen Fragestellung denken
wir uns den Widerstand R3 jetzt an die
Ersatzspannungsquelle (siehe Bild 4)
angeschlossen und bestimmen auf der
Grundlage dieses vereinfachten Ersatzschaltbildes die geforderten Größen, also in
unserem Aufgabenbeispiel den Strom Ι 3
und die Spannung UAB .
A
Ri
Ι3
Ui
+
U0
Ersatzspannungsquelle
U
AB
=U
3
R3
B
Bild 4: Ersatzspannungsquelle mit angeschlossenem Widerstand R3
Lehrgang : ELEKTROTECHNIK 1
Name:
ET1-20-2.DOC - 28.11.02
Netzwerksberechnung mit der Ersatzspannungsquelle
Arbeitsblatt Nr. 20 :
Seite 2
• Aufgabenbeispiel zur Ersatzspannungsquelle
Das Gleichstrom-Netzwerk in Bild 1 soll mit Hilfe des Verfahrens der sog. "Ersatzspannungsquelle" unter
folgenden Gesichtspunkten untersucht werden.
a) Stellen Sie die dem Potentiometer Ra zugeführte Leistung Pa in Abhängigkeit von Ra graphisch in einem
entsprechenden Diagramm dar.
b) Wie groß muß Ra gewählt werden, damit dem Potentiometer die Leistung Pa = 20 W zugeführt wird?
c) Wie groß muß Ra gewählt werden, damit dem Potentiometer die maximale Leistung Pamax zugeführt wird
(Leistungsanpassung). Berechnen Sie diese maximale Leistung Pamax .
100 V
+
R2
C
E
21 Ω
U1
A
Ι AB
R1
12 Ω
+
U AB
Ra
U2
R3
R4
30 Ω
40 Ω
Bild 1 :
Darstellung des Netzwerks als aktiven Zweipol mit den Klemmen A
und B und dem Widerstand Ra als daran angeschlossenen
passiven
Zweipol
B
20 V
R5
Aktiver Zweipol
D
F
50 Ω
• Verfahren zur Bestimmung der Kennwerte U0 und Ri der Ersatzspannungsquelle für den aktiven Zweipol:
ƒ Zur Bestimmung der Quellenspannung U0
der Ersatzspannungsquelle denken wir uns den
Widerstand Ra zunächst herausgetrennt,
d.h. er wird als Ra = ∞ angenommen (Leerlauffall - siehe Bild 2). Die Leerlaufspannung
UABo des aktiven Zweipols ist dann die Quellenspannung U0 der Ersatzspannungsquelle,
d.h. U0 = UABo (bei Ra = ∞).
ƒ Zur Bestimmung des Innenwiderstandes Ri
der Ersatzspannungsquelle denken wir uns
sämtliche Spannungsquellen in Bild 2 kurzgeschlossen (d.h. wir setzen U1 = 0 und
U2 = 0 !!) und ermitteln den Ersatzwiderstand
RAB des aktiven Zweipols zwischen den Klemmen A und B. Der Ersatzwiderstand RAB ist
dann der Innenwiderstand Ri der Ersatzspannungsquelle, d.h.: Ri = RAB (bei U1 = 0
und U2 = 0).
ƒ Zur Untersuchung der Schaltung gemäß der
oben genannten Fragestellungen denken wir
uns den Widerstand Ra an die Ersatzspannungsquelle (siehe Bild 3) angeschlossen
und berechnen auf der Grundlage dieses vereinfachten Ersatzschaltbildes die geforderten
Größen.
100 V
+
R2
C
21 Ω
U1
A
R1
12 Ω
+
U ABo
R345
U2
B
20 V
D
Aktiver Zweipol im Leerlauf
Bild 2 : Vereinfachter aktiver Zweipol im Leerlauf
Ri
A
Ia
U AB
Uo
Ersatz-Spannungsquelle
Ra
B
Bild 3 : Ersatzspannungsquelle für den aktiven Zweipol
Mathematische Begründung der maximalen Leistungsabgabe bei Ra = Ri
• Problemstellung: Auf welchen Wert muß Ra eingestellt werden, damit die Ersatzspannungsquelle an den Außenwiderstand Ra die größtmögliche Leistung abgibt. Dazu müssen wir als erstes eine Gleichung entwickeln, mit der
die Abhängigkeit der Leistung Pa vom Außenwiderstand Ra mathematisch beschrieben werden kann.
Ri
FG
H
= U0 − Ri ⋅
Ua
U0
b
g
Pa = U a ⋅ Ia = U 0 − R i ⋅ Ia ⋅ I a
Ia
Ra
IJ
K
U 0 = const.
R i = const.
U0
U0
⋅
Ri + Ra Ri + Ra
• Daraus ergibt sich für die Abhängigkeit Pa = f (Ra) folgende
Funktionsgleichung
b
Pa = U 0 ⋅ R i + R a
2
g
−1
b
− U0 ⋅ Ri ⋅ Ri + Ra
2
g
−2
• Der Graph dieser Funktionsgleichung ist in dem untenstehenden P-R-Diagramm dargestellt.
• Um nun herauszufinden, bei welchem Ra-Wert die maximale Leistung Pa max auftritt, bilden wir
zunächst die erste Ableitung der Funktion Pa = f (Ra) und gewinnen damit die Steigungsfunktion :
Pa ' =
b gb
g
b gb
eine äußere ,
Ri + Ra
eine innere
Funktion.
g
dPa
−2
−3
= U 02 ⋅ − 1 ⋅ R i + R a ⋅
− U 02 ⋅ R i ⋅ − 2 ⋅ R i + R a ⋅
1
1
1
4
2
4
3
1442443
144
42444
3 14243
dR a
1. Ableitung der äußeren Fkt. 1.Abl. d. inneren Fkt.
Pa ' =
(......)− n ist
b
dPa
= − U 02 ⋅ R i + R a
dR a
g
−2
1.Abl. d. inneren Fkt.
1.Ableitung der äußeren Fkt.
b
+ 2 ⋅ U 02 ⋅ R i ⋅ R i + R a
g
−3
⇐
Steigungsfunktion Pa ' = f ( R a )
• Im Kurvenpunkt des relativen Maximums ist die Steigung des Graphen null (genauer: die Steigung der Tangenten). Daher setzen wir die Steigungungsfunktion Pa' gleich null und lösen dann die Gleichung nach Ra auf.
Pa ' =
dPa
=0
dR a
⇒
b
2⋅ Ri ⋅ Ri + Ra
b
− U 02 ⋅ R i + R a
g = bR + R g
−3
i
−2
a
g
b
g =0
2 ⋅ R ⋅ bR + R g
2⋅ R
=
bR + R g R + R = 1
−2
+ 2 ⋅ U 02 ⋅ R i ⋅ R i + R a
−3
: U 02
2
⇒
i
i
a
i
3
i
i
a
a
2⋅ Ri = Ri + Ra
Ra = Ri
q . e. d
P
Graph der Funktion Pa = f (R a )
7,0
Pa max
W
Tangente
6,0
Pa = f (R a )
5,0
4,0
3,0
2,0
1,0
0
0
2,0
4,0
6,0
8,0
LEISTU~2.DOC - 13.12.02 - Diagramm: P-ANPASS.XLS
10,0
12,0
14,0
16,0
18,0
20,0 Ω
Ra
Lehrgang : ELEKTROTECHNIK 1
Name:
ET1-20-3.DOC - 28.11.02
Netzwerksberechnung mit der Ersatzspannungsquelle
Arbeitsblatt Nr. 20 :
Seite 3
• Übungsaufgaben zur Anwendung der Ersatzspannungsquelle
™
1.
Der nebenstehende aktive Zweipol mit den
Daten U = 4 V , R1 = R3 = 5 Ω und R2 = 6 Ω
wird mit dem Widerstand R4 belastet.
R1
a) Wie groß ist der Widerstand R4 zu wählen,
damit ihm die maximale Leistung zugeführt wird ? [R4 = 3,75 Ω]
U
A
+
R2
b) Wie groß ist diese maximale Leistung ?
[P4max = 150 mW]
R4
R3
B
™
2.
Die nebenstehende Brückenschaltung mit den
Widerständen
A
R1 = R4 = 3 Ω und R2 = R3 = R5 = 6 Ω
R1
R3
I5
liegt an der Spannung U = 12 V.
U
Berechnen Sie mit Hilfe der Ersatzspannungsquelle die Spannung U5 am Widerstand R5 .
U5
+
R5
[U5 = 2,4 V]
R4
R2
B
™
3.
An die Klemmen A und B im Brückenzweig der
nebenstehenden Brückenschaltung ist ein
nichtlinearer Widerstand R5 (VDR-Widerstand)
mit
den unten angegebenen Kennlinienwerten angeschlossen.
I1
R1
Daten der Brückenschaltung:
R1 = 10 Ω
R2 = 270 Ω
R3 = 90 Ω
C
I
U2
U1
A
U
R4 = 30 Ω
I2
B
U
I3
U = 15 V
Bestimmen Sie den Brückenstrom Ι 5 .
R3
R2
I5
R5
U4
U3
[Ι 5 = 145 mA]
D
• Kennlinienwerte des VDR-Widerstandes:
U
3V
4V
5V
6V
7V
8V
9V
10 V
11 V
12 V
Ι
30 mA
50 mA
75 mA
115 mA
155 mA
205 mA
270 mA
340 mA
430 mA
560 mA
I4
R4
Lösung zu Aufgabe 3. von Arbeitsblatt Nr. 20 / Seite 3
1. Schritt :
Berechnung der Quellenspannung Uo (= UqErs.) der Ersatzspannungsquelle
bei offenen Klemmen A und B
C
I 10
I 20
M1
R1
R2
U
A
UABo
B
R4
R3
Berechnung des Innenwiderstandes Ri der Ersatzspannungsquelle
bei kurzgeschlossener Spannungsquelle (d.h. bei U = 0 )
Von den Klemmen A und B aus betrachtet sind bei kurzgeschlossener Spannungsquelle R1 und R3 sowie R2 und R4 parallel und
diese Parallelschaltungen in Reihe geschaltet. Damit gilt:
C
R1
R AB = R13 + R 24
R ⋅R
R ⋅R
R AB = 1 3 + 2 4
R1 + R 3 R 2 + R 4
10 Ω ⋅ 90 Ω
270 Ω ⋅ 30 Ω
R AB =
+
10 Ω + 90 Ω 270 Ω + 30 Ω
R AB = 9 Ω + 27 Ω
R2
U=0
A
B
R4
R3
R AB = R i = 36Ω
D
3. Schritt :
R1 ⋅ I10 + U AB0 − R 2 ⋅ I 20 = 0 (Masche M1)
U AB0 = R 2 ⋅ I 20 − R1 ⋅ I10
U
U
U AB0 = R 2 ⋅
− R1 ⋅
R2 + R4
R1 + R 3
15 V
15 V
U AB0 = 270 Ω ⋅
− 10 Ω ⋅
270 Ω + 30 Ω
10 Ω + 90 Ω
U AB0 = 270 Ω ⋅ 0,05 A − 10 Ω ⋅ 0,15 A
U AB0 = 13,5 V − 1,5 V
U AB0 = U 0 = 12 V
D
2. Schritt :
ET1-20F3.DOC - 01.12.02
Anschluß des nichtlinearen VDR-Widerstandes R5 an die Klemmen A und und B
der Ersatzspannungsquelle und Bestimmung des Arbeitspunktes und damit des
Stromes Ι 5 sowie der Spannung UAB im U-Ι -Diagramm
Ersatz-Spannungsquelle
Ri
I
800
Ι5
A
mA
700
600
U
U AB
Uo
R5
500
400
U0
Ri
B
Koordinatenpunkte der Ri-Geraden:
300
AP
200
Ι5
100
U
U0 = 12 V
und
U 0 12 V
=
= 333,3 mA
Ri
36 Ω
0
0
1
2
3
4
5
6
7
U AB
8
9
10
11
12
U0
13 V
Lehrgang : ELEKTROTECHNIK 1
™
1.
ET1-20-4.DOC - 07.12.02
Netzwerksberechnung mit der Ersatzspannungsquelle
Arbeitsblatt Nr. 20 :
• Weitere
Name:
Seite 4
Übungsaufgaben zur Anwendung der Ersatzspannungsquelle
Bestimmen Sie den Strom Ι F und die Spannung UF an der Diode V1 in dem folgenden Netzwerk.
Ι1
Ι4
Ι
Ι3
Ι2
200
A
ΙF
R1
U1
R2
+
U2
V1
UF
Kennlinie
der Diode V1
150
R3
100
+
B
50
R1 = 100 Ω
U1 = 4,5 V
™
2.
R2 = 100 Ω
U2 = 3,0 V
R3 = 50 Ω
U
[Lösung: ΙF = 40 mA ; UF = 0,86 V]
Zu dem nebenstehenden Netzwerk sind
folgende Berechnungen durchzuführen
a) Welche Leistung nimmt der Widerstand
R6 auf, wenn er auf den Wert 200 Ω
eingestellt worden ist? [P6 = 0,845 W]
+
0
0
R1
R2
100 Ω
100 Ω
U
65 V
b) Wie groß muß der Widerstand R6
gewählt werden, damit ihm die maximal
mögliche Leistung zugeführt wird ?
[R6 = 300 Ω]
0,5
1
1,5
A
Ι6
R5
200 Ω
U6
R3
R4
100 Ω
100 Ω
2V
R6
B
b) Wie groß ist diese maximale Leistung ?
[P6max = 0,88 W]
™
3.
Das im nebenstehenden Schaltplan dargestellte Netzwerk ist unter folgenden Aspekten
zu untersuchen.
R1
[Ri = 3,1 Ω ; U0 = 6,9 V ; P = 3,9 W]
b) Stellen Sie die an den Widerstand R7 abgegebene Leistung in Abhängigkeit von R7
zwischen R7 = 0 Ω und R7 = 10 Ω in einem
Leistungs-Widerstands-Diagramm dar.
R2
3Ω
a) Welche Leistung wird an dem Widerstand
R7 bei Leistungsanpassung abgegeben?
R3
6Ω
Ι3
Ι4
6Ω
U
Ι7
15 V
R4
3Ω
A
R6
R5
6Ω
R7
B
3Ω