Zweipoltheorie, Anwendung

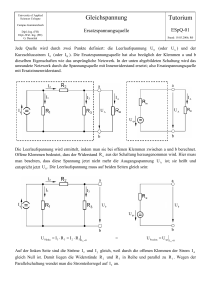
Zweipoltheorie, Anwendung bei der Ersatzspannungsquelle
Die Methode der Ersatzspannungsquelle wird eingesetzt, wenn ein Netzwerk mit Widerständen und
Spannungsquellen vorliegt und beispielsweise nur der Strom durch einen bestimmten Zweig gesucht ist.
Man zerlegt dann die gegebene Schaltung in einen aktiven Zweipol, der die Spannungsquellen enthält
und einen passiven Zweipol, bestehend aus dem interessierenden Zweig.
Sind z.B. Strom Ia und Klemmenspannung Ua eines einzelnen Widerstands Ra gesucht, so trennt man
diesen von der Schaltung und betrachtet den Rest der Schaltung als eine Spannungsquelle mit der
Ersatzquellenspannung Uq=Ul (Leerlaufspannung) und einem inneren Ersatzwiderstand Ri.
Dann fließt durch Ra der Strom Ia=Ul/(Ri+Ra) und der Spannungsabfall am Widerstand Ra ist
Ua= Ia*Ra
Gesucht ist hier im Beispiel Strom und Spannung an R3.
Berechnung des Ersatzwiderstands Ri des aktiven Zweipols: Die idealen Spannungsquellen werden
kurzgeschlossen. Man blickt von außen her auf die Schaltung und berechnet den Ersatzwiderstand
zwischen den freien Klemmen des aktiven Zweipols.
Hier wäre das [R1||(R2 + R4)]= 10||20=20/3Ω
Leerlaufspannung Ul :
Der aktive Zweipol besteht aus der ErsatzSpannungsquelle und einem Ersatz-Innenwiderstand
in Serie.
Ohne äußere Last bedeutet das, dass die ErsatzQuellenspannung gleich der von außen messbaren
Klemmenspannung = Leerlaufspannung sein muss.
Diese ist nun zu berechnen.
Der aktive Zweipol, hier der linke Teil des
Netzwerks wird dazu an den Klemmen
kurzgeschlossen und der Kurzschlussstrom Ik
berechnet:
Hier wäre das Ik = U/R1 = 12V/10Ω =1,2 A
Kurzschlussstrom mal Innenwiderstand ergeben die
Spannung der Ersatzquelle.
Ik*Ri = Uq = 1,2*20/3= 8V
An der offenen Klemme liegt die Leerlaufspannung
Ul = Uq
Der Strom durch den nun wieder angeschlossenen
Außenwiderstand Ra beträgt dann Ia = Uq/(Ri+Ra) =
0,3A, die Spannung Ua = Ia*Ra = 6V
Das war jetzt ein einfaches Beispiel zum besseren Verstehen. Die volle Kraft entwickelt die Methode,
wenn mehrere Spannungsquellen im aktiven Zweipol vorhanden sind.