Wechselstromschaltung - ME-LRT

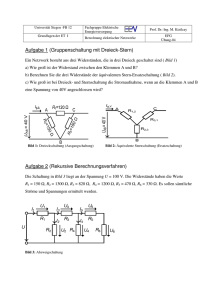
5. Aufgabe
Gegeben ist die untenstehende Wechselspannungsschaltung aus einer idealen
Wechselstromquelle IE mit variabler Kreisfrequenz 2f , 3 Widerständen R, einer
Kapazität C und zwei Induktivitäten L. (Die Klemmen AB sind zunächst
unbeschaltet!)
a.) Berechnen Sie das komplexe Verhältnis ZE (Gesamtwiderstand der Schaltung)!
(Trennen Sie nach Real- und Imaginärteil!)
b.) Bei welcher Frequenz wird das Verhältnis ZE rein imaginär?
c.) Mit welchem Widerstand ZL muß die Schaltung belastet werden, damit in diesem
Lastwiderstand maximale Leistung umgesetzt wird! (Hinweis: Bestimmen Sie hierzu
den Innenwiderstand Zi;AB der Schaltung bezüglich der Klemmen AB!)
Lösung:
a)
ZE ergibt sich aus den einzelnen Widerständen der Schaltung:
Die beiden einzelnen Widerstände R, die obere Spule jL , die Parallelschaltung von
R·jL
1
Widerstand und Spule
und der Kondensator
ergeben folgende
R  jL
jc
Gleichung:
R·jL
1
ZE  R  jL 

R
R  jL jc
Nun wird in der Parallelschaltung der Nenner reell gemacht durch Erweiterung mit
dem konjugiert Komplexen.
R·jL
R·jL(R  jL)
R(L)2  jR 2L


R  jL (R  jL)(R  jL)
R 2  (L) 2
Eingesetzt und nach Real- und Imaginärteil getrennt ergibt sich:

R(L)2
1
R 2L 
ZE  2R  2

j

L




R  (L)2
c R 2  (L)2 

Damit hat ZE einen Realteil von:
und einen Imaginärteil von:
R(L)2
R 2  (L)2
1
R 2L
Im(ZE )  L 
 2
c R  (L)2
Re(ZE )  2R 
b)
Damit ZE rein imaginär wird müsste sich der Realteil zu 0 ergeben. Dies kann aber
über eine kurze Betrachtung ausgeschlossen werden.
Da in dem Bruch nur Quadrate mit Ausnahme des R im Zähler vorhanden sind,
müsste dieses R negativ sein um die 2R, welche vor dem Bruch stehen zu negieren.
Da dann diese aber auch negativ werden ist es nicht möglich diesen Ausdruck im
reellen zu 0 umzustellen und ein komplexes  ist nicht möglich!
c)
Mit dem Wissen, dass ZL  Zi,AB gilt, kann man ZL schnell bestimmen.
Zi,AB  R || jL 
R·jL
R  jL
Dies komplex konjugiert erweitert ergibt:
R·jL R  jL R 2 ·jL  (L) 2
(L) 2
R 2L
Zi,AB 
·



j
R  jL R  jL
R 2  (L)2
R 2  (L) 2
R 2  (L)2
(L)2
R 2L
Zi,AB  2

j
 ZL
R  (L)2
R 2  (L)2