Widerstandsnetzwerk - Carl-Engler

Carl-Engler-Schule Karlsruhe
Laborversuch:
1.
Physik-Labor (BS/BK/FS)
1 (2)
Widerstands-Netzwerk
Grundlagen
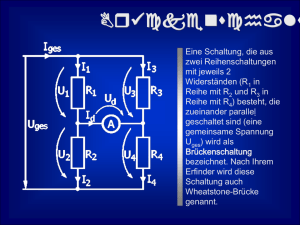
Die Schaltung stellt die Widerstandsanordnung einer Wheatstoneschen Brückenschaltung dar. Die
Wheatstonesche Brückenschaltung ermöglicht die Messung sehr kleiner Widerstandsänderungen. Viele
Sensoren lassen sich nur als Teil einer Brückenschaltung zur Messung physikalischer Grössen einsetzen.
Beispiele sind Dehnungsmeßstreifen (DMS), Feldplatten zur Messung magnetischer Felder oder
Wärmeleitungssensoren als Detektor in einem Gaschromatografen.
Bei kleinen Änderungen des Widerstands der Bauelemente Rb, Rc, Rd und Re ist die Brückenspannung über
dem Widerstand Rf näherungsweise linear. Der Widerstand Rf stellt den Innenwiderstand des Messgerätes
dar, der Widerstand Ra kann als Innenwiderstand der Spannungsquelle betrachtet werden.
Mit der Rechenregeln der Reihen- und Parallelschaltung lassen sich die Werte für die Ströme und
Spannungen nicht berechnen. Mit Hilfe der Kirchhoffschen Regeln lässt sich jedoch ein Lineares
Gleichungssystem aufstellen, aus dessen Lösungen auf die gesuchten Werte zurückgerechnet werden kann.
2.
Vorbereitung
Ohmsches Gesetz
Reihen- und Parallelschaltung
3.
Messen mit dem Multimeter
(Kirchhoffsche Gesetze)
Aufgaben
Es ist eine Schaltung aufzubauen, deren Einzelwiderstände. Teilströme und -spannungen gemessen und mit
den Ergebnissen der Rechnung auf dem Computer verglichen werden sollen.
3.1.1 Auswahl der Bauteile
Wählen Sie sechs Widerstände mit Nennwerten im Bereich zwischen 100 Ohm und 1500 Ohm aus.
Messen Sie mit einem Ohmmeter die genauen Werte der einzelnen Bauteile aus.
3.1.2 Absolute und relative Abweichungen
Geben Sie für alle Widerstände die absoluten und die relativen Abweichungen der gemessenen
Widerstandswerte von den zugehörigen Nennwerten (100%) an.
Geben Sie die Messunsicherheit des Ohmmeters bei der Widerstandmessung an.
widerstandsnetzwerk.odt
Geßler / Müller
Nov 2010
www.ces.karlsruhe.de/culm/
Seite 1 von 2
Carl-Engler-Schule Karlsruhe
Physik-Labor (BS/BK/FS)
2 (2)
3.1.3 Aufbau der Schaltung
Bauen Sie die Schaltung auf dem Experimentierkoffer auf und halten Sie die Anordnung der Bauteile und
ihrer Nennwerte in einem Schaltplan fest.
3.1.4 Messung aller Ströme und Spannungen
Messen Sie mit dem Multimeter alle Bauteilespannungen und alle Bauteileströme, sowie die
Gesamtspannung, den Gesamtstrom und den Gesamtwiderstand. Geben Sie für alle gemessenen Grössen
einen geschätzten Bereich für die Messunsicherheit an.
3.1.5 Simulation auf dem Computer
Starten Sie die angegebene Arbeitsmappe (netzwerk.xls) in der Tabellenkalkulation und berechnen Sie die
zuvor gemessenen Werte. Vergleichen Sie gemessene und berechnete Werte.
3.1.6 Vereinfachte Schaltung
Entfernen Sie den Brücken-Widerstand R f. Messen Sie den Gesamtwiderstand und alle Ströme und
Spannungen. Tragen Sie in der Simulation für R f einen sehr grossen Wert (z.B. 1GΩ) ein. Berechnen Sie
nach den Regeln für Reihen- und Parallelschaltung alle Werte. Vergleichen Sie berechnete, gemessene und
simulierte Werte.
4.
Sonstiges
4.1.1 Messgenauigkeit
Die Messgenauigkeit eines Messgeräts setzt sich zusammen aus der Richtigkeit und der Präzission. Die
Richtigkeit gibt die mögliche Abweichung von einer Messung mit geeichten Messgeräten an. Die Präzission
gibt die möglichen Abweichungen an, die sich bei wiederholter Messung unter den gleichen Bedingungen
(hier: gleiches Bauteil, gleiches Messgerät, gleiche Umgebungsbedingungen ergeben können. Die zum
Messgerät gehörenden Angaben sind auf dem Gerät vermerkt oder dem Handbuch zu entnehmen.
4.1.2 Erläuterungen zum Rechenverfahren
In der Schaltung können drei Maschen festgelegt werden, zu denen jeweils ein Maschenstrom I1, I2, I3
gehört. Die Summe aller Spannungen in einer Masche ergibt Null bzw. die Gesamtspannung. Daher wird für
jede Masche eine Spannungsgleichung aufgestellt.
(Ra+Rb+Rd)*I1
-Rb*I1
-Rd*I1
-Rb*I2
(Rb+Rc+Rf)*I2
-Rf*I2
-Rd*I3
-Rf*I3
(Rd+Re+Rf)*I3
=
=
=
Uges
0
0
Diese drei Gleichungen bilden ein Lineares Gleichungssystem, dessen numerische Lösung durch eine
Funktion in EXCEL bestimmt werden kann. Die Lösung stellt die drei Maschenströme dar.
Die Widerstandsbauteile werden zum Teil von verschiedenen Maschenströmen gleichzeitig durchflossen,
die sich dann addieren bzw. subtrahieren. Aus Strom und Widerstandwert kann die jeweils zugehörige
Spannung berechnet werden.
Bauteileströme
Bauteilespannungen
ia
ib
ic
id
ie
if
ua
ub
uc
ud
ue
uf
=
=
=
=
=
=
I1
I1-I2
I2
I1-I3
I3
I3-I2
=
=
=
=
=
=
ia*Ra
ib*Rb
ic*Rc
id*Rd
ie*Re
if*Rf
Zur Lösung des LGS wird die Matrix invertiert {=MINV()} und mit dem Konstantenvektor multipliziert
{=MMULT()}.
Simulation der Schaltung im Tabellenblatt: netzwerk.xls
widerstandsnetzwerk.odt
Geßler / Müller
Nov 2010
www.ces.karlsruhe.de/culm/
Seite 2 von 2