Grundstromkreis

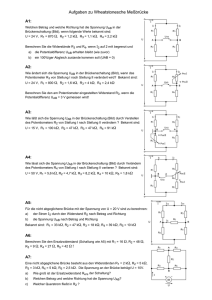
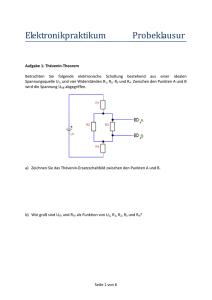
HOCHSCHULE FÜR TECHNIK UND
WIRTSCHAFT DRESDEN (FH)
University of Applied Sciences
Fachbereich Elektrotechnik
Praktikum
Grundlagen der Elektrotechnik
Versuch:
Grundstromkreis
Versuchsanleitung
0.
Allgemeines
Eine sinnvolle Teilnahme am Praktikum ist nur durch eine gute Vorbereitung auf
dem jeweiligen Stoffgebiet möglich. Von den Teilnehmern wird daher eine
intensive Beschäftigung mit der erforderlichen Theorie sowie mit der
Aufgabenstellung bzw. ihrem Zweck vorausgesetzt.
Es gelten die allgemeinen Verhaltensvorschriften der Hochschule, insbesondere
die
 Laborordnung des Fachbereiches Elektrotechnik
und die
 Arbeitsordnung für das Praktikum „Grundlagen der Elektrotechnik“.
06/2014
-1 -
1.
Versuchsziel
Kennen lernen der Strom-Spannungs-Beziehung und der Leistungsverhältnisse
im
Grundstromkreis,
experimentelle
Überprüfung
der
wichtigsten
Berechnungsverfahren linearer Netzwerke.
2.
2.1.
Grundlagen
Grundstromkreis
Der Grundstromkreis ist der einfachste elektrische Stromkreis. Er besteht aus der
Zusammenschaltung eines aktiven Zweipols (Quellspannung Uq und Innenwiderstand Ri) und eines passiven Zweipols (Außenwiderstand Ra). Als
Grundschaltung der Elektrotechnik ist er von allgemeiner Bedeutung, da sich
auch komplizierte Schaltungen auf ihn zurückführen lassen.
U
A
Ui
Ri
Ul = Uq
IAB
UAB
passiver Zweipol
Arbeitspunkt A
UAB
aktiver Zweipol
Ra
Uq
0
B
aktiver Zweipol
IAB
Ik
I
passiver Zweipol
Abb.1 : Schaltbild des Grundstromkreises Abb.2 : U-I-Kennlinie des aktiven
und passiven Zweipols
2.1.1. Strom-Spannungs-Beziehungen
Die Beziehung zwischen Strom und Spannung an den Anschlussklemmen AB des
passiven Zweipols wird durch das Ohmsche Gesetz beschrieben:
U AB =R a  I AB
Für den aktiven Zweipol erhält man aus dem Maschensatz
U AB =U q -R i  I AB
Die grafische Darstellung beider Kennlinien (Abbildung 2) ergibt im
Schnittpunkt den Arbeitspunkt A, dessen Koordinaten den Strom IAB im Kreis
und die Spannung UAB zwischen den Anschlussklemmen beim
Zusammenschalten beider Zweipole angeben.
-2-
Rechnerisch erhält man den Strom IAB und die Spannung UAB im
Grundstromkreis aus dem Ohmschen Gesetz bzw. der Spannungsteiler-Regel:
I AB =
Uq
R ges
U AB =U q 
=
Uq
R i +R a
=I k 
1
R
1+ a
Ri
Ra
1
=U q 
R
R i +R a
1+ i
Ra
Je kleiner Ra wird, desto größer wird der Strom IAB und umso mehr nähert er sich
dem Kurzschlussstrom Ik. Die Spannung UAB hingegen wächst mit zunehmendem
Ra und erreicht bei Ra   die Leerlaufspannung U lAB =U q .
Kurzschluss:
R a =0
U AB =0
I AB =I k =
Leerlauf:
R a =
U AB =U1 =U q
I AB =0
Uq
Ri
2.1.2. Leistungen im Grundstromkreis
Die von der Spannungsquelle Uq abgegebene Gesamtleistung Pges teilt sich auf in
die am Innenwiderstand Ri umgesetzte Verlustleistung Pi und die an den
Außenwiderstand Ra abgegebene Nutzleistung Pa.
Pges =Pi +Pa
Für die Nutzleistung gilt:
Pa  I
2
AB
U 2q  R a
 Ra 
(R i  R a ) 2
Sie ist sowohl für Ra = 0 als auch für Ra =  Null. Dazwischen durchläuft sie ein
Maximum. Durch Differentiation von
findet man für die von einem aktiven
-3-
Zweipol maximal abgebbare Leistung die Bedingung R a =R i . Dieser Sonderfall
heißt Anpassung. Hier beträgt:
Pa =Pa max =
U q2
4  Ri
Der Wirkungsgrad  ist definiert als das Verhältnis der abgegebenen zur
insgesamt aufgewendeten Leistung:
η=
Pa
Ra
=
Pges R i +R a
Folgende charakteristischen Gebiete sind zu unterscheiden:
Kurzschlussgebiet:
R a <<R i
Pa <<Pa max Pi >>Pa
0
Anpassung:
Ra  Ri
Pa  Pa max Pi  Pa
 = 0,5
Leerlaufgebiet:
R a >>R i
Pa <<Pa max Pi <<Pa
1
2.2.
Elektrische Netzwerke
Ein elektrisches Netzwerk entsteht durch Zusammenschalten mehrerer Zweipole.
Es enthält
- Knoten und
- Zweige (aktive und passive Zweipole zwischen zwei benachbarten Knoten).
Als Maschen bezeichnet man die Aneinanderreihung von Zweigen zu
geschlossenen Umläufen.
Grundlage aller Berechnungsmethoden bilden die Kirchhoffschen Sätze:
Knotenpunktsatz:
 I =0
Maschensatz:
 U =0
Für lineare Netzwerke (alle aktiven und passiven Zweipole haben eine lineare UI-Kennlinie) wurden vereinfachte Berechnungsmethoden abgeleitet, z.B. der
Helmholtz’sche Überlagerungssatz und die Zweipoltheorie.
-4-
2.2.1. Berechnung mit Hilfe der Kirchhoffschen Gesetze
Für jedes beliebige Netzwerk mit z Zweigen und k Knotenpunkten liefern die
Kirchhoffschen Gesetze (k-1) Knotenpunktgleichungen und z-(k-1)
Maschengleichungen, die voneinander unabhängig sind. Ersetzt man in den
Maschengleichungen die Spannungen durch die Beziehung U=I  R , so erhält
man ein System von z-Gleichungen, in dem die Zweigströme I die Variablen
sind, und das mit den bekannten Methoden der Determinantenrechnung oder
anderen Verfahren gelöst werden kann.
2.2.2. Berechnung mit Hilfe des Überlagerungssatzes von Helmholtz
In linearen Netzen lässt sich jeder Zweigstrom auffassen als Vorzeichen behaftete
Summe von Teilströmen, wobei jeder Teilstrom von einer Spannungsquelle
angetrieben wird und sich so verhält, als wären alle übrigen Spannungsquellen
unwirksam (gedankliches Kurzschließen der Spannungsquellen, aber nicht der
zugehörigen Innenwiderstände).
2.2.3. Berechnung mit Hilfe der Zweipol-Theorie
(Nur für Studenten mit Elektrotechnik im Hauptfach)
Besteht ein Netzwerk nur aus linearen Elementen, so muss sich auch zwischen
zwei beliebig herausgegriffenen Punkten A und B eine lineare U-I-Beziehung
einstellen. Zur Berechnung eines Zweigstromes kann deshalb der interessierende
Zweig herausgeschnitten, das Restnetzwerk durch einen aktiven Zweipol ersetzt
und die Schaltung damit auf den Grundstromkreis zurückgeführt werden.
Je nach Aufgabenstellung und Art des Netzwerkes kann die Spannungsquellenoder Stromquellenersatzschaltung zur Anwendung kommen:
-5-
SpannungsquellenErsatzschaltung
Schaltbild
StromquellenErsatzschaltung
A
A
Riers
Riers
UAB
Iqers
UAB
Uqers
B
Berechnung der
Ersatzkenngrößen
B
U qers  U lAB
Iqers  I k AB
(Spannung UAB im Netzwerk bei RAB = ,
d.h. Leerlauf)
(Strom IAB im Netzwerk bei
RAB = 0,
d.h. Kurzschluss)
Riers=
an den Klemmen AB hinein gemessener Widerstand (dabei
Quellspannungen gedanklich überbrückt bzw. Stromquellen
unterbrochen)
Anwendungsbereich
3.
Leistungselektronik
Informationstechnik
Vorbereitungsaufgaben
3.1. Für einen aktiven Zweipol werden nacheinander durch Anschluss zweier
verschiedener Widerstände R1 und R2 folgende Wertepaare gemessen:
mit R1:
U1=6,5V
I1=0,5A
mit R2:
U2=3,5V
I2=1,5A
Bestimmen Sie die Widerstände R1 und R2 wie die Kenngrößen Uq, Ik und Ri
des aktiven Zweipols!
-6-
3.2. Stellen Sie graphisch die von obigem aktiven Zweipol abgegebene Leistung
Pa in Abhängigkeit vom Widerstand Ra (Ra=0...15) dar!
3.3. Bestimmen Sie nach dem Helmholz’schen Überlagerungssatz den Strom IAB
in nachstehendem Netzwerk!
U q1 =U q 2 =U q3 =10V
R1 =...=R 8 =2Ω
Uq1
R6
R1
R4
Uq2
R7
R3
A
R5
IAB
R8
4.
R2
Uq3
B
Messaufgaben
A
A
Uq
Uq
V
Ra
V
Ri
Ra
Ri
Schaltung 1
Schaltung 2
4.1. Nehmen Sie nach Schaltung 1 die Strom-Spannungs-Kennlinie des aktiven
Zweipols auf und bestimmen Sie aus dieser die Kenngrößen Uq, Ik und Ri.
-7-
4.2. Messen Sie nach Schaltung 2 I und U in Abhängigkeit vom Widerstand Ra
und stellen Sie die Kennlinien in normierter Form
R
U
I
und =f( a )
Ul
Ik
Ri
sowohl mit linearem als auch mit einfach-logarithmischem (Ordinate linear
dargestellt) Achsenmaßstab dar!
[Wählen Sie Ra = (0,125; 0,25; 0,5; 1; 2; 4; 8; 16)  Ri!]
4.3. Berechnen Sie aus den Messwerten für I, U, Ik und Ul die normierten
Leistungskurven (bezogen auf die Leistung Pk =I 2k  R i ):
Pa
Pi
;
;
Pk
Pk
Pges
Pk
und  in Abhängigkeit von
Ra
Ri
und stellen Sie diese graphisch dar.
Welche maximale Leistung kann der untersuchte aktive Zweipol abgeben?
4.4. Zeichnen Sie das Schaltbild des Netzwerkes am Versuchsplatz ab! Messen
Sie mit dem Digitalmultimeter die Einzelwiderstände des Netzwerkes und
den Ersatzinnenwiderstand Riers bei überbrückten Quellspannungen!
Kontrollieren Sie den gemessenen Riers durch Berechnung aus den
Einzelwiderständen!
4.5. Messen Sie die Quellspannungen Uq aller Spannungsquellen und die
Leerlaufspannung U lAB des Netzwerkes!
Berechnen Sie nach dem Überlagerungssatz den Zweigstrom IAB im
untersuchten Netzwerk!
4.6. Überprüfen Sie die Anwendbarkeit des Überlagerungssatzes durch Messung
der von den einzelnen Quellspannungen Uq hervorgerufenen
Teilzweigströme I AB ν und des Gesamtzweigstromes IAB!
Vergleichen Sie die Messergebnisse für die Teilzweigströme und den
Gesamtzweigstrom mit den in 4.5. errechneten Werten!
-8-