Seiten 16 bis 20

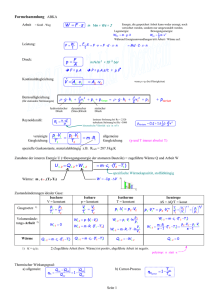
Worte
Werke
Werte
BBS Idar-Oberstein
Name:
2.4.1 Der erste Hauptsatz der Wärmelehre
In einem abgeschlossenen System, in dem beliebige
Vorgänge
ablaufen,
bleibt
die
vorhandene
Gesamtenergie unverändert. Energie kann weder
verloren gehen, noch aus dem Nichts entstehen.
Anders formuliert:
Es ist unmöglich, ein Perpetuum mobile zu
konstruieren.
Perpetuum mobile (lateinisch: das sich ewig Bewegende),
System, das, einmal in Bewegung gesetzt, ohne weitere
Energiezufuhr auf Dauer in Bewegung bleibt und so
unendlich viel Arbeit verrichten kann.
Die Einheit der Wärme ist (wie die Arbeit und Energie)
Nm, Ws oder J.
Später werden wir noch sehen (s. 2.6), dass die
Speicherform von Wärme „innere Energie“ genannt wird
und dass sie nicht so problemlos wie andere
Energieformen umgewandelt werden kann. ( 2. Hauptsatz, s. 2.6) (So warten die „Jungs vom Patentamt“ immer
noch vergeblich auf den Trick, mit dem man z.B. die
Energie von erhitzten Kfz-Bremsscheiben wieder zum
Antreiben des Fahrzeuges nutzen könnte.)
Wie groß ist die zum Erhitzen von Stoffen
notwendige Wärme?
2.4.2 Die spezifische Wärmekapazität
Die erforderliche Wärme zum Erhitzen eines Stoffes
steigt
• proportional zur Masse und
• (annähernd) proportional zur Temperaturerhöhung und
• ist abhängig von der jeweiligen Art des Stoffes
Q ~ m⋅ ϑ
Durch Einführung eines (stoffabhängigen)
Proportionalitätsfaktors, der Zahlen und
Einheiten anpasst, wird aus der Proportion
eine Gleichung:.
Wärmedifferenz zum
Erhitzen eines Stoffes
Die spezifische Wärmekapazität c eines Stoffes
gibt an, wie viel Wärme notwendig ist, um 1 kg
eines bestimmten Stoffes um 1 K zu erhitzen.
Q = c⋅m⋅
ϑ
Technik 13:
Thermodynamik/Strömungsmechanik
Datum:
(Sie ist temperaturabhängig.) Ihre Einheit ist kJ⋅kg-1⋅K-1
Spezifische Wärmekapazitäten zwischen 0 oC
und 100 oC in kJ/(kg⋅K)
Wasser
4,19
Aluminium 0,88
Öl
1,9 bis 2,1
Stahl
0,45 - 0,68
Quecksilber 0,139
Blei
0,125
Mauerwerk 0,8 bis 2,0
Glas
0,8
Seite
16
Bei den Änderungen von Druck, Temperatur und
Volumen eines Gases wird immer Wärme und/oder Arbeit
zu- oder abgeführt. Welchen Zusammenhang gibt es
zwischen diesen Größen?
2.5 Energieaustausch
Die spez. Wärmekapazität eines Gases ist ebenfalls
stoffabhängig und hängt stark von der Art der
Zustandsänderung ab:
2.4.3 Die spezifische Wärmekapazität von Gasen
Erhitzt man z.B. Luft laut
Skizze isochor, so ist die
erforderliche Wärme und
somit c kleiner als bei
isobarer Erwärmung.
cv ist kleiner als cp , denn
bei der isobaren Zustands-
Um den Zustand eines Gases zu ändern, muss ein
Energietransport (über die Systemgrenzen hinein oder
heraus) stattfinden. Dies kann nur durch die Energietransportformen Arbeit und/oder Wärme geschehen.
(Wärme und Arbeit sind also keine Zustands-, sondern
Prozessgrößen.)
a) Die Wärme Q ist eine Energieform, die allein auf
Grund von unterschiedlichen Temperaturen übertragen wird.
b) Die Arbeit W (=Kraft * Weg) geschieht durch die
Volumenänderung des Gases mittels Kraftanwendung.
z.B. bei konstantem Druck
bei beliebigem Druckverlauf
änderung dehnt sich das Gas aus und wird so noch zusätzlich Arbeit verrichtet.
Spezifische Wärmekapazitäten cv und cp in kJ/(kg⋅K)
Argon Ar
Helium He
Luft
Sauerstoff O2
Stickstoff N2
Wasserstoff H2
Kohlendioxid CO2
Methan
CH4
cp in
cv in
kJ/(kg⋅K)
kJ/(kg⋅K)
0,523
5,234
1,004
0,917
1,038
14,319
0,837
2,219
0,318
3,211
0,716
0,657
0,741
10,157
0,649
1,696
κ = c /c
p
v
(vgl. 2.5.4)
1,66
1,66
1,402
1,399
1,400
1,402
1,299
1,319
Minus-Zeichen kennzeichnet die Richtung:
Arbeit geht hinaus (-) oder hinein (+)
Die Zuführung von Arbeit oder/und Wärme in ein abgeschlossenes Gas erhöht (lt. 1. Hauptsatz) die Energie des
Systems.
Worte
Werke
Werte
BBS Idar-Oberstein
Name:
Technik 13:
Wie aber kann in einem Gas überhaupt Energie
gespeichert werden; es wirken doch zwischen den Gasmolekülen überhaupt keine (elektrostatischen, magnetischen oder sonstige Spann-)Kräfte?
(Die chemischen Bindungskräfte und die Atomkernbindungsenergien
ignorieren wir, da sich diese in thermodynamischen Prozessen ja eh
nicht verändern.)
Die zugeführten Energien können also einzig und allein
nur als Bewegungsenergie der Moleküle gespeichert sein.
Diese Speicherform der Energie nennt man:
Die innere Energie U ist die Energie, die ein Stoff auf
Grund seiner Molekularbewegungen hat. Sie äußert sich
nach außen über die Temperatur bzw. den Aggregatzustand ( vgl. 2.?.?). U ist Null bei 0 K. Sie ist eine
Zustandsgröße.
Am einfachsten berechnet man die innere Energie eines
bestimmten Zustandes mit der Wärmemenge, die man zur
isochoren Änderung benötigt. (denn dann ist keine Arbeit
mit im Spiel; vgl.2.4.3) U = Q1-2 + W1-2
= m⋅⋅cv⋅ (T2-T1)
Die Formel zeigt, dass sowohl durch Wärmezufuhr als
auch durch Arbeitszufuhr die innere Energie steigt. (vgl.
1. Hauptsatz, 2.4.1) Arbeit und Wärme sind math. positiv,
wenn sie die innere Energie erhöhen; sie sind negativ,
wenn sie abgeführt werden Z.B.: in einem
Verbrennungsmotor wird Wärme zugeführt (+Q) und
Arbeit abgeführt (-W).
Laien, zu denen wir schon lange nicht mehr zählen, unterscheiden
nicht zwischen der Energietransportform Wärme und der
Energiespeicherform innere Energie. Das ist auch beim
Betrachten von festen und flüssigen Stoffen nicht weiter
tragisch, da die zugeführte Wärme Q dort auch irgendwann immer 100%ig wieder als Wärme heraus kommt;
ganz anders ist es bei Gasen!!! (wie z.B. bei Verbrennungsmotoren)
Thermodynamik/Strömungsmechanik
2.5.1 Energieaustausch bei der Isochoren
Wie oben schon beschrieben, wird
beim Überführen des Gases vom
Zustand 1 nach Zustand 2 keine Arbeit
verrichtet. ∆U = Q1-2 + W1-2 Somit
kommt es zu einer vollständigen
Umwandlung von Wärme in innere Energie. ∆U = Q1-2
W1-2 = 0
Q1-2 = m⋅cv⋅T2-T1)
Isochore
2.5.2 Energieaustausch bei der Isobaren
Die Arbeit W1-2 = -p⋅∆V = p⋅ (V1-V2);
Sie ist laut Definition negativ, wenn das
Gas expandiert und somit Arbeit
abgeführt wird.
p⋅V1 ist laut Gasgesetz m⋅Ri⋅T1 ; also kann man die Arbeit
auch aus m⋅Ri⋅ (T1-T2) berechnen.
W1-2 = p⋅ (V1-V2)
W1-2 = m⋅Ri⋅ (T1-T2)
Q1-2 = m⋅cp⋅ (T2-T1)
Isobare
Seite
17
Schauen wir uns die 2. Energietransportform an: Wird bei
der isothermen Zustandsänderung Wärme zu- oder
abgeführt? Klein Fritzchen würde vorschnell sagen:
„Nein, denn die Temperatur bleibt doch konstant.“
FALSCH, wenn die Temperatur konstant bleibt, dann
bleibt die innere Energie konstant.
∆U = m⋅cv⋅ (T2-T1) = Q1-2 + W1-2 .= 0
D. h. die durch die Verdichtungsarbeit W1-2 im obigen
Beispiel zugeführte Energie, muss, damit U und T nicht
ansteigen, sofort wieder in Form von Wärme abgeführt
werden!!! ∆U = Q1-2 + W1-2 .= 0 Q1-2 = -W1-2 .
W1-2 = p1⋅V1⋅ ln(V1/V2)
Q1-2 = -W1-2
Isotherme
W1-2 = m⋅Ri⋅T ⋅ ln(V1/V2)
Damit ein isothermer Prozess stattfinden kann, muss man
während des Verdichtens das Gas kühlen (bzw. beim
Expandieren das Gas erhitzen) oder den Prozess ganz,
ganz langsam ablaufen lassen, damit die Umgebung für
Temperaturausgleich sorgen kann.
Was aber passiert, wenn der Prozess sehr schnell abläuft
und/oder das Gas gut isoliert ist?
2.5.4 Energieaustausch bei der Isentropen
Isentrop = bei gleichbleibender Entropie
verlaufend; entspricht: „adiabatisch“ = gr.
undurchlässig (für die Wärme)
Entropie S =Maß für den Ordnungszustand eines
thermodynamischen Systems, kennzeichnet
den Verlauf eines Wärmeprozesses
vgl. 2.6 ∆S=∆Q/T
2.5.3 Energieaustausch bei der Isothermen
Die (Volumenänderungs-)Arbeit ist
hier schwieriger zu bestimmen, da sich
die Kraft längs des Weges ändert. Die
Arbeit ist die Summe aller Flächenelemente unter der p-V-Linie:
wird für unendlich kleine (u. somit math.
genaue) Flächenelemente zu Integral von - pi ⋅ dV.
Wie wir aus Mathe 12 wissen, ist
Datum:
. Somit ist
Für m⋅R⋅T kann man laut allg. Gasgesetz auch p⋅V einsetzen.
Wenn beim Verdichten keine Wärme
abgeführt wird, so steigt die innere
Energie und somit die Temperatur an.
Deshalb verläuft (laut Gasgleichung)
die Zustandslinie im p-V-Diagramm steiler als die der
Isothermen.
Wenn Q=0, dann folgt aus der allg. Gleichung
∆U = Q1-2 + W1-2 = m⋅cv⋅ (T2-T1).
∆U = W1-2 = m⋅cv⋅ (T2-T1)
Worte
Werke
Werte
BBS Idar-Oberstein
Name:
Technik 13:
Schlussbetrachtung:
Ein isentroper (bzw. adiabatischer) Prozess ist ein
Vorgang, bei dem Temperatur, Druck und Volumen
verändert werden, ohne dass mit der Umgebung Wärme
ausgetauscht wird. Ein alltägliches Beispiel ist das
Versprühen eines Sprays aus einer Dose, deren
Temperatur dabei absinkt: Wenn sich Gase ausdehnen
(hier das Treibgas des Sprays), dann wird Energie
„verbraucht“ und sie wird dem „Wärmeinhalt“ der
Flüssigkeit in der Dose entzogen. Der Vorgang läuft zu
schnell ab, als dass der Wärmeverlust durch die
Umgebung ausgeglichen werden könnte, daher das
Absinken der Dosentemperatur. Den umgekehrten
Effekt eines Temperaturanstiegs stellt man fest, wenn
ein Gas sehr schnell komprimiert wird (z.B. beim
Reifenaufpumpen mit der Luftpumpe). Zahlreiche
alltägliche Systeme, z.B. die Motoren von Autos, nutzen
adiabatische Prozesse.
Somit kennen wir alle Energieformen der Isentrope;
jedoch ihren p-V-Verlauf kennen wir noch nicht. Wir
wissen nur, dass er steiler als der der Isothermen ist. Wie
der Druck vom Volumen abhängt, müssen wir doch wohl
nicht induktiv (mittels Versuche) bestimmen, sondern wir
können ihn mathematisch herleiten
Die gesuchte Funktion p(V) muss 1. dem allg. Gasgesetz
p⋅V=m⋅Ri⋅T und 2. der Bedingung ∆U=W1-2 .
entsprechen:
Ri⋅p⋅dV = cv⋅p⋅dV + cv⋅V⋅dp
cv⋅V⋅dp + (Ri+ cv)p⋅dV =0
Da cv + Ri = cp = und κ = cp/cv ist, folgt:
V⋅dp + κ⋅p⋅dV =0 bzw .
dp/p = κ⋅dV/V
κ
Durch Integration erhält man p⋅V = konst.
Ist jedoch einer der beiden Größen nicht gegeben, kann
man die Formel mittels allg. Gasgleichung passend
umformen. (vgl. untere Tabelle!) (κ-Werte: Seite16)
Im Folgenden wollen wir unsere Kenntnisse der Thermodynamik für technische Prozesse, z.B. für Verbrennungsmotoren, ausnützen:
„Wie können wir aus Wärme (bei möglichst hohem
Wirkungsgrad) Arbeit erhalten?“
Noch einmal alle wichtigen Sonderfälle im Überblick:
Isochore
V = konstant
Gasgesetze
Isobare
p = konstant
Isotherme
T = konstant
Datum:
W1-2 = 0
Wärme
Q1-2 = m⋅cv⋅ (T2-T1)
Isentrope
S = Q/T = konst
κ = cp/cv
W1-2 = m⋅Ri⋅ (T1-T2)
Q1-2 = m⋅cp⋅ (T2-T1)
Q1-2 = - W1-2
2) zugeführte Arbeit (bzw. Wärme) ist positiv, abgeführte Arbeit ist negativ
18
Der erste Hauptsatz beschreibt nur eine Energiebilanz,
erfasst aber damit die Vorgänge nicht vollständig. Wasser
z.B., das einen Felsen herab stürzt, erwärmt sich. Aber
laut erstem Hauptsatz wäre auch das Umgekehrte
möglich! ! Ich hab’ aber noch nie Wasser den Berg
hinauf laufen ‘sehen, das sich dabei auch noch in
Übereinstimmung mit dem Energieerhaltungssatz
abkühlte.
Wir müssen also die Richtung eines Prozesses beachten.
In der Mechanik gibt es viele Vorgänge, die umkehrbar
(=reversibel) sind (sofern man von der unvermeidlichen
Reibung absieht):
• z.B. die kinetische Energie eines Balls wandelt sich in
Spannenergie und wieder umgekehrt.
• z.B. mech. oder el. Schwingungsvorgänge bauen auf
diesem Energieaustausch auf.
• z.B. ist auch folgender Gedankenversuch zum Spannen einer
Feder durch ein Gewicht zu jedem
Zeitpunkt umkehrbar
W1-2 = m⋅cv⋅ (T2-T1)
W1-2 = p(V1-V2)
Seite
2.6 Zweiter Hauptsatz der Wärmelehre
1)
Volumenänderungs-Arbeit 2)
1)
Thermodynamik/Strömungsmechanik
Q1-2 = 0
Worte
Werke
Werte
BBS Idar-Oberstein
Name:
Bei thermischen Prozessen sieht das aber ganz anders aus:
.
2.6.1 Reversible und irreversible Vorgänge
Beobachtungen bestätigen, dass natürliche Vorgänge
immer nur in eine Richtung ablaufen. Berühren sich z.B.
zwei Körper verschiedener Temperatur, so stellt sich nach
einiger Zeit eine Mischungstemperatur ein, niemals ist
aber das Erwärmen eines Körpers auf Kosten des anderen
möglich. Wärme kann immer nur vom wärmeren
Körper zum kälteren fließen.
Diese Tatsache kann man (vgl. kin. Gastheorie) statistisch
deuten.
Gedankenexperiment:
Ein eingeschlossenes Gas kann
durch einen Spalt in den 2. Raum
strömen. (Die kin. Energie der
Moleküle bleibt dabei unverändert.)
Die Wahrscheinlichkeit, dass sich irgendwann der
ursprüngliche Zustand 1 wieder einstellt, ist Null.
Hausaufgaben: ;-)
1. Schütteln Sie ein Glas mit 100 roten und 100 blauen
Kugeln (alle Kugeln seien gleich groß) so lange, bis
alle roten Kugeln oben und alle blauen Kugeln unten
liegen.!? oder
2. Entwerfen Sie einen Schiffsmotor, der den Wärmeinhalt des Meerwassers ausnützt. Die Maschine nimmt
Wasser auf und gibt es als Eiswürfel wieder frei.
oder
3. Akzeptieren Sie folgendes Naturgesetz ...
Der zweite Hauptsatz der Wärmelehre:
Es ist unmöglich, ein Perpetuum mobile zweiter Art
zu konstruieren.
anders ausgedrückt:
Es gibt keinen Vorgang, der nichts weiter bewirkt,
als Arbeitsverrichtung durch die Abkühlung eines
„Wärme“reservoirs .
oder vielleicht so:
Jeder physikalische Vorgang verläuft in der
Richtung, dass der Endzustand wahrscheinlicher ist
als der Anfangszustand.
Technik 13:
Thermodynamik/Strömungsmechanik
Einen Sonderfall (und Idealfall) stellt die Isentrope dar.
Wenn bei diesem Prozess keine (Reibungs-)Verluste auftreten, wird keine Wärme zugeführt: der Vorgang ist
reversibel.
Physiker benutzen das Verhältnis von zugeführter Wärme zur jew.
absoluten Temperatur als Maß für diese Irreversiblität und nennen sie
Entropie (∆S=∆Q/T). Wir rechnen nicht damit
Einen zweiten Hauptsatz hab’ ich noch ..
In einem abgeschlossenen System kann die Entropie nur
zunehmen.
(... ‘drum ereilt die Welt eines Tag’s den Wärmetod.)
.
.
Wenn wir nun also eine Wärmekraftmaschine (=
Maschine, die aus Wärme möglichst viel Arbeit
„erzeugt“) konstruieren wollen, dann muss die Wärme auf
höherem Temperaturniveau als die Umgebungstemperatur
zugeführt werden.
Welche Prozesse müssen in einer Wärmekraftmaschine
ablaufen?
2.6.2 Kreisprozesse
Die ersten Wärmekraftmaschinen arbeiteten mit einem
atmosphärischen Gas (bzw. Dampf von 1 bar), dem
zwangsläufig nur auf sehr niedrigem Temperatur-Niveau
Wärme zugeführt wurde; der Wirkungsgrad war deshalb
sehr gering.
Da die Maschinen periodisch arbeiten, muss das Gas bei
jedem Durchlauf wieder in den alten Zustand
zurückgeführt werden, bzw. durch neues ausgetauscht
werden. Deshalb spricht man von einem Kreisprozess.
Deutlich wird dies z.B. in einem p-V-Diagramm:
• Damit Arbeit verrichtet wird, muss der Rücklauf unter
einem geringeren Druck erfolgen als der Arbeitshub.
• Damit die Wärme auf einem hohen Niveau zugeführt
werden kann, verdichtet man zuerst das Gas. (Man
steckt also zuerst Arbeit hinein, bevor man Arbeit
herausbekommt.)
Datum:
Seite
19
Die Kompressionsarbeit ist kleiner als die Expansionsarbeit (bei linksläufigen Prozessen umgekehrt). Da es
aber nach dem 2. Hauptsatz nicht möglich ist, den Anfangszustand des Gases ohne Eingriff von außen zu erreichen, muss gekühlt werden.
│Qzu│-│Qab│ = │W│
( korrekt: Qzu + Qab = -W )
negativ
Wärme kann also nie vollständig in Arbeit überführt
werden.
Auch das ist eine Konsequenz des 2. Hauptsatzes.
Wie kann man die Güte des Kreisprozesses beschreiben?
2.6.2.1 Thermischer Wirkungsgrad
Unter dem Wirkungsgrad versteht man (in der Technik)
immer das Verhältnis von ... .
nutzbare Energie =
„Exergie“
Qab = „Anergie“ geht
„verloren“
Der thermische Wirkungsgrad ist somit definiert als:
Zusätzliche mechanische (Reibungs-)Verluste der
Kraftmaschine werden gesondert verrechnet und mit dem
thermischen Wirkungsgrad zum Gesamtwirkungsgrad
multipliziert. Wir können dies vernachlässigen.
Wie kann man einen rel. hohen thermischen Wirkungsgrad erreichen?
2.6.2.2 Carnot-Prozess
Carnot, Nicolas Léonard Sadi (1796-1832), französischer
Physiker und Ingenieur, entdeckte, dass Wärme nicht von einem
kälteren zu einem wärmeren Körper übergehen kann und dass
der Wirkungsgrad einer Maschine davon abhängig ist.
Carnot entwarf einen Kreisprozess, der den bestmöglichen Wirkungsgrad liefert: Die Wärme aus einem
Energiereservoir wird bei höchster Temperatur zugeführt
und die für den Kreisprozess unvermeidliche Abkühlung
Worte
Werke
Werte
BBS Idar-Oberstein
Name:
Technik 13:
Thermodynamik/Strömungsmechanik
sollte bei der tiefstmöglichen Temperatur, der
Umgebungstemperatur erfolgen. Wärmezu- und
-abfuhr erfolgen demnach isotherm. Um auf die jew.
Temperaturniveaus zu gelangen, verwendet er die
isentrope (Q=0) Kompression und die isentrope
Expansion.
Datum:
Seite
20
2.6.2.3 Realer Prozess am Beispiel des Otto-Motors
In der folgenden Skizze ist die prinzipielle Arbeitsweise
eines Otto-Motors dargestellt.
Abgase der Gasturbine erhält das
konventionelle Wärmekraftwerk zum
„Nulltarif“
Carnot-Prozess ist in der Realität nicht
durchführbar.
Carnot-Prozess
Kein anderer Kreisprozess kann die Wärme besser
ausnützen.
Der Carnot-Prozess dient als Orientierung für alle
möglichen thermischen Kreisprozesse. Er verdeutlicht die
max. erreichbare Energieausbeute und zeigt, dass sich der
thermische Wirkungsgrad mit steigender Temperatur
verbessert. Jedoch sind einer Erhöhung der
Prozesstemperaturen u.a. durch die begrenzte Werkstofffestigkeit Grenzen gesetzt.
Reale Kreisprozesse arbeiten mit einem schlechteren
Wirkungsgrad u.a., weil ihre Abgastemperaturen prozessbedingt rel. hoch sind.
Verdichtungs- und Arbeitstakt setzen sich (theoretisch)
aus Isentropen, und Isochoren zusammen. Jedoch die
wirklich im Zylinder gemessenen Werte weichen etwas
davon ab: Indikatordiagramm