Formelsammlung

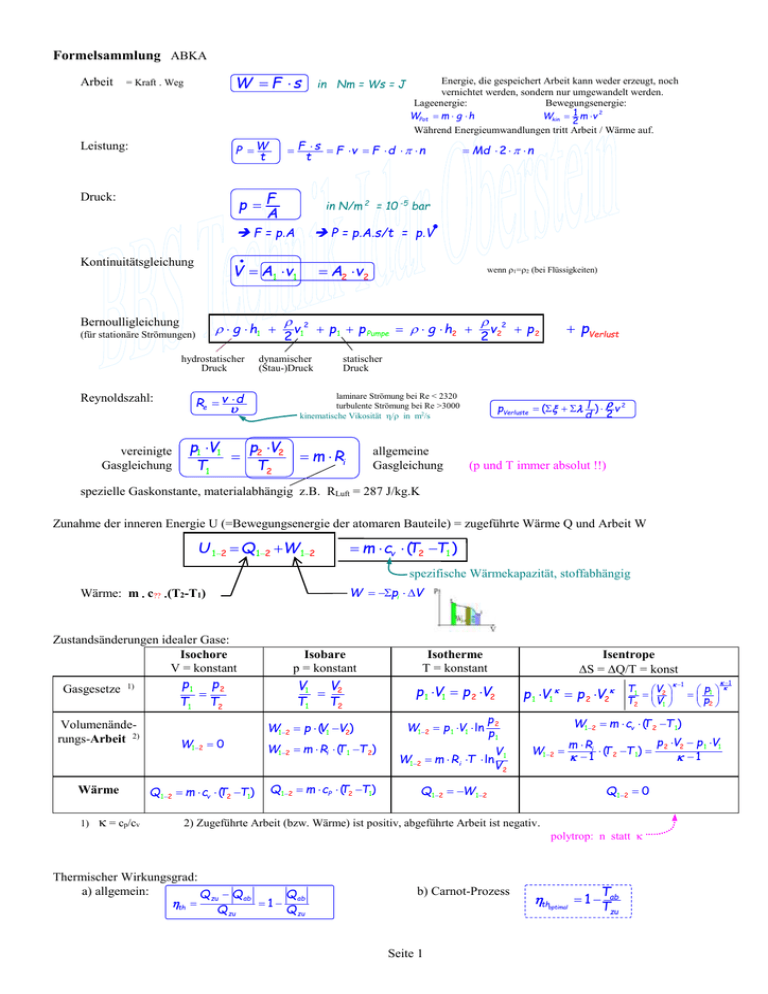
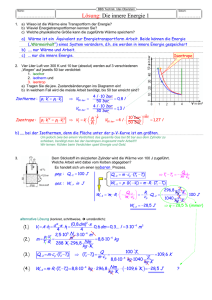
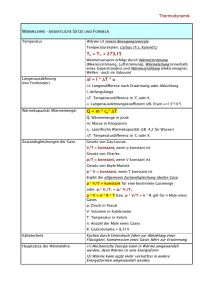
Formelsammlung ABKA
Arbeit
W  F s
= Kraft  Weg
P W
t
Druck:
pF
A

  g  h1 
(für stationäre Strömungen)
hydrostatischer
Druck
vereinigte
Gasgleichung
 P = pAs/t = pV
V  A1 v1
Bernoulligleichung

2
 A2 v2
wenn 1=2 (bei Flüssigkeiten)
v12  p 1  p Pumpe    g  h2 
dynamischer
(Stau-)Druck
Re  v  d
 Md  2    n
in N/m 2 = 10 -5 bar
 F = pA
Kontinuitätsgleichung
Energie, die gespeichert Arbeit kann weder erzeugt, noch
vernichtet werden, sondern nur umgewandelt werden.
Lageenergie:
Bewegungsenergie:
Wkin  1 m v 2
WPot  m  g  h
2
Während Energieumwandlungen tritt Arbeit / Wärme auf.
 F  s  F v  F  d    n
t
Leistung:
Reynoldszahl:
in Nm = Ws = J

2
statischer
Druck
laminare Strömung bei Re < 2320
turbulente Strömung bei Re >3000
kinematische Vikosität / in m2/s

p1 V1
p V
 2 2
T1
T2
 pVerlust
v22  p 2
 m  Ri
allgemeine
Gasgleichung

pVerluste  (   l )  v 2
d 2
(p und T immer absolut !!)
spezielle Gaskonstante, materialabhängig z.B. RLuft = 287 J/kgK
Zunahme der inneren Energie U (=Bewegungsenergie der atomaren Bauteile) = zugeführte Wärme Q und Arbeit W
U 12  Q 12 W 12
 m  cv  (T2 T1 )
spezifische Wärmekapazität, stoffabhängig
W  pi  V
Wärme: m  c?? (T2-T1)
Zustandsänderungen idealer Gase:
Isochore
V = konstant
p1 p2
Gasgesetze 1)

T1 T2
Volumenänderungs-Arbeit 2)
Wärme
1)
 = cp/cv
Isobare
p = konstant
V1
V
 2
T1
T2
W12  p  (V1 V2)
Isotherme
T = konstant
p 1 V1  p 2 V2
W12  p 1 V1  ln
Isentrope
S = Q/T = konst
p 1 V1   p 2 V2
p2
p1
W12  0
W12  m  Ri  (T 1 T 2)
V
W12  m  R i T  ln 1
V2
Q12  m  cv  (T2 T1)
Q12  m  cP  (T2 T1)
Q12  W12
W12 
Q zu
Q zu
Q12  0
th
optimal
Seite 1
 1

p V  p 1 V1
m  Ri
 (T T )  2 2
 1 2 1
 1
polytrop: n statt 
b) Carnot-Prozess
p
  1 
 p2 
W12  m  cv  (T 2 T 1)
2) Zugeführte Arbeit (bzw. Wärme) ist positiv, abgeführte Arbeit ist negativ.
Thermischer Wirkungsgrad:
a) allgemein:
Q zu  Q ab
Q ab
th 
1
 1
T1 V2 

T2 V1 
T
 1  ab
Tzu