Häufigkeitsverteilungen beschreiben File

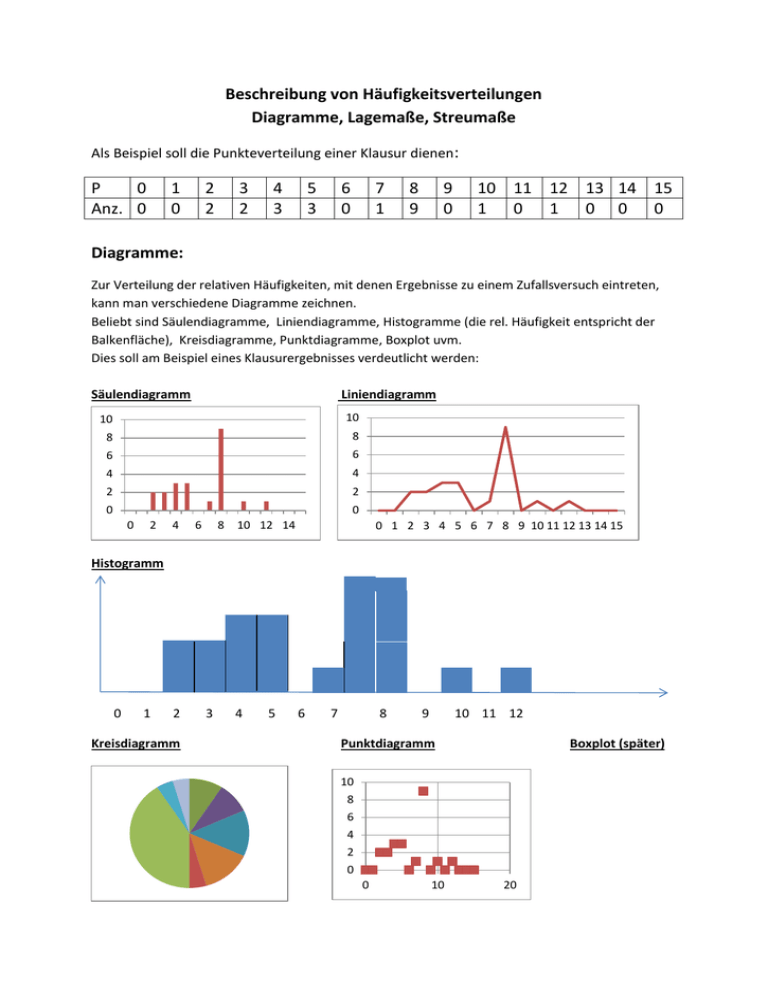
Beschreibung von Häufigkeitsverteilungen
Diagramme, Lagemaße, Streumaße
Als Beispiel soll die Punkteverteilung einer Klausur dienen:
P
0
Anz. 0
1
0
2
2
3
2
4
3
5
3
6
0
7
1
8
9
9
0
10 11 12 13 14 15
1 0 1 0 0 0
Diagramme:
Zur Verteilung der relativen Häufigkeiten, mit denen Ergebnisse zu einem Zufallsversuch eintreten,
kann man verschiedene Diagramme zeichnen.
Beliebt sind Säulendiagramme, Liniendiagramme, Histogramme (die rel. Häufigkeit entspricht der
Balkenfläche), Kreisdiagramme, Punktdiagramme, Boxplot uvm.
Dies soll am Beispiel eines Klausurergebnisses verdeutlicht werden:
Säulendiagramm
Liniendiagramm
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
8
10 12 14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Histogramm
0
1
2
Kreisdiagramm
3
4
5
6
7
8
9
10 11 12
Punktdiagramm
Boxplot (später)
10
8
6
4
2
0
0
10
20
Lagemaße
Arithmetisches Mittel = Durchschnittswert:
Das arithmetische Mittel x ergibt sich als Summe der gemessenen Werte multipliziert mit
n
deren relativen Häufigkeit:
x =
x r
i 1
i i
n = Anzahl der Messwerte, xi = i. Messwert, ri = rel. Häufigkeit des i. Messwertes.
Beispiel : x  2 
2
2
3
3
1
9
1
1
 3   4   5   7   8   10   12  = 6,27 n = 8
22
22
22
22
22
22
22
22
Modus:
Der Modus ist der am häufigsten vorkommende Messwert. Er ist unter Umständen nicht
eindeutig.
Beispiel: Modus 8
Quantile:
Quantile Qp teilen die Messwerte in Bereiche ein.
Man stellt sich die gemessenen Werte der Reihe und Häufigkeit nach geordnet vor.
Beispiel: 2 2 3 3 4 4 4 5 5 5 7 8 8 8 8 8 8 8 8 8 10 12
Das Quantil Qp teilt diese Reihe im Verhältnis p zu (1-p), d. h. es gilt:
0,5 (xnp + xnp+1) für np natürlich
Qp =
xnp 1 für np nicht natürlich
Mindestens np Werte sind kleiner oder gleich und mindestens n-np Werte größer oder gleich
Qp.
Es ergeben sich besondere Quantile:
Der Median = Q0,5 teilt die Reihe in zwei Hälften.
Mindestens die Hälfte der gemessenen Werte soll größer oder gleich,
mindestens die Hälfte der gemessenen Werte soll kleiner oder gleich dem Median sein.
Beispiel: 2 2 3 3 4 4 4 5 5 5 7 8 8 8 8 8 8 8 8 8 10 12
np=11 ist natürlich
Median = 0,5(11. Wert + 12. Wert) = 0,5(7+8) = 7,5
(11 Werte sind kleiner gleich, 11 Werte größer gleich 7,5).
Das 1. Quartil = Q0,25 teilt die ersten 25 % der Messwerte ab.
Beispiel: 2 2 3 3 4 4 4 5 5 5 7 8 8 8 8 8 8 8 8 8 10 12
np = 5,25 nicht natürlich
1. Quartil = 6. Wert = 4
Mindestens ein Viertel der Werte sind kleiner gleich 4 und mindestens drei Viertel
der Werte größer oder gleich 4.
Das letztes Quartil = Q0,75 teilt die letzten 25 % der Messwerte ab.
Beispiel: 2 2 3 3 4 4 4 5 5 5 7 8 8 8 8 8 8 8 8 8 10 12
np = 15,75 nicht natürlich
letztes Quartil = 16. Wert = 8
Mindestens drei Viertel der Werte sind kleiner gleich 8 und mindestens ein Viertel
der Werte größer oder gleich 8.
Das 1. Perzentil = Q0,1 teilt die ersten 10 % der Messwerte ab.
Beispiel: 2 2 3 3 4 4 4 5 5 5 7 8 8 8 8 8 8 8 8 8 10 12
np = 2,2 nicht natürlich
1. Perzentil = 3. Wert = 3
Mindestens 10 % der Werte sind kleiner gleich 3 und mindestens 90 %
der Werte größer oder gleich 3.
Zu den Quantilen kann man ein sogenanntes Boxplot-Diagramm zeichnen. Man
kennzeichnet Messgrenzen, 1. Quartil, Median, letztes Quartil. In der Box liegen mindestens
die Hälfte der Messwerte und mindestens die Hälfte der Messwerte liegt bis zum Median.
Beispiel:
0
2
4
7,5
8
12
15
Hinweis: Gibt man den Median als Mittelwert an, so finden wenige ausreißende Werte keine
Beachtung, beim arithmetischen Mittel = Durchschnittswert schon.
Streumaße
Streumaße geben die Schwankung der Meßwerte an.
Spanne:
Maximaler Wert minus minimaler Wert
Beispiel: 12 – 2 = 10
Varianz:
Summe der quadrierten Abweichungen der Messwerte vom arithmetischen Mittel,
n
multipliziert mit den entsprechenden relativen Häufigkeiten: :
V=
 (x
i 1
i
 x) 2 ri
Beispiel:
V  (2  6, 27)2 
2
2
3
3
1
9
1
1
 (3  6, 27)2   (4  6, 27)2   (5  6, 27)2   (7  6, 27) 2   (8  6, 27)2   (10  6, 27)2   (12  6, 27)2 
22
22
22
22
22
22
22
22
= 6,97
Standardabweichung:
Wurzel aus der Varianz:   V
Beispiel:   6,97  2,6