3. Deskriptive Statistik Ziel der deskriptiven (beschreibenden

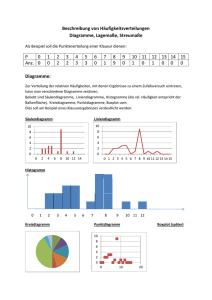
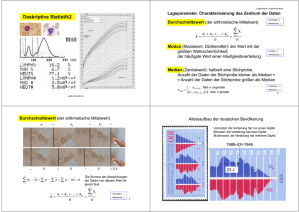
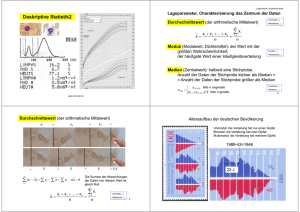
3. Deskriptive Statistik
Ziel der deskriptiven (beschreibenden) Statistik (explorativen
Datenanalyse) ist die übersichtliche Darstellung der wesentlichen in den erhobenen Daten enthaltene Informationen (Strukturen).
3.1. Univariate Verteilungen
Eindimensionale (univariate) Daten:
Pro Objekt wird ein Merkmal durch
Messung / Befragung/ Beobachtung
erhoben.
Resultat ist jeweils ein Wert
(Mermalsausprägung) xi:
- Länge eines Werkstücks,
- Gehalt einer Person,
- Güteklasse eines Produkts
Zweidimensionale (bivariate) Daten:
Pro Objekt werden zwei Merkmale
erhoben:
(Preis, Material)
(Ausbildung, Gehalt)
(Wohngegend, Wagentyp)
Ausgangspunkt: sog. Urliste
= Ergebnis der Registrierung der Beobachtungen
(Mermalsausprägungen)
x1 , x 2 , . . . , x n
(häufig Zahlenkodes)
1
Beispiel 1: benutzte Verkehrsmittel von 100 Urlaubern bei
Auslandsreisen,
53 x Pkw, 29 x Flugzeug, 7 x Bahn, 9 x Bus, 2 x Sonstige
Beispiel 2: Messwerte für einen technischen Parameter an 10
Werkstücken (geordnet)
1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,17 1,17 1,18
Beispiel 3: 200 Messwerte in Klassen
Klasse
Häufigkeit
125,5 ... 130,5 8
130,5 ... 135,5 28
135,5 ... 140,5 36
140,5 ... 145,5 36
145,5 ... 150,5 50
150,5 ... 155,5 40
155,5 ... 160,5 2
Erster Schritt:
Bestimmung der absoluten Häufigkeiten für das Auftreten der
verschiedenen Merkmalsausprägungen (bzw. Klassen)
d.h. Erstellen einer Häufigkeitstabelle, Häufigkeitsverteilung
(Verteilung)
2
Grafische Darstellung der Verteilung der
Merkmalsausprägungen einer Variablen
• Balkendiagramm, ( -grafik, Säulendiagramm)
Veranschaulichung absoluter Häufigkeiten,
z.B:
Darstellung der Ausprägungen auf der x-Achse,
Häufigkeiten auf der y-Achse
zur
• pro Ausprägung ein Balken, eine Säule,
• im Beispiel Darstellung von Kategorien:
– Balken getrennt
– günstig bei kategorialen Daten mit wenigen Kategorien
– Reihenfolge der Anordnung (auf der x-Achse) spielt
keine Rolle
• Korrekte Skalierung der Achsen !
relative Häufigkeiten =
absolute Häufigkeiten
Gesamtanzahl der Beobachtungen
• nützlich beim Vergleich von Anteilen, günstig durch
mehrere Kreisdiagramme oder gestapelte Balkendiagramme darstellbar
• absolute Häufigkeiten nicht mehr zu erkennen, keine
Aussagen z.B. über Zunahme der abs. Häufigkeiten möglich
3
• bei metrischen Daten u.U. Anzahl der Säulen bzw.
Sektoren zu groß, da zu viele verschiedene Messwerte
vorliegen
• Ausweg: Klasseneinteilung, Bildung von sog. Messwertklassen, Daten werden gruppiert, siehe Beispiel 3, dann
grafische Darstellung durch Histogramm
• oftmals werden die Werte für die Klassenmitten
verbunden (mind. ordinale Daten):
Häufigkeitspolygon, liefert Information über die Form
der Verteilung
• kumulative Häufigkeiten entstehen durch Aufsummieren
der abs. Häufigkeiten, von links beginnend
mindestens ordinale Daten erforderlich, Beispiel 3:
Klasse
Häufigkeit kumulative Häufigkeiten
125,5 ... 130,5 8
8
130,5 ... 135,5 28
8+28=36
135,5 ... 140,5 36
36+36=72
140,5 ... 145,5 36
72+36=108
145,5 ... 150,5 50
108+50=158
150,5 ... 155,5 40
158+40=198
155,5 ... 160,5 2
198+2=200
” 158 Messwerte waren ≤ 150, 5 cm ”
Bild der kumulativen Häufigkeiten ist das
Summenpolygon bzw. die empirische Verteilungsfunktion für die kumulierten relativen Häufigkeiten
4
Kenngrößen eindimensionaler Verteilungen
• Charakterisierung von Verteilungen durch statistische
Maßzahlen
(Kenngrößen,
Parameter),
die
die
Eigenschaften (Zentrum, Ausbreitung, Form) der
Verteilung widerspiegeln
• wichtigste Maßzahlen sind Lage- und Streuungsparameter
• Wichtig: Skalierungsniveau beachten
Lageparameter:
Der Modalwert
• = die am häufigsten auftretende Merkmalsausprägung
• = die Klasse (Klassenmitte) mit der größten Häufigkeit
bei gruppierten Daten (Klassen)
• Mehrere Maxima: kein Modalwert
• Eigenschaften und Interpretation:
– Wert, der ”am ehesten” zu beobachten ist
(sprachl. Formulierungen wie:
”Diese Krankheit dauert normalerweise 3 Tage.”,
”Die Fahrzeit beträgt normalerweise 2 Stunden.”)
– unempfindlich
Werten)
gegenüber
5
Ausreißern
(extremen
Median
• mindestens ordinale Daten
• Median heißt jede Merkmalsausprägung a, für die gilt:
X
i : xi ≤a
hi ≥ 1/2 ,
X
i : xi ≥a
hi ≥ 1/2
• ”oberhalb” und ”unterhalb” der Mediane befinden sich
gleichviele Elemente der Stichprobe
• Bei metrischen Daten wird häufig der Mittelwert der
Mediane als Median angegeben.
• Eigenschaften und Interpretation:
– zentraler Wert bei ordinalen Merkmalen
– unempfindlich gegenüber Ausreißern
– Minimaleigenschaft bez. absoluter Abweichungen
(metrische Daten), jeder Median löst
n
X
i=1
|xi − z| → min
Das arithmetische Mittel
• metrische Daten
x̄ =
1
n
n
X
i=1
xi =
l
X
j=1
aj hj
• Eigenschaften und Interpretation:
– Schwerpunkt der Verteilung,
– empfindlich gegenüber Ausreißern (vgl. Median),
6
– Minimaleigenschaft bezüglich quadratischer
Abweichungen:
n
X
i=1
(xi − z)2 → min
hat die Lösung z = x̄ (Beweis: Übung).
• bei gruppierten Daten mit Klassenmitten x∗i und
Klassenhäufigkeiten ni:
1
x̄ =
n
k
X
i=1
nix∗i
gewichtetes Mittel der Klassenmitten
Beispiel 3: 200 Messwerte in Klassen
Klasse
Häufigkeit
125,5 ... 130,5 8
130,5 ... 135,5 28
135,5 ... 140,5 36
140,5 ... 145,5 36
145,5 ... 150,5 50
150,5 ... 155,5 40
155,5 ... 160,5 2
• Im Gegensatz zum Median kann das arithmetische Mittel
bei
gruppierten
Daten
mit
offenen
Randklassen nicht berechnet werden.
7
Streuungsparameter (Variabilitätsparameter)
• Maßzahlen zur Bewertung der Variabilität der Messwerte, der Breite einer Verteilung, der Abweichungen vom
Mittelwert
• Ziel von Analysen: Zerlegung der Variabilität der
Messwerte nach verschiedenen Ursachen (Faktoren, Fehler
des Messgerätes usw.), Analyse der Wirkung des Zufalls
Streuungsparameter für metrische Daten
• Spannweite: v = xmax − xmin
• empirische Varianz: s2
1
s =
n−1
2
n
X
i=1
¶
n
1 µX
2
2
(xi − x̄) =
x − nx̄
n − 1 i=1 i
2
”mittlere quadratische Abweichung”
1
2
(· − ·)
n−1
Dimension von s2 :
ist z.B. xi eine Konzentration, dann mg 2/l2
• Eigentlich müsste durch n geteilt werden. Grund für die
Division durch n − 1 ist die Anwendung der so
erhaltenen Größe in der schließenden Statistik.
√
• Standardabweichung s = s2, gleiche Dimension wie xi.
s
dimensionslos
• Variationskoeffizient v = 100%
x̄
8
Quartilsabstand
• Grundgedanke:
Ähnlich der Spannweite (s.o.) wird die ”Spannweite der
mittleren 50% der Werte” berechnet.
• Unteres Quartil q0.25 heißt jede Merkmalsausprägung a,
für die gilt:
X
i : xi ≤a
hi ≥ 1/4 ,
X
i : xi ≥a
hi ≥ 3/4 .
Oberes Quartil q0.75 heißt jede Merkmalsausprägung a, für
die gilt:
X
i : xi ≤a
hi ≥ 3/4 ,
X
i : xi ≥a
hi ≥ 1/4 .
• q0.25 und q0.75 sind i.A. nicht eindeutig bestimmt. Falls
doch, dann heißt
q0.75 − q0.25
(empirischer) Quartilsabstand,
Interquartilbereich, IQR.
• In Statistiksoftware sind unterschiedliche Interpolationsregeln für die Quartile realisiert.
9
• Veranschaulichung von Median,
Minimum, Maximum im Boxplot:
Quartilen,
IQR,
← Ausreißer (mit Fallnummer)
← maximale Zaunlänge
= 1,5 · Boxlänge
← oberes Quartil
←
Median
← unteres Quartil
← kleinster Wert, der nicht als
Ausreißer erkannt wird
Beispiel: ALLBUS, Monatliches Haushalt-Nettoeinkommen (die
ersten 300 Fälle, nur 178 haben geantwortet).
10