Werbung

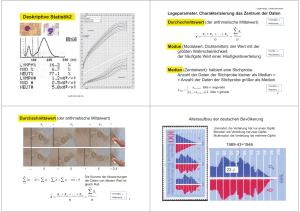
Lagemasse, Lokationsmasse Lageparameter. Charakterisierung das Zentrum der Daten Deskriptive Statistik2 Durchschnittswert (der arithmetische Mittelwert) =average(...) =Mittelwert(...) n x + x2 + K + xn x= 1 = n ∑x i =1 i n Modus (Modalwert, Dichtemittel): der Wert mit der größten Wahrscheinlichkeit; der häufigste Wert einer Häufigkeitsverteilung =mode(...) =Modalwert(...) Median (Zentralwert): halbiert eine Stichprobe. Anzahl der Daten der Stichprobe kleiner als Median = = Anzahl der Daten der Stichprobe größer als Median ⎧ x( n +1) / 2 falls n ungerade xmed = ⎨ ⎩( x n / 2 + x( n / 2+1) ) / 2 falls n gerade =median(...) =Median(...) 2 KAD 2015.09.16 Durchschnittswert (der arithmetische Mittelwert) + x1 + x2 x3 Altersaufbau der deutschen Bevölkerung = Unimodal: die Verteilung hat nur einen Gipfel Bimodal: die Verteilung hat zwei Gipfel. Multimodal: die Verteilung hat mehrere Gipfel. 1989-43=1946 = n ∑ (x i =1 i + x x − x ) = ∑ xi − ∑ x = ∑ xi − n x = 0 + x =3x 23 J Die Summe der Abweichungen der Daten von diesem Wert ist gleich Null. n x= x1 + x 2 + K + x n = n ∑x i =1 n i =average(...) =Mittelwert(...) 3 4 Weitere Beispiele Linkssteile bzw. rechtsschiefe Verteilung f(x) =skew(...) > 0 =Schiefe(...) > 0 MaxwellBoltzmannVerteilung x Modus Median Durchschnitt Komplexität der Tiere z.B. Einkommensverteilungen in einem Land: Der Großteil der Bevölkerung verdient relativ wenig, während es nur wenig Leute gibt, die sehr viel verdienen. 5 6 www.vordenker.de/if_gould/images/verteilung.gif Linksschiefe bzw. rechtssteile Verteilung Daten und ihre Durchschnittswerte f(x) =skew(...) < 0 =Schiefe(...) < 0 Durchschnitt Median Modus Die Daten streuen um den Durchschnittswert. x z.B. Dauer einer Schwangerschaft 7 Pulsfrequenzen (1/Min) Pr.Buch Abb. 10 8 Streuungsmasse (Variabilitätsmaße, Variationsmaße) Mass für die Streubreite von Daten Streuungsparameter. Charakterisierung der Variation der Daten Standardabweichung (Streuung der Messdaten, s): die mittlere Abweichung vom Durchschnitt: das Quadrat der Streuung, die mittlere quadratische Abweichung, auch als Varianz bezeichnet: Spannweite: xmax-xmin n s= ∑(x i =1 i − x) 0 <α <1 (seien dazu die xi aufsteigend sortiert): falls nα keine ganze Zahl ist ⎧ x xα = ⎨ [nα ]+1 ⎩( x nα + x nα +1 ) / 2 falls nα ganzzahlig ist 2 n −1 α-Quantil =stdev(...) =Stabw(...) x1/4 – unteres Quartil x3/4 – oberes Quartil x1/10 – unteres Dezil x9/10 – oberes Dezil =Quartil(...) halber Quartilabstand : (x3/4 – x1/4)/2 n s2 = ∑ ( x i − x )2 i =1 n −1 =var(...) =Varianz(...) =max(...)-min(...) mit Wörter: z.B. Dezile Durch Dezile (lat. „Zehntelwerte“) wird die Verteilung in 10 gleich große Teile zerlegt. Unterhalb des dritten Dezils liegen 30 % der Verteilung. 9 10 f(x) rechtsschiefe Verteilung Perzentilenkurven sind ein Werkzeug für den Arzt. x Modus Median Durchschnitt Wachstums- und Gewichtskurven für Mädchen =percentile(...) =Quantil(...) 11 Skalentypen zulässige LageParameter zulässige StreuungsParameter Nominalskala Modus – Ordinalskala Modus, Median – numerische Skalen Modus, Median, Durchschnittswert Spannweite, Quartilabstand, Standardabweichung 12 Häufigkeitsverteilung Häufigkeitsdichte h: Körperhöhe ΔN Δh ΔN Δh H: kollektive Höhe, Gesamthöhe Spektrum ΔH Δh ⎛ 1 ⎞ ⎜⎜ ⎟⎟ ⎝ 10 cm ⎠ ⎛ 1 ⎞ ⎜⎜ 10 cm ⎟⎟ ⎝ ⎠ Fläche unter der Kurve: n ΔH Δh Fläche unter der Kurve: H H h 160 170 180 190 200 210 Spektrum als eine spezielle Häufigkeitsverteilung 13 160 170 180 190 200 210 h (cm) h (cm) 14 Position des Medians und des Durchschnitts einer Verteilung (1) Emissionsspektrum: wie verteilt sich die emittierte Energie über die Photonenenergien ΔE Δε ΔN Δx Apunktierte = Aschraffierte 50% 50% charakteristische Größe des Energietransports: Intensität ΔJ Δλ x ΔN Δx J Median Schwerlinie Benützung der Wellenlänge ist bequemer als die der Photonenenergie 15 Durchschnitt x 16 Ergänzungsmaterial Summen- (kumulierte/kumulative) Häufigkeitsverteilung Position des Medians und des Durchschnitts einer Verteilung (2) Flächenhalbierungslinie der Häufigkeitsverteilung ΔH Δh ΔN Δh N SummenHäufigkeitsverteilung Flächenhalbierungslinie des Spektrums 14 10 8 6 4 2 0 150 ΔN Δh ⎛ 1 ⎞ ⎜⎜ ⎟⎟ ⎝ 10 cm ⎠ HäufigkeitsdichteVerteilung M=N0-N 0 Median „SummenHäufigkeitsverteilung” h Durchschnittswert relative „SummenHäufigkeitsverteilung” kumulatives Überleben nach der Operation 170 180 190 200 210 220 h (cm) 5 DD-”Spektrum” 4 3 2 1 160 170 180 190 200 210 220 14 12 ID-”Spektrum” 10 8 6 4 2 0 150 17 160 6 0 150 0 Wieviele Werte sind kleiner als h? 12 h (cm) Wieviele Werte sind grösser als h? h (cm) 160 170 180 190 200 210 220 18 Überlebenskurven Quantile und die relative Summenhäufigkeitsverteilung Wirkung der Chemotherapie. Pankreaskarzinom rot: ohne Gemcitabin Fi grün: mit Gemcitabin (Chemotherapie) 0,9 0,75 Coulter Zähler 1 0,25 0,1 x xmax xmin unteres oberes unteres Quartil Quartil Dezil oberes Dezil Quartilabstand Überleben, Tage 20