Quartile und Boxplots 8.4

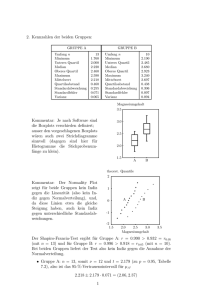
Statistik | Quartile und Boxplots
8.4 Quartile und Boxplots
Quartile und Boxplots
Der Boxplot ist ein Diagramm, das schnell einen Eindruck vermittelt, in welchem
Bereich die Daten liegen und wie sie sich über diesen Bereich verteilen. Gewisse
Kennwerte können direkt aus der grafischen Darstellung abgelesen werden.
Ein Boxplot besteht immer aus einem Rechteck, genannt Box, und zwei Linien,
die dieses Rechteck verlängern. Diese Linien werden als Whisker oder
Antennen bezeichnet und durch einen Strich abgeschlossen. Das Ende der
Antennen entspricht in der Regel dem Minimum bzw. Maximum der Liste.
unteres
Quartil
qu Median
unterer
Whisker
oberes
Quartil
qo
oberer
Whisker
Skala
!
Quartile [lat.]
Viertelwerte
U
U
Die Box entspricht jenem Bereich, in dem die mittleren 50 % der Daten liegen. Sie wird vom Median qu (unteres Quartil) der unteren Hälfte der Daten
und vom Median qo (oberes Quartil) der oberen Hälfte der Daten begrenzt.
1. Viertel
Min
2. Viertel
unteres
Quartil qu
3. Viertel
4. Viertel
oberes
Quartil qo
Median
untere Hälfte
Max
obere Hälfte
Quartilsabstand q
U
Der Datensatz wird beim Boxplot in vier gleiche Teile (Quartile) geteilt.
U
Den Unterschied zwischen unterem und oberem Quartil nennt man
Quartilsabstand q.
Beispiel:
2, 3, 4, 5, 6, 6, 6,
Ermittle für die Datenliste den Median, unteres und
7, 7, 8, 9, 10, 12,
oberes Quartil, Minimum (min) und Maximum (max).
12, 16, 16, 17
Zeichne den Boxplot und notiere zusätzliche Informationen, die du unmittelbar aus dem Boxplot entnehmen kannst.
Lösung
Median = 7;
qu = 6; qo = 12;
Min = 2; Max = 17 0
qu
Min
2
4
6
z
qo
8
10
12
Max
14
Mindestens 25 % der Daten sind kleiner oder gleich qu = 6.
Mindestens 25 % der Daten sind größer oder gleich qo = 12.
Mindestens 50 % aller Daten liegen zwischen qu = 6 und qo = 12.
aus: EXPEDITION MATHEMATIK 4, Kraker, Plattner, Preis, E. Dorner-Verlag, 2010
16