Inhaltsverzeichnis - Freiburger Verlag

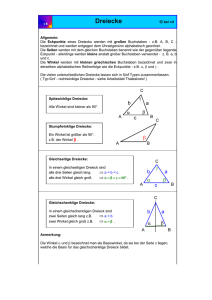
Inhaltsverzeichnis
Inhaltsverzeichnis
Einleitung
5
1
Zahlen
7
1.1
Zahlen und Zahlenmengen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.2
Rechnen mit Zahlen und Termen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.3
Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.4
Gleichungssysteme mit zwei Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.5
Textaufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.6
Prozentrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2
3
4
5
Leitidee Messen
14
2.1
Länge, Fläche und Volumen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.2
Gewicht und Masse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
2.3
Zeiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
2.4
Winkel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
Leitidee Raum und Form
20
3.1
Dreiecke
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3.2
Vierecke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
3.3
Körper . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
3.4
Achsensymmetrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
3.5
Spiegelungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
Leitidee Funktionaler Zusammenhang
28
4.1
Proportionale Zuordnungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
4.2
Proportionale Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
4.3
Antiproportionalität
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
4.4
Lineare Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
4.5
Anwendungen von linearen Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
Leitidee Daten und Zufall
34
5.1
Häufigkeiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
5.2
Diagramme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
5.3
Mittelwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
5.4
Wahrscheinlichkeiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
Tipps
41
Lösungen
50
Freiburger-Verlag.de
3
Inhaltsverzeichnis
4
Freiburger-Verlag.de
3. Leitidee Raum und Form
3
Leitidee Raum und Form
Tipps ab Seite 13, Lösungen ab Seite 15
Bei dieser Leitidee geht es darum, dass Du die wichtigsten geometrischen Formen wie Dreiecke und Vierecke kennst
und mit ihnen umgehen kannst. Dazu gehören vor allem Flächenberechnungen, aber auch Symmetrien, Winkel und
Konstruktionen.
3.1 Dreiecke
Für alle Dreiecke gilt:
• Seiten und Winkel liegen sich gegenüber, also a und α , b und β sowie
c und γ .
• Die Winkelsumme ist 180 ◦, d.h. α + β + γ = 180 ◦.
• Der Umfang u ist die Summe der Seiten: u = a + b + c
• Eine Höhe h steht immer senkrecht auf der dazugehörigen Seite.
• Die Fläche A wird berechnet mit der Formel «Grundseite mal Höhe
durch zwei», dabei kann jede Seite die Grundseite sein:
A=
a·ha
2
=
b·hb
2
=
c·hc
2
Für rechtwinklige Dreiecke gilt:
• Es gilt der Satz des Pythagoras: a2 + b2 = c2 , wobei c die Seite gegenüber des rechten Winkels ist.
• Wenn γ der rechte Winkel ist, gilt: α = 90 − β und entsprechend
β = 90 − α .
• Die Fläche A kann man besonders einfach berechnen, wenn man a
und b kennt: A = a·b
2 , da dann a = hb bzw. b = ha
Für gleichschenklige Dreiecke gilt:
• Zwei Winkel sind gleich groß
• Zwei Seiten sind gleich lang
• Die Höhe hc kann man mit dem Satz des Pythagoras berechnen:
2
h2c = a2 − 2c
Für gleichseitige Dreiecke gilt:
• Alle Winkel betragen 60 ◦
• Alle Seiten sind gleich lang
• Alle Höhen kann man mit dem Satz des Pythagoras berechnen:
√
2
h2 = a2 − 2a = 43 a2 ⇒ h = a2 · 3
Aufgaben
a) Konstruiere ein Dreieck mit den angegebenen Maßen und beschreibe die Konstruktion mit eigenen Worten.
I) a = 3 cm, b = 4 cm, c = 5 cm
Freiburger-Verlag.de
II) a = 3, 5 cm, c = 4 cm, α = 40 ◦ , γ < 90◦
5
3. Leitidee Raum und Form
b) Nachfolgend sind die Werte von verschiedenen Dreiecken angegeben. Begründe, welche Dreieckskonstruktion nicht möglich ist.
I)
a = 3, 5 cm b = 4 cm
II)
b = 2, 5 cm c = 2, 5 cm β = 123◦
III) α = 55◦
c)
β = 75◦
c = 5 cm
γ = 60◦
Anna will die Fläche des abgebildeten Dreiecks berechnen und überlegt,
wie sie die Höhe hc herausbekommen kann. Christian sagt dazu nur:
«nimm doch einfach die Seiten a und b, damit geht es einfacher». Hat
er recht? Erläutere seinen Lösungsweg.
3.2 Vierecke
Im Gegensatz zu den Dreiecken gibt es sehr viel mehr verschiedene Vierecke. Gemeinsam haben alle Vierecke, dass
die Winkelsumme ihrer Innenwinkel 360◦ beträgt.
Das Quadrat
• Ein Quadrat besitzt vier rechte Winkel
• Alle Seiten sind gleich lang
• Die Länge der Diagonale beträgt d =
√
√
a2 + a 2 = a 2
• Der Flächeninhalt beträgt: A = a2
Der Umfang beträgt: u = 4a
Das Rechteck
• Ein Rechteck besitzt vier rechte Winkel
• Gegenüberliegende Seiten sind gleich lang.
• Der Flächeninhalt beträgt: A = a · b
Der Umfang beträgt: u = 2a + 2b
• Die Diagonalen sind gleich lang und halbieren sich.
Das Parallelogramm
• Gegenüberliegende Seiten sind gleich lang.
• Gegenüberliegende Winkel sind gleich groß.
• Die Fläche beträgt: A = a · ha = b · hb
Der Umfang beträgt: u = 2 · a + 2 · b
• Die Diagonalen sind verschieden lang
Die Raute
• Eine Raute ist ein Parallelogramm mit gleich langen Seiten.
• Alle Seiten sind gleich lang.
• Gegenüberliegende Winkel sind gleich groß.
• Die Diagonalen c und d stehen senkrecht aufeinander und teilen
die Raute in vier deckungsgleiche rechtwinklige Dreiecke.
• Der Flächeninhalt beträgt: A = 12 · c · d
Der Umfang beträgt: u = 4 · a
6
Freiburger-Verlag.de
3. Leitidee Raum und Form
Der Drachen
• Je zwei benachbarte Seiten sind gleich lang.
• Die Diagonalen c und d stehen senkrecht aufeinander.
• Der Flächeninhalt beträgt: A = 21 · c · d
Der Umfang beträgt: u = 2 · a + 2 · b
Das Trapez
• Zwei gegenüberliegende Seiten sind parallel.
• Die Linie m teilt die beiden nicht-parallelen Strecken in der Mitte,
ihre Länge beträgt a+c
2
• Der Flächeninhalt beträgt: A = m · h =
Der Umfang beträgt: u = a + b + c + d
a+c
2
·h
Aufgaben
a) Konstruiere ein Parellelogramm mit folgenden Maßen: a = 3, 5 cm, b = 2 cm, h a = 1, 5 cm
b) Konstruiere eine Raute mit a = 2 cm und α = 50◦
c) Konstruiere einen Drachen mit a = 1, 5 cm, b = 2, 5 cm und d = 4, 5 cm.
d) Konstruiere ein Trapez mit a = 5 cm, b = 2 cm, d = 2, 5 cm und h = 1, 5 cm.
e) Christoph beschreibt die Eigenschaften geometrischer Figuren. Birgit hält dagegen: «Bei manchen Sachen
hast du nicht genau nachgedacht...» Wo hat Christoph recht? Begründe deine Antworten und gib in der rechten
Spalte ein Beispiel oder ein Gegenbeispiel an.
Ein Viereck ist immer ein Rechteck, wenn
gegenüberliegende Seiten gleich lang sind.
richtig falsch
Wenn ich die Fläche eines Parallelogramms
berechnen will, kann ich dazu die Höhe auf a
oder b konstruieren und erhalte entsprechend
A = a · ha bzw. A = b · hb
richtig falsch
Bei einer Raute sind alle Winkel gleich groß.
richtig falsch
Bei einem Drachen sind die gegenüberliegenden Winkel gleich groß.
richtig falsch
f) Berechne den Inhalt der grau gezeichneten Fläche, schreibe deinen Rechenweg auf. Alle Maße sind in cm
angegeben.
Freiburger-Verlag.de
7
3. Leitidee Raum und Form
Rechenweg:
g) Eva will die grau gezeichnete Fläche berechnen. Sie geht folgendermaßen vor:
A = (b − c) · d + (b − c) · (a − d) + c · (a − d)
I) Zeichne das Element (b − c) · (a − d) in die Figur ein.
II) Geht es auch einfacher? Beschreibe einen direkteren Weg.
3.3 Körper
Der Würfel
• Alle Innenwinkel des Würfels sind rechte Winkel
• Alle Kanten eines Würfels sind gleich lang.
• Das Volumen beträgt: V = a · a · a = a3
Die Oberfläche beträgt: O = 6 · a2
√
• Die Länge der Raumdiagonalen d beträgt: d = a 3
Der Quader
• Alle Innenwinkel eines Quaders sind rechte Winkel.
• Alle parallelen Kanten sind gleich lang
• Das Volumen beträgt: V = a · b · c
Die Oberfläche beträgt: O = 2 · a · b + 2 · a · c + 2 · b · c
Aufgaben
a) Berechne das Volumen und die Oberfläche folgender Körper:
I) Würfel mit Kantenlänge 2, 5 cm.
II) Quader mit den Kantenlängen a = 2 m, b = 3 m, c = 5 m
b) Bei einem Quader beträgt die Länge 1 m. Die Breite soll das Doppelte, die Höhe das Dreifache der Länge
betragen. Berechne das Volumen.
3.4 Achsensymmetrie
Eine Figur ist achsensymmetrisch, wenn sie mindestens eine Symmetrieachse besitzt:
8
Freiburger-Verlag.de
3. Leitidee Raum und Form
Eine Figur kann dabei eine oder mehrere Symmetrieachsen besitzen:
Aufgaben
a) Zeichne alle Symmetriachsen ein
b) Wie viele Symmetrieachsen besitzt
I) Ein Rechteck
II) Ein Parallelogramm
III) Ein Fünfeck
IV) Ein Kreis
c) Welche Abbildung zeigt alle Symmetrieachsen?
Freiburger-Verlag.de
9
3. Leitidee Raum und Form
3.5 Spiegelungen
Bei einer Spiegelung einer Figur an einer Achse entsteht ein Spiegelbild.
• Der Abstand von einem Punkt zur Spiegelachse ist genauso groß wie der Abstand vom Spiegelpunkt zur
Achse.
• Die Spiegelpunkte werden mit dem gleichen Buchstaben und einem kleinen Strich gekennzeichnet: P 0 ist der
Spiegelpunkt von P.
• Eine Gerade, die senkrecht zur Spiegelachse steht, hat sich selbst als Spiegelgerade.
• Der Umlaufsinn der Eckpunkte einer Figur dreht sich bei der Spiegelung um. (ABC wird in der Figur im
Gegenuhrzeigersinn durchlaufen, A0 B0 C0 wird im Uhrzeigersinn durchlaufen)
Beispiele:
• Gesucht ist die Spiegelfigur der angegebenen Figur an der gezeichneten Spiegelachse.
Um die Figur an der Achse zu spiegeln, musst Du jeden Eckpunkt der Figur an der Achse spiegeln. Dazu
zeichnetst Du mit Hilfe des Geodreiecks Hilfslinien, die senkrecht zu der Spiegelachse sind und durch die Eckpunkte gehen (linke Zeichnung). Anschließend misst Du die Abstände von der Spiegelachse zu den Punkten
und trägst sie in die andere Richtung auf den Hilfslinien ab. Du erhälst die Spiegelpunkte A 0 , B0 , C0 , und D0
(rechte Zeichnung):
Du kannst hier auch wieder sehen, dass sich der Umlaufsinn umgekehrt hat: In der Figur ABCD durchläuft
man die Eckpunkte im Gegenuhrzeigersinn, in der gespiegelten Figur durchläuft man die Punkte im Uhrzeigersinn.
10
Freiburger-Verlag.de
3. Leitidee Raum und Form
• Gesucht ist die Spiegelachse, an der die Figur gespiegelt wurde:
Lösung:
– Zuerst verbindest Du «gleiche» Ecken miteinander (linke Zeichnung)
– Nun bestimmst Du die Mittelpunkte der Hilfslinien (mittlere Zeichnung)
– Durch diese Punkte wird eine Linie gezogen, dies ist die Spiegelachse, die die Hilfslinien senkrecht
schneidet.
Aufgaben
a) Spiegele die Figuren an der Achse:
b) Bestimme jeweils die Spiegelachse
Freiburger-Verlag.de
11
3. Leitidee Raum und Form
c) Zeichne ein Dreieck mit den drei Eckpunkten ABC; zeichne den Umlaufsinn ein. Zeichne nun eine Gerade
und spiegele das Dreieck an dieser Geraden. Zeichne eine weitere Gerade und spiegele das Spiegeldreieck an
dieser Geraden. Welche Richtung hat der Umlaufsinn nun?
d) Spiegele die Geraden a, b und c an der Spiegelachse s. Welche Figur entsteht?
e) Gegeben sind die Punkte A, B und der Spiegelpunkt A 0 von A. Konstruiere den Spiegelpunkt B 0 von B.
12
Freiburger-Verlag.de
Tipps
3
3. Leitidee Raum und Form
Leitidee Raum und Form
3.1 Dreiecke
a)
I) Zeichne zuerste die Seite c des Dreiecks ein. Trage dann die Länge der beiden anderen Seiten mit dem
Zirkel ab. Wo sich die beiden Kreise schneiden, befindet sich der Punkt C.
II) Beginne auch hier mit der Seite c. Zeichne nun die Seite b mit Hilfe des Winkels α ein. Zur Bestimmung
von Punkt C trägst Du die Länge von Seite a mit dem Zirkel vom Punkt B aus ab. Wo die Kreislinie die
Seite b schneidet, liegt der Punkt C.
b) Versuche, die Dreiecke zu skizzieren. Beachte die sich ergebende Winkelsumme.
c) Überlege, wie man den Flächeninhalt eines rechtwinkligen Dreiecks berechnen kann.
3.2 Vierecke
a) Zeichne zuerst die Seite a des Parallelogramms. Anschließend konstruierst Du eine zu a parallele Linie im
Abstand von 1, 5 cm. Anschließend trägst Du die Länge der Seite b mit dem Zirkel auf dieser zwei Mal ab.
b) Beginne mit einer Seite der Raute und zeichne die zweite Seite unter einem Winkel von 50 ◦ ein. Da bei einer
Raute alle Seiten gleich lang sind, kannst Du nun die anderen Seiten einzeichnen, indem Du parallele Linien
konstruierst.
c) Beginne mit der Diagonalen d. Trage anschließend die Länge der beiden anderen Seiten an den Enden dieser
Diagonalen mit dem Zirkel ab. An den Schnittpunkten der Kreislinien, befinden sich die weiteren Punkte des
Drachen.
d) Beginne mit der Grundlinie a des Trapezes. Anschließend konstruierst Du die Höhe und eine zu a parallele
Linie. An den Enden der Linie a trägst Du mit dem Zirkel die Längen der Seiten b und d ab um die fehlenden
zwei Eckpunkte zu bestimmen.
e) Nimm eventuell die Einführungen auf den Seiten 5 und 6 zu Hilfe um die Behauptungen zu untersuchen.
f) Es gibt verschiedene Wege, die graue Fläche zu berechnen: Entweder berechnest Du zuerst die Fläche eines
großen Rechtecks, von dem Du die Fläche eines kleinen Rechtecks abziehst oder Du teilst die Fläche in
mehrere Einzelflächen auf, die Du berechnest und anschließend addierst.
g) Lies an der Zeichnung ab, welche Seiten die Längen (b − c) und (a − d) haben. Die Fläche kannst Du auch
berechnen, indem Du zuerst die Fläche des großen Rechtecks berechnest und dann die Fläche des Rechtecks
«links oben» abziehst.
3.3 Körper
a)
I) Benutze die Formeln zur Volumenberechnung V = a3 und zur Oberflächenberechnung O = 6 · a2.
II) Benutze die Formeln: V = a · b · c und O = 2 · a · b + 2 · a · c + 2 · b · c.
3.4 Achsensymmetrie
a) Um herauszufinden, ob eine Achse eine Symmetrieachse ist, hilft es, wenn Du dir vorstellst, dass auf dieser
Achse ein Spiegel stehen würde. Das Spiegelbild muss dann genauso aussehen wie die zweite Hälfte des
Bildes in der Zeichnung.
b) Mit jedem Bild kommen neue Achsen hinzu. Eine Achse ist dann keine Symmetrieachse mehr, wenn die Figur
nicht symmetrisch zu dieser Achse liegt.
c) Überlege, welche der Achsen keine Spiegelachsen sind.
Freiburger-Verlag.de
13
3. Leitidee Raum und Form
Tipps
3.5 Spiegelungen
a) Um die Figuren an der Achse zu spiegeln, spiegelst Du am besten die Ecken an der Achse. Zeichne dazu
Hilfslinien, die senkrecht auf der Achse stehen. Trage dann den Abstand des Punktes mit dem Geodreieck
oder dem Zirkel ab, um die Spiegelpunkte zu konstruieren.
b) Verbinde jeden Punkt mit seinem Spiegelpunkt und halbiere die entstandenen Strecken. Die Spiegelachse
verläuft durch die Mittelpunkte dieser Strecken.
c) Überlege, was bei jeder Spiegelung mit dem Umlaufsinn geschieht.
d) Um die Geraden zu spiegeln, kannst Du jeweils zwei Punkte einer Geraden an der Spiegelachse spiegeln. Bei
Gerade a reicht dafür ein Punkt, da ein Punkt auf der Spiegelachse liegt und auf sich selbst gespiegelt wird.
Beachte bei der Geraden c, dass sie senkrecht zur Spiegelachse steht.
e) Konstruiere zuerst die Spiegelgerade: Dazu verbindest Du die Punkte A und A 0 durch eine Hilfslinie. Bestimme den Mittelpunkt zwischen A und A 0 . Die Spiegelachse steht senkrecht auf der Hilfslinie und verläuft
durch diesen Mittelpunkt. Nun kannst Du den Punkt B an der Achse spiegeln.
14
Freiburger-Verlag.de
Lösungen
3
3. Leitidee Raum und Form
Leitidee Raum und Form
3.1 Dreiecke
a)
I) Konstruktionsbeschreibung: Zuerst zeichnest Du die Basislinie c ein. Dann zeichnest Du um A und B
Kreise, deren Radien die Längen der beiden anderen Seiten sind. An einem der beiden Schnittpunkte der
Kreislinien liegt der Punkt C:
II) Konstruktionsbeschreibung: Zuerst zeichnest Du die Basislinie c. Dann zeichnest Du die Seite b mit
Hilfe des Winkels α = 40◦ ein. Nun zeichnest Du um Punkt B einen Kreis mit einem Radius von 3, 5 cm.
Wo sich der Kreis und die Linie schneiden, liegt der Punkt C.
b) Das Dreiecke I) lässt sich zeichnen.
Dreieck II) lässt sich nicht konstruieren, da es ein gleichschenkliges Dreieck mit einer Winkelsumme größer
als 180 ◦ wäre.
Im Dreieck III) würde die Winkelsumme mehr als 180◦ betragen. Dies kann nicht sein. Also ist es nicht möglich, ein Dreieck zu konstruieren, das den Angaben von III) entspricht.
c)
Ein rechtwinkliges Dreieck kann man so betrachten, dass
eine der beiden Katheten die Höhe auf der anderen Kathete
ist. Dann gilt für den Flächeninhalt: A = a·b
2 .
3.2 Vierecke
a) Zuerst zeichnest Du die Seite a des Parallelogramms. Anschließend wird die Höhe h a und in 1, 5 cm Abstand
eine Parallele zu a konstruiert. Nun zeichnest Du zwei Kreise um Anfangs- und Endpunkt der Seite a mit Radius 2 cm. Die beiden «oberen» Eckpunkte des Parallelogramms erhältst Du als Schnittpunkte der Kreislinien
mit der Parallele – entweder nimmst Du die beiden rechten Schnittpunkte, oder die beiden linken.
Freiburger-Verlag.de
15
3. Leitidee Raum und Form
Lösungen
b) Es ist nicht vorgegeben, welcher Winkel 50◦ betragen soll. Daher kannst Du damit beginnen, eine Linie a zu
zeichnen und eine zweite Linie zu konstruieren, die die erste Linie unter einen Winkel von 50 ◦ schneidet. Nun
brauchst Du nur noch die Länge a auf dieser Linie mit dem Zirkel abzutragen und zwei parallele Linien zu
konstruieren, auf denen Du ebenfalls die Länge a abträgst.
c) Zuerst zeichnest Du die Diagonale d, dann trägst Du die Längen von a und b mit dem Zirkel an beiden Enden
von d ab. Nun brauchst Du nur noch die Schnittpunkte miteinander zu verbinden.
d) Zuerst zeichnest Du die Grundlie a. Anschließend konstruierst Du die Höhe auf dieser Linie. Parallel zu a
konstruierst Du eine Parallele. Nun trägst Du die Längen der Seiten b und d mit dem Zirkel nacheinander auf
der Parallelen ab. An den Schnittpunkten befinden sich die restlichen Eckpunkte des Trapezes.
e)
Ein Viereck ist immer ein Rechteck, wenn
gegenüberliegende Seiten gleich lang sind.
Wenn ich die Fläche eines Parallelogramms
berechnen will, kann ich dazu die Höhe auf
a oder b errichten und erhalte entsprechend
A = a · ha bzw. A = b · hb
16
richtig
falsch
richtig falsch
Gegenbeispiele:
Parallelogramm und Raute
Die Fläche eines Parallelogramms
ist immer «Grundseite mal Höhe».
Bei einer Raute sind alle Winkel gleich
groß.
richtig
falsch
Es sind nur die gegenüberliegenden
Winkel gleich groß:
Bei einem Drachen sind die gegenüberliegenden Winkel gleich groß.
richtig
falsch
Es sind nur zwei gegenüberliegende
Winkel gleich groß:
Freiburger-Verlag.de
Lösungen
f)
3. Leitidee Raum und Form
Es gibt zwei verschiedene Rechenwege:
1. Du berechnest zuerst die Fläche eines Rechtecks
mit den Seitenlängen 4 cm und 5 cm und ziehst
davon das kleine Rechteck rechts ab:
A = 4 cm · 5 cm − 1 cm · 1, 5 cm = 18, 5 cm2
2. Du berechnest die Fläche als Summe aus den
drei Rechtecken «links», «oben» und «unten»:
A = 4 cm · 4 cm + 1 cm · 1 cm + 1 cm · 1, 5 cm
= 16 cm2 + 1 cm2 + 1, 5 cm = 18, 5 cm2
g)
I) Das Element (b − c) · (a − d) ist die Fläches des schraffierten Rechtecks.
II) Du kannst die Fläche der Figur auch so berechnen, dass
Du zuerst den Flächeninhalt des Rechtecks mit den Seiten
a und b berechnest und dann das Rechteck «links oben»
abziehst. Damit ist der Flächeninhalt: A = a · b − c · d.
3.3 Körper
a)
I) Das Volumen des Würfels kannst Du mit der Formel V = a3 berechnen. Also beträgt das Volumen des
Würfels V = (2, 5 cm)3 = 15, 625 cm3. Die Oberfläche beträgt O = 6 · a2 = 6 · (2, 5 cm)2 = 37, 5 cm2
II) Das Volumen des Quaders kannst Du mit der Formel V = a · b · c berechnen. Es beträgt also
V = 2 m · 3 m · 5 m = 30m3 .
Die Oberfläche wird mit der Formel O = 2 · a · b + 2 · a · c + 2 · b · c berechnet. Sie beträgt:
O = 2 · 2 m · 3 m · +2 · 2 m · 5 m + 2 · 3 m · 5 m = 12 m2 + 20 m2 + 30 m2 = 62 m2
b) Wenn die Länge 1 m beträgt, dann beträgt die Breite 2 m und die Höhe 3 m. Das Volumen beträgt damit
V = 1 m · 2 m · 3 m = 6 m3 .
3.4 Achsensymmetrie
a) Um die Symmetrieachsen einzuzeichnen hilft es, wenn Du Dir vorstellst, auf der Symmetrieachse würde
ein Spiegel stehen. Das Spiegelbild muss dann genau mit der zweiten Seite der tatsächlichen Zeichnung
übereinstimmen. Damit erhälst Du folgende Symmetrieachsen:
b) An den Zeichnungen siehst Du, wie viele Symmetrieachsen die einzelnen Figuren besitzen:
c) Die Abbildung b) zeigt alle möglichen Symmetrieachsen. Die zusätzlichen Achsen bei den Abbildungen c)
und d) sind keine Symmetrieachsen.
Freiburger-Verlag.de
17
3. Leitidee Raum und Form
Lösungen
3.5 Spiegelungen
a) Um die Figuren an der angegebenen Achse zu spiegeln, gehst Du wie bei den Beispielen vor: Du spiegelst die
Ecken an der Achse. Im Fall des Rechtecks rechts, kommt es dabei sogar zu einer Überlappung:
b) Um die Spiegelachsen zu bestimmen, verbindest Du zuerst sich entsprechende Ecken miteinander. Dann halbierst Du die so entstandenen Strecken. Durch die Mittelpunkte kannst Du dann die Spiegelachse s zeichnen:
18
c)
Du kannst ein beliebiges Dreieck wählen.
Der Umlaufsinn der Punkte dreht sich um,
wenn einmal gespiegelt wird. Nach der zweiten Spiegelung dreht er sich wieder um. Also
besitzt das dritte Dreieck wieder den gleichen
Umlaufsinn wie das erste Dreieck.
d)
Um die Geraden zu spiegeln, ist es am einfachsten, je zwei Punkte zu spiegeln. Es entsteht folgende Figur:
e)
Zuerst musst Du die Spiegelachse bestimmen.
Dazu verbindest Du die Punkte A und A 0
und bestimmst den Mittelpunkt M der Verbindungslinie. Durch diesen Punkt kannst Du
nun die Spiegelachse s konstruieren, die senkrecht auf der Verbindungslinie stehen muss.
Nun kannst Du den Punkt B spiegeln.
Freiburger-Verlag.de