Kosmologie Kapitel 11

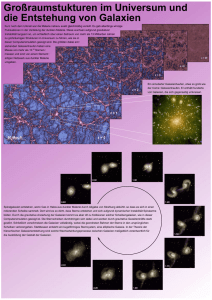
11. Bildung von Strukturen.
Fig. 11.1 2dF-Programm. Die inhomogenen Verteilung von mehr als 63000 Galaxien
und deren Rotverschiebung wurde in einem scheibenförmigen Sektor gemessen. Das
Ganze besteht aus zwei 4°-Ausschnitte aus einer Gesamtmenge von 210 000
Galaxien.
11.1. Dichtekonstrast im linearen hydrodynamischen Modell
Die Verteilung der leuchtenden Materie im heutigen Kosmos ist sehr
ungleichmäßig. Neben Sternen gibt es Sternassoziationen, Sternhaufen,
Galaxien. Diese wieder bilden Galaxienhaufen (s. Fig. 11.1), die wieder in
Superhaufen zusammenhängen und durch riesige Hohlräume voneinander
getrennt sind. Es ist die Frage, die uns in diesem Kapitel beschäftigen wird, wie
denn aus den Fluktuationen der Hintergrundstrahlung (s. z.B. Fig. 9.4 und 9.7),
deren relative Amplitude δT = ∆T / T ≈ 10 −5 nur eine winzige Abweichung von
der Homogenität darstellt, die heutigen Strukturen und ihre Hierarchien
entstanden sind. Wir interessieren und dabei für den Dichtekontrast
r
r ρ( x ) − ρ
δ( x ) =
ρ
129
(11.1)
Er hängt mit der Temperaturfluktuation (CMB) wie folgt zusammen
r
r
∆T ( x )
δ( x ) = 3 ⋅
T
(11.1a)
Anstelle der Dichtestörung im x-Raum wird häufig deren FourierTransformierte benutzt
r 1
r
r
δ k = ∫ δ( x )exp ikx ⋅ d 3 x
(11.2)
V
()
wobei V das Volumen bedeutet. Fig. 11.2 zeigt eine eindrucksvolle Darstellung
δ(r )
und
den
entsprechenden
der
heutigen
Kenntnis
von
Beobachtungsmethoden.
Fig. 11.2. Dichtefluktuationen δ(r ) , zusammengestellt vom Team des „Sloan Digital Sky
Survey“ (SDSS). Die Beobachtungen beziehen sich auf CMB, die Häufigkeit von
Galaxien-Cluster (gut im Röntgengebiet durch die Strahlung des heißen
intergalaktischen Gases zu beobachten), die Auswertungen von SDSS, die Häufigkeit
von Gravitationslinseneffekten und der intergalaktische neutrale Wasserstoff,
beobachtet als Lyman-Alpha-Wald. Nach Max Tegmark’s Cosmological Library.
http:/www.hep.upenn.edu/~max/2df1.html
130
Die Entfernungsskala in Fig. 11.2 kann auch als Zeitskala interpretiert werden.
Es sind Eigenabstände, also Entfernungen bezogen auf den heutigen Kosmos,
wobei die Grenze durch den Teilchenhorizont d H = 3ct 0 ≈ 40 ⋅ 10 9 Lj gegeben
ist. Neben dem Dichtekontrast wird häufig auch die Streuung angegeben
δ( x ) = σ 2 = konst.
2
(11.3)
Im k-Raum erhält man das Leistungsspektrum
δ(k )
2
≡ P (k )
(11.4)
was mit σ 2 auf folgende Weise zusammenhängt
σ2 =
V
P(k )d 3 k
3 ∫
(2π )
(11.5)
Die Größen in eckigen Klammern sind Mittelbildungen über das Ensemble.
r
Um die zeitliche Entwicklung kleiner Störungen zu untersuchen δ( x , t ) ≡ δ , kann
man aus den hydrodynamischen Gleichungen eine Wellengleichung ableiten,
welche in einem stationären Medium die Form annimmt
−
1 &&
δ + ∇ 2 δ = 4πG ρ
2
cS
(11.6)
wobei ρ ≡ ρ ist. Gl. 11.6 unterscheidet sich von der Wellengleichung in der
Elektrodynamik durch das Glied auf der rechten Seite, dass die Selbstgravitation
der Materie beschreibt. Setzt man die Wellenlösung ein
[(
rr
δ ∝ exp i k x − ωt
)]
(11.7)
so erhält als Fourier-Transformierte von Gl. 11.6 eine Dispersionsbeziehung
ω2 = k 2 c S2 − 4πG ρ = cS2 (k 2 − k J2 )
(11.8)
mit der so genannten Jeans-Wellenzahl
 4πG ρ 
k J =  2 
 cS 
und der Jeans-Masse
131
1
2
(11.9)
4π  π
M J = 
3  kJ
3

 ρ

(11.10)
Wellenausbreitung ist nur möglich, wenn k > k J ist. Für k < k J ist ω2 < 0 . Es
gibt keine laufende Welle mehr, stattdessen zwei Lösungen, eine exponentiell
wachsende und eine exponentiell abklingende.
Die Situation ändert sich, wenn man die kosmische Expansion berücksichtigt.
Dazu setzt man
x′
(11.11)
x=
a
und erhält unter Vernachlässigung von Druckkräften
2 2
&δ& + 2 Hδ& + cS k − 3 ΩH 2 δ = 0
R2
2
(11.12)
wobei wir unter Benutzung der Friedmann-Gleichung
8πG ρ = 3H 2 Ω
(11.13)
gesetzt haben. Für ein Universum mit Ω = 1 ( R → ∞) gibt es jetzt zwei
Lösungen
r
r
δ( x , t ) = D± (t ) ⋅ δ( x )
(11.14)
mit
D+ (t ) = A ⋅ t
2
3
∝ a (t ) und D− (t ) = B ⋅ t −1
(11.15)
Die Expansion scheint das Wachsen (und Abklingen) der Störung zu behindern,
denn anstelle eines exponentiellen Wachstums (oder Abklingens) mit Gl. 11.7
und 11.8 ergibt sich ein moderates Potenzgesetz.
Wir können das Verhalten der Jeans-Masse für Baryonen untersuchen, wenn wir
k J = k J′ / a schreiben. Es ist nach Gl. 11.10
M J ∝ ρ . In der
strahlungsdominierten Epoche ist ρ ∝ T 4 . Andererseits ist k J ∝ T 2 (Gl. 11.6).
Also wird mit Gl. 11.7 M J ∝ T −3 . In Fig. 11.3 ist der Übergang von der
strahlungsdominierten zur materiedominierten Epoche abrupt eingezeichnet.
Dabei fällt die Schallgeschwindigkeit von c S = c / 3 = 1,7 ⋅ 10 8 m/s auf
c 2 S = 5 / 3 ⋅ k B T / µm P und c S = 4,7 ⋅ 10 3 m/s ab, was zu einem Absinken der
132
Jeansmasse um viele Zehnerpotenzen führt ( mP Protonenmasse, µ mittlere
Massenzahl pro Teilchen).
Fig. 11.3. Jeans-Masse der Baryonen MB-J und die Baryonen-Masse innerhalb des
Horizonts MB-HOR. MS ist die Silkmasse, s. dazu den Text. Als baryonische Dichte wurde
Ω B h 2 = 0,047 angenommen. Nach E.W. Kolb, M.S. Turner : The Early Universe.
Addison Wesley 1990.
Sie liegt vor der Rekombination zwischen 1014 und 1018 Sonnenmassen, was an
der unteren Grenze etwa der Größe von Galaxienhaufen entspricht. Unmittelbar
nach der Rekombination ( z ≈ 1090 ) liegt sie jedoch bei ca. 106 Sonnenmassen,
das ist etwa die Größe eines Kugelsternhaufens. Auch Dämpfungseffekte
können in der strahlungsdominierten Epoche eine Rolle spielen. Sie wurden von
J. Silk zuerst behandelt und in Fig. 11.3 als „Silkmasse“, MS, eingetragen. Es
muss aber festgestellt werden, dass keine Massen die Entstehung von Galaxien
erklären kann.
Außerdem kann man leicht zeigen, dass die Entwicklung eines Dichtekontrastes
mit baryonischer Materie völlig unzureichend ist. Wir gehen zur Zeit der
r
Rekombination von einem Dichtekontrast δ( x , t rec ) ≈ 5 ⋅ 10 −5 aus. Nach
Gl. 11.15 wird dann der Wert in der Gegenwart
r
r
δ( x , t 0 ) ≈ δ( x , t rec ) ⋅ ( z rec + 1) ≈ 10 −2
r
Benötigt wird aber ein δ( x , t 0 ) ≈ 1 , damit ein Gravitationskollaps einer Gaswolke
einsetzt. Wenn wir für die Zeit, in der sich Galaxien bilden, z = 10 einsetzt, wird
das Ergebnis noch um eine Größenordnung kleiner. Man sieht hier schon, dass
während der Expansion nach dem Standardmodell die Baryonen allein den
Kontrast nicht genügend verstärken können. Dunkle Materie muss
133
hinzukommen. Diese breiten sich stoßfrei und ohne Dissipation der Energie aus.
Baryonische Materie dagegen kann kinetische Energie durch Abstrahlung
verlieren. In einer Wolke aus dunkler und baryonischer Materie wird sich die
baryonische unter Verlust von kinetischer Energie und Drehimpuls in das Innere
der Wolke bewegen. Es kann daher dort leicht ein ausreichenden Dichtekontrast
entstehen. Die dunkle Materie bildet dagegen einen nahezu stationären
Potentialtopf, in welchem die baryonische Materie einer Galaxie eingeschlossen
ist.
Man kann auch für eine dunkle, stoßfreie fermionische Materie eine maximale
Jeansmasse ableiten. Doch diese ist abhängig von der Masse der Teilchen der
dunklen Energie. Da eben diese noch völlig unbekannt ist, scheint mit diesen
Überlegungen wenig gewonnen zu sein (s. z.B. G. Börner: The Early Universe.
4th Edition Ch. 10.2.2.).
Fig. 11.4. Ein Bild-Komposit des „Bullet Cluster“. Die Galaxien des Cluster sind als
diffuse weiße Flecken zu sehen. Das fast 10fache Masse der leuchtenden baryonischen
Materie besitzt die rot dargestellte Wolke aus intergalaktischen Materie (IGM), welche
im Lichte der emittierten Röntgenstrahlung (Chandra) zu sehen ist. Schließlich stellt die
blaue Wolke die Verteilung der dunklen Materie dar, die durch „Scannen“ mittels des
Gravitationslinseneffektes bestimmt wurde. Ihre Masse überwiegt die der baryonischen
Materie um etwa einen Faktor 7. Quelle der Aufnahme X-ray: NASA/CXC/CfA/
M. Markkevitsch et al. Lensing: NASA/STScI, ESO WFI, Magellan/U. Arizona/D.Clowe
et al. Optical: NASA/STScI, Magellan/U. Arizona/D.Clowe et al. 2006
In Fig. 11.4 ist ein jüngst publiziertes Beispiel zu sehen, wo sich im Innern einer
großen Wolke dunkler Materie viele Galaxien befinden. Man geht davon aus,
134
dass die Galaxien oder Protogalaxien alle ihr Halo aus dunkler Materie
mitbringen und dass im Laufe der Zeit weitere Vereinigungen zu größeren
Strukturen ganz wesentlich von den Halos der dunklen Materie bestimmt
werden. Während heftiger Sternbildung kommt es häufig zu SupernovaExplosionen, bei welchen große Mengen heißer Gase (d.h. H, He und geringe
Mengen schwerer Elemente) in den intergalaktischen Raum ausgeschleudert
werden.
11.2. Die weitere Entwicklung des Dichtekontrasts. Das sphärische
Kollapsmodell.
In der von Materie dominierten Epoche wächst δ( x ) rasch an, so dass einer
linearen Behandlung nicht mehr vertraut werden kann. Wir benutzen hier
stattdessen ein sphärisches Kollaps-Modell (s. dazu A.R. Liddle, D.H. Lyth :
Cosmological Inflation and Large-Scale Structure, Chap. 11. Cambridge Univ.
Press 2000). Im nichtlinearen Bereich betten wir in das Universum mit kritischer
Dichte, ( Ω = 1) , ein sphärisches Volumen mit einer „Überdichte“ Ω = 1 + δ > 1
ein.
Fig. 11.5. Entwicklung des Skalenfaktors. Untere Kurve für Ω 0 = 1 + δ exakt
gerechnet. Mittlere Kurve für Ω 0 = 1 + δ in linearer Näherung. Obere Kurve für
Ω 0 = 1 (kritische Massendichte des Hintergrunds). Nach A.R. Liddle, D.H. Lyth :
Cosmological Inflation and Large-Scale Structure. Cambridge Univ. Press 2000.
Das Gebiet außerhalb entwickelt sich wie ein Universum mit kritischer Dichte.
Dagegen gelten jetzt für das kollabierende Gebiet Ω > 1 die beiden Gleichungen
2.21
a(t ) 1 Ω
=
(1 − cos θ)
a (t 0 ) 2 Ω − 1
135
(11.13)
H 0t =
1
Ω
(θ − sin θ)
2 (Ω − 1)3 2
(11.14)
Die Funktion Gl. 11.13 erreicht ein Maximum bei θ = π , daher können wir Gl.
11.13 und 11.14 in amax und t max ausdrücken (was in Fig. 11.5 untere Kurve als
„non-linear“ dargestellt ist)
a(t ) 1
t
1
= (1 − cos θ ) und
= (θ − sin θ )
a max 2
t max π
(11.15)
Um Gl. 11.15 auch im linearen Bereich zu untersuchen, entwickeln wir bis zur
zweiten Ordnung
t
a(t ) θ 2 θ 4
1  θ3 θ5 

≅
−
und
≅  −
4 48
t max π  6 120 
a max
(11.16)
Setzen wir t in a(t) ein, so erhalten wir in „linearer“ Näherung
alin (t ) 1 
t 

≅  6π
a max
4  t max 
2
3
2

3


1
t

 
⋅ 1 −  6π
20
t



max 


(11.17)
Diese Funktion wird in Fig. 11.4 durch die mittlere Kurve (linear) dargestellt. In
Gl. 11.17 beschreibt der erste Faktor auf der rechten Seite den kritischen Fall
Ω = 1 und entspricht damit Gl. 2.20. Wir nehmen an, dass der Skalenfaktor des
Hintergrunds dem kritischen Fall, also der euklidischen Geometrie im Materie
dominierten Universum entspricht, siehe obere Kurve „background“ in Fig.
11.4. Wir können jetzt den Dichtekonstrast für verschiedene
Entwicklungsstadien ausrechnen. Wie verhält sich z.B. der lineare
Dichtekonstrast
3
aback
ρlin
1 + δ lin =
= 3
(11.18)
alin
ρ back
Der letzte Ausdruck auf der rechten Seite von Gl. 11.18 läßt sich aus Gl. 11.17
gewinnen, indem wir zunächst beachten dass der erste Faktor auf der rechten
Seite von Gl. 11.17 die Entwicklung des Hintergrundes beschreibt und zur 3.
Potenz im Zähler und im Nenner von 11.18 auftritt, d.h. er kann gekürzt werden.
Es bleibt die eckige Klammer aus dem Nenner stehen mit dem folgenden
Ergebnis
136
−3
2
2
1 − 1 (6π t
) 3  ≈ 1 + 3 (6π t
) 3  ≈ 1 + δ lin ,
t max 
t max 
20
20


und
t 
3

δ lin =  6π
20  t max 
2
3
(11.19)
Dieser Ausdruck wird am Umkehrpunkt, bei t = t max
δ lin (t max ) =
2
3
(6π ) 3 = 1,06
20
(11.20)
Der Dichtekontrast ist also praktisch „1“, wenn bei der nichtlinearen Lösung der
Umkehrpunkt zum Kollaps erreicht ist. Das ist auch die Grenze der
Anwendbarkeit der linearen Näherung. Am Endpunkt des Kollaps, bei t = 2t max
ist der Dichtekonstrast in der linearen Theorie
2
3
δ lin (2t max ) = (12π ) 3 = 1,686
(11.21)
20
Interessanter ist es, jetzt 1 + δ(tmax) in der nichtlinearen Theorie ausrechnen
3
Der Nenner ergibt nach Gl. 11.15 „eins“, so dass nur aback
im Zähler etwas
beiträgt
3
aback
(6π )
1 + δ(t max ) = 3 = 3 = 5,55
4
amax
2
(11.22)
Damit ist der Dichtekonstrast über 4-mal so groß wie in der linearen Theorie. Es
ist nicht realistisch jetzt den Fall t = 2t max zu untersuchen, denn die Dichte
divergiert. Wir können uns aber vorstellen, daß zu Beginn eine Masse M der
Ausdehnung R im wesentlichen potentielle Energie besitzt
E ges ≈ E pot
GM 2
=α
R
(11.23)
Hier ist α ein Faktor von der Größenordnung „1“. Der Kollaps heizt die Materie
auf, ihre thermische (oder kinetische ) Energie verhindert zunächst den weiteren
Kollaps. Man spricht von Virialisierung, wenn sich stabile, zeitlich konstante
Mittelwerte der potentiellen und kinetischen Energie eingestellt haben. Dann ist
E ges =
1
E pot
2
137
(11.24)
und wenn die Gesamtenergie ungefähr konstant geblieben ist, wird
RVir ≈
R
2
(11.25)
Damit wäre die Virialisierung abgeschlossen. Wir wollen hier nicht
berücksichtigen, dass die kollabierende Wolke im Infraroten Strahlungsenergie
abgibt. Stattdessen berücksichtigen wir die Virialisierung indem wir a und aback
bei t = 1,82 tmax berechnen, wenn a/amax auf ½ gefallen ist. Das Ergebnis ist
 a(1,82 ) 
1 + δ(vir ) = 
 = 157
 0,5 
3
(11.26)
Der Wert für den Dichtekonstrast bei abgeschlossener Virialisierung, den man
aus numerischer Simulation gewinnt, liegt bei 178. Bei Annahme eines
Universums mit Ω M und Ω Λ = 1 − Ω M erhält man näherungsweise
1 + δ(vir ) ≅ 157 ⋅ Ω −M0, 6 .
(11.27)
Fig. 11.6. Einbringen von Glasfasersträngen in die Brennebene des 2,5m Teleskops des
„Sloan Digital Sky Survey„ (Kitts Peak Observatory).
138
11.3. Katalogisierungen von Galaxien und Galaxienhaufen
Fig. 11.7. Ein 2,5° Ausschnitt mit 24 915 Galaxien aus der SDSS-Durchmusterung. Der
äußere Kreis entspricht z = 0,2. Aus V.J. Martinez & E. Saar : Statistics in Cosmology.
SPIE Proceedings Vol. 4847, 2002, Astronomical Data Analysis. J.L. Stark and F.
Murtagh, eds.
Die empirische Untersuchung des Dichtekontrasts bezieht sich auf umfangreiche
Kataloge von Galaxien, deren Position und Rotverschiebung. Moderne MultiGlasfaser-Techniken ermöglichen es gegenwärtig, 70 – 2000 Rotverschiebungen
von Galaxien pro Nacht spektroskopisch zu vermessen, während es vor
Einführung dieser Technik nur 5 – 10 waren. Die Grenz-Größenklasse im blauen
Spektralbereich stieg von 14 auf 19,5, ein Fortschritt der nicht nur größeren
Teleskopen sondern vor allem auch dem Einsatz von CCD-Platten, den
elektronischen Fotoplatten (s. Fig. 11.5), zu verdanken ist. Zwei zur Zeit
laufende große Projekte sind das 2dF (2 degree field) und der SDSS (Sloan
Digital Sky Survey). Die SDSS-Durchmusterung ist z.Zt. die umfangreichste.
Sie wird in 5 Wellenlängenbereichen mit einer Mosaik-CCD-Kamera
durchgeführt. Die Photometrie erreicht dabei Objekte bis 23. Größe, die Analyse
der Rotverschiebung reicht bis zur Größe 17,7. Diese Untersuchungen sind nicht
nur für die Massenverteilung von großem Interesse, sondern auch für das
Verständnis der Entwicklung morphologischer Merkmale. Jede Galaxie wird
durch 3 Angaben charakterisiert: Position ( α, δ, r = comoving distance), n (r ) =
r
radiale Selektionsfunktion, n (rˆ ) = Winkelselektionsfunktion mit rˆ = r / r . Der
gesamte untersuchte Raumwinkel beträgt 2499 Quadratgrad.
139
Das zweite Großprojekt ist der „Anglo-Australian 2dF Galaxy Redshift Survey“
(Mt. Stromlo Observatory). Im Jahr 2001 wurden die ersten 105 Galaxien des
Südhimmels mit Rotverschiebungen publiziert (M. Colless et al. : MNRAS 328,
1039, 2001). Die Objekte sind heller als Größe 19,5. Das untersuchte Gebiet
umfasst 2000 Quadratgrad und erreicht z = 0,2 ( ca. 600 h-1 Mpc). Man rechnet
bei Beendigung des Projekts mit 250 000 Galaxien, deren Position und
Rotverschiebung vermessen wurden.
Fig.11.8. Fornax Cluster im Röntgenlicht, gemessen von Chandra bei 1 keV.
Credit: NASA /CXC/Columbia U./C.Scharf et al. 2004
Die Verteilung der Galaxiencluster kann am besten an Hand ihrer
Röntgenbremsstrahlung untersucht werden, wobei die Energie bei 1 – 10 keV
liegt. Diese Methode hat sich auch als der beste Weg erwiesen, große,
homogene Cluster zu identifizieren. und wurde im Projekt REFLEX (ROSATESO Flux Limited X-ray) bis zum Jahre 2002 auf 452 Cluster angewandt. Durch
Messung des Röntgenspektrums kann man aus der Temperatur des heißen (und
sehr dünnen) Plasmas direkt die Masse bestimmen. Man geht dabei vom
Virialsatz aus
3
1 Gµm P M vir 1
= µmP σ 2υ
k BT =
2
2
r
2
(11.28)
wobei mP die Protonenmasse, µ die mittlere Massenzahl der Teilchen (µ ≅ 0,6),
2
σ 2υ = 3 υ r die Geschwindigkeits-Dispersion der Galaxien in radialer Richtung
und Mvir die Virialmasse des Clusters bedeuten.
140
Fig. 11.9. Räumliche Verteilung der „X-ray Cluster“ des REFLEX Survey. Jeder Punkt
stellt einen Galaxienhaufen mit hunderten bis tausenden Galaxien dar. Kettenartige
Strukturen sind zu erkennen. Nach s. Borgani, L. Guzzo : Nature 410, 169, (2001).
Die Intensität der Röntgenstrahlung verhält sich zur Dichte n des Plasmas und
der Temperatur T wie
I X ∝ n 2T
1
2
(11.29)
Da die optische Intensität nur mit dem Quadrat von n geht, folgt, dass IX für
diesen Zweck einen wesentlich besseren Kontrast erwarten lässt als optische
Untersuchungen. Unter Zugrundelegung eines Dichteprofils kann man den
Massenanteil des Plasmas bestimmen. Die ermittelte Clustermasse umfaßt die
Gesamtmasse, d.h. dunkle Materie und baryonische Masse. Dabei ist der Anteil
des heißen intergalaktischen Plasmas an der Gesamtmasse gleich f gas = 0,113 ,
dabei aber um etwa einen Faktor 6 größer als die optisch leuchtende Masse der
Galaxien (s. S.W. Allen et al. astro-ph/0205007).
Schließlich sei noch der „IRAS Point Source Catalogue (PSC) Redshift Survey“
erwähnt, der 24 500 Galaxien enthält, bei 60 µm über 84% des Himmels abdeckt
und alle Punktquellen mit einem Fluß ≥ 1,2 Jansky einschließt. Von IRAS PSC
sind Leistungsspektren P(k) publiziert worden (s. W. Sutherland et al. astroph/9901189), auf die wir später noch zurückkommen werden.
141
11.4. Leistungsspektren der Massenverteilung
Fig. 11.10. Links (unten): Leistungsspektren P(k ) von je 147 000 2dF-Galaxien und
105 SDSS-Galaxien, (oben) P(k ) von REFLEX-Cluster. Rechts: ZweipunktKorrelationsfunktionen ξ(r ) von 2dF- , SDSS- und Las Campanas-Galaxien
Für einen Vergleich mit Modellen wird das Leistungsspektrum P(k ) (s. Gl. 11.2
r
und 11.4) dem Dichtekontrast δ( x ) (Gl. 11.2 und Fig. 11.2) vorgezogen. Man
kann das Leistungsspektrum durch ein Potenzgesetz annähern
P(k ) = A ⋅ k n
Im Bereich sehrgroßer Raumdimensionen (kleiner k-Werte) nähert sich
n ≈ 1 (aus Fluktuation des CMB). Für kleine Raumdimensionen (große k-Werte)
wird n ≈ −1,8 . Den entsprechenden Übergangsbereich liefert bei den
berechneten Kurven nur das „Cold Dark Matter“(CDM-)Modell. In Fig. 11.8
sind links Leistungsspektren P(k ) aufgetragen. Sie fallen mit steigendem k (d.h.
mit abnehmender Wellenlänge) ab. Die durchgezogenen Linien suggerieren bei
300 h-1 Mpc ein Maximum, die aufgetragenen Punkt scheinen eher einem
Sättigungswert zu zustreben. In Fig. 11.11 ist das Leistungsspektrum von IRASGalaxien aufgetragen. Sie überdecken einen größeren Raumbereich. Hier ist
eher die Andeutung eines Maximums zu sehen. Bei der Normierung der P(k ) Kurven muss beachtet werden, dass die leuchtende Materie der Galaxien nur
einen Bruchteil von etwa 0,005 der Gesamtmasse ausmacht. Man definiert
deshalb zur Normierung einen Bias-Faktor
b2 =
PGal (k )
PM (k )
(11.30)
142
Fig. 11.11. Transferfunktion für ein „Cold Dark Matter“ (CDM) Model für die
Parameter Γ = 0,5; 0,4; 0,3; 0,2. Die heutigen Konkordanz–Werte ergeben Γ = 0,17 .
Nach J.M. Bardeen et al. ApJ 304, 15 (1986).
Geht man von einer Störung δ(k, t rec ) zur Zeit der Rekombination trec aus, dann
wird eine Transferfunktion im Rahmen der linearen Theorie angesetzt, welche
die Entwicklung der Störung zu einer späteren Zeit beschreibt
δ(k , t ) = T (k , t ) ⋅ δ(k , t rec )
(11.31)
Fig. 11.11 gibt ein Beispiel. Die Transferfunktion gilt für die gegenwärtige
Beobachtung und ist für ein „Cold Dark Matter“ (CDM) Model berechnet. Die
Abhängigkeit von der Wellenzahl wird qualitativ richtig dargestellt. Bei kleinen
Wellenzahlen, d.h. großen Skalen nimmt T (k ) den Wert eins an, weil das
ursprüngliche Leistungsspektrum durch CDM-Teilchen nicht gestört wird; d.h.
das Leistungsspektrum, wie es in der Rekombination-Phase vorliegt, ist kunabhängig, wie von der Inflation gefordert (Gl. 10.6 und 10.7). Die
Transferfunktion in Fig. 11.9 wird als Funktion T (q ) einer normierten
Wellenzahl q angegeben, wobei
k
q=
(11.32)
hΓ
Der „Shape Parameter“ ist wie folgt definiert
(
Γ =Ω M h exp − Ω B − 2hΩ B / Ω M
)
(11.33)
Mit den gegenwärtig bevorzugten Werten (Concordance Model) wird Γ ≅ 0,17 .
143
Fig. 11.12. Das Leistungsspektrum P(k ) der IRAS-Galaxien (1,2 Jy) im Vergleich zu
anderen Durchmusterungen. Gestrichelt ist das Ergebnis einer linearen CDM-Theorie
für Γ = 0,2 und 0,5 sowie σ8 = 0,8 eingetragen.
Bei der Berechnung von P(k ) aus den Meßdaten muß berücksichtigt werden,
daß im Gegensatz zur mathematischen Fouriertransformation, welche die
Integration über einen unendlichen Raum erfordern, die Beobachtung immer nur
ein endliches Raumelement überdeckt. Deshalb müssen Fensterfunktionen im kRaum angesetzt werden, deren Effekt sorgfältig getestet werden muß.
11.5. N-Teilchen-Simulationen
Erst in den letzten Jahren sind P(k ) -Auftragungen, die aus Beobachtungen
gewonnen wurden, genau genug, um daran theoretische Modell zu testen. Das
„Hot Dark Matter Model“ (HDM) hat dabei nur noch historische Bedeutung.
Eine wichtige und testbare Vorhersage des Modells, war eine Entwicklung von
großen zu kleinen Strukturen (top down model), welche von den Beobachtungen
nicht gestützt wird. Das HDM wurde in den 80er Jahren von dem „Cold Dark
Matter Model“ (CDM) abgelöst, das eine Entwicklung von kleinen zu großen
Strukturen vorhersagt, was sehr viel besser mit den Beobachtungen
übereinstimmt. Aus dem CDM entwickelte sich ein „Standard Cold Dark Matter
Model“ (SCDM) mit den Parametern Ω 0 = 1 , h = 0,5 (Hubble Konstante in
Einheiten von 100 km/s⋅Mpc), n = 1 (Harrison-Zeldowich-Spektrum) und b =
1,5 – 2,5. Das SCDM konnte ausgeschlossen werden, da es die gemessenen
Spektren nur unzureichend wiedergibt. So wird die Haufenbildung von Galaxien
144
über größere Skalen beobachtet, als aus dem SCDM hervorgeht. Eine
Alternative ist das Open Cold Dark Matter Model OCDM mit Ω 0 < 1. Es
Fig.
11.13. Simulationsergebnisse zu den unten im Text beschriebene Modellen.
vergrößert den Horizont zur Zeit der Gleichheit von Materie und Strahlung,
wodurch vermehrte Haufenbildung auf großen Skalen auftritt. In einem anderen
Modell wird, unter Beibehaltung von Ω 0 = 1 , Ω M = 0,2 gesetzt, so dass
145
Ω Λ = 1 − Ω M wird. Dieses Modell wird „Λ Cold Dark Matter Model“ (ΛCDM)
genannt, wobei der größte Einfluß auf P(k ) von Ω M kommt, während Ω Λ kaum
beiträgt. Wenn stattdessen der Anteil relativistischer (heißer) Materie erhöht
wird, schafft man einen ähnlichen Effekt. Dieses Modell wird τCDM gernannt.
Unter dem Eindruck der Ergebnisse des WMAP-Projekts spricht man in jüngster
Zeit vom „Concordance Model“ mit Parametern wie Ω M = 0,3 , h = 0,7 .
Fig. 11.14. Ergebnisse der „Milleniums-Simulation, einer der größten bisher
durchgeführten N-Teilchen Simulationsrechnung mit mehr als 1010 Teilchen
Dargestellt ist die Entwicklung der Materieverteilung (dunkle Materie) in der
Gegenwart 13,7 Gigajahre nach dem Big Bang. Das untere Bild zeigt das gleich
Ergebnis wie oben aber mit mehr als 10-facher linearer Vergrößerung (nach Volker
Springel, MPI f. Astrophysik Garching).
146
Es muss noch einmal betont werden, dass die Strukturen, welche sich bei den
Simulationen ergeben, aus dunkler Materie bestehen. Diese bilden Bereiche
eines niedrigeren Gravitationspotentials, in welchen sich baryonische Materie
sammelt. Offen ist noch die Frage, ob in Ω M nicht auch noch heiße dunkle
Materie verborgen ist, z.B. „schwere“ Neutrinos (µ- und τ-Neutrinos). Es ist
möglich, dass diese Frage in den nächsten Jahren durch Präzisionsmessungen
der Hintergrundstrahlung mit dem PLANCK-Satelliten der ESA gelöst werden
kann. Die Modellrechnungen werden einerseits mit N-Teilchen-Simulationen
durchgeführt, andererseits mit semianalytischen Methoden. Die umfangreichsten
N-Teilchen-Simulationen werden z. Zt. vom Virgo-Team vorangetrieben, an
welchem auch das MPI f. Astrophysik in Garching beteiligt ist. Das Model
LCDM geht von den Werten Ω M = 0,3 , Ω L = 0,7 , h = 0,7 und σ8 = 0,9 aus. σ8
ist die Streuung in einem Würfel der Kantenlänge r = 8/h Mpc. Der in den
Modellen simulierte Würfel hat eine Länge von 3000/h Mpc mit 109
Massenelementen. Die Simulation beginnt bei z = 35.
Fig. 11.13 zeigt das Ergebnis einer der umfangreichsten Modellrechnungen mit
den Parametern des Konkordanzmodells.
Zu den semianalytischen Modellen muß auf die Literatur verwiesen werden.
Hinweise finden sich L. Guzzo : Large-Scale Structure from Galaxy to Cluster
Surveys. Review in DARK2002, 4th Heidelberg Conf. On Dark Matter in Astroand Particle Physics. H.-V. Klapdor-Kleingrothaus & R. Viollier eds. Springer
2002. H.J. Mo, S. Mao, S.D.M. White: The formation of galactic disks. MNRS
295 (1998) 319
11.6.
Weitere Meßmethoden zur Massenverteilung
Machen wir uns noch einmal klar : Nur 4% der Masse des Univesums ist
baryonische Masse. 96% sind Materie- bzw. Energieformen, die uns noch völlig
unbekannt sind. Diese Feststellung ist so ungeheuerlich, daß von Seiten der
Beobachtung alles getan werden muß, das Ergebnis Ω B = 0,04 , Ω M = 0,3 ,
Ω Λ = 0,7 abzusichern. Das kann vor allem durch möglichst viele verschiedene,
völlig unabhängige Meßverfahren geschehen. Wir wollen hier einige neue
Verfahren kurz erwähnen, deren Anwendung sich noch in den Anfängen
befindet, deren Bedeutung in Zukunft aber sehr wahrscheinlich zunehmen wird.
11.5.1.
Der Sunyaev-Zeldovich-Effekt (SZE) beschreibt inverse
Comptonstreuung von Photonen des CMB an heißen Elektronen des
intergalaktischen Plasmas in Galaxienhaufen. Damit kann die
Massenverteilung der Cluster untersucht werden. Solche Untersuchungen
wurden bei 150, 210 und 275 GHz mit einem Bolometer-Array am ViperTeleskop gemacht, das am Südpol aufgestellt ist. Die 3 Frequenzkanäle
gestatten es, die spektrale Verschiebung des CMB-Spektrums zu höheren
147
Frequenzen zu detektieren. Mit der hier zitierten Messung wurden u.a.
zwei Cluster untersucht, welche im REFLEX-Katalog die größte
Röntgen-Helligkeit besitzen: Abell S 1063 (z = 0,347) und 1E 0657-67 (z
= 0,299). Fig. 11.12 zeigt die Ergebnisse von 1E 0657-67. Die Effekte
erfordern eine hohe Empfindlichkeit der Messung, die z.Zt. knapp erreicht
wird. Der SZE fürht zu einer völlig unabhängigen Bestimmung von
Cluster-Morphologien und Massen.
Gravitationslinsen-Effekte hängen i.a. von der dunklen Energie und
11.5.2.
im Detail von der Massenverteilung großer Galaxien ab, die für entfernte
Galaxien und Quasare als Linsen wirken. Man unterscheidet normale
Linseneffekte, d.h. Ablenkungen im Bereich von Bogensekunden, und
Weitwinkelaufspaltungen ( ∆θ ≥ 4" ), wobei diese sehr empfindlich auf
Dichteverteilungen ansprechen. Auf der Grundlage der bisher
beobachteten Systeme lassen sich die verschiedenen Effekte noch nicht
trennen.
Fig. 11.15. Farbcodierte Bilder der CMB-Temperaturen des Galaxienhaufens 1E065767. Die darüberliegenden weißen Konturen sind ROSAT-Messungen. Der
Strahldurchmesser des ACBAR –Mikrowellen-Teleskops beträgt 4,5 Bogenminuten. Die
Farbcodierung umfaßt den Temperatur-Bereich von –200 bis +200 µK. Nach P. Gomez
et al. astro-ph/0311263.
148
Das
sollte
aber
mit
einer
größeren
Ansammlung
von
Beobachtungsmaterial möglich sein. Gravitationslinsen bieten eine
interessante unabhängige Methode, die dunkle Energie zu untersuchen,
deren Größe bis jetzt im Wesentlichen aus SN Ia-Beobachtungen und in
jüngster Zeit aus den von WMAP mit großer Genauigkeit gemessenen
Fluktuations-Spektrum des CMB bestimmt wurde.
11.5.3. Neben der Hubble-Fluchtgeschwindigkeit besitzen alle Galaxien auch
noch Eigenbewegungen. Ihre Geschwindigkeit oder genauer deren
radiale Komponente wird als störender Effekt immer mitgemessen, wenn
Rotverschiebungen bestimmt werden. Die Eigenbewegungen (auch
Pekuliarbewegungen genannt), zeigen Beschleunigungen in
Gravitationsfeldern an. Damit enthalten sie wichtige Informationen über
Ω M im allgemeinen und über die Massenverteilung in Galaxienhaufen
im Speziellen. Zur Bestimmung der Pekuliarbewegungen werden die
Daten aus Galaxienkataloge, welche die Rotverschiebungen enthalten,
zu grunde gelegt.
11.5.4. Kreuzkorrelationen von Intensitäten der CMB und der Intensität der
Röntgen-Hintergrundstrahlung führen dazu, inelastische Streuungen der
CMB-Photonen
an
dem
Gravitationspotential
großräumiger
Materieverteilungen zu detektieren. Dieser sogenannte Sachs-WolfeEffekt entsteht erst nach der Rekombination, wenn sich bereits erste
Dichtekonstrate gebildet haben. Fig. 11.13 zeigt die Ergebnisse. Eine
ähnliche Kreuzkorrelation wurde vom gleichen Team zwischen CMBFluktuation und der Verteilung der Radiogalaxien gefunden.
Fig. 11.16. Kreuzkorrelaltion zwischen der Intensität des Röntgenhintergrunds
149
und der CMB-Intensität. Aus St. Boughn, R. Crittenden, Nature 427 (2004) 45.
11.6. Die Dunkle Materie.
Wir hatten bereits in den voran gegangenen Kapiteln gesehen, daß Messungen
der Gravitation etwa 7 mal soviel dunkle wie baryonische Materie ergibt. Von
der baryonischen Materie selbst wieder ist nur etwa 1/6 im Sichtbaren
leuchtende Materie in Form von Sternen oder Gas. Wir haben oben schon
gesehen, daß ein großer Teil in Form eines heißen intergalakischen Plasmas
vorliegt, das von allem durch Supernova-Ausbrüche aus den ebenen der
Spiralgalaxien in den Raum geschleudert wird und nur im Röntgengebiet
beobachtet werden kann. Die Verteilung der nichtstrahlenden baryonischen
Materie in den Galaxien und in den Haufen ist ein schwieriges Problem, an
welchen gegenwärig intensiv geforscht wird. Wir wollen hier unter dunkler
Materie nur die nichtbaryonische Form verstehen. Ihre Geschichte beginnt mit
der Feststellung von Fritz Zwicky in den 30er Jahren, daß die
Geschwindigkeitsdispersion in Galaxienhaufen so groß ist, daß leuchtende
Materie allein keinen gebundenen Zustand ergeben würde. Die nach dem
Virialsatz ermittelte Masse ist i.a. bis zu 2 Zehnerpotenzen größer als die
leuchtende Masse. Ein ähnliches Ergebnis erhält man für
Fig. 11.17. Rotationskurve der Galaxie NGC 3189. Obere Kurve verbindet Meßpunkte
(Geschwindigkeiten der Sterne als Funktion des Abstands vom Zentrum der Galaxie).
Mittlere Kurve (disk) gibt den erwarteten Verlauf wieder, wenn nur die Masse der
Scheibe beitragen würde. Untere Kurve ist der ermittelte Beitrag des Halos. Aus J.
Binney and S. Tremaine , Galactic Dynamics. Princeton University Press 1987
Galaxien (s. Fig. 11.16). Die äußeren Sterne in den Spiralarmen umlaufen die
innere Masse in kreisförmigen Bahnen wobei das Quadrat der Geschwindigkeit
proportional zur inneren Masse ist
150
υ 2 (r ) =
GM r
r
(11.34)
Mit lichtstarken Teleskopen konnten Geschwindigkeiten von weit außen
liegenden Sternen gemessen werden. Man würde erwarten, dass die
Geschwindigkeiten abnehmen, weil der Abstand zu den inneren Massen immer
größer wird. Das ist aber nicht der Fall. Was man stattdessen findet, ist eine
nahezu konstante Geschwindigkeit (s. Fig. 11.14). Daraus lässt sich die
Dichteverteilung der dunklen (nichtbaryonischen) Materie ableiten. Für die
Dichte werden verschiedene Funktionen angegeben, die alle wie ρ ∝ r − α ( α > 1 )
abklingen. Uneinig ist man sich noch über den Verlauf der Dichte im zentralen
Teil der Galaxie. Einen wichtigen Teil der Untersuchungen nehmen
Simulationsrechnungen ein.
Fig. 11.18. Hubble Funktion H(z) in Einheiten von H0 .
Sie zeigen, dass komplizierte Wechselwirkungen zwischen den entstehenden
Strukturen der Spiralgalaxien und den Halostrukturen auftreten, zwischen
welchen auch Drehimpuls ausgetauscht wird. Eine Abschätzung der Halomasse
kann mit folgender einfachen Formel erreicht werden
151
υ3circ
MH =
10GH ( z )
(11.35)
Hier ist υcirc die vom Radius unabhängige Kreisgeschwindigkeit (in Fig. 11.17
ist υcirc ≅ 150 km/s), H (z ) ist die Hubblefunktion zur Epoche z. Dabei ist
[
H ( z ) = H 0 Ω Λ + Ω M (1 + z )
3
]
1
2
(11.36)
Weil H (z ) über Ω Λ und Ω M vom kosmologischen Modell abhängig ist, hängt
auch MH davon ab. Die Masse einer Spiralgalaxie beträgt ein Bruchteil von MH ,
der in der Größenordnung von 0,05 liegt.
Diskrepanzen zwischen
Simulationen mit Λ CDM-Modellen und den
Ergebnissen der Beobachtungen werden sich durch Eingabe verbesserter
Parameter und Zunahme von verbesserten Beobachtungsdaten ausräumen
lassen. WMAP konnte auch den Beitrag leichter Neutrinos, welche gern als
„Hot Dark Matter“ beigemischt werden, auf Ω v h 2 < 0,0076 begrenzen. Zum
anderen konnte die Bildung der ersten Sterne auf etwa 200 ⋅ 10 6 Jahre vorverlegt
werden, was auch den Beginn der Reionisation festlegt, die ebenfalls Einfluss
auf die weitere Bildung (oder Verzögerung) von Strukturen nimmt.
Der große Erfolg der Λ CDM-Kosmologie ist doch, dass sie zeigt, wie in
hierarchischer Strukturbildung sich große Systeme aus kleinen gebildet haben.
Kleine Galaxien vereinigen sich und formen große Galaxien. Aber die Größe ist
begrenzt, denn das Gas in größeren Strukturen würde zur Abkühlung zu lange
brauchen, um noch größere Galaxien zu bilden. Deshalb treten größere
Strukturen nur als Cluster und Supercluster auf. Diese wieder haben sich aus
Galaxien und Galaxienhaufen aufbauen können. Heute wissen wir, dass es in
erster Linie die Halos aus dunkler Materie sind, welchen wir die im Laufe der
Zeit zunehmende Hierarchisierung, d.h. die Vereinigungen zu immer größeren
Einheiten verdanken.
Die Schwierigkeiten, Teilchen der dunklen Materie (weakly interacting massiv
particles = WIMPs), welche mit anderen Elementarteilchen wahrscheinlich nur
gravitativ wechselwirken, im Labor nachzuweisen, sind außerordentlich groß.
Dennoch werden solche Anstrengungen von Seiten der Hochenergiephysik
unternommen. WIMPs übertragen beim inelastischen Stoß mit Atomkernen
Energie. Eine Methode welche diese Energie bestimmen soll, ist der Aufbau von
Tieftemperatur-Kalorimeter.
152
Fig. 11.18. Die Halomasse bei einer Kreisgeschwindigkeit υ circ = 250 km/s
als Funktion von der Rotverschiebung
Damit hofft man Stöße von WIMPs als Temperaturerhöhung des Detektors bei
niedrigen Temperaturen (10 – 50 mK) zu messen. Die Apparaturen müssen von
radioaktiven Prozessen oder kosmischen Höhenstrahlen komplett abgeschirmt
werden. Das Experiment DAMA (Dark Matter Search) mit 100 kg NaJDetektoren ist in einem Tunnel im Gran Sasso in Italien untergebracht. Die
gemessenen Rückstoßspektren sollten sich im jahreszeitlichen Rhythmus
ändern. Tatsächlich hat man auch entsprechende Ereignisse gefunden, deren
Verifikation ist aber bisher nicht gelungen. Das amerikanische CDMS
Experiment (Cryogenic Dark Matter Search) basiert auf der Ionisationseffizienz,
ebenso das französische im Frejus-Tunnel installierte Experiment EDELWEISS
(Experience pour detecter les WIMPs en site souterrain). Das deutsche
Experiment CRESST (Cryogenic Rare Event Search with Superconducting
Thermometers) nutzt daneben auch die Messung der Szintillations-Effizienz. Da
der Wirkungsquerschnitt für die Detektion von WIMPs nicht bekannt ist, muß
man den ganzen von supersymmetrischen Theorien als möglich vohergesagten
153
Bereich untersuchen. Die dazu erforderliche Empfindlichkeit wird aber erst in
einer nächsten Generation von Experimenten erreichbar sein.
Fig. 11.19. CRESST : Installation eines SQUID-Systems am Cryostaten.
11.7. Zusammenfassung.
Es werden analytische Verfahren vorgestellt, welche es gestatten, die
Entwicklung des Dichtekontrasts mit der kosmischen Entwicklung zu verfolgen.
Wenn man davon ausgeht, dass ein Dichtekontrast von 1 nötig ist, um einen
Kollaps zu erreichen, so wird dieser mit baryonischer Materie allein bei weitem
nicht erreicht. Bei der Entwicklung der dunklen Materie setzt man voraus, dass
keine Stöße auftreten und ausschließlich gravitative Wechselwirkung auftritt.
Das Ergebnis von N-Teilchen-Simulationen im Konkordanzmodell (ΛCDM)
sind netzwerkartige Strukturen, in welchen sich baryonische Materie sammeln
kann. Galaxien sind jeweils von einem Halo aus dunkler Materie umgeben. Im
modernen Katalogen (SDSS und 2dF-Project) sind 105 – 106 Galaxien enthalten,
deren Positionen und Rotverschiebungen gemessen wurden. Ihre räumliche
Verteilung ergibt eine ähnliche Netzwerkstruktur wie die Simulationen. Die
leuchtende Materie ist nur ein kleiner Teil der baryonischen Materie. Der
größere Teil besteht aus Gaswolken ohne Sternentwicklung und heißem
intergalaktischem Gas, das bei der Entwicklung der Galaxien von Supernovae
und dem zentralen schwarzen Loch ausgeschleudert wurden.
154
11.8. Literatur
A.R.
Liddle
and
D.H.
Lyth.
Cosmological
Large Scale Structure. Cambridge Univ. Press 2000
Inflation
and
L. Guzzo : Large-Scale Structure from Galaxy to Cluster Surveys. Review in
DARK2002, 4th Heidelberg Conf. On Dark Matter in Astro- and Particle
Physics. H.-V. Klapdor-Kleingrothaus & R. Viollier eds. Springer
J. Binney and S. Tremaine, Galactic Dynamics. Princeton University Press 1987
J.R. Primack: Status of Cold Dark Matter Cosmology, astro-ph/0205391
G. Nollez: Detection of nonbaryonic dark matter: Europhysics News
July/August 2003, p. 132
Borgani, L. Guzzo : Nature 410, 169, (2001)
St. Boughn, R. Crittenden, Nature 427 (2004) 45
Max Tegmark’s Cosmological Library.
http:/www.hep.upenn.edu/~max/2df1.html
V.J. Martinez and E. Saar: Clustering Statistics in Cosmology. In SPIE
Proceedings Vol. 4847 (2002), Astronomical Data Analysis, J.-L. Stark and
Murtagh eds.
P. Anninos : Computational Cosmology. From the Early Universe to the Large
Scale Structures. http://www.livingreviews.org/Articles/Volume4/20012anninos
Astroteilchenphysik in Deutschland: Dunbkle Materie.
http://astroteilchenphysik.de/topics/dm.html
CRESST Home Page. http://wwwms.mppmu.mpg.de/cresst/
V. Springel: Die Millenium-Simulation. Sterne und Weltraum Nov. 2006, S.30 40.
155