Sterne (6)
Werbung

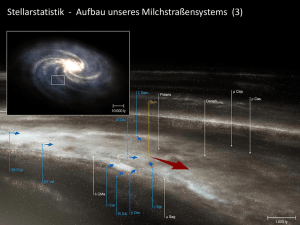
Sterne (6) Beobachtungsgrößen Welche Sternparameter können aus Beobachtungen abgeleitet werden? Beobachtungsparameter Position als Funktion der Zeit Ort in der Milchstraße Raumgeschwindigkeit (+ spektr. bestimmte Radialgeschwindigkeit) Entfernung (trigonometrische Parallaxe) Doppelstern: ungefähre Masse Helligkeit als Funktion der Zeit Bei bekannter Entfernung Leuchtkraft Lichtwechsel veränderlicher Sterne (Typisierung) Breitbandige Spektralphotometrie (Farben-Helligkeitsdiagramme) Rotationsdauer (bei Objekten mit „Sternflecken“) Farbe Effektive Temperatur (korreliert mit Farbenindex) Farben-Helligkeitsdiagramme / Hertzsprung-Russell-Diagramm Polarisation Assoziation mit intergalaktischen Staub; Magnetfelder Direkte Auflösung Interferometrie Sterndurchmesser Details in der Sternatmosphäre Masseausflüsse Sternbedeckung durch Mond Sterndurchmesser Spektroskopie Physikalisch- chemischer Aufbau der Sternatmosphäre (T, P, X) Rotation, Magnetfelder, Masseflüsse, Leuchtkraftklasse, Typ Sternseismographie Innerer Aufbau Die Bestimmung von Sternpositionen Genaue Sternpositionen benötigt man a) zur eindeutigen Identifizierung (Katalog) b) um die Eigenbewegung festzulegen c) zur Bestimmung der parallaktischen Verschiebung (Entfernung) d) um aus Abweichungen in der Eigenbewegung auf Begleiter (z.B. Exoplaneten) zu schließen Koordinatensysteme Da die Positionsbestimmung von einem Beobachtungsort erfolgt, der selbst nicht „ortsfest“ ist (rotierende kreiselnde Erde, Satellitenbahn; Erde bewegt sich um die Sonne, Sonne um das galaktische Zentrum; Galaxie um ….), ergeben sich grundlegende Probleme bei der Festlegung eines geeigneten Bezugssystems. Fundamentalastronomie Die Festlegung eines „raumfesten“ Bezugssystems ist fundamental für die Astronomie Anforderungen an ein Fundamentalsystem • Ein „fundamentales“ Koordinatensystem muß von der Bewegung der Erde (Rotation, Bahn) und von der Bewegung des Sonnensystems unabhängig sein. Der „Beobachtungsort“ Schwerpunkt Sonnensystem bleibt aber priviligiert. • Physikalisch wird es am ehesten durch ein spezielles Inertialsystem angenähert „absoluter Raum“ Newtons • Es muß praktikabel sein Drei Raumachsen – ein Bezugszeitpunkt Koordinatenursprung: Baryzentrum des Sonnensystems Ausrichtung: Rotationsachse der Erde Ein Fundamentalsystem ist ein spezielles Äquatorsystem. Da es relativ zu weit entfernten Objekten im Kosmos ruht, ist es ein Inertialsystem. Im rotierenden Äquatorsystem kann die Position eines Objektes an der Himmelskugel durch zwei Winkelmaße für einen gegebenen Zeitpunkt (Äquinoktium) eindeutig festgelegt werden: DEKLINATION REKTASZENSION Die dritte Koordinate, der Raumabstand, läßt sich z.B. über die trigonometrische Parallaxe bestimmen. Problem: Fundamentalsystem ist im Systemschwerpunkt des Sonnensystems fest verankert, der topozentrische Beobachtungsort ändert sich aber stetig relativ dazu durch die Eigenrotation der Erde und ihrer Bewegung um die Sonne. Die Richtung der Erdachse ändert sich aufgrund der Präzession / Nutation Topozentrische Örter sind ständigen Veränderungen unterworfen, die mit den wahren Änderungen der Gestirnskoordinaten (Eigenbewegung, Parallaxe) nichts zu tun haben. Diese Änderungen müssen deshalb genauestens bestimmt und bei der Reduktion topozentrischer Positionen in Abzug gebracht werden. Lösung: Man verankert das Fundamentalsystem nicht mehr mit der Erde, sondern benutzt zu deren Festlegung eine genügend große Anzahl weit entfernter „Fundamentalsterne“, deren Koordinaten und Eigenbewegung sehr genau bekannt ist – (am besten = 0). Diese Sterne werden Fundamentalsterne genannt und in Fundamentalkatalogen zusammengefaßt. Sternpositionen werden durch Relativmessungen in Bezug auf derartige Fundamentalsterne bestimmt. Heute verwendet man u.a. weit entfernte Quasare, deren Position radiointerferometrisch bestimmt wurden, als „Fundamentalsterne“ (Abbildung: ALMA-Antennen) HIPPARCOS-Mission 1989-1993 1 Million Sternörter, davon 118000 mit einer besonders hohen Genauigkeit (Winkeldurchmesser eines Golfballs in 5000 km Entfernung) Nachfolger-Mission GAIA Eigenbewegung der Sterne Die Eigenbewegung eines Sterns bezeichnet dessen Koordinaten als Funktion der Zeit in Projektion auf die Himmelskugel und stellt somit ein Abbild der relativen Raumbewegung von Erde und Stern dar. Beobachtet wird die Überlagerung von Eigenbewegung des Sterns und Erdbewegung – Bewegung des Sonnensystems Sternstrom Sterne mit hoher Eigenbewegung, die im Jahre 1880 bekannt waren… Die Eigenbewegung eines Sterns kann unsichtbare Begleiter verraten… Scheinbare astrometrische Bahn der Sonne um das Baryzentrum des Sonnensystems, beobachtet aus einer Entfernung von 10 pc Entdeckung des Sirius-Begleiters Friedrich Wilhelm Bessel 1844 „Lösung des Sirius-Rätsels“ 31. Januar 1862: Entdeckung des Siriusbegleiters durch Alvan Graham Clark.