Sterne (11) – Bestimmung von Sterndurchmessern – Teil 1
Werbung
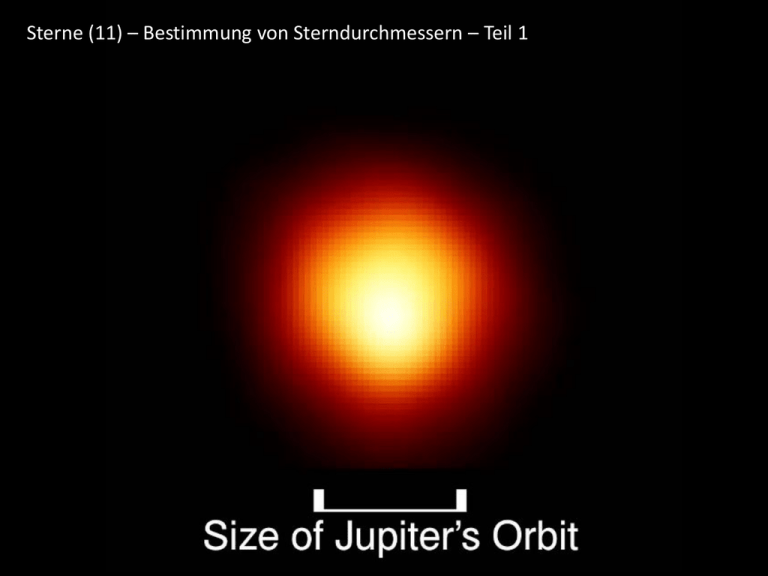
Sterne (11) – Bestimmung von Sterndurchmessern – Teil 1 Das Problem der Durchmesserbestimmung Sterne sind soweit von der Erde entfernt, daß nur einige wenige überhaupt in Riesenteleskopen als „echte“ Scheibchen (wie Planeten) abgebildet werden können. Eine Ausnahme ist die Sonne… Ein Stern mit dem Durchmesser D erscheint aus einer Entfernung r unter dem Winkel 𝛼: 𝐷 = 𝑟 tan 𝛼 ≈ 𝛼 𝑟 Ein Teleskop muß diesen Winkel auflösen können, um ein Stern als Scheibchen abzubilden. Das gelingt nur bei wenigen Sternen mit Weltraumteleskopen (Hubble) oder irdischen Teleskopen mit adaptierten Optiken. Dazu müssen die scheinbaren Sterndurchmesser größer sein als die Beugungsgrenze des Teleskops: 𝜆 𝜗 ≈ 1.22 𝑑 Auflösungsvermögen von Forschungsteleskopen Stern Beteigeuze Winkeldurchmesser 0.05“ (= 50 mas) Hubble-Aufnahme im UV 𝜗𝐻𝑢𝑏𝑏𝑙𝑒 = 0.043„ Apertur: d=2.4 m Mira (Omicron Ceti) ~ 400 Sonnendurchmesser ~ 0.6 Bogensekunden Interferometrische Bestimmung von Sterndurchmesser Fringes und Visibilität Ein Maß für die „Sichtbarkeit“ der Interferenzstreifen ist die Größe 𝑉= 𝐼𝑚𝑎𝑥 − 𝐼𝑚𝑖𝑛 𝐼𝑚𝑎𝑥 + 𝐼𝑚𝑖𝑛 I gibt dabei jeweils die Maximalhelligkeit und die Minimalhelligkeit der Interferenzstreifen an. Wird V (die Visibilität) über d aufgetragen, erhält man die Visibilitätskurve. Aus ihr läßt sich der Winkeldurchmesser des Sterns bestimmen. Rekonstruktion des Aussehens der Sternoberfläche mittels Apertursynthese Das Verfahren der Apertursynthese stammt aus der Radioastronomie. Cambridge Optical Aperture Synthesis Telescope Hochaufgelöste „Aufnahmen“ von Beteigeuze Eine „tricky“ – Methode, um Sterndurchmesser zu bestimmen Intensitätsinterferometrie nach R. Hanbury-Brown und R.Q. Twiss „Photonenstatistik“ von zeitkorrewlierten Messungen an zwei verschiedenen, durch unterschiedliche Abstände d getrennten Beobachtungsorten Korrelation der Intensitätsfluktuationen als Funktion der Basislänge d Intensitätsinterferometer von Narrabri, New South Wales Spiegeldurchmesser 6.7 Meter • Nur auf helle Sterne anwendbar (m > 2.5 Größenklassen) • Streng monochromatische Messungen (Bandbreite ~ 10 nm) • Große, aber nicht sehr genau abbildende Spiegeleleskope • SEV‘s mit sehr hoher zeitlicher Auflösung Genauigkeit (Narrabri) 1/10000 Bogensekunden ! Sterndurchmesserbestimmung mittels Speckle-Interferometrie Oftmals reicht die freie Öffnung von Riesenteleskopen (Apertur > 5 m) aus, um theoretisch Sternbildchen als „Scheibchen“ aufzulösen. Leider macht die Erdatmosphäre diesem Vorhaben einen Strich durch die Rechnung. Jedes einzelne „Speckle“-Bild stellt ein Objektbild in der beugungsbegrenzten Auflösung des Teleskops dar. Satz von monochromatischen Specklebildern eines Sterns bei einer Wellenlänge von 1500 nm Rekonstruiertes Bild von Beteigeuze Unter Einschränkungen lassen sich Speckle-interferometrische Untersuchungen zur Strukturanalyse von Atmosphären und Außenhüllen naher Riesensterne und damit zur Verifizierung von Atmosphärenmodellen einsetzen. Sternbedeckungen durch den Mond Da ein Stern eine endliche Winkelausdehnung besitzt, verschwindet er nicht plötzlich hinter dem Mondrand (nur bei hoher Zeitauflösung meßbar) Zeitlich hoch aufgelöste Lichtkurve der Bedeckung des Sterns 71 Tau (Hyaden) durch den Mond bei zwei verschiedenen Wellenlängen (450 und 700 nm)