Prof. Dr.-Ing. Herzig Vorlesung " Elektrotechnik 1"

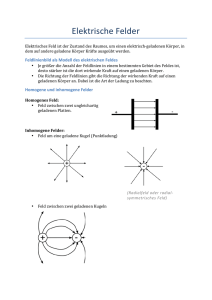
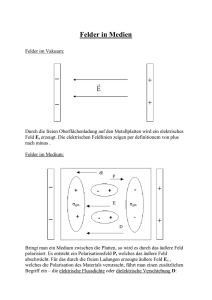
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
139
1etv41-1
4.
4.1.
4.1.1.
Elektromagnetische Felder
Grundlagen
Feldbegriff
Der Lernende kann
- die Begriffe Vektorfeld und Skalarfeld einer physikalischen Größe definieren und Beispiele angeben
- die Begriffe ebenes, parallelebenes Feld und rotationssymmetrisches Feld definieren
- das Prinzip der Darstellung der Feldgröße durch Feldlinien erläutern
- homogene und inhomogene Felder definieren
Physikalische Größen können in ihrer Umgebung einen Raumzustand verursachen,
der durch andere physikalische Größen nachgewiesen wird. In Abschnitt 2.3.3 hatten
wir festgestellt, dass jede Ladung in ihrer Umgebung den Raumzustand derart
verändert, dass auf andere Ladungen Kraftwirkungen ausgeübt werden. Einen
solchen Raumzustand bezeichnen wir als Feld. Das Feld ist somit ein bestimmter
energetischer Zustand eines Raumes. Die den Raumzustand beschreibende
physikalische Größe wird Feldgröße genannt. Ist die physikalische Größe ein Vektor
sprechen wir von einem Vektorfeld. Wird nur der Betrag der vektoriellen Feldgröße
betrachtet oder ist die physikalische Größe eine skalare Größe, sprechen wir von
einem Skalarfeld. Bei einer vektoriellen Feldgröße beschreiben Vektorfeld und
Skalarfeld gemeinsam den Raumzustand.
Ein Feld ist ein energetischer Zustand eines Raumes, bei dem die
physikalische Feldgröße in jedem Raumpunkt einen Betrag und eine Richtung
hat.
Mathematisch ist das Feld eine vektorielle und eine skalare Ortsfunktion. Ist der
Raumzustand außerdem zeitlich veränderlich, werden die Funktionen orts- und
zeitabhängig.
Beispiele:
Strömungsfeld eines Wasserflusses
Vektorfeld der gerichteten Geschwindigkeiten der strömenden Wasserteilchen
Skalarfeld der potenziellen Energie der Wasserteilchen in Fließrichtung
Gravitationsfeld der Erde
Vektorfeld der gerichteten Kraftwirkungen auf Massen
Skalarfeld der potenziellen Energien der Massen
Temperaturfeld
Vektorfeld der gerichteten Wärmeströmung in Richtung des Temperaturgefälles
Skalarfeld der Temperaturen
Ladungsfeld
Vektorfeld der gerichteten Kräfte auf geladene Teilchen
Skalarfeld der potenziellen Energie der geladenen Teilchen (Potenzial)
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
140
1etv41-1
Die Ortsfunktion der Feldgröße kann durch eine dreidimensionales
Koordinatensystem beispielsweise durch ein kartesisches Koordinatensystem mit
den Koordinaten x, y, z beschrieben werden. In praktischen Anwendungen
interessiert oft nur die Ortsfunktion der Feldgröße in einer ebenen Fläche. Wir haben
es dann mit einem ebenen Feld zu tun. Das Feld lässt sich in der Ebene vollständig
beschreiben. Ändert sich die Feldgröße senkrecht zu dieser Ebene nicht, sprechen
wir von einem parallelebenen Feld. Für die Beschreibung eines ebenen oder eines
paralleleben Feldes reicht ein zweidimensionales Koordinaten mit den kartesischen
Koordinaten x und y aus. Ist das ebene Feld rotationssymmetrisch, so sprechen wir
von einem rotationssymmetrischen Feld. Das Feld lässt sich durch eine im
Rotationspunkt beginnende Radialkoordinate beschreiben.
Die Richtungslinien des Feldvektors eines Vektorfeldes werden Feldlinien genannt,
wobei der Betrag der Feldgröße entlang der Feldlinie konstant sein kann oder sich
entlang der Feldlinie ändert. Die Gesamtheit der Feldlinien ist das Feldbild. Es ist die
grafische Darstellung der Ortsfunktion der Feldgröße. Mit den Feldlinien werden
ebene oder räumlichen Felder mathematisch modelliert. Bei der Darstellung des
Feldes durch ein Feldbild werden ausgewählte Feldlinien verwendet, dabei wird
vereinbart:
1.
Die Richtung der Feldlinien gibt in jedem Punkt des Raumes die Richtung der
Feldgröße an.
2.
Die Dichte der Feldlinien ist dem Betrag der Feldgröße proportional. Der
Abstand benachbarter Feldlinien ist daher dem Betrag der Feldgröße umgekehrt
proportional, je kleiner der Abstand, desto größer der Betrag
Verlaufen die Feldlinien in gleichem Abstand parallel, so liegt ein homogenes Feld
vor. Der Feldvektor hat in jedem Punkt des Raumes den gleichen Betrag und die
gleiche Richtung. Alle Felder, die die Homogenitätsbedingung nicht erfüllen sind
inhomogene Felder. .
Feldlinien
grafitbeschichtetes
Papier
Feldlinien
grafitbeschichtetes
Papier
G
v
G
v
MetallElektroden
MetallElektroden
Uq
Abb. 4.4.1 homogenes Feld
Abb.4.4.2 radialsymmetrisches Feld
In Abb. 4.1.1 und 4.1.2 sind ebene Felder des Geschwindigkeitsvektors bewegter
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
141
1etv41-1
Ladungen dargestellt. Auf grafitbeschichtetes Papier sind Metallelektroden aufgesetzt
und mit einer Spannungsquelle zu einem Stromkreis verbunden. In Abb. 4.1.1 liegt
ein homogenes Feld vor. Die Feldlinien des Geschwindigkeitsvektors verlaufen im
gleichen Abstand parallel, der Feldvektor ist im gesamten Feld gleich. In Abb. 4.1.2
ist ein radialsymmetrisches und damit inhomogenes Feld dargestellt. Der
Feldlinienabstand ist an der Innenelektrode kleiner als an der Außenelektrode. Die
Strömungsgeschwindigkeit nimmt von innen nach außen ab.
4.1.2.
Feldgrößen elektromagnetischer Felder
Der Lernende kann
- die Feldgrößen des elektrischen Strömungsfeldes nennen
- die Feldgrößen des elektrischen Ladungsfeldes nennen
- die Feldgrößen des Magnetfeldes nennen
- die den Materialeinfluss in den drei Feldern bestimmenden Größe angeben
Die Erscheinungen in der gesamten Elektrotechnik werden durch die elektrischen
und magnetischen Felder bestimmt. Zwischen beiden Feldern gibt es gesetzmäßige
Zusammenhänge, so dass beide Felder als elektromagnetische Felder zusammen
gefasst werden. Die Feldgrößen der elektromagnetischen Felder sind aus der
Behandlung der Gleichstromnetzwerke weitestgehend bekannt oder zusätzlich in der
Physik bereits definiert worden. Sie sollen an dieser nur zusammen gestellt werden.
Ihre detaillierte Behandlung erfolgt in späteren Abschnitten. Die den Raumzustand
beschreibenden Feldgrößen sind Feldstärke und Flussdichte. In Feldern, in denen
physikalisch keine Strömung vorhanden ist, werden aus Anschaulichkeitsgründen
ebenfalls die Begriffe Fluss und Flussdichte verwendet.
Elektrisches Feld
Elektrische Feldstärke
Stromdichte
Verschiebungsflussdichte
G
E
G
J
G
D
[E] = V/m
[J] = A/m2
[D] = As/m2
Beim elektrischen Feld muss hinsichtlich der Leitfähigkeit des Feldraumes
unterschieden werden. Für κ > 0 (leitfähiger Raum) sprechen wir vom elektrischen
G
Strömungsfeld. Hier ist die elektrische
Feldstärke
E
Ursache der Strömung, die
G
durch die Feldgröße Stromdichte J ausgedrückt wird. Die Leitfähigkeit κ des
Feldraumes bestimmt die Stromdichte:
G
G
J = κ ⋅E
(4.1.01)
Für κ = 0 sprechen wir vom elektrischen Ladungsfeld. Hier bestimmt die Ladung
G
direkt die Flussgröße, die Verschiebungsdichte D . Der Materialeinfluss des
Feldraumes wird durch die Permittivität ε beschreiben und bestimmt die elektrische
G
G D
(4.1.02)
E= .
Feldstärke:
ε
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
142
1etv41-1
Magnetisches Feld
Magnetische Feldstärke
Magnetische Flussdichte
G
H
G
B
[H] = A/m
[B] = T = Vs/m2
G
Im magnetischen Feld ist die magnetische GFeldstärke H Ursache der magnetischen
Flussgröße, der magnetischen Flussdichte B . Der Materialeinfluss des Feldraumes
wird durch die Permeabilität µ beschrieben und bestimmt die magnetische
Flussdichte:
G
G
B = µ ⋅H
(4.1.03)
Mit diesen 5 Feldgrößen lassen sich alle Erscheinungen der elektromagnetischen
Felder beschreiben, ihre Zusammenhänge untereinander und insbesondere ihr
Zeitverhalten bestimmt die Art des Feldes. Aus den vektoriellen Feldgrößen lassen
sich durch Integration skalare Feldgrößen ableiten, die deshalb auch integrale
Größen genannt werden. Im Gleichstromkreis hatten wir bereits die integralen
Größen Strom I und Spannung U kennen gelernt, die sich für das elektrische
Strömungsfeld aus Stromdichte und Feldstärke durch Integration bestimmen lassen:
G G
I = ∫ J ⋅ dA
(4.1.04)
A
G G
U = ∫ E ⋅ ds
(4.1.05)
s
Im elektrischen Ladungsfeld ergeben sich der Verschiebungsfluss Ψ aus der
Verschiebungsflussdichte und die Spannung aus der Feldstärke.
G G
Ψ = ∫ D ⋅ dA
(4.1.06)
A
G G
U = ∫ E ⋅ ds
(4.1.05)
s
Im magnetischen Feld sind die integralen Größen der magnetischen Fluss Φ und die
magnetische Spannung V.
G G
Φ = ∫ B ⋅ dA
(4.1.07)
A
G G
V = ∫ H ⋅ ds
s
(4.1.08)
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
143
1etv41-1
4.1.3.
Grundgleichungen elektromagnetischer Felder
Maxwellsche Gleichungen
Der Lernende kann
- das Induktionsgesetz angeben
- das Durchflutungsgesetz angeben
- die grundsätzliche Eigenschaft des Magnetfeldes benennen
- die grundsätzliche Eigenschaft des elektrischen Feldes bennenen
- die Materialgleichungen angeben
Felder zusammengefasst angegeben werden. In der Fachliteratur werden die
Gleichungen meist in der differenziellen Form angegeben, zu deren Behandlung
Kenntnisse in der Vektoralgebra notwendig sind. In der vorliegenden integralen Form
setzen sie nur Kenntnisse in der Vektorrechnung voraus. Verfügen Sie zurzeit noch
nicht über diese Kenntnisse, dann sollten Sie versuchen, den physikalischen Inhalt
der Beziehungen zu erfassen. Wir werden in den folgenden Abschnitten diese
Gleichungen den speziellen Aufgabenstellungen entsprechend anwendungsbereit
erarbeiten und dabei immer wieder auf diese Grundgleichungen zurück greifen.
1.
Maxwellsche Gleichung
Induktionsgesetz
G
G G
∂B G
∂ G G
∂Φ
v∫ E ⋅ ds = −∫ ∂t ⋅ dA = − ∂t ∫ B ⋅ dA = − ∂t
dΦ
dt
Der als Induktionsgesetz bezeichnete
Zusammenhang zwischen magnetischem
Feld und elektrischem Feld besagt, dass
das Linienintegral über die elektrische
Feldstärke längs eines geschlossenen
Weges (Ringintegral) gleich ist der
negativen zeitliche Änderung des mit dem
geschlossenen Weg verketteten
magnetischen
Flusses. Das Ringintegral
G G
v∫ E ⋅ ds ist der Spannungsabfall ui in einer
ui = −
geschlossenen Leiterschleife.
(4.1.09)
(4.1.10)
−
∂Φ
∂t
G
E; ui
Rechtswirbel
Abb. 4.1.3 Vorzeichenfestlegung des
Induktionsgesetzes
Er ist betragsmäßig gleich der zeitlichen Änderung des mit der Leiterschleife
verketten Flusses. Der richtungsmäßige Zusammenhang ist bei einer
Wirbelverkettung nach der Rechtsschraube positiv definiert, so dass sich ein positiver
Spannungsabfall ui, der als induzierte Spannung bezeichnet wird, bei einer negativen
Flussänderung, also bei einer zeitlichen Verkleinerung des magnetischen Flusses
ergibt.
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
144
1etv41-1
2.
Maxwellsche Gleichung
Durchflutungsgesetz
G G
G G
H
⋅
ds
=
J
∫ ⋅ dA = ∑ I
v∫
∑I = Θ
(4.1.11)
(4.1.12)
∑I
G
H
Θ = ∑I
Rechtswirbel
Abb.4.1.4 Vorzeichenfestlegung des
Durchflutungsgesetzes
Das Durchflutungsgesetz besagt, dass das Linienintegral über die magnetische
Feldstärke entlang eines geschlossenen Weges gleich der Summe der von dem
Umlauf umfassten elektrischen Ströme ist. Diese Stromsumme wird als Durchflutung
Θ bezeichnet. Ein stromdurchflossener Leiter oder ein durch eine zeitliche Änderung
des elektrischen Feldes hervorgerufener Verschiebungsstrom ist von einem
Magnetfeld umwirbelt. Ein positiver Strom erzeugt dabei einen positiven
magnetischen Feldstärkevektor im Sinne eines Rechtswirbels.
3. Maxwellsche Gleichung
Eigenschaft des Magnetfeldes
Das Hüllintegral der magnetischen Flussdichte ist gleich Null. Unter einem
Hüllintegral versteht man ein Flächenintegral über die gesamte Oberfläche eines
Volumens.
G G
B
∫ ⋅ dA = 0
Das Flächenintegral der magnetischen
Flussdichte ist nach Gleichung 4.1.07 der
magnetische Fluss. Wenn das Hüllintegral
Null ist, muss der über einen Teil der
Oberfläche eintretende magnetische Fluss
gleich dem über den Restteil der Oberfläche
austretenden Fluss sein. Die Feldlinien des
magnetischen Feldes sind in sich
geschlossene Linien. Das Magnetfeld ist
quellenfrei.
(4.1.13)
G
B
Abb.4.1.5 Feldlinien des Magnetfeldes
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
145
1etv41-1
4.
Maxwellsche Gleichung
Eigenschaft des elektrischen Feldes
Das Hüllintegral der elektrischen Verschiebungsdichte ist gleich der im Volumen
befindlichen elektrischen Ladung. Das Flächenintegral der Verschiebungsdichte ist
nach Gleichung 4.1.06 der Verschiebungsfluss.
G G
Ψ = v∫ D ⋅ dA = Q
(4.1.14)
Wenn also das Flächenintegral über die gesamte Oberfläche eines Volumens gleich
der im Volumen befindlichen Ladung ist, muss von dieser Ladung der
Verschiebungsfluss ausgehen und gleich dieser Ladung sein. Das elektrische Feld ist
ein Quellenfeld. Die Feldlinien des elektrischen Feldes beginnen an den positiven
Ladungen und enden an den negativen.
Ψ1
Q
Ψ4
Ψ = Ψ1 + Ψ 2 + Ψ 3 + Ψ 4 = Q
Ψ2
Ψ3 →
Abb.4.1.6 Ladung und Verschiebungsfluss im
Ladungsfeld
Die Beziehungen zwischen den Feldgrößen des elektrischen Strömungsfeldes, des
elektrischen Ladungsfeldes und des Magnetfeldes werden durch die stoffliche
Ausfüllung des Feldraumes bestimmt und deshalb auch Materialgleichungen
genannt. Der Materialeinfluss des Raumes wird durch diese Materialgleichungen
beschrieben. Sie geben den Zusammenhang zwischen Feld- und Flussgröße an.
D=ε⋅E
ε
Permittivität
J=κ⋅E
κ
(4.1.16)
Leitfähigkeit
B=µ⋅H
µ
(4.1.15)
Permeabilität
(4.1.17)
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
146
1etv41-1
4.1.4.
Klassifizierung der elektromagnetischen Felder
Der Lernende kann
- das elektromagnetische Feld nach seiner Zeitabhängigkeit klassifizieren
- die Eigenschaften des elektrostatischen und des magnetostatisches Feld beschreiben
- die Eigenschaft des elektrisches Strömungsfeld beschreiben
- das quasistationäre elektromagnetische Feld definieren
Aus methodischen Gründen wird das elektromagnetische Feld nicht geschlossen
behandelt sondern in einzelne Felder klassifiziert. Das Klassifizierungsmerkmal ist
dabei die Zeitabhängigkeit der Feldgrößen.
a)
Statische Felder
Das Kennzeichen der statischen Felder ist, dass keine zeitlichen Änderungen der
Feldgrößen vorhanden ist. Jegliche zeitliche Änderung d/dt = 0. Damit gibt es auch
ds
wegen v =
= 0 keine Ladungsbewegungen und damit keine elektrischen Ströme.
dt
Die Stromdichte J = 0.
Elektrostatisches Feld (Ladungsfeld)
G
G
Es wird durch die Feldgrößen E und D beschrieben. Es ist das Feld ruhender
Ladungen.
Magnetostatisches Feld
G
G
Es wird durch die Feldgrößen B und H beschrieben. Es ist das Feld ruhender
Magnete.
Zwischen den elektrischen und den magnetischen Erscheinungen gibt es keine
Verbindungen. Beide Felder sind völlig voneinander entkoppelt.
G
H
G
E
.
Abb.4.1.7 Völlige Entkopplung zwischen
elektrostatischem und magnetostatischem Feld
b)
Die Maxwellschen Gleichungen lauten für
diese beiden Felder:
G G
E
v∫ G ⋅ ds = 0
G
v∫ H ⋅ ds = 0
(4.1.18)
(4.1.19)
Stationäre Felder
Das Kennzeichen der stationären Felder sind keine zeitlichen Änderungen der
Feldgrößen. Das d/dt = 0 für alle Feldgrößen. Damit können nur zeitlich konstante
Ströme (Gleichströme) auftreten, die durch bewegte Ladungen mit konstanter
Geschwindigkeit bedingt sind. Die Stromdichte dieser Konvektionsströme JK ist
konstant. Stationäre Felder sind die elektrischen und magnetischen Felder von
Gleichströmen. Das magnetische Strömungsfeld ist ein magnetostatisches Feld,
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
147
1etv41-1
ein ruhendes Magnetfeld, das durch Gleichströme aufgebaut wird. Man spricht
deshalb beim magnetostatischem Feld allgemein vom Magnetfeld.
G
E
Durchflutungsgesetz
G
H
Abb.4.1.8 Beziehung zwischen elektrischem und
magnetischem Feld im stationären Feld
c)
Die Maxwellschen Gleichungen lauten für
das stationäre elektromagnetische Feld:
G G
E
v∫ G ⋅ ds = 0 G G
G
H
⋅
ds
= ∫ JK ⋅ dA
v∫
(4.1.20)
(4.1.21)
Quasistationäre Felder
Das Kennzeichen quasistationärer Felder ist eine mit Einschränkungen versehene
G
G
dB
dD
Zeitabhängigkeit der Feldgrößen. Es ist ein
≠ 0 und ein
≠ 0 vorhanden,
dt
dt
wobei folgende Einschränkung gilt. Geht man von periodischen zeitlichen
Änderungen der Größen aus wie sie z. B. bei zeitlich sinusförmigen Verläufen der
1
Feldgrößen mit der Periodendauer T oder der Frequenz f = vorliegt, dann muss
T
gewährleistet sein, dass T >> tL. tL ist dabei die Laufzeit der elektrischen
Erscheinung innerhalb der Schaltung oder der elektrischen Anlage. Diese Laufzeit
berechnet sich aus der maximalen Abmessung der Schaltung oder Anlage smax und
c
der Lichtgeschwindigkeit c = 300000km/s mit tL =
.
smax
Quasistationäre Felder sind Felder mit langsamen zeitlichen Änderungen der
Feldgrößen bezüglich der räumlichen Schaltungsausdehnung.
Quasistationär bedeutet dabei, dass für jeden Zeitpunkt einer Zustandsänderung die
Gesetze der stationären Felder gültig sind. Die langsame zeitliche Änderung des
elektrischen Feldes gestattet die Anwendung des Durchflutungsgesetzes nur für
Konvektionsströme und nicht für Verschiebungsströme. Der magnetische Feldaufbau
durch Verschiebungsströme bleibt unberücksichtigt. Es tritt keine Wellenausbreitung
auf. Für f = 50 Hz und damit T = 20 ms gilt die quasistationäre Betrachtungsweise mit
T = tL für Anlagengrößen mit smax = 6000 km.
Prof. Dr.-Ing. Herzig
Vorlesung " Elektrotechnik 1"
148
1etv41-1
Die Maxwellschen Gleichungen lauten
für das quasistationäre
elektromagnetische Feld:
Durchflutungsgesetz
G
H
G
E
G
G G
∂B G
v∫ E ⋅ ds = − ∫ ∂t ⋅ dA
G G
G
G
H
⋅
ds
=
J
⋅
dA
K
v∫
∫
(4.1.22)
(4.1.23)
G
∂D
∂t
G
∂B
∂t
Induktionsgesetz
Abb.4.19 Beziehung zwischen elektrischem und
magnetischem Feld im quasistationären Feld
d) Nichtstationäre Felder (Wellenfelder)
Das Kennzeichen nichtstationärer Felder ist: T < tL . Es sind Felder schnell
veränderlicher Feldgrößen. Es kommt zur Wellenausbreitung. Wellenfelder sind nicht
Gegenstand der Grundlagenausbildung Elektrotechnik. Sie werden z. B. in der
Nachrichtentechnik behandelt.
Durchflutungsgesetz
G
H
G
∂B
∂t
G
E
G
∂D
∂t
Induktionsgesetz
Abb.4.20 Beziehung zwischen elektrischem und
magnetischem Feld im Wellenfeld
Die Maxwellsche Gleichungen lauten für die
Wellenfelder:
G
G G
∂B G
(4.1.24)
v∫ E ⋅ ds = − ∫ ∂t ⋅ dA
G G
G
G
(4.1.25)
v∫ H ⋅ ds = ∫ J ⋅ dA
mit
G
G G
∂D
J = JK +
∂t
(4.1.26)