Eigenschaften der Varianz Beispiel Bootstrap Bootstrap

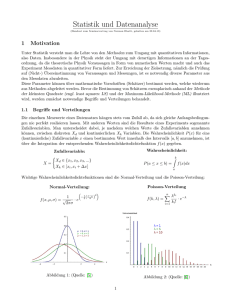
Eigenschaften der Varianz
Statistik 2
3. Vorlesung, Oktober 5, 2011
Beispiel
pˆ = X = 15%
Damit können wir Schätzer für die Wahrscheinlichkeit
grossen Differenzen von der Erwartungswert
bekommen:
P(|X-EX| ≥ ε)≤Var(X) /ε2 (Tschebischev’sche
Ungleichung)
Beispiele: Falls E=100, Standardabweichung=20,
dann P(|X-100| ≥ 40)≤400 /1600=1/4.
P(|X-100| ≥ 60)≤400 /3600=1/9.
Für unsere Schätzer: man kann die nötige
Stichprobenumfang bestimmen um eine gegebene
Genauigkeit zu erreichen.
Bootstrap
Var ( pˆ ) = p (1 − p ) / n
ˆ
Also für n=100 wir haben Var=0,001275. Ep
Daraus
=p
P (| pˆ − p |> 0,1) ≤ 0,001275 / 0,01 = 12,75%
Nicht sehr genau (aber sicher). Wir bekommen
Pünktlichere Ergebnisse, wenn wir die Verteilung unser
Schätzer auch betrachten. Für die selbe Differenz,
aufgrund der Normalverteilung:
P(| pˆ − p |> 0,1) ≈ P (| Z |> 0,1 / 0,035) = 0,5%
Bootstrap-Beispiel
Intervallschätzung
Schaetzungen aufgrund der bootstrap Stichproben
100
Die beobachtete
Wahrscheinlichkeit für
Frequency
60
40
20
Insgesamt: 1%, also ein
wenig grösser als das
Ergebnis durch die
Normalverteilung.
Die wahren Parameter der
Grundgesamtheit sind unbekannt
Antwort: aufgrund der Stichprobe
geben wir ein Schätzwert, aber es ist
nur ein Näherungswert. Wichtig: den
Fehler zu quantifizieren.
Dazu braucht man die Eigenschaften
(die Verteilung) der Schätzungen.
0
P( pˆ > 25%) = 0.8%
80
P( pˆ < 5%) = 0.2%
Falls wir können die Verteilung unser
Schätzer nicht bestimmen, können wir eine
Simulationstechnik anwenden:
Nehmen wir mehrere Stichproben aus unser
Stichprobe (mit Zurücklegen, und mit dem
selben Umfang als die originale). Wenn wir
die Schätzung für diese „Bootstrap”
Stichproben ausrechnen, bekommen wir eine
Näherung zu der Verteilung unser Schätzer .
0.05
0.10
0.15
0.20
0.25
0.30
p
1
Verteilung der Schätzer für die
Mittelwert der Normalverteilung
Vertrauensintervall
1. σ ist bekannt
Falls σ sei bekannt, wir können die Verteilung
unseren Schätzfunktion X genau bestimmen: es hat
Normalverteilung mit Parametern
(m, σ / n ). Daraus folgt, dass wir können den
Unterschied zwischen unsere Schätzung und den
wahren Parameter schätzen. Aber dessen
Eigenschaften hängen von n und σ ab, also es ist
einfacher die standardisierte Version:
Es ist nämlich standard Normalverteilt, also z.B. man
weisst, dass

P


natürlich geht es ebenso, generell für Sicherheit 1-α:

z
z
σ
σ

P m ∈  X − 1−α / 2 , X + 1−α / 2
n
n


zu benutzen.
wenn man mit vielen Stichproben die
selben m Schätzt, wird m in 100(1-α)
Prozent aller Fälle in diesen Intervall
liegen.
Korrektur für Stichproben aus endlichen
Grundgesamtheit (mit Umfang N):
z
σ
N −n
, X + 1−α / 2
N −1
n
N − n  
 = 1−α
N − 1  
Vertrauensintervall mit
Deckungswahrscheinlichkeit 1-α

t
t
σˆ
σˆ  

P m ∈  X − 1−α / 2,n−1 , X + 1−α / 2,n −1   = 1 − α
n
n 


Für n>50 die t-Quantil geht in die standard
Normalquantil über. Ebenso wenn die Verteilung der
Merkmal ist unbekannt, für n>50 kann man die
Konfidenzbereich für die Mittelwert von Punkt 1 (σ
bekannt) benutzen.
Oft wählt man der Stichprobenumfang so, dass für
gegebene Sicherheit 1-α die Intervallbreite eine
gegebene Zahl d nicht überschreitet. Dazu:
4( z1−α / 2 ) 2 σ 2
n≥
(Fall 1: σ soll bekannt sein)
2
In diesem Fall können wir die Verteilung unseren
Schätzfunktion nicht genau bestimmen, wir müssen
dazu auch noch die Varianz (und daraus die
Standardabweichung) schätzen:
n
σˆ =
2
∑(X
i =1
i
n
− X )2
σˆ =
∑ (X
i
− X )2
i =1
n −1
n −1
Die Standardisierung:
n ( X − m)
σˆ
Es ist nicht mehr standard Normalverteilt, sondern
Student (t)-verteilt.
Vertrauensintervall für die
Wahrscheinlichkeit
d

  = 1 − α

Falls σ ist nicht bekannt
Interpretation


z
σ
P m ∈  X − 1−α / 2

n



> 2  ≈ 0,05


Daraus kann man ein Vertrauensintervall
(Konfidenzintervall) für m konstruieren:
σ
σ


2σ
2σ  
P m ∈  X −
,X +
  ≈ 0,95
n
n  


n ( X − m)
n ( X − m)
In diesem Fall für die Einzelbeobachtung
(Indikatorfunktion) σ2=p(1-p), also wir
bekommen für p die folgenden Intervall (mit
Sicherheit 1-α)

z
pˆ (1 − pˆ )
z
pˆ (1 − pˆ ) 
 X − 1−α / 2

, X + 1−α / 2


n
n


k
wobei pˆ = n (die relative Häufigkeit). Um diese
Approximation gültig zu sein, brauchen wir
dass n ist gross genug (n>50).
2
Stichprobenumfang
Beispiel
Wenn aus 100 Studenten 25 die erste Prüfung
nicht bestanden haben, was kann man als
Vertrauensintervall mit α=0,05 (α=0,01) für den
Durchfallwahrscheinlichkeit geben?
Für α=0,05: 0,25-1,96*(0,25*0,75)1/2/10=0,165;
0,25+1,96*(0,25*0,75)1/2/10=0,335; Also das
Intervall lautet: (0,165;0,335)
Für α=0,01: 0,25-2,58*(0,25*0,75)1/2/10=0,138;
0,25+2,58*(0,25*0,75)1/2/10=0,362; Also das
Intervall lautet: (0,138;0,362)
Vertrauensintervall für die
Standardabweichung
Beispiel
Wieviel Studenten sollen wir fragen, um das
95%-Vertrauensintervall für den
Durchfallwahrscheinlichkeit kürzer als 0,1 zu
haben? 1,962/0,01=384 Studenten sind nötig.
Um die Länge zu halbieren braucht man 4
Mal so viel Beobachtungen.
Für die 99%-Vertrauensintervall:
2,582/0,01=666 Studenten sollen gefragt
werden.
Statistische Testverfahren
Wir haben eine Vermutung, die wir statistisch
beweisen möchten (Sachhypothese).
Formulierung dieser Aussage: es ist die
Alternativhypothese: HA (H1).
Gegenteilige Behauptung: Nullhypothese H0.
Beispiel: In diesem Jahr haben wir höheres
Monatsumsätze, als erwartet. HA: m>m0
(wobei m0 ist die Erwartung). Die
Nullhypothese (H0) lautet: m≤m0
Wieder können wir die Stichprobenumfang so
wählen, dass für gegebene Sicherheit 1-α die
Intervallbreite eine gegebene Zahl d nicht
überschreitet. Dazu:
4( z1−α / 2 ) 2 pˆ (1 − pˆ )
n≥
d2
Aber p und sein Schätzer sind unbekannt bei
der Planung der Untersuchung, so man kann
eine obere Schranke wählen:
2
z
n ≥ 1−α2/ 2
d
Voraussetzung: die Beobachtungen sind Normalverteilt.
n
Man kann es bewiesen, dass
( X − X )2
∑
i
i =1
σ2
hat ein Chi-Quadrat Verteilung mit Freiheitsgrad n-1, und
davon der Konfidenzbereich:
n

 n


 ∑ ( X i − X ) 2 ∑ ( X i − X )2  
 = 1−α
Pσ 2 ∈  i =1
, i =1
 h1−α / 2, n−1

hα / 2,n −1






wobei hα/2,n-1 und h1-α/2,n-1 sind die α/2 und 1- α/2 Quantile
der Chi-Quadrat Verteilung mit FG=n-1.
Allgemeine Testverfahren
Gleichheit („erwartete” Wert) gehört immer zur
Nullhypothese.
Antwort: aufgrund der Stichprobe berechnen wir
einen Statistik, T.
Irrtumwahrscheinlichkeit α (es soll festgelegt werden,
allgemein α=0,05 oder noch kleiner) – dazu gehört
eine kritische Schranke der Testfunktion (cα).
Mögliche Entscheidungen:
H0 ablehnen (verwerfen) – falls |T|> cα . Es ist informativ:
fast sicher, dass H0 ist nicht wahr.
H0 annehmen (beibehalten). Es bedeutet nur, dass wir
haben nicht genügend Information um es wegwerfen zu
können (also es ist gar nicht sicher, dass in diesem Fall H0
ist wahr).
3
Test für den Mittelwert der
Normalverteilung
H0: m=m0 , σ ist bekannt (z-Test)
n ( X − m0 )
ist nämlich standard normalverteilt
σ
falls H0 ist wahr.
Sei HA: m>m0 . Wir lehnen H0 ab, falls
n ( X − m0 )
Zweiseitige Alternative
Falls HA: m≠m0
wir lehnen H0 ab, falls
n | X − m0 |
σ
wobei z1-α/2 ist die 1-α/2 Quantil für die
Standard Normalverteilung (also der
kritische Region ist auch zweiseitig).
> z1−α
σ
wobei z1-α ist die 1-α Quantil für die Standard
Normalverteilung.
σ ist nicht bekannt (t-Test)
Beispiel
Wir haben die Vermutung (Alternativhypothese),
dass der tägliche Durchschnitttemperatur am
01.November hat in die letzten 25 Jahren sich
erhöht von dem früheren 7 Grad. Wir wissen,
dass die Standardabweichung beträgt 2 Grad.
Die Durchschnitt in den letzten 25 Jahren betrug
8 Grad. Können wir die Nullhypothese (m≤7) an
α=0.05 ablehnen?
Der Statistik: 5(8-7)/2=2,5.
z1-α=1,64, also
wir können HA ablehnen, der Temperatur hat
sich mit grossen Wahrscheinlichkeit erhöht.
Andere Alternativen
Falls HA: m>m0
wir lehnen H0 ab, falls
n ( X − m0 )
> t1−α ,n −1
σˆ
Falls HA: m≠m0
n | X − m0 |
> t1−α / 2 ,n −1
wir lehnen H0 ab, falls
σˆ
wobei t1-α/2,n-1 ist die 1-α/2 Quantil für die StudentVerteilung mit Freiheitsgrad n-1.
Unser Teststatistik: T = n ( X − m0 )
σˆ
wobei
∑(X − X )
n
2
i
σˆ =
i =1
n −1
es ist Student (t)-verteilt mit Freiheitsgrad n1, falls H0 ist wahr.
Sei HA: m<m0 . Wir lehnen H0 ab, falls
T<-t1-α,n-1, wobei t1-α ,n-1 ist die 1-α Quantil für
die Student-Verteilung mit Freiheitsgrad
(FG=n-1).
Eigenschaften
wobei t1-α,n-1 ist die 1-α Quantil für die StudentVerteilung mit Freiheitsgrad n-1.
> z1−α / 2
Für n>50 die t-Quantil geht in die standard
Normalquantil über. Ebenso wenn die
Verteilung der Merkmal ist unbekannt, für
n>50 kann man die z-Test für den Mittelwert
von Punkt 1 benutzen.
Oft wählt man der Stichprobenumfang so,
dass für gegebene Unterschied zwischen die
wahren m und die m0 in die Nullhypothese
der Wahrscheinlichkeit der Fehler von Typ II
nicht grösser als ein gegebenes Wert ist.
4