Statistik und Datenanalyse

Statistik und Datenanalyse
(Handout zum Seminarvortrag von Norman Bhatti, gehalten am 29.04.13)
1
Motivation
Unter Statistik versteht man die Lehre von den Methoden zum Umgang mit quantitativen Informationen,
also Daten. Insbesondere in der Physik steht der Umgang mit derartigen Informationen an der Tagesordnung, da die theoretische Physik Voraussagen in Form von numerischen Werten macht und auch das
Experiment Messdaten in quantitativer Form liefert. Zur Erreichung der Zielsetzung, nämlich die Prüfung
auf (Nicht-) Übereinstimmung von Voraussagen und Messungen, ist es notwendig diverse Parameter aus
den Messdaten abzuleiten.
Diese Parameter können über mathematische Vorschriften (Schätzer) bestimmt werden, welche wiederum
aus Methoden abgeleitet werden. Bevor die Bestimmung von Schätzern exemplarisch anhand der Methode
der kleinsten Quadrate (engl. least squares: LS) und der Maximum-Likelihood-Methode (ML) illustriert
wird, werden zunächst notwendige Begriffe und Verteilungen behandelt.
1.1
Begriffe und Verteilungen
Die einzelnen Messwerte eines Datensatzes hängen stets vom Zufall ab, da sich gleiche Anfangsbedingungen nie perfekt realisieren lassen. Mit anderen Worten sind die Resultate eines Experiments sogenannte
Zufallsvariablen. Man unterscheidet dabei, je nachdem welchen Werte die Zufallsvariablen annehmen
können, zwischen diskreten Xd und kontinuierlichen Xk Variablen. Die Wahrscheinlichkeit P (x) für eine
(kontinuierliche) Zufallsvariable x einen bestimmten Wert innerhalb des Intervalls [a, b] anzunehmen, ist
über die Integration der entsprechenden Wahrscheinlichkeitsdichtefunktion f (x) gegeben.
Wahrscheinlichkeit:
Zufallsvariable:
(
X=
Xd ∈ {x1 , x2 , x3 , ...}
Xk ∈ [xi , xi + ∆x]
P (a ≤ x ≤ b) =
Zb
f (x)dx
a
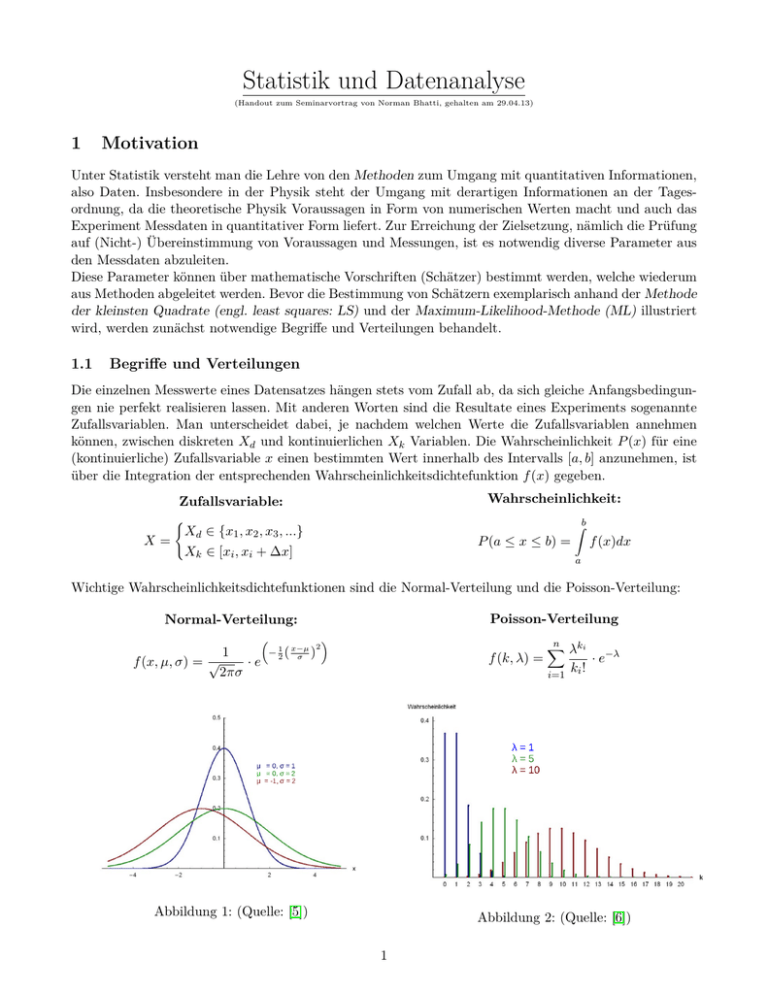
Wichtige Wahrscheinlichkeitsdichtefunktionen sind die Normal-Verteilung und die Poisson-Verteilung:
Poisson-Verteilung
Normal-Verteilung:
1
f (x, µ, σ) = √
·e
2πσ
− 21 ( x−µ
σ )
2
f (k, λ) =
n
X
λki
i=1
Abbildung 1: (Quelle: [5])
ki !
· e−λ
Abbildung 2: (Quelle: [6])
1
In Abbildung (1) ist die Normalverteilung für verschiedene Parameterwerte µ und σ abgebildet. Ein Vergleich der Kurven zeigt, dass der Erwartungswert µ ein Lagemaß darstellt, welches das Maximum der
Dichtefunktion beschreibt und dass durch die Standardabweichung σ ein Streumaß, dass die Abweichung
vom Maximum angibt, gegeben ist. Das auffälligste an der Normalverteilung ist, dass diese stets symmetrisch um den Erwartungswert µ ist.
Im Gegensatz zur Normalverteilung erkennt man auf Anhieb, dass die in Abbildung (2) dargestellten
Poissonverteilungen nicht symmetrisch um den Erwartungswert λ sind. Erst mit größer werdendem Erwartungswert und somit auch größer werdender Varianz λ = σ 2 nähert sich die Poissonverteilung einer
Normalverteilung an. Dieser Umstand ist eine Konsequenz aus dem Zentralen Grenzwertsatz und lässt
sich mit x = λ − k wie folgt angeben:
lim f (k, λ) −→ f (x, µ, σ)
λ→∞
1.2
Problemstellungen
Bei der Schätzung von Parametern, die eine Wahrscheinlichkeitsdichte charakterisieren und dementsprechend in der Lage sind Messdaten (Zufallsvariablen) zu beschreiben, durch geeignete mathematische
Formeln (Schätzer) tauchen gewisse Probleme auf. So sind zum Beispiel Datensätze oft nur Stichproben
bei denen die zugrunde liegende Verteilung meistens unbekannt ist. Ferner gibt es verschiedene Methoden,
welche einen unterschiedlichen Schätzer liefern und somit zur Bestimmung von unterschiedlichen Parametern führen können. Die Frage nach den Kriterien für einen guten Schätzer führt auf vier Anforderungen,
die ein guter Schätzer zu erfüllen hat.
2
Anforderung an gute Schätzer
Mit X̂ als Schätzwert und X0 für den wahren Wert sind die Anforderungen an einen guten Schätzer
gegeben durch:
1. Konsistenz: vergrößert man zunehmend den Datensatz (Informationsmenge) aus dem X̂ geschätzt
wurde, so sollte im Grenzübergang lim X̂ = X0 der geschätzte Wert dem wahren Wert entsprechen.
n→∞
2. Erwartungstreue: der Erwartungswert von Schätzwerten, die mit demselben Schätzer aus verschiedenen Datensätzen ermittelt wurden, sollte dem wahren Wert entsprechen (E[X̂] = X0 ).
3. Effektivität: die Varianz V (X̂) des ermittelten Schätzwertes sollte möglichst klein sein.
4. Robustheit: würde man falsche Daten/Voraussetzungen (z.B. bedingt durch eine schlechte Messung) einer Schätzung zu Grunde legen, so sollte dies bei einem guten Schätzer keinen großen Einfluss
auf die vorgenannten Eigenschaften (Konsistenz, Erwartungstreue & Effektivität) haben.
3
Methoden die zu guten Schätzern führen
1. Die Methode der kleinsten Quadrate (engl. least squares: LS)
(Für symmetrische Verteilungen: Konsistent, Erwartungstreu und Effizient)
2. Die Maximum-Likelihood-Methode (ML)
(Konsistent, asymptotische Erwartungstreue und Effizienz)
2
3.1
Die Methode der kleinsten Quadrate (LS)
Wenn durch yi die Messwerte mit jeweiligen Fehler σi geben sind und durch f (xi , a) eine von einem oder
mehreren Parametern (gekennzeichnet durch a) abhängige Modellfunktion beschrieben wird, dann gilt:
n
P
(yi −f (xi ,a))2
• Berechne die Summe: s =
σi2
i=1
• Minimiere die Summe:
3.2
ds
da
= −2 ·
(Summe der Abweichungsquadrate)
n
P
yi −f (xi ,a)
σi2
i=1
·
df (xi ,a)
da
=0
Die Maximum-Likelihood-Methode (ML)
Hat man einen Datensatz mit n Werten und ist die zugrunde liegende Wahrscheinlichkeitsdichte bekannt,
dann kann man einen oder mehrere Parameter (gekennzeichnet durch a) über die ML-Methode bestimmen,
indem man wie folgt vorgeht:
• Bilde und maximiere L(a) =
n
Q
f (xi | a) (Likelihood-Funktion)
i=1
n
P
• Alternativ: Minimiere F (a) = −
ln(f (xi | a))
i=1
(Log-Funktion ist stetig und monoton ⇒ Maximum an derselben Stelle)
Dabei beschreibt die Likelihood-Funktion das Produkt der Wahrscheinlichkeitsdichten, die sich für jeden
Messwert bei festem Parameter ergeben.
3.3
Beispiel: Geradenanpassung zur Illustration von LS und ML
M e th o d e d e r k le in s te n Q u a d ra te
M a x im u m -L ik e lih o o d -M e th o d e
7
7
6
6
λ4= y 4 = 5 , 4
r4
5
5
λ3= y 3 = 4 , 3
R e s id u e n
y
4
λ 2= y 2 = 3 , 2
4
y
3
r3
r2
λ1= y 1 = 2 , 1
2
3
1
2
r1
3
4
5
6
7
8
9
x
1
3
4
5
6
7
8
9
x
Es müssen die Residuen ri (Abweichungen zwischen Messdaten und Modellfunktion) bestimmt
werden. Anschließen wird gemäß (3.1) vorgegangen:
s =
=
4
X
(yi − f (xi , a1 , a2 ))2
i=1
4
X
i=1
σi2
ri2
σ2
, mit σi ≡ σ
(Minimiere die Summe s)
Es wurden dieselben poissonverteilten Messdaten wie
bei der LS-Methode zugrunde gelegt. Zur Bestimmung
und Maximierung der Likelihood-Funktion:
L(a1 , a2 ) =
4
Y
f (xi | a1 , a2 )
i=1
ist es zunächst notwendig für jeden Messwert xi den
y-Wert, den die Gerade, erzeugt durch die Parameter
a1 und a2 annimmt, zu bestimmen und diesen mit dem
Parameter λ der zugrunde liegenden Poissonverteilung
zu identifizieren. Die entsprechende Wahrscheinlichkeitsdichten werden für die jeweiligen Parameter λi
bestimmt und in L(a1 , a2 ) berücksichtigt.
3
3.4
Beispiel: Simulation zur Illustration von LS und ML
Bei der Geradenanpassung im vorangegangenen Beispiel würde man sowohl durch die LS-Methode, als
auch mit der ML-Methode Resultate für die Parameter a1 und a2 erhalten. Die Frage, die sich dabei
natürlich stellt, ist welche der beiden Methoden die besseren Resultate liefern würde. Um diese Frage zu
beantworten wird der folgende β − Zerfall simuliert:
11
11
β−
Be −−−−−−−→
B
λ=0,050s−1
und an den simulierten Daten eine Exponentialfunktion mit Hilfe der LS- und ML-Methode angepasst.
Die Funktionsweise der Simulation und der Anpassung kann über das folgende Fließschema nachvollzogen
werden.
Wahrer Kurvenverlauf
N(t) = N0 * exp(-λ*t)
(Gebe Parameter: N0 & λ vor)
1
Zufallsgenerator
1
Werte für t
(Poisson-Verteilung)
Berechne N(t)
2
2
LS
ML
- Berechne Fehler: sqrt(N(t))
- Berechne neg. Log-Likelihood-Fkt.: F(x,N0,λ)
- Berechne Hessematrix (Fehler auf Schätzwert)
3
- Setze Fehler für N(t)=0 auf 1
- Bestimme: Summe der Residuen-Quadrate
- Minimiere F(x,N0,λ) → Schätzer
- Minimiere Summe → Schätzer
3
3
3
Diagramm
Die unten abgebildete Diagramme geben die Resultate der Simulation/Fit für die vorgegebenen Parameter λs = 0, 050s−1 und Ns = 100 bzw. Ns = 10 wieder. Die einzelnen Kurven lassen sich über die Farbe,
gemäß den Angaben im Fließschema, den jeweiligen Methoden zuordnen.
R a d io a k tiv e r Z e rfa ll v o n
1 2 0
1 1
B e ( N s= 1 0 0 )
R a d io a k tiv e r Z e rfa ll v o n
1 1
B e ( N s= 1 0 )
1 2
1 0 0
N s = 1 0 0 ; λs = 0 , 0 5 0
N
L S
8 0
M L
N
= ( 9 9 , 5 1 + / - 5 , 2 4 ) ; λM L = ( 0 , 0 4 9 5 + / - 0 , 0 0 2 6 )
6 0
4 0
L S
N
8
N (t) [Im p ]
N (t) [Im p ]
N
N s = 1 0 ; λs = 0 , 0 5 0
1 0
= ( 9 9 , 0 0 + / - 3 , 4 1 ) ; λL S = ( 0 , 0 5 0 6 + / - 0 , 0 0 1 7 )
= ( 8 , 1 6 + / - 1 , 1 2 ) ; λL S = ( 0 , 0 5 5 3 + / - 0 , 0 0 7 7 )
M L
= ( 1 0 , 0 3 + / - 1 , 6 8 ) ; λM L = ( 0 , 0 5 1 1 + / - 0 , 0 0 8 5 )
6
4
2 0
2
0
0
0
1 0
2 0
3 0
4 0
0
5 0
1 0
2 0
3 0
4 0
5 0
t [s]
t [s]
Fit Ergebnisse
Ns [Imp]
10
100
λs [1/s]
0,050
0,050
λM L [1/s]
(0, 0511 ± 0, 0085)
(0, 0495 ± 0, 0026)
λLS [1/s]
(0, 0553 ± 0, 0077)
(0, 0506 ± 0, 0017)
Man kann in dem Diagramm für Ns = 100 keinen nennenswerten Unterschied zwischen den einzelnen
Kurven ausmachen und auch die ermittelten Werte für den Fitparameter λ aus der LS-Methode und der
ML-Methode lassen sich unter Berücksichtigung der Fehler mit der Simulations-Vorgabe λs = 0, 050s−1
4
vereinbaren. Bei einer Vorgabe von Ns = 10 kann man hingegen einen klaren Unterschied zwischen den
beiden Methoden ausmachen. So erhält man durch die LS-Methode einen signifikant größeren Wert für
die Zerfallskonstante λ, während bei der ML-Methode das Resultat immer noch sehr nahe an der Vorgabe
liegt. Die Ursache für diesen Unterschied lässt sich darauf zurückführen, dass für Ns = 10 nicht nur viele
Nullraten vorkommen, sondern auch die zugrunde liegende Verteilung asymmetrisch ist. Erst für größer
werdende Ns -Werte geht die Poissonverteilung in eine symmetrische Normalverteilung über und es lässt
sich kein nennenswerter Unterschied zwischen den beiden Methoden ausmachen. Man kann sich diesen
Umstand auch anhand des nachfolgenden Rechenbeispiels vor Augen führen.
3.5
Rechenbeispiel zur Illustration von LS und ML
Die Aufgabenstellung sei es den Parameter µ der (symmetrischen) Normalverteilung zu schätzen. Zu diesem Zweck ermittle man mit der ML- und der LS-Methode die jeweiligen Schätzer.
(1) Ermittle den Schätzer aus ML:
F (µ) = −
n
X
ln (f (xi | µ)) = −
i=1
n
X
i=1
n
X
dF (µ)
xi − µ !
=−
=0
dµ
σ2
i=1
1
ln √
−
2πσ 2
=⇒
µ=
1
2
xi − µ
σ
2
n
1X
xi
n i=1 σ
(2) Ermittle den Schätzer aus LS:
χ2 =
n
X
(yi − f (xi , µ))2
i=1
n
X
σi2
,
mit f (xi , µ) ≡ µ , σi ≡ σ
yi − f (xi , µ) df (xi , µ) !
dχ2
= −2
·
=0
dµ
dµ
σi2
i=1
=⇒
n
yi
1X
µ=
n i=1 σ
Ein Vergleich der ermittelten Schätzer führt zu dem wichtigen Resultat, dass die ML-Methode die LSMehtode als Spezialfall für symmetrische Verteilungen enthält.
4
Zusammenfassung und Fazit
Abschließend kann man sagen, dass es keine allgemeingültigen Methoden gibt, um (gute) Schätzer zu
bestimmen. Während die LS-Methode ausschließlich für symmetrische Verteilungen (Normal-, Gleichverteilung) mit geringem Rechenaufwand zu guten Schätzern führt, kann man bei der ML-Methode verschiedene Verteilungen berücksichtigen. Insbesondere eignet sich die ML-Methode somit auch für Experimente
mit geringen Zählraten. Als Nachteil der ML-Methode muss man jedoch den sehr hohen Rechenaufwand
und die a priori Kenntnis über die zugrunde liegende Verteilung anführen. Die ML kann als eine Verallgemeinerung der LS aufgefasst werden, da sie Diese als Spezialfall enthält.
Literatur
[*]
Notiz: Diagramme/Grafiken/Tabellen ohne Verweise auf die nachfolgenden Quellen wurden von dem Redner selbst angefertigt.
[1]
V.Blobel, Statistische und numerische Methoden der Datenanalyse, Teubner, 1998
[2]
S.Brandt, Datenanalyse, BI-Wissenschaftsverlag, 1992
[3]
G.Cowan, Statistical Data Analysis, Oxford University Press, 1998
[4]
http://www.students.uni-mainz.de/wiebe/work/statistik/statistik.pdf
(Modified: Fr 02 Dez 2005 17:04:07 CET)
[5]
http://de.wikipedia.org/wiki/Normalverteilung
(Modified: So 12 Mai 2013 20:08:31 CEST)
[6]
http://de.wikipedia.org/wiki/Poisson-Verteilung
(Modified: Mi 08 Mai 2013 19:04:03 CEST)
5