2. Nullstellensuche - Umwelt

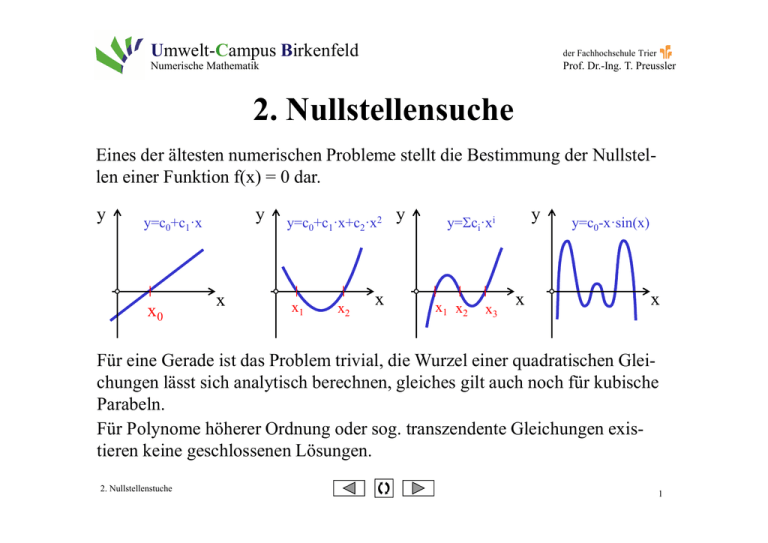
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
2. Nullstellensuche
Eines der ältesten numerischen Probleme stellt die Bestimmung der Nullstellen einer Funktion f(x) = 0 dar.
y
y
y=c0+c1·x
x0
x
y=c0+c1·x+c2·x2
x1
x2
x
y
y
y=Σci·xi
x1 x2
x3
x
y=c0-x·sin(x)
x
Für eine Gerade ist das Problem trivial, die Wurzel einer quadratischen Gleichungen lässt sich analytisch berechnen, gleiches gilt auch noch für kubische
Parabeln.
Für Polynome höherer Ordnung oder sog. transzendente Gleichungen existieren keine geschlossenen Lösungen.
2. Nullstellenstuche
1
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
2.1 Intervallschachtellung
Das einfachste Verfahren zur Nullstellenbestimmung stellt das Intervallschachtellungsverfahren (Bisektion) dar. Es liefert für ein Intervall [a,b] die
Lösung von f(x) = 0, wenn die Funktion im Intervall stetig ist und die Funktionswerte f(a) und f(b) entgegen gesetzte Vorzeichen besitzen.
Zu Beginn der Approximation wird a1= a und b1= b gesetzt und der Mittelpunkt des Intervalls [a1, b1] berechnet.
x1 = a1 +
b1 − a1
2
Ist f(x1) = 0, ist die Nullstelle mit x0= x1 im Intervall gefunden.
Wenn nicht, wird geprüft, ob die Funktionswerte f(a1) und f(x1) ungleiche
Vorzeichen haben. Dann liegt die gesucht Nullstelle im Intervall [a1, x1].
Andernfalls liegt die Nullstelle im Intervall [x1, b1].
Das Verfahren wird so lange fortgesetzt, bis die Nullstelle x0 hinreichend
genau durch die Näherung xn approximiert wird.
2. Nullstellenstuche
2
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
IntervallSchachtellungsverfahren:
y
y=f(x)
f(b1)
f(x1)
a1=a
x2
x
x3
f(a1)
x1
b1=b
f(x2)
Ein Intervall [ai+1, bi+1], das eine Nullstelle der Funktion f(x) enthält, wird aus
einem Intervall [ai, bi], konstruiert mit
xi +1 = ai +
bi − ai
2
Dann gilt ai+1= ai und bi+1= xi , wenn f(ai)·f(xi) < 0 ist, andernfalls wird ai+1= xi
und bi+1= bi gesetzt.
2. Nullstellenstuche
3
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Die Approximation wird nach n Schritten abgebrochen, wenn die Länge des
Intervalls [an, bn] kleiner ist als ein vorgegebener Toleranzwert Tol
an − bn < Tol
Vor Beginn der Bisektion muss ein Intervall [a, b] gefunden werden, für das
f(a)·f(b) < 0 zutrifft. Bei jedem Iterationsschritt n wird die Intervalllänge
halbiert. Daraus folgt mit
n
1
  ⋅ (b − a ) = xn − xn −1 < Tol
2
die Anzahl der benötigten Schritte n für eine vorgegebene Toleranz
b−a
b−a
n > log 2 
 ≈ 1,443 ⋅ ln

 Tol 
 Tol 
mit dem natürlichen Logarithmus. Die Anzahl der Iterationen ist bei vorgegebener Genauigkeit abhängig von der Länge des Startintervalls.
2. Nullstellenstuche
4
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Vorteile des Intervallschachtellungsverfahrens:
• Es führt theoretisch immer zu einer Lösung
• Die für eine vorgegebene Genauigkeit notwendige Anzahl von Schritten
kann vorab berechnet werden
Nachteile:
• Es konvergiert langsam (eine Binärstelle je Iterationsschritt)
• Gute Näherungen können im Verlauf der Iteration wieder verloren gehen
Es wird daher oft als zuverlässige Startroutine für effizientere Verfahren benutzt.
Obwohl das Verfahren grundsätzlich konvergiert, sollte in einer Anwendung
eine max. zulässige Anzahl von Iterationsschritten definiert werden, da es bei
kleinen Intervalllängen aufgrund von Rundungsfehlern zu Endlosschleifen
kommen kann. Weiterhin ist zu prüfen, ob der Mittelpunkt eines Intervalls
bereits die gesuchte Nullstelle darstellt.
2. Nullstellenstuche
5
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Beispiel: y = x3 – 4x2 – 11x + 30 = 0
Startintervall:
Nullstellen: x1=-3; x2=2; x3=5;
Genauigkeit:
Anzahl der n > log  b − a  ≈ 1,443 ⋅ ln 3 − 0  ≈ 8,2
2
Iterationen:
 Tol 
 0,01 
y = x3 – 4x2 – 11x + 30 = 0
xi
0.01
Start
ai
bi
1
0,000
3,000
1,500 7,875 30,000 -12,000 a2 = x1
2
1,500
3,000
2,250 -3,609 7,875 -12,000 b3 = x2
3
1,500
2,250
1,875 1,904 7,875
-3,609 a4 = x3
4
1,875
2,250
2,063 -0,929 1,904
-3,609 a4 = x3
...
...
...
8
1,993
2,016
2,004 -0,060 0,113
-0,239 b9 = x8
9
1,993
2,004
1,998 0,015
-0,060
...
f(ai)
3
i
...
f(xi)
0
...
0,113
f(bi)
...
Bem.
...
Nach 9 Iterationsschritten wird mit x8-x9 = 2,004-1,998 = 0,006 < Tol die erforderliche Genauigkeit erreicht.
2. Nullstellenstuche
6
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Flussdiagramm
Intervallschachtellung
Start
Deklarationen
a, b, Tol, max
ja
f(a)*f(b)>0
nein
Nullstelle nicht
im Intervall
Mittelpunkt
x=a+(b-a)/2
ja
f(x)=0
nein
f(x)*f(a)<0
nein
a=x
ja
b=x
ja
b-a<Tol
ja
Nullstelle ist
Mittelpunkt
Nullstelle
gefunden
nein
i<max
nein
Keine
Konvergenz
Stop
2. Nullstellenstuche
7
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Sub Bisektion( )
'Nullstellensuche nach dem Intervallschachtellungsverfahren
'Autor: T. Preussler
'Deklarationen
Dim a, b, Tol, x, dx
Dim i, max
'Genauigkeit
Tol = Val(Slide20.txtTol.Value)
max = 1000
'Startintervall
a = Val(Slide20.txta.Value)
'Anfangswert
b = Val(Slide20.txtb.Value)
'Endwert
If y(a) * y(b) > 0 Then
MsgBox "Keine oder mehrere Nullstelle im Intervall"
Exit Sub
End If
'Schleife
For i = 1 To max
x = a + (b - a) / 2
'Mittelpunkt
'Nullstelle ist Mittelpunkt
If y(x) = 0 Then
Text = "Die Nullstelle ist Mittelpunkt" + Str(x)
MsgBox Text
Exit Sub
End If
2. Nullstellenstuche
'Auswahl des Suchintervalls
If y(x) * y(a) < 0 Then
b=x
Else
a=x
End If
'Nullstelle gefunden
If Abs(b - a )< Tol Then
Text = "Die Nullstelle wird nach " + Str(i) + " Schritten
mit " + Str(x) + " ermittelt"
MsgBox Text
Exit Sub
Else
Text = "i =" + Str(i) + " x =" + Str(x)
MsgBox Text
End If
Next i
MsgBox "Keine Konvergenz"
End Sub
Function y(x)
'Funktionswert einer kub. Parabel
y = 30 - 11 * x - 4 * x ^ 2 + x ^ 3
End Function
8
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
2.2 Sekantenverfahren
Beim Sekantenverfahren geht man ebenfalls von einem Startintervall [a, b]
aus und setzt x0= a und x1= b. Durch die Punkte P0(x0, f(x0)) und P1(x1, f(x1))
der Funktion f(x) wird eine Gerade konstruiert. Der Schnittpunkt x2 dieser
Sekante mit der x-Achse stellt die erste Näherung der gesuchten Nullstelle
dar.
Im nächsten Schritt wird die Sekante durch die Punkte P1(x1, f(x1)) und
P2(x2, f(x2)) gelegt und der Schnittpunkt x3 mit der x-Achse als verbesserte
Näherung der Nullstelle berechnet.
Das Verfahren wird so lange fortgesetzt, bis die Nullstelle hinreichend genau
durch die Näherung xn approximiert wird.
Im allgemeinen liegt beim Sekantenverfahren der Schnittpunkt der Sekante
mit der x-Achse näher an der gesuchten Nullstelle als beim Intervallschachtellungsverfahren und konvergiert daher besser.
2. Nullstellenstuche
9
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Sekantenverfahren:
y
f(x1)
x0=a
x2
x3 x5
x4
f(x4)
x1=b
x
f(x3)
f(x2)
f(x0)
y=f(x)
Kennzeichen des Verfahrens ist, dass die Sekanten immer mit den direkt auf
einander folgenden Punkten Pi und Pi+1 gebildet werden, wobei ein Intervall
die Nullstelle notwendigerweise nicht enthalten muss.
2. Nullstellenstuche
10
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Ausgehend von einem Startintervall [a, b] wird x0= a und x1= b gesetzt. Mit
der Geradengleichung (y-y1)/(x-x1) = (y1-y0)/(x1-x0) durch die Punkte P0 und
P1 folgt die Gleichung der Sekante
y = f ( x1 ) +
f ( x1 ) − f ( x0 )
⋅ ( x − x1 )
( x1 − x0 )
Den Schnittpunkt der Sekante mit der x-Achse erhält man aus
0 = f ( x1 ) +
f ( x1 ) − f ( x0 )
⋅ ( x2 − x1 )
( x1 − x0 )
und nach x2 aufgelöst
x2 = x1 −
f ( x1 ) ⋅ ( x1 − x0 )
f ( x1 ) − f ( x0 )
ergibt sich die erste Näherung der Nullstelle und damit die allgemeine Berechnungsvorschrift für das Sekantenverfahren:
2. Nullstellenstuche
11
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Die Approximation xi+1 einer Nullstelle der Funktion f(x) ergibt sich mit den
Näherungen xi und xi-1 nach der Gleichung
xi +1 = xi −
f ( xi ) ⋅ ( xi − xi −1 )
f ( xi ) − f ( xi −1 )
Das Startintervall muss beim Sekantenverfahren nicht die Nullstelle enthalten.
y
y
f(x2)
f(x )
f(x )
1
2
x4
x0=a
x1=b x3
f(x1)
f(x0)
y=f(x)
x0=a
f(x3)
x2
x
x2
x1=b
x
f(x0)
y=f(x)
Allerdings konvergiert das Sekantenverfahren nicht immer. Bei Konvergenz
ist das Verfahren jedoch wesentlich schneller als die Intervallschachtellung.
2. Nullstellenstuche
12
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Auch beim Sekantenverfahren wird die Approximation abgebrochen, wenn
die Länge des Intervalls die vorgegebene Genauigkeit erreicht hat.
Startintervall:
Genauigkeit:
Beispiele: y=x^3–4x^2–11x+30=0
-4
4
0.01
Start
60
40
i
xi-1
xi
f(xi-1)
f(xi)
xi+1
20
1
0
3,000
30,000
-12,000
2,143
2
3
2,143
-12
-2,099
1,961
3
2,143
1,961
-2,099
0,586
2,001
4
1,961
2,001
0,586
-0,011
2,000
y
0
-4
-2
0
2
4
6
-20
-40
-60
x
Gegenüber der Intervallschachtellung kommt man beim Sekantenverfahren
mit ca. der Hälfte der Iterationsschritte aus.
2. Nullstellenstuche
13
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
2.3 Newton´sches Verfahren
Bei den bisher behandelten Verfahren werden die Nullstelle einer Funktion
berechnet durch Geraden, die den Verlauf der Kurve f(x) approximieren.
Die beste Näherung einer Funktion durch eine Gerade stellt die Tangente in
einem Punkt der Kurve dar. Das Newtonsche Verfahren verwendet daher zur
Nullstellenbestimmung Tangenten der Funktion.
Vorausgesetzt, die Funktion f(x) ist in der Umgebung einer Startnäherung x1
der Nullstelle differenzierbar, erhält man die Gleichung der Tangente durch
y = f ( x1 ) + f ' ( x1 ) ⋅ ( x − x1 )
mit der Ableitung f´(x) der Funktion f(x). Nullsetzen und auflösen liefert
eine verbesserte Näherung der gesuchten Nullstelle
x2 = x1 −
mit f´(x1) ≠ 0.
2. Nullstellenstuche
f ( x1 )
f ' ( x1 )
14
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Newtonsche
Verfahren:
y
f(x2)
y=f(x)
f(x4)
x1 x3
x4
x5
f(x1)
x2
x
f(x3)
Die Approximation xi+1 einer Nullstelle der Funktion f(x) errechnet sich aus
der Näherung xi mit
xi +1 = xi −
f ( xi )
f ' ( xi )
Das Verfahren konvergiert nur, wenn f´(xi) ≠ 0 ist. Wenn es konvergiert, dann
jedoch wesentlich schneller als die anderen Verfahren.
2. Nullstellenstuche
15
Umwelt-Campus Birkenfeld
der Fachhochschule Trier
Numerische Mathematik
Prof. Dr.-Ing. T. Preussler
Man kann zeigen, das sich im Idealfall mit jedem Schritt die Anzahl der
signifikanten Stellen verdoppelt, d. h. die Genauigkeit wächst quadratisch!
Nachteilig beim Newtonschen Verfahren ist aber, dass neben der Funktion
f(x) auch deren erste Ableitung f´(x) bekannt sein muss.
Startnäherung:
Genauigkeit:
Beispiel:
y = x3 – 4x2 – 11x + 30 = 0
Ableitung: y´ = 3x2 – 8x – 11
Nullstellen: x1=-3; x2=2; x3=5;
y = x3 – 4x2 – 11x + 30 = 0
2. Nullstellenstuche
7
0.001
Start
i
xi
f(xi)
f´(xi)
xi+1
1
0
30,000
-11,000
2,727
2
2,727
-9,467
-10,504
1,826
3
1,826
2,665
-15,605
1,997
4
1,997
0,048
-15,013
2,000
16